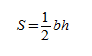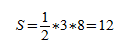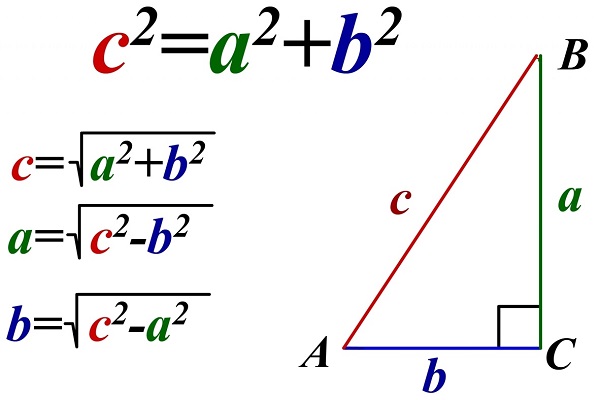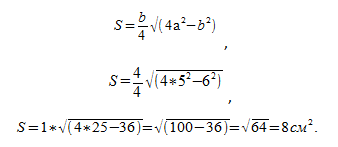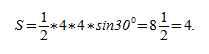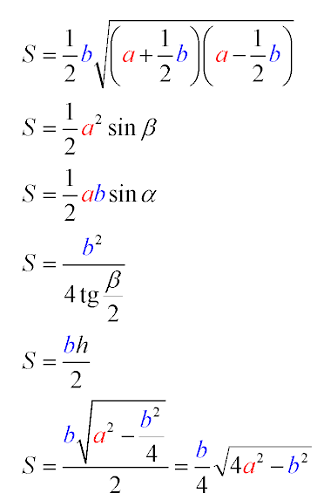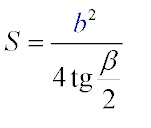Как найти площадь треугольника если известно тангенс - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

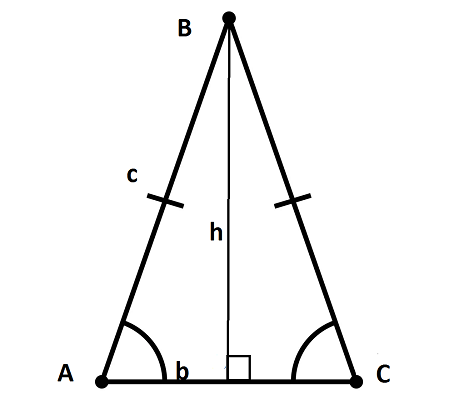
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
Поделите все на 4.

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

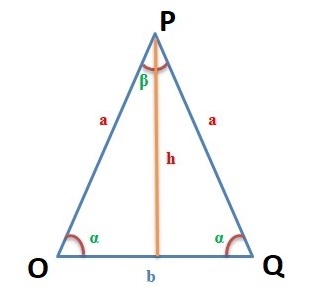
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

Найдите периметр. Для этого сложите все три стороны.
Найдите полупериметр – разделите периметр на два. Запомните значение.
Отнимите от полупериметра длину первой стороны. Запомните.
Отнимите от полупериметра длину второй стороны. Тоже запомните.
Отнимите от полупериметра длину третьей стороны. И ее запомните.
Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Площадь равнобедренного треугольника — формулы вычисления

Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.

Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.

Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;

через угол между двумя сторонами и величину одной из них;

по двум сторонам;

через синус противолежащего основанию угла;

зная синус прилежащего угла и др.

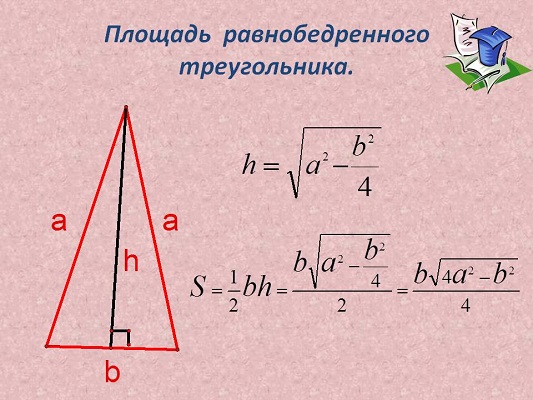
Площадь равнобедренного треугольника через высоту

Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.

У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.

И общая их площадь сводится к:

b — размер основания;

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.

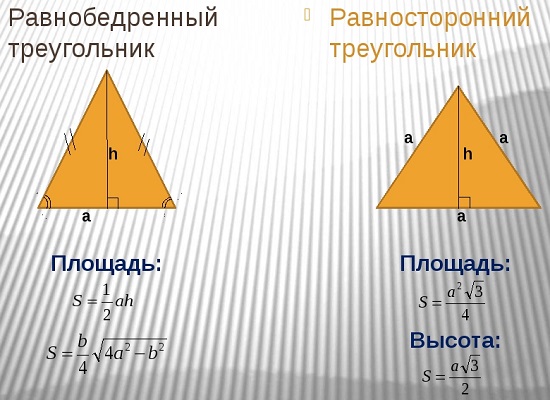
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

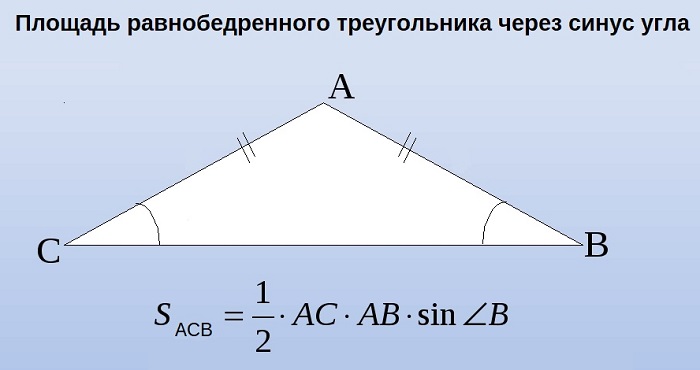
Площадь равнобедренного треугольника через синус угла

В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.

В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Формула площади равнобедренного треугольника через тангенс угла

Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.

Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90 0 — угол OPQ.

SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2

Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

источники:

http://sprint-olympic.ru/uroki/geometrija/85090-ploshad-ravnobedrennogo-treygolnika-formyly-vychisleniia.html

http://mozgan.ru/Geometry/AreaTriangle

Источник

В этой статье собраны наиболее популярные формулы для нахождения площади треугольника.

Как найти площадь треугольника по высоте?

Если известно основание и высота, проведенная к основанию треугольника, можно вычислить площадь треугольника.

(S=frac{1}{2}a*h)

Калькулятор площади треугольника по высоте и основанию

Основание треугольника:

Высота треугольника:

Как найти площадь треугольника: формула Герона

Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры:

Треугольник

(S=sqrt{p(p-a)(p-b)(p-c)})

где (a,b,c) – стороны треугольника, (p=frac{a+b+c}{2}) – его полупериметр.

Калькулятор площади треугольника по трем сторонам

Первая сторона треугольника:

Вторая сторона треугольника:

Третья сторона треугольника:

Формула нахождения площади треугольника по окружности

Как вычислить площадь треугольника, если известна окружность и три его стороны?

Как узнать площадь треугольника по окружности

(S=frac{a*b*c}{4R})

Калькулятор площади треугольника по трем сторонам и радиусу описанной окружности

Первая сторона треугольника:

Вторая сторона треугольника:

Третья сторона треугольника:

Радиус описанной окружности R:

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника, необходимо знать длины двух катетов. После этого можно воспользоваться формулой:

S = (a * b) / 2

, где a и b — длины катетов. Просто перемножьте значения длин катетов и разделите результат на два, чтобы найти площадь прямоугольного треугольника.

Как узнать площадь треугольника по радиусу и полупериметру

Можно найти площадь треугольника, когда мы знаем полупериметр и радиус вписанной окружности:

Площадь треугольника: формулы по вписанной окружности

(S=pr)

где r — радиус вписанной окружности, (p=frac{a+b+c}{2})– его полупериметр.

Калькулятор площади треугольника по трем сторонам и радиусу вписанной окружности

Первая сторона треугольника:

Вторая сторона треугольника:

Третья сторона треугольника:

Радиус вписанной окружности R:

Как найти площадь треугольника по стороне и тангенсу: формула

Формула нахождения площади по стороне и тангенсу углов треугольника:

S треугольника

(S=frac{c^2}{2(ctgA+ctgB)})

Основные формулы площади треугольника для учащихся 5-6 классов

Для ученика 5-6 класса обычно достаточно знать две формулы для вычисления площади треугольника:

Формула площади произвольного треугольника по основанию и высоте:

S = (a * h) / 2

где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника, опущенная на это основание.
Формула Герона:

S = sqrt(p * (p — a) * (p — b) * (p — c))

где S — площадь треугольника, a, b, c — длины сторон треугольника, p — полупериметр треугольника, равный половине суммы длин сторон:

p = (a + b + c) / 2

Здесь sqrt означает извлечение квадратного корня. Обе формулы могут быть использованы для вычисления площади треугольника в зависимости от имеющихся данных.

Как найти площадь равнобедренного и равностороннего треугольника

Чтобы найти площадь равнобедренного треугольника, необходимо знать длину боковой стороны и высоту, проведенную к основанию. После этого можно воспользоваться формулой:

S = (a * h) / 2

, где a — длина основания, а h — высота, опущенная на основание.

Чтобы найти площадь равностороннего треугольника, необходимо знать длину любой стороны. После этого можно воспользоваться формулой:

S = (a^2 * sqrt(3)) / 4

, где a — длина любой стороны. Также можно использовать формулу через высоту:

S = (a * h) / 2

, где h — высота, опущенная из вершины на основание, а a — длина любой стороны.

Все формулы площади треугольника

Не знаете, как посчитать площадь треугольника? Собрали для вас все возможные формулы. как находить площадь треугольника:

Формула площади треугольника по основанию и высоте:

S = (a * h) / 2

где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника, опущенная на это основание.
Формула Герона:

S = sqrt(p * (p — a) * (p — b) * (p — c))

где S — площадь треугольника, a, b, c — длины сторон треугольника, p — полупериметр треугольника, равный половине суммы длин сторон:

p = (a + b + c) / 2
Формула площади треугольника через две стороны и угол между ними:

S = (a * b * sin(C)) / 2

где S — площадь треугольника, a и b — длины двух сторон треугольника, C — угол между этими сторонами (в радианах), sin — функция синуса.
Формула площади треугольника через радиус вписанной окружности:

S = (a * b * c) / (4 * R)

где S — площадь треугольника, a, b, c — длины сторон треугольника, R — радиус вписанной в треугольник окружности.
Формула площади треугольника через радиус описанной окружности:

S = (a * b * c) / (4 * R)

где S — площадь треугольника, a, b, c — длины сторон треугольника, R — радиус описанной вокруг треугольника окружности.

Часто задаваемые вопросы

✅ Какие есть формулы площади треугольника?

↪ Формула площади треугольника по основанию и высоте: S = (a * h) / 2
Формула Герона: S = sqrt(p * (p — a) * (p — b) * (p — c)), где p = (a + b + c) / 2
Формула площади треугольника через две стороны и угол между ними: S = (a * b * sin(C)) / 2
Формула площади треугольника через радиус вписанной окружности: S = (a * b * c) / (4 * R)
Формула площади треугольника через радиус описанной окружности: S = (a * b * c) / (4 * R)

✅ Как найти площадь треугольника формуле Герона?

↪ Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры.

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

Каждая из идентичных линий называется боковой, а третья – основанием.

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.

Содержание

Площадь равнобедренного треугольника через высоту
Площадь равнобедренного треугольника через стороны
Площадь равнобедренного треугольника через синус угла
Формула площади равнобедренного треугольника через тангенс угла

Площадь равнобедренного треугольника через высоту

И общая их площадь сводится к:

где:

b — размер основания;
h – высота.

Задача №1.

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Ответ: 12 см².

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

Задача №2.

Ответ: 8 см².

Площадь равнобедренного треугольника через синус угла

Задача №3.

Ответ: 4 см².

Формула площади равнобедренного треугольника через тангенс угла

Рисунок 1

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Задача №4.

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45⁰. Требуется найти площадь треугольника OPQ.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90⁰ — угол OPQ.

Вычисляем SOPQ:

SOPQ = 5²/4 * tg 45° = 25/4 * 1 = 6, 25 см²

Ответ: 6,25 см².

ГеометрияПлощадь сферы — формулы и примеры вычислений

ГеометрияТеорема о трех перпендикулярах — правило, формулировка и примеры решения задач

Источник

Площадь треугольника — все формулы, калькулятор онлайн

Площадь треугольника — это численная характеристика, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. В зависимости от типа треугольника и известных исходных данных, площадь треугольника можно рассчитать по различным формулам. Приведенные калькуляторы площади треугольника используют все известные методики и упрощают процесс вычислений.

Треугольник — это геометрическая фигура, образованная соединением отрезков трех точек, не лежащих на одной прямой. Точки называются вершинами треугольника, а отрезки — его сторонами.

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

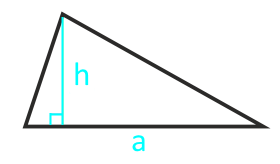
Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

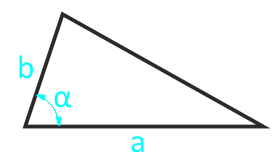
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

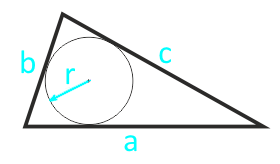
Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

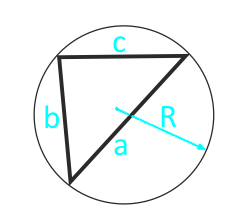
Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

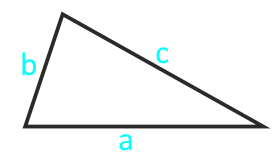
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

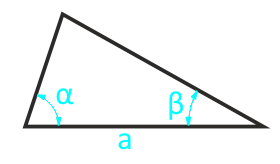
Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°

Калькулятор площади для равнобедренных треугольников

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.

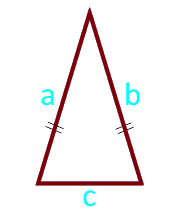
Площадь равнобедренного треугольника по боковым сторонам и основанию — калькулятор:

Формула	Результат
S = ¼ × c × √ (4 × a² — c²)
	Сторона a (a = b)
Сторона c

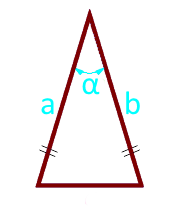
Если известны боковые стороны и угол между ними, то площадь равнобедренного треугольника определяется, как половина произведения квадрата боковой стороны на синус угла между боковыми сторонами.

Площадь равнобедренного треугольника по боковым сторонам и углу между ними:

Формула	Результат
S = ½ × a² × sin (α)
	Боковая сторона a (a = b)
Угол α° между боковыми сторонами

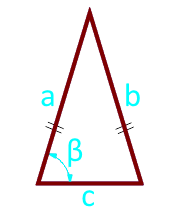
Если известна боковая сторона, основание и углу между ними, то площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними.

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними — расчет:

Формула	Результат
S = ½ ×a × c × sin (β)
	Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной

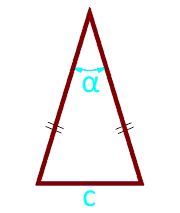
Если известно основание и угол между боковыми сторонами, то площадь равнобедренного треугольника рассчитывается, как четверть отношения квадрата основания на тангенс половинного угла между боковыми сторонами.

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами — онлайн:

Формула	Результат
S = c² ⁄ (4 × tg (½ × α))
	Основание треугольника c
Угол α° между боковыми сторонами

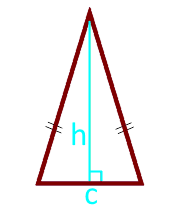
Площадь равнобедренного треугольника по высоте и основанию — калькулятор:

Формула	Результат
S = ½ × c × h
	Основание треугольника c
Высота h

Площадь равносторонних треугольников — онлайн калькулятор, формулы

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

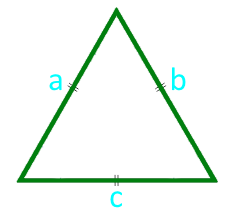
Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.

Площадь равностороннего треугольника по стороне — онлайн расчет:

Формула	Результат
S = ¼ × √(3) × a²
	Сторона a (a = b = c)

Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.

Площадь равностороннего треугольника по высоте:

Формула	Результат
S = h² ⁄ √(3)
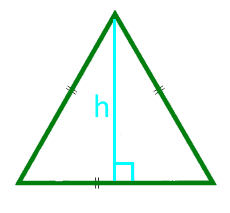	Высота h

Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.

Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:

Формула	Результат
S = 3 × √(3) × r²
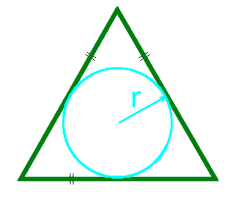	Радиус r вписанной окружности

По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.

Площадь равностороннего треугольника по радиусу описанной окружности:

Формула	Результат
S = ¾ × √(3) × R²
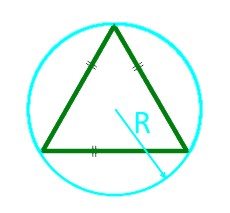	Радиус R описанной окружности

Площадь прямоугольного треугольника — формулы и калькуляторы

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).

По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.

Площадь прямоугольного треугольника по двум катетам — расчет:

Формула	Результат
S = ½ × a × b
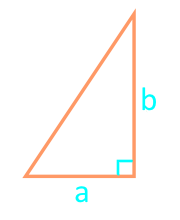	Катет a
Катет b

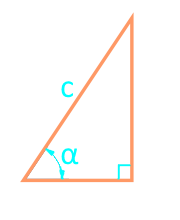
Площадь прямоугольного треугольника через гипотенузу и угол:

Формула	Результат
S = ¼ × c² × sin (2α)
	Сторона c
Угол α

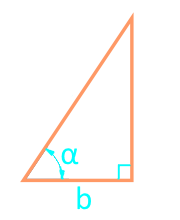
Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:

Формула	Результат
S = ½ × b² × tg (α)
	Сторона b
Угол α

Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:

Формула	Результат
S = d × e
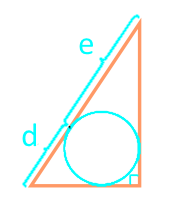	Отрезок d
Отрезок e

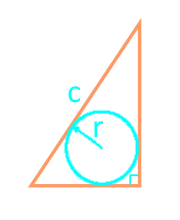
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:

Формула	Результат
S = r × (r + c)
	Сторона с
Радиус r

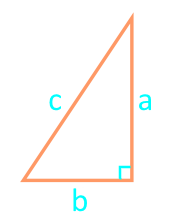
Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)

Площадь прямоугольного треугольника по формуле Герона:

Формула	Результат
S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b)
	Сторона a
Сторона b
Сторона c

Таблица синусов (sin) для расчета площади треугольника

Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя ее вы сможете провести расчеты площади треугольника самостоятельно при помощи формул.

Таблица подходит для вычисления:

Площади прямоугольного треугольника через гипотенузу и угол S = ¼ × c² × sin (2α).
Площади равнобедренного треугольника по боковой стороне, основанию и углу между ними S = ½ ×a × c × sin (β).
Площади равнобедренного треугольника по боковым сторонам и углу между ними S = ½ × a² × sin (α).
Площади произвольного треугольника по стороне и двум прилежащим углам S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)).

Таблица синусов (sin) углов от 0° до 180°:

sin(0°) = 0
sin(1°) = 0.017452
sin(2°) = 0.034899
sin(3°) = 0.052336
sin(4°) = 0.069756
sin(5°) = 0.087156
sin(6°) = 0.104528
sin(7°) = 0.121869
sin(8°) = 0.139173
sin(9°) = 0.156434
sin(10°) = 0.173648
sin(11°) = 0.190809
sin(12°) = 0.207912
sin(13°) = 0.224951
sin(14°) = 0.241922
sin(15°) = 0.258819
sin(16°) = 0.275637
sin(17°) = 0.292372
sin(18°) = 0.309017
sin(19°) = 0.325568
sin(20°) = 0.34202
sin(21°) = 0.358368
sin(22°) = 0.374607
sin(23°) = 0.390731
sin(24°) = 0.406737
sin(25°) = 0.422618
sin(26°) = 0.438371
sin(27°) = 0.45399
sin(28°) = 0.469472
sin(29°) = 0.48481
sin(30°) = 0.5
sin(31°) = 0.515038
sin(32°) = 0.529919
sin(33°) = 0.544639
sin(34°) = 0.559193
sin(35°) = 0.573576
sin(36°) = 0.587785
sin(37°) = 0.601815
sin(38°) = 0.615661
sin(39°) = 0.62932
sin(40°) = 0.642788
sin(41°) = 0.656059
sin(42°) = 0.669131
sin(43°) = 0.681998
sin(44°) = 0.694658
sin(45°) = 0.707107

sin(46°) = 0.71934
sin(47°) = 0.731354
sin(48°) = 0.743145
sin(49°) = 0.75471
sin(50°) = 0.766044
sin(51°) = 0.777146
sin(52°) = 0.788011
sin(53°) = 0.798636
sin(54°) = 0.809017
sin(55°) = 0.819152
sin(56°) = 0.829038
sin(57°) = 0.838671
sin(58°) = 0.848048
sin(59°) = 0.857167
sin(60°) = 0.866025
sin(61°) = 0.87462
sin(62°) = 0.882948
sin(63°) = 0.891007
sin(64°) = 0.898794
sin(65°) = 0.906308
sin(66°) = 0.913545
sin(67°) = 0.920505
sin(68°) = 0.927184
sin(69°) = 0.93358
sin(70°) = 0.939693
sin(71°) = 0.945519
sin(72°) = 0.951057
sin(73°) = 0.956305
sin(74°) = 0.961262
sin(75°) = 0.965926
sin(76°) = 0.970296
sin(77°) = 0.97437
sin(78°) = 0.978148
sin(79°) = 0.981627
sin(80°) = 0.984808
sin(81°) = 0.987688
sin(82°) = 0.990268
sin(83°) = 0.992546
sin(84°) = 0.994522
sin(85°) = 0.996195
sin(86°) = 0.997564
sin(87°) = 0.99863
sin(88°) = 0.999391
sin(89°) = 0.999848
sin(90°) = 1

sin(91°) = 0.999848
sin(92°) = 0.999391
sin(93°) = 0.99863
sin(94°) = 0.997564
sin(95°) = 0.996195
sin(96°) = 0.994522
sin(97°) = 0.992546
sin(98°) = 0.990268
sin(99°) = 0.987688
sin(100°) = 0.984808
sin(101°) = 0.981627
sin(102°) = 0.978148
sin(103°) = 0.97437
sin(104°) = 0.970296
sin(105°) = 0.965926
sin(106°) = 0.961262
sin(107°) = 0.956305
sin(108°) = 0.951057
sin(109°) = 0.945519
sin(110°) = 0.939693
sin(111°) = 0.93358
sin(112°) = 0.927184
sin(113°) = 0.920505
sin(114°) = 0.913545
sin(115°) = 0.906308
sin(116°) = 0.898794
sin(117°) = 0.891007
sin(118°) = 0.882948
sin(119°) = 0.87462
sin(120°) = 0.866025
sin(121°) = 0.857167
sin(122°) = 0.848048
sin(123°) = 0.838671
sin(124°) = 0.829038
sin(125°) = 0.819152
sin(126°) = 0.809017
sin(127°) = 0.798636
sin(128°) = 0.788011
sin(129°) = 0.777146
sin(130°) = 0.766044
sin(131°) = 0.75471
sin(132°) = 0.743145
sin(133°) = 0.731354
sin(134°) = 0.71934
sin(135°) = 0.707107

sin(136°) = 0.694658
sin(137°) = 0.681998
sin(138°) = 0.669131
sin(139°) = 0.656059
sin(140°) = 0.642788
sin(141°) = 0.62932
sin(142°) = 0.615661
sin(143°) = 0.601815
sin(144°) = 0.587785
sin(145°) = 0.573576
sin(146°) = 0.559193
sin(147°) = 0.544639
sin(148°) = 0.529919
sin(149°) = 0.515038
sin(150°) = 0.5
sin(151°) = 0.48481
sin(152°) = 0.469472
sin(153°) = 0.45399
sin(154°) = 0.438371
sin(155°) = 0.422618
sin(156°) = 0.406737
sin(157°) = 0.390731
sin(158°) = 0.374607
sin(159°) = 0.358368
sin(160°) = 0.34202
sin(161°) = 0.325568
sin(162°) = 0.309017
sin(163°) = 0.292372
sin(164°) = 0.275637
sin(165°) = 0.258819
sin(166°) = 0.241922
sin(167°) = 0.224951
sin(168°) = 0.207912
sin(169°) = 0.190809
sin(170°) = 0.173648
sin(171°) = 0.156434
sin(172°) = 0.139173
sin(173°) = 0.121869
sin(174°) = 0.104528
sin(175°) = 0.087156
sin(176°) = 0.069756
sin(177°) = 0.052336
sin(178°) = 0.034899
sin(179°) = 0.017452
sin(180°) = 0

Таблица синусов (sin) углов от 181° до 360°:

sin(181°) = -0.017452
sin(182°) = -0.034899
sin(183°) = -0.052336
sin(184°) = -0.069756
sin(185°) = -0.087156
sin(186°) = -0.104528
sin(187°) = -0.121869
sin(188°) = -0.139173
sin(189°) = -0.156434
sin(190°) = -0.173648
sin(191°) = -0.190809
sin(192°) = -0.207912
sin(193°) = -0.224951
sin(194°) = -0.241922
sin(195°) = -0.258819
sin(196°) = -0.275637
sin(197°) = -0.292372
sin(198°) = -0.309017
sin(199°) = -0.325568
sin(200°) = -0.34202
sin(201°) = -0.358368
sin(202°) = -0.374607
sin(203°) = -0.390731
sin(204°) = -0.406737
sin(205°) = -0.422618
sin(206°) = -0.438371
sin(207°) = -0.45399
sin(208°) = -0.469472
sin(209°) = -0.48481
sin(210°) = -0.5
sin(211°) = -0.515038
sin(212°) = -0.529919
sin(213°) = -0.544639
sin(214°) = -0.559193
sin(215°) = -0.573576
sin(216°) = -0.587785
sin(217°) = -0.601815
sin(218°) = -0.615661
sin(219°) = -0.62932
sin(220°) = -0.642788
sin(221°) = -0.656059
sin(222°) = -0.669131
sin(223°) = -0.681998
sin(224°) = -0.694658
sin(225°) = -0.707107

sin(226°) = -0.71934
sin(227°) = -0.731354
sin(228°) = -0.743145
sin(229°) = -0.75471
sin(230°) = -0.766044
sin(231°) = -0.777146
sin(232°) = -0.788011
sin(233°) = -0.798636
sin(234°) = -0.809017
sin(235°) = -0.819152
sin(236°) = -0.829038
sin(237°) = -0.838671
sin(238°) = -0.848048
sin(239°) = -0.857167
sin(240°) = -0.866025
sin(241°) = -0.87462
sin(242°) = -0.882948
sin(243°) = -0.891007
sin(244°) = -0.898794
sin(245°) = -0.906308
sin(246°) = -0.913545
sin(247°) = -0.920505
sin(248°) = -0.927184
sin(249°) = -0.93358
sin(250°) = -0.939693
sin(251°) = -0.945519
sin(252°) = -0.951057
sin(253°) = -0.956305
sin(254°) = -0.961262
sin(255°) = -0.965926
sin(256°) = -0.970296
sin(257°) = -0.97437
sin(258°) = -0.978148
sin(259°) = -0.981627
sin(260°) = -0.984808
sin(261°) = -0.987688
sin(262°) = -0.990268
sin(263°) = -0.992546
sin(264°) = -0.994522
sin(265°) = -0.996195
sin(266°) = -0.997564
sin(267°) = -0.99863
sin(268°) = -0.999391
sin(269°) = -0.999848
sin(270°) = -1

sin(271°) = -0.999848
sin(272°) = -0.999391
sin(273°) = -0.99863
sin(274°) = -0.997564
sin(275°) = -0.996195
sin(276°) = -0.994522
sin(277°) = -0.992546
sin(278°) = -0.990268
sin(279°) = -0.987688
sin(280°) = -0.984808
sin(281°) = -0.981627
sin(282°) = -0.978148
sin(283°) = -0.97437
sin(284°) = -0.970296
sin(285°) = -0.965926
sin(286°) = -0.961262
sin(287°) = -0.956305
sin(288°) = -0.951057
sin(289°) = -0.945519
sin(290°) = -0.939693
sin(291°) = -0.93358
sin(292°) = -0.927184
sin(293°) = -0.920505
sin(294°) = -0.913545
sin(295°) = -0.906308
sin(296°) = -0.898794
sin(297°) = -0.891007
sin(298°) = -0.882948
sin(299°) = -0.87462
sin(300°) = -0.866025
sin(301°) = -0.857167
sin(302°) = -0.848048
sin(303°) = -0.838671
sin(304°) = -0.829038
sin(305°) = -0.819152
sin(306°) = -0.809017
sin(307°) = -0.798636
sin(308°) = -0.788011
sin(309°) = -0.777146
sin(310°) = -0.766044
sin(311°) = -0.75471
sin(312°) = -0.743145
sin(313°) = -0.731354
sin(314°) = -0.71934
sin(315°) = -0.707107

sin(316°) = -0.694658
sin(317°) = -0.681998
sin(318°) = -0.669131
sin(319°) = -0.656059
sin(320°) = -0.642788
sin(321°) = -0.62932
sin(322°) = -0.615661
sin(323°) = -0.601815
sin(324°) = -0.587785
sin(325°) = -0.573576
sin(326°) = -0.559193
sin(327°) = -0.544639
sin(328°) = -0.529919
sin(329°) = -0.515038
sin(330°) = -0.5
sin(331°) = -0.48481
sin(332°) = -0.469472
sin(333°) = -0.45399
sin(334°) = -0.438371
sin(335°) = -0.422618
sin(336°) = -0.406737
sin(337°) = -0.390731
sin(338°) = -0.374607
sin(339°) = -0.358368
sin(340°) = -0.34202
sin(341°) = -0.325568
sin(342°) = -0.309017
sin(343°) = -0.292372
sin(344°) = -0.275637
sin(345°) = -0.258819
sin(346°) = -0.241922
sin(347°) = -0.224951
sin(348°) = -0.207912
sin(349°) = -0.190809
sin(350°) = -0.173648
sin(351°) = -0.156434
sin(352°) = -0.139173
sin(353°) = -0.121869
sin(354°) = -0.104528
sin(355°) = -0.087156
sin(356°) = -0.069756
sin(357°) = -0.052336
sin(358°) = -0.034899
sin(359°) = -0.017452
sin(360°) = 0

Таблица тангенсов (tg) для расчета площади треугольника

Таблица тангенсов — это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. С ее помощью вы сможете провести расчеты площади треугольника самостоятельно по следующим формулам:

S = ½ × b² × tg (α) — площадь прямоугольного треугольника через катет и угол.
S = c² ⁄ (4 × tg (½ × α)) — площадь равнобедренного треугольника по основанию и углу между боковыми сторонами.

Таблица тангенсов (tg) углов от 0° до 180°:

tg(0°) = 0
tg(1°) = 0.01746
tg(2°) = 0.03492
tg(3°) = 0.05241
tg(4°) = 0.06993
tg(5°) = 0.08749
tg(6°) = 0.1051
tg(7°) = 0.12278
tg(8°) = 0.14054
tg(9°) = 0.15838
tg(10°) = 0.17633
tg(11°) = 0.19438
tg(12°) = 0.21256
tg(13°) = 0.23087
tg(14°) = 0.24933
tg(15°) = 0.26795
tg(16°) = 0.28675
tg(17°) = 0.30573
tg(18°) = 0.32492
tg(19°) = 0.34433
tg(20°) = 0.36397
tg(21°) = 0.38386
tg(22°) = 0.40403
tg(23°) = 0.42447
tg(24°) = 0.44523
tg(25°) = 0.46631
tg(26°) = 0.48773
tg(27°) = 0.50953
tg(28°) = 0.53171
tg(29°) = 0.55431
tg(30°) = 0.57735
tg(31°) = 0.60086
tg(32°) = 0.62487
tg(33°) = 0.64941
tg(34°) = 0.67451
tg(35°) = 0.70021
tg(36°) = 0.72654
tg(37°) = 0.75355
tg(38°) = 0.78129
tg(39°) = 0.80978
tg(40°) = 0.8391
tg(41°) = 0.86929
tg(42°) = 0.9004
tg(43°) = 0.93252
tg(44°) = 0.96569
tg(45°) = 1
tg(46°) = 1.03553
tg(47°) = 1.07237
tg(48°) = 1.11061
tg(49°) = 1.15037
tg(50°) = 1.19175
tg(51°) = 1.2349
tg(52°) = 1.27994
tg(53°) = 1.32704
tg(54°) = 1.37638
tg(55°) = 1.42815
tg(56°) = 1.48256
tg(57°) = 1.53986
tg(58°) = 1.60033
tg(59°) = 1.66428
tg(60°) = 1.73205

tg(61°) = 1.80405
tg(62°) = 1.88073
tg(63°) = 1.96261
tg(64°) = 2.0503
tg(65°) = 2.14451
tg(66°) = 2.24604
tg(67°) = 2.35585
tg(68°) = 2.47509
tg(69°) = 2.60509
tg(70°) = 2.74748
tg(71°) = 2.90421
tg(72°) = 3.07768
tg(73°) = 3.27085
tg(74°) = 3.48741
tg(75°) = 3.73205
tg(76°) = 4.01078
tg(77°) = 4.33148
tg(78°) = 4.70463
tg(79°) = 5.14455
tg(80°) = 5.67128
tg(81°) = 6.31375
tg(82°) = 7.11537
tg(83°) = 8.14435
tg(84°) = 9.51436
tg(85°) = 11.43005
tg(86°) = 14.30067
tg(87°) = 19.08114
tg(88°) = 28.63625
tg(89°) = 57.28996
tg(90°) = ∞
tg(91°) = -57.28996
tg(92°) = -28.63625
tg(93°) = -19.08114
tg(94°) = -14.30067
tg(95°) = -11.43005
tg(96°) = -9.51436
tg(97°) = -8.14435
tg(98°) = -7.11537
tg(99°) = -6.31375
tg(100°) = -5.67128
tg(101°) = -5.14455
tg(102°) = -4.70463
tg(103°) = -4.33148
tg(104°) = -4.01078
tg(105°) = -3.73205
tg(106°) = -3.48741
tg(107°) = -3.27085
tg(108°) = -3.07768
tg(109°) = -2.90421
tg(110°) = -2.74748
tg(111°) = -2.60509
tg(112°) = -2.47509
tg(113°) = -2.35585
tg(114°) = -2.24604
tg(115°) = -2.14451
tg(116°) = -2.0503
tg(117°) = -1.96261
tg(118°) = -1.88073
tg(119°) = -1.80405
tg(120°) = -1.73205

tg(121°) = -1.66428
tg(122°) = -1.60033
tg(123°) = -1.53986
tg(124°) = -1.48256
tg(125°) = -1.42815
tg(126°) = -1.37638
tg(127°) = -1.32704
tg(128°) = -1.27994
tg(129°) = -1.2349
tg(130°) = -1.19175
tg(131°) = -1.15037
tg(132°) = -1.11061
tg(133°) = -1.07237
tg(134°) = -1.03553
tg(135°) = -1
tg(136°) = -0.96569
tg(137°) = -0.93252
tg(138°) = -0.9004
tg(139°) = -0.86929
tg(140°) = -0.8391
tg(141°) = -0.80978
tg(142°) = -0.78129
tg(143°) = -0.75355
tg(144°) = -0.72654
tg(145°) = -0.70021
tg(146°) = -0.67451
tg(147°) = -0.64941
tg(148°) = -0.62487
tg(149°) = -0.60086
tg(150°) = -0.57735
tg(151°) = -0.55431
tg(152°) = -0.53171
tg(153°) = -0.50953
tg(154°) = -0.48773
tg(155°) = -0.46631
tg(156°) = -0.44523
tg(157°) = -0.42447
tg(158°) = -0.40403
tg(159°) = -0.38386
tg(160°) = -0.36397
tg(161°) = -0.34433
tg(162°) = -0.32492
tg(163°) = -0.30573
tg(164°) = -0.28675
tg(165°) = -0.26795
tg(166°) = -0.24933
tg(167°) = -0.23087
tg(168°) = -0.21256
tg(169°) = -0.19438
tg(170°) = -0.17633
tg(171°) = -0.15838
tg(172°) = -0.14054
tg(173°) = -0.12278
tg(174°) = -0.1051
tg(175°) = -0.08749
tg(176°) = -0.06993
tg(177°) = -0.05241
tg(178°) = -0.03492
tg(179°) = -0.01746
tg(180°) = 0

Таблица тангенсов (tg) углов от 181° до 360°:

tg(181°) = 0.01746
tg(182°) = 0.03492
tg(183°) = 0.05241
tg(184°) = 0.06993
tg(185°) = 0.08749
tg(186°) = 0.1051
tg(187°) = 0.12278
tg(188°) = 0.14054
tg(189°) = 0.15838
tg(190°) = 0.17633
tg(191°) = 0.19438
tg(192°) = 0.21256
tg(193°) = 0.23087
tg(194°) = 0.24933
tg(195°) = 0.26795
tg(196°) = 0.28675
tg(197°) = 0.30573
tg(198°) = 0.32492
tg(199°) = 0.34433
tg(200°) = 0.36397
tg(201°) = 0.38386
tg(202°) = 0.40403
tg(203°) = 0.42447
tg(204°) = 0.44523
tg(205°) = 0.46631
tg(206°) = 0.48773
tg(207°) = 0.50953
tg(208°) = 0.53171
tg(209°) = 0.55431
tg(210°) = 0.57735
tg(211°) = 0.60086
tg(212°) = 0.62487
tg(213°) = 0.64941
tg(214°) = 0.67451
tg(215°) = 0.70021
tg(216°) = 0.72654
tg(217°) = 0.75355
tg(218°) = 0.78129
tg(219°) = 0.80978
tg(220°) = 0.8391
tg(221°) = 0.86929
tg(222°) = 0.9004
tg(223°) = 0.93252
tg(224°) = 0.96569
tg(225°) = 1
tg(226°) = 1.03553
tg(227°) = 1.07237
tg(228°) = 1.11061
tg(229°) = 1.15037
tg(230°) = 1.19175
tg(231°) = 1.2349
tg(232°) = 1.27994
tg(233°) = 1.32704
tg(234°) = 1.37638
tg(235°) = 1.42815
tg(236°) = 1.48256
tg(237°) = 1.53986
tg(238°) = 1.60033
tg(239°) = 1.66428
tg(240°) = 1.73205

tg(241°) = 1.80405
tg(242°) = 1.88073
tg(243°) = 1.96261
tg(244°) = 2.0503
tg(245°) = 2.14451
tg(246°) = 2.24604
tg(247°) = 2.35585
tg(248°) = 2.47509
tg(249°) = 2.60509
tg(250°) = 2.74748
tg(251°) = 2.90421
tg(252°) = 3.07768
tg(253°) = 3.27085
tg(254°) = 3.48741
tg(255°) = 3.73205
tg(256°) = 4.01078
tg(257°) = 4.33148
tg(258°) = 4.70463
tg(259°) = 5.14455
tg(260°) = 5.67128
tg(261°) = 6.31375
tg(262°) = 7.11537
tg(263°) = 8.14435
tg(264°) = 9.51436
tg(265°) = 11.43005
tg(266°) = 14.30067
tg(267°) = 19.08114
tg(268°) = 28.63625
tg(269°) = 57.28996
tg(270°) = ∞
tg(271°) = -57.28996
tg(272°) = -28.63625
tg(273°) = -19.08114
tg(274°) = -14.30067
tg(275°) = -11.43005
tg(276°) = -9.51436
tg(277°) = -8.14435
tg(278°) = -7.11537
tg(279°) = -6.31375
tg(280°) = -5.67128
tg(281°) = -5.14455
tg(282°) = -4.70463
tg(283°) = -4.33148
tg(284°) = -4.01078
tg(285°) = -3.73205
tg(286°) = -3.48741
tg(287°) = -3.27085
tg(288°) = -3.07768
tg(289°) = -2.90421
tg(290°) = -2.74748
tg(291°) = -2.60509
tg(292°) = -2.47509
tg(293°) = -2.35585
tg(294°) = -2.24604
tg(295°) = -2.14451
tg(296°) = -2.0503
tg(297°) = -1.96261
tg(298°) = -1.88073
tg(299°) = -1.80405
tg(300°) = -1.73205

tg(301°) = -1.66428
tg(302°) = -1.60033
tg(303°) = -1.53986
tg(304°) = -1.48256
tg(305°) = -1.42815
tg(306°) = -1.37638
tg(307°) = -1.32704
tg(308°) = -1.27994
tg(309°) = -1.2349
tg(310°) = -1.19175
tg(311°) = -1.15037
tg(312°) = -1.11061
tg(313°) = -1.07237
tg(314°) = -1.03553
tg(315°) = -1
tg(316°) = -0.96569
tg(317°) = -0.93252
tg(318°) = -0.9004
tg(319°) = -0.86929
tg(320°) = -0.8391
tg(321°) = -0.80978
tg(322°) = -0.78129
tg(323°) = -0.75355
tg(324°) = -0.72654
tg(325°) = -0.70021
tg(326°) = -0.67451
tg(327°) = -0.64941
tg(328°) = -0.62487
tg(329°) = -0.60086
tg(330°) = -0.57735
tg(331°) = -0.55431
tg(332°) = -0.53171
tg(333°) = -0.50953
tg(334°) = -0.48773
tg(335°) = -0.46631
tg(336°) = -0.44523
tg(337°) = -0.42447
tg(338°) = -0.40403
tg(339°) = -0.38386
tg(340°) = -0.36397
tg(341°) = -0.34433
tg(342°) = -0.32492
tg(343°) = -0.30573
tg(344°) = -0.28675
tg(345°) = -0.26795
tg(346°) = -0.24933
tg(347°) = -0.23087
tg(348°) = -0.21256
tg(349°) = -0.19438
tg(350°) = -0.17633
tg(351°) = -0.15838
tg(352°) = -0.14054
tg(353°) = -0.12278
tg(354°) = -0.1051
tg(355°) = -0.08749
tg(356°) = -0.06993
tg(357°) = -0.05241
tg(358°) = -0.03492
tg(359°) = -0.01746
tg(360°) = 0

Площадь треугольника можно посчитать самостоятельно по формулам, или воспользоваться для этого онлайн калькулятором. В рассмотренном материале приведены как формулы и таблицы синусов, тангенсов, так и калькуляторы с возможностью расчета площади 21 способом.

Источник

Каждая из идентичных линий называется боковой, а третья – основанием.