Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

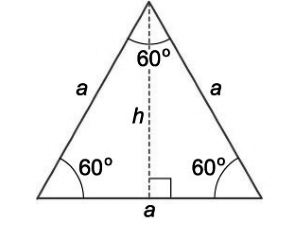
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
Основание треугольника:
a =
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
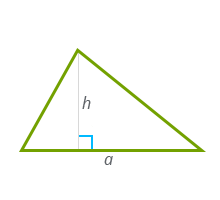
1) через основание и высоту
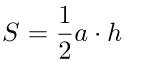
a – основание треугольника,
h – высота треугольника.
2) через две стороны и угол
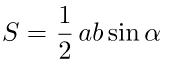
a, b – стороны треугольника,
α – угол между сторонами.
3) По трем сторонам. Формула Герона.
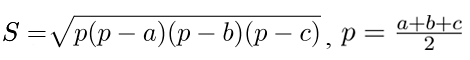
a, b, с – стороны треугольника,
p – полупериметр треугольника.
4) Через радиус вписанной окружности.
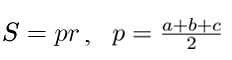
a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
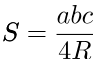
a, b, с – стороны треугольника,
R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
В этой статье собраны наиболее популярные формулы для нахождения площади треугольника.
Как найти площадь треугольника по высоте?
Если известно основание и высота, проведенная к основанию треугольника, можно вычислить площадь треугольника.
(S=frac{1}{2}a*h)
Калькулятор площади треугольника по высоте и основанию
Основание треугольника:
Высота треугольника:
Как найти площадь треугольника: формула Герона
Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры:
(S=sqrt{p(p-a)(p-b)(p-c)})
где (a,b,c) – стороны треугольника, (p=frac{a+b+c}{2}) – его полупериметр.
Калькулятор площади треугольника по трем сторонам
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Формула нахождения площади треугольника по окружности
Как вычислить площадь треугольника, если известна окружность и три его стороны?
(S=frac{a*b*c}{4R})
Калькулятор площади треугольника по трем сторонам и радиусу описанной окружности
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус описанной окружности R:
Как найти площадь прямоугольного треугольника
Чтобы найти площадь прямоугольного треугольника, необходимо знать длины двух катетов. После этого можно воспользоваться формулой:
S = (a * b) / 2
, где a и b — длины катетов. Просто перемножьте значения длин катетов и разделите результат на два, чтобы найти площадь прямоугольного треугольника.
Как узнать площадь треугольника по радиусу и полупериметру
Можно найти площадь треугольника, когда мы знаем полупериметр и радиус вписанной окружности:
(S=pr)
где r — радиус вписанной окружности, (p=frac{a+b+c}{2})– его полупериметр.
Калькулятор площади треугольника по трем сторонам и радиусу вписанной окружности
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус вписанной окружности R:
Как найти площадь треугольника по стороне и тангенсу: формула
Формула нахождения площади по стороне и тангенсу углов треугольника:
(S=frac{c^2}{2(ctgA+ctgB)})
Основные формулы площади треугольника для учащихся 5-6 классов
Для ученика 5-6 класса обычно достаточно знать две формулы для вычисления площади треугольника:
-
Формула площади произвольного треугольника по основанию и высоте:
S = (a * h) / 2
где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника, опущенная на это основание.
-
Формула Герона:
S = sqrt(p * (p — a) * (p — b) * (p — c))
где S — площадь треугольника, a, b, c — длины сторон треугольника, p — полупериметр треугольника, равный половине суммы длин сторон:
p = (a + b + c) / 2
Здесь sqrt означает извлечение квадратного корня. Обе формулы могут быть использованы для вычисления площади треугольника в зависимости от имеющихся данных.
Как найти площадь равнобедренного и равностороннего треугольника
Чтобы найти площадь равнобедренного треугольника, необходимо знать длину боковой стороны и высоту, проведенную к основанию. После этого можно воспользоваться формулой:
S = (a * h) / 2
, где a — длина основания, а h — высота, опущенная на основание.
Чтобы найти площадь равностороннего треугольника, необходимо знать длину любой стороны. После этого можно воспользоваться формулой:
S = (a^2 * sqrt(3)) / 4
, где a — длина любой стороны. Также можно использовать формулу через высоту:
S = (a * h) / 2
, где h — высота, опущенная из вершины на основание, а a — длина любой стороны.
Все формулы площади треугольника
Не знаете, как посчитать площадь треугольника? Собрали для вас все возможные формулы. как находить площадь треугольника:
-
Формула площади треугольника по основанию и высоте:
S = (a * h) / 2
где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника, опущенная на это основание.
-
Формула Герона:
S = sqrt(p * (p — a) * (p — b) * (p — c))
где S — площадь треугольника, a, b, c — длины сторон треугольника, p — полупериметр треугольника, равный половине суммы длин сторон:
p = (a + b + c) / 2
-
Формула площади треугольника через две стороны и угол между ними:
S = (a * b * sin(C)) / 2
где S — площадь треугольника, a и b — длины двух сторон треугольника, C — угол между этими сторонами (в радианах), sin — функция синуса.
-
Формула площади треугольника через радиус вписанной окружности:
S = (a * b * c) / (4 * R)
где S — площадь треугольника, a, b, c — длины сторон треугольника, R — радиус вписанной в треугольник окружности.
-
Формула площади треугольника через радиус описанной окружности:
S = (a * b * c) / (4 * R)
где S — площадь треугольника, a, b, c — длины сторон треугольника, R — радиус описанной вокруг треугольника окружности.
Часто задаваемые вопросы
✅ Какие есть формулы площади треугольника?
↪ Формула площади треугольника по основанию и высоте: S = (a * h) / 2
Формула Герона: S = sqrt(p * (p — a) * (p — b) * (p — c)), где p = (a + b + c) / 2
Формула площади треугольника через две стороны и угол между ними: S = (a * b * sin(C)) / 2
Формула площади треугольника через радиус вписанной окружности: S = (a * b * c) / (4 * R)
Формула площади треугольника через радиус описанной окружности: S = (a * b * c) / (4 * R)
✅ Как найти площадь треугольника формуле Герона?
↪ Формула площади треугольника Герона помогает вычислить ее по трем сторонам фигуры.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Ирина Алексеевна Антоненко
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.
Рассмотрим пример.
Пример 1
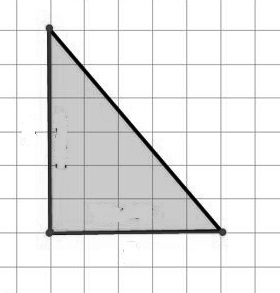
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Решение.
Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется
$5cdot 6=30$
Тогда площадь треугольника равняется
$30:2=15$
Ответ: $15$.
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Теорема 1
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=frac{1}{2}αh$
где $a$ — длина стороны, $h$ — высота, проведенная к ней.
Доказательство.
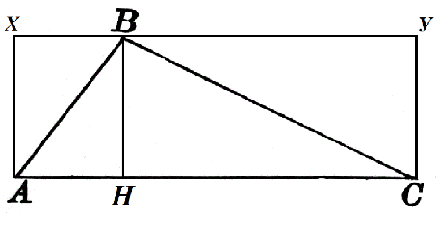
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
Площадь прямоугольника $AXBH$ равняется $hcdot AH$, а прямоугольника $HBYC$ равняется $hcdot HC$. Тогда
$S_ABH=frac{1}{2}hcdot AH$, $S_CBH=frac{1}{2}hcdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=frac{1}{2}hcdot AH+frac{1}{2}hcdot HC=frac{1}{2}hcdot (AH+HC)=frac{1}{2}αh$
Теорема доказана.
«Как найти площадь треугольника. Формулы треугольника» 👇
Пример 2
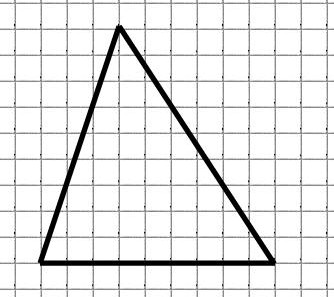
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Решение.
Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим
$S=frac{1}{2}cdot 9cdot 9=40,5$
Ответ: $40,5$.
Формула Герона
Теорема 2
Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом
$S=sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
здесь $ρ$ означает полупериметр этого треугольника.
Доказательство.
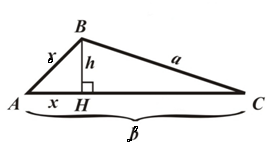
Рассмотрим следующий рисунок:
По теореме Пифагора из треугольника $ABH$ получим
$h^2=γ^2-x^2$
Из треугольника $CBH$, по теореме Пифагора, имеем
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Из этих двух соотношений получаем равенство
$γ^2-x^2=α^2-β^2+2βx-x^2$
То есть
$x=frac{γ^2-α^2+β^2}{2β}$
Получим
$h^2=γ^2-(frac{γ^2-α^2+β^2}{2β})^2$
$h^2=frac{(α^2-(γ-β)^2 )((γ+β)^2-α^2)}{4β^2}$
$h^2=frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$
Так как $ρ=frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит
$h^2=frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$
$h^2=frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$
$h=sqrt{frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$
$h=frac{2}{β}sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=frac{1}{2} βh=frac{β}{2}cdot frac{2}{β} sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
Теорема доказана.
Площадь равностороннего треугольника
Теорема 3
Площадь равностороннего треугольника определяется как произведение квадрата стороны с числом $frac{sqrt{3}}{4}$.
Математически это выглядит следующим образом
$S=frac{α^2sqrt{3}}{4}$
где $α$ – сторона треугольника.
Доказательство.
Пусть нам дан равносторонний треугольник, у которого сторона равняется $α$. Проведем высоту $h$ (рис. 5).
Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора
$h^2=α^2-frac{α^2}{4}$
$h^2=frac{3}{4} α^2$
$h=frac{αsqrt{3}}{2}$
Значит по теореме 1:
$S=frac{α^2sqrt{3}}{4}$
Теорема доказана.
Пример 3
Найти площадь равностороннего треугольника, если его сторона равняется $2$.
Решение.
Используя теорему 3, получим
$S=frac{4sqrt{3}}{4}=sqrt{3}$
Ответ: $sqrt{3}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме