Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
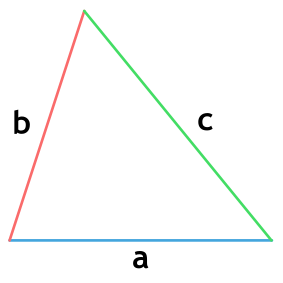
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

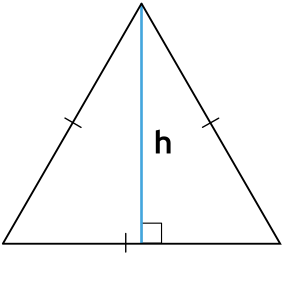
Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
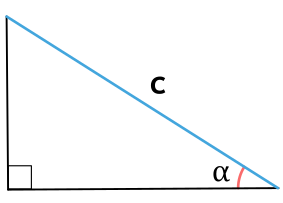
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
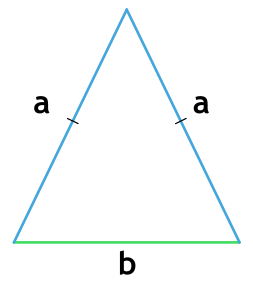
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
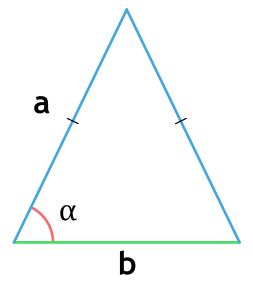
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
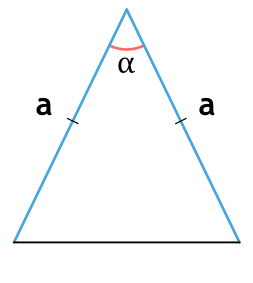
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
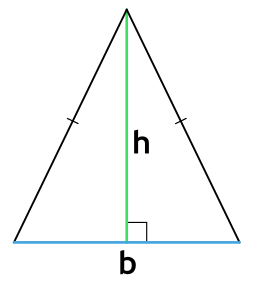
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
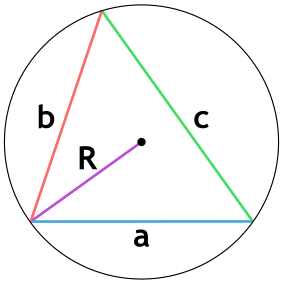
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
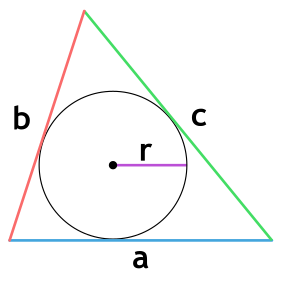
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Как найти площадь треугольника, если известен угол
Знания лишь одного параметра (величины угла) не достаточно для нахождения площади треугольника. Если же есть какие-либо дополнительные размеры, то для определения площади можно выбрать одну из формул, в которых в качестве одной из известных переменных используется и величина угла. Несколько таких формул, применяемых наиболее часто, приведено ниже.

Инструкция
Если кроме величины угла (γ), образованного двумя сторонами треугольника, известны и длины этих сторон (A и B), то площадь (S) фигуры можно определить, как половину от произведения длин известных сторон на синус этого известного угла: S=½×A×B×sin(γ).
Если кроме величины одного угла (γ), известна и длина прилегающей к ней стороны (A), а также величина второго угла (β), тоже прилегающего к этой стороне, то площадь (S) треугольника можно вычислить, если найти частное от деления возведенной в квадрат длины единственной известной стороны на удвоенную сумму котангенсов обоих известных углов: S=½×A²/(ctg(γ)+ctg(β)).
При тех же исходных данных, когда в треугольнике известны величины двух углов (γ и β) и длина стороны между ними (A), можно рассчитать площадь (S) фигуры и немного по-другому. Для этого потребуется найти произведение возведенной в квадрат длины известной стороны на синусы обоих углов, а полученный результат разделить на удвоенный синус суммы этих углов: S=½×A²×sin(γ)×sin(β)/sin(γ+β).
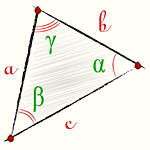
Если известны величины всех трех углов (α, β, γ) в вершинах треугольника, а также длина хотя бы одной из его сторон (A), то площадь (S) можно определить, вычислив дробь, в числителе которой будет произведение возведенной в квадрат длины известной стороны на синусы прилегающих к ней углов, а в знаменателе — удвоенный синус угла, лежащего напротив известной стороны: S=½×A²×sin(γ)×sin(β)/sin(α).
Если же величины всех трех углов известны (α, β, γ), а данных о длинах сторон нет, но дан радиус (R) описанной возле треугольника окружности, то этот набор данных тоже позволит вычислить площадь (S) фигуры. Для этого надо удвоить произведение возведенного в квадрат радиуса на синусы всех трех углов: S=2×R²×sin(α)×sin(β)×sin(γ).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Площадь треугольника через углы, формула
Площадь треугольника через две стороны и угол между ними, формула
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
[ S = frac{1}{2} a b sin(γ) ]
[ S = frac{1}{2} a c sin(β) ]
[ S = frac{1}{2} b c sin(α) ]
Площадь треугольника через одну сторону и прилежащие к ней углы, формула
Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус противолежащего угла.
Противолежащий угол вычисляется по формуле:
[ γ = 180° — (α + β) ]
[ β = 180° — (α + γ) ]
[ α = 180° — (β + γ) ]
Площадь треугольника вычисляется по формулам:
[ S = frac{1}{2} a^2 frac{sin(β)sin(γ)}{sin(α)} ]
[ S = frac{1}{2} b^2 frac{sin(α)sin(γ)}{sin(β)} ]
[ S = frac{1}{2} c^2 frac{sin(α)sin(β)}{sin(γ)} ]
Ссылки по теме
Площадь треугольника через углы |
стр. 303 |
|---|

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
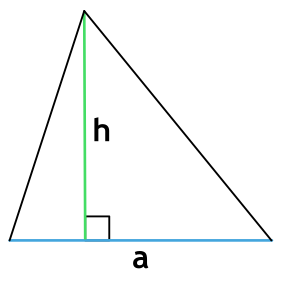
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a — длина основания
h — высота, проведенная к основанию
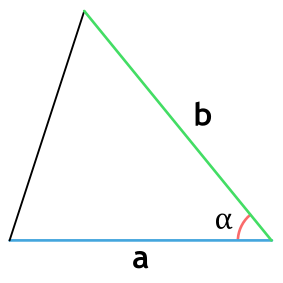
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b — стороны треугольника
α — угол между сторонами a и b
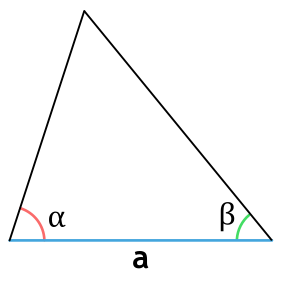
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 — (alpha + beta)}
a — сторона треугольника
α и β — прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c — стороны треугольника
R — радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c — стороны треугольника
r — радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c — стороны треугольника
p — полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
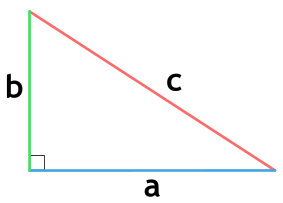
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b — стороны треугольника
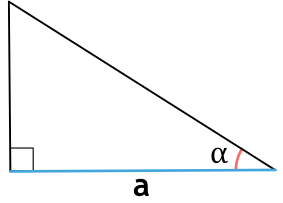
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c — гипотенуза прямоугольного треугольника
α — прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a — катет прямоугольного треугольника
α — прилежащий к катету a угол
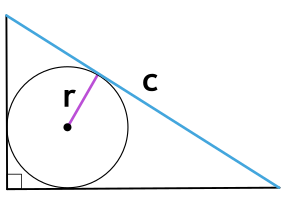
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r — радиус вписанной окружности
c — гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 — отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c — стороны треугольника
p — полупериметр треугольника
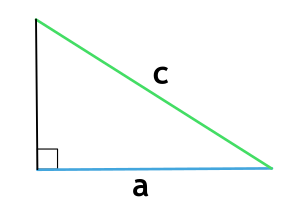
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2}}
a — катет прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 — b^2}}
a — боковая сторона равнобедренного треугольника
b — основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a — боковая сторона равнобедренного треугольника
b — основание равнобедренного треугольника
α — угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b — основание равнобедренного треугольника
h — высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a — боковые стороны равнобедренного треугольника
α — угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b — основание равнобедренного треугольника
α — угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник — треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a — сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h — высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R — радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r — радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 — 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 — 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 — 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 — 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 — 4^2} = sqrt{4 cdot 49 — 16} = sqrt{196 — 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 — 30^2} = dfrac{30}{4} sqrt{4 cdot 289 — 900} = dfrac{30}{4} sqrt{1156 — 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²