Задание 16587
Площадь треугольника можно вычислить по формуле$$S=frac{abc}{4R}$$, где $$a$$, $$b$$, $$c$$ — стороны треугольника, a $$R$$ — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите $$b$$, если $$a=13$$, $$c=15$$, $$S=84$$ и $$R=frac{65}{8}$$.
Ответ: 14
Видео-решение
Предложить свое решение / сообщить об ошибке
Решите задачи
| 1 | Площадь прямоугольного треугольника равна 364,5 cdot sqrt{3}. Один из острых углов равен 30°. Найдите длину гипотенузы. | Смотреть видеоразбор >> |
| 2 | Площадь равнобедренного треугольника равна sqrt{3}. Угол, лежащий напротив основания, равен 120°. Найдите длину боковой стороны треугольника. | Смотреть видеоразбор >> |
| 3 | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. | Смотреть видеоразбор >> |
| 4 | Площадь прямоугольного треугольника равна 840,5 cdot sqrt{3}. Один из острых углов равен 60°. Найдите длину гипотенузы. | Смотреть видеоразбор >> |
| 5 | Площадь прямоугольного треугольника равна 180,5 cdot sqrt{3}. Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу. | Смотреть видеоразбор >> |
| 6 | Площадь прямоугольного треугольника равна 200sqrt{3}. Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла. | Смотреть видеоразбор >> |
| 7 | Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника. | Смотреть видеоразбор >> |
| 8 | В прямоугольном треугольнике гипотенуза равна 6, а один из острых углов равен 45°. Найдите площадь треугольника. | Смотреть видеоразбор >> |
| 9 | Периметр равнобедренного треугольника равен 240, а боковая сторона – 75. Найдите площадь треугольника. | Смотреть видеоразбор >> |
| 10 | Площадь прямоугольного треугольника равна frac{2888sqrt{3}}{3}. Один из острых углов равен 30°.Найдите длину катета,прилежащего к этому углу. | Смотреть видеоразбор >> |
| 11 | В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника. | Смотреть видеоразбор >> |
| 12 | Площадь прямоугольного треугольника равна frac{242sqrt{3}}{3}. Один из острых углов равен 60°.Найдите длину катета,лежащего напротив этого угла. | Смотреть видеоразбор >> |
| 13 | Периметр равнобедренного треугольника равен 250, а основание – 80. Найдите площадь треугольника. | Смотреть видеоразбор >> |
| 14 | Периметр ромба равен 180, а один из углов равен 30°. Найдите площадь ромба. | Смотреть видеоразбор >> |
| 15 | Периметр квадрата равен 8. Найдите площадь квадрата. | Смотреть видеоразбор >> |
| 16 | Основания трапеции равны 9 и 45,одна из боковых сторон равна 28,а косинус угла между ней и одним из оснований равен frac{4sqrt{2}}{9}. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 17 | Основания трапеции равны 5 и 27, одна из боковых сторон равна 27sqrt{3}, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 18 | Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба. | Смотреть видеоразбор >> |
| 19 | В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC. | Смотреть видеоразбор >> |
| 20 | Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6. | Смотреть видеоразбор >> |
| 21 | Основания равнобедренной трапеции равны 14 и 26, а её боковые стороны равны 10. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 22 | Сторона ромба равна 52, а диагональ равна 40. Найдите площадь ромба. | Смотреть видеоразбор >> |
| 23 | Основания трапеции равны 6 и 20, одна из боковых сторон равна 13sqrt{2}, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 24 | Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба. | Смотреть видеоразбор >> |
| 25 | Высота BH ромба делит его сторону AD на отрезки AH=5 и HD=8. Найдите площадь ромба. | Смотреть видеоразбор >> |
| 26 | В трапеции ABCD AD=5, BC=2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD. | Смотреть видеоразбор >> |
| 27 | Найдите площадь ромба, если его диагонали равны 4 и 12. | Смотреть видеоразбор >> |
| 28 | Найдите площадь квадрата, если его диагональ равна 1. | Смотреть видеоразбор >> |
| 29 | В прямоугольнике одна сторона равна 33, а диагональ равна 65. Найдите площадь прямоугольника. | Смотреть видеоразбор >> |
| 30 | Основания трапеции равны 10 и 60,одна из боковых сторон равна 1, а синус угла между ней и одним из оснований равен frac{3}{10}. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 31 | В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 32 | Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма. | Смотреть видеоразбор >> |
Задание №18 ОГЭ по математике
Треугольники, четырёхугольники, многоугольники и их элементы
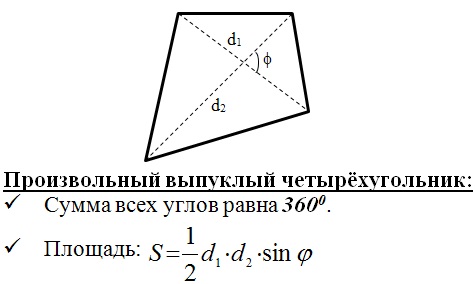
В 18 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства.
В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры.
Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора?
С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить
заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Ответом в задании 16 является целое число или конечная десятичная дробь.
Теория к заданию №18
Приступим к разбору теории.
Выпуклый четырехугольник:
Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:
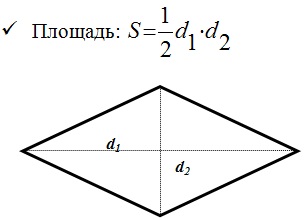
Разберем пример четырехугольника — ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.
Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Ниже я разобрал типовые примеры 11 задания. Давайте приступим к их рассмотрению.
Разбор типовых вариантов задания №18 ОГЭ по математике
Первый вариант задания
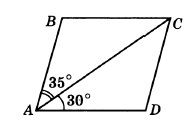
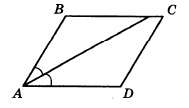
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
Решение:
Найдем угол BAD — это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
∠ABC = ∠ADC = 180 — 65 = 115°
Так как нас просят найти меньший угол, то это 65.
Второй вариант задания
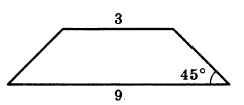
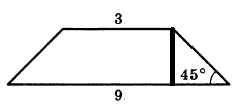
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.
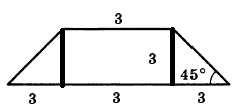
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Третий вариант задания
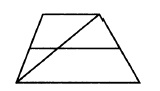
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
Так как нас просят найти больший из отрезков, то ответ 5,5.
Демонстрационный вариант ОГЭ 2019
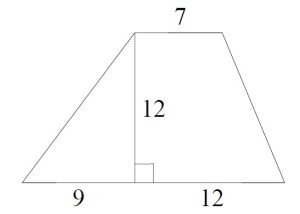
Найдите площадь трапеции, изображённой на рисунке.
Решение:
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это
«полусумма оснований умноженная на высоту»
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²
Четвертый вариант задания
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.
Решение:
Площадь ромба будем искать по формуле:
где a – сторона ромба, h– высота, опущенная на сторону а.
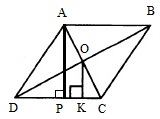
Найдем h. Для этого рассмотрим ∆ОКС и ∆АРС:
Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2.
Пятый вариант задания
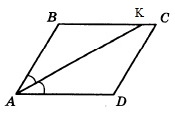
Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 41 0 . Ответ дайте в градусах.
Решение:
Т.к. АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х.
Поскольку АВСD параллелограмм, то ∠В+∠А=180 0 . Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=180 0 –2х.
По теореме о сумме углов треуг-ка ∠ВАК+∠В+∠ВКА=180 0 .
Материал для подготовки к ОГЭ по математике «Площадь треугольника»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Задача 1. В треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите площадь треугольника.
Решение: Площадь треугольника = ½ основания*высоту
Задача 2. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Решение: Пл.прямоугольного треуг. = половине произведения катетов.
Задача 3. Периметр равнобедренного треугольника равен 144, а основание – 64. Найдите площадь треугольника.
1) Т.к. Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ, найдем длину этих сторон:
2) Формула Герона:
Найдем полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
Задача 4. Найдите площадь треугольника.
Решение: Для формулы нам необходимо знать основание и высоту
S треуг.= ½*60*43=1290
Задачу можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем по клеточкам основание =3, высота = 6.
Задачи для самостоятельного решения:
1) В треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите площадь треугольника.
2) Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
3) Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого треугольника.
4) Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр равнобедренного треугольника равен 162, а основание – 72. Найдите площадь треугольника.
6) Найдите площадь треугольника
7) Найдите площадь треугольника

9) Найдите площадь треугольника
10)
11)
12)
13)
14)
16)
Проверить решение можно по ссылке:
Краткое описание документа:
Цель: систематизировать знания учащихся по ключевым разделам планиметрии; создать содержательные и организационные условия для применения школьниками комплекса знаний для решения задач, включаемых в материалы ОГЭ.
В материале по подготовке к ОГЭ приведены алгоритмы решения задач на тему «Площадь треугольника», основные формулы нахождения площади треугольника, задачи для самостоятельного решения, возможность проверки заданий он-лайн.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 99 человек из 45 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 350 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 219 человек из 53 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 532 198 материалов в базе
Другие материалы
- 08.08.2019
- 269
- 0
- 08.08.2019
- 396
- 1
- 08.08.2019
- 217
- 0
- 08.08.2019
- 119
- 0
- 08.08.2019
- 212
- 0
- 08.08.2019
- 259
- 4
- 08.08.2019
- 162
- 0
- 08.08.2019
- 2929
- 11
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 08.08.2019 4111
- DOCX 1.1 мбайт
- 300 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Бутусина Галина Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 8651
- Всего материалов: 6
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минобрнауки учредит стипендию для студентов — победителей международных олимпиад
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Школьники Ленобласти уйдут на внеплановые каникулы
Время чтения: 1 минута
Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников
Время чтения: 1 минута
В Курганской области школьников переведут на дистанционное обучение с 4 февраля
Время чтения: 1 минута
В России планируют создадут сеть центров для подростков «группы риска»
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Площадь треугольника в заданиях ОГЭ
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль «Геометрия» в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ — нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так «площадь треугольника через синус». Итак, посмотрите на чертеж — нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 30 0 . Решение. Используем формулу площади треугольника через синус: Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины — A, B, C. Значит, нам дано: 0 . AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:
В этой задаче мы применили метод приведения для тригонометрических функций.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника — определение площади через высоту. В этой формуле всего нужно знать две величины — основание треугольника и высоту проведенную из вершины треугольника к этому основанию — смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника — высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет — вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы — через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то — в задачах второй части ОГЭ.
http://infourok.ru/material-dlya-podgotovki-k-oge-po-matematike-ploschad-treugolnika-3806698.html
http://repetitor-mathematics.ru/ploshchad-treugolnika-v-zadaniyah-oge/
Площадь треугольника
Задача
1. В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.
Решение: Площадь треугольника = ½
основания*высоту
Пл.треугольника
= ½*27*11=148,5
Ответ:
148,5
Задача
2. Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.
Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.
Пл.прямоуг.треуг.=(4*9):2=36:2=18
Ответ: 18
Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.
Решение:
1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих 
АС=СВ=(144-64):2=40.
2)
Формула Герона:
Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
Ответ: 768
Задача
4. Найдите
площадь треугольника.
Решение: Для формулы нам необходимо
знать основание и высоту
Основание=32+11=43.
Высота
= 60.
S треуг.= ½*60*43=1290
Ответ: 1290
32+11=43
Задача
5.
 |
6
3
Решение:
Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем
по клеточкам основание =3, высота = 6.
S=1/2*3*6= 9
Ответ: 9
Задачи
для самостоятельного решения:
1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.
2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.
3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.
4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.
6) Найдите площадь
треугольника
7) Найдите площадь
треугольника

9) Найдите площадь треугольника
10)
11) 
12)
13)
14)
16)
Проверить решение можно по ссылке:
https://onlinetestpad.com/hnl6ukjjcnpgo
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль “Геометрия” в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ – нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так “площадь треугольника через синус”. Итак, посмотрите на чертеж – нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 300. Решение. Используем формулу площади треугольника через синус: Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины – A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:

Ответ: 1.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника – определение площади через высоту. В этой формуле всего нужно знать две величины – основание треугольника и высоту проведенную из вершины треугольника к этому основанию – смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника – высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет – вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
,
где p – полупериметр треугольника, который находится по формуле:
а, b и c – стороны треугольника.
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы – через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то – в задачах второй части ОГЭ.
































 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.

