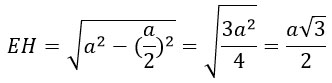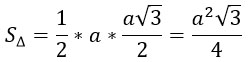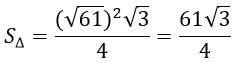Решение:
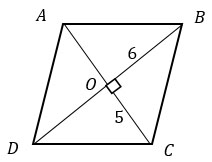
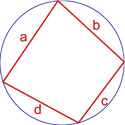
Рассмотрим треугольник ВОС в ромбе ABCD.
Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Это значит, что треугольник ВОС — прямоугольный, а его катеты равны 5 и 6.
По теореме Пифагора найдем гипотенузу ВС.
ВС2 = ОВ2 + ОС2 = 36 + 25 = 61;
ВС = √61.
Если сторона ромба равна √61, то и сторона правильного треугольника KEF равна √61.
Для простоты вычислений выразим формулу площади правильного треугольника. Если ты ее знаешь наизусть – это очень круто!
Условимся, что стороны треугольника EKF равны а.
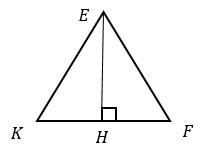
Проведем высоту EH в треугольнике KEF.
Рассмотрим треугольник ЕКН. Он прямоугольный и имеет катеты, равные а и а/2 (т.к. высота является медианой).
Найдем высоту ЕН по теореме Пифагора.
Выразим площадь: она равна половине произведения основанию на высоту, т.е.
Т.к. а = √61, то:
Ответ: 15,25√3 (можно оставить и в дробном виде).
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#758
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
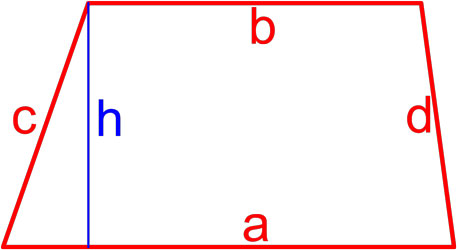
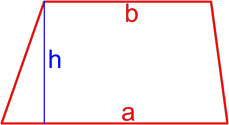
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
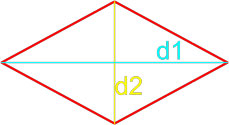
Формула площади ромба через две диагонали:
( S = frac<1>2d_1 d_2 )
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
a — сторона; sin α — синус угла;
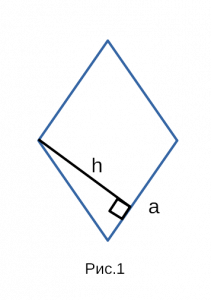
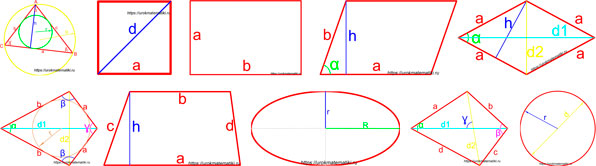
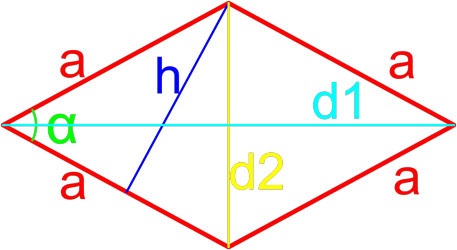
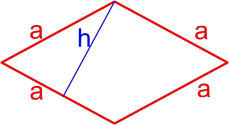
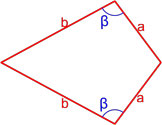
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
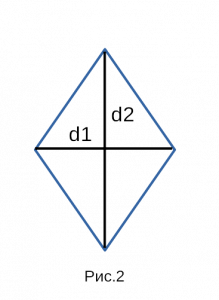
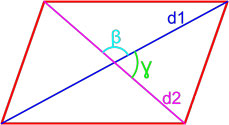
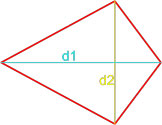
Рис. 2 — площадь ромба через две диагонали
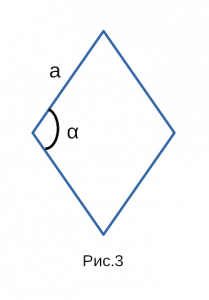
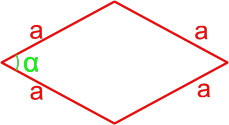
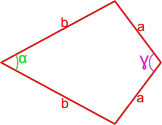
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Площадь ромба
Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.
Площадь ромба по стороне и высоте
Площадь ромба по двум диагоналям
Площадь ромба по углу и противолежащей диагонали
Площадь ромба по углу и диагонали проведенной из этого угла
Площадь ромба по стороне и углу между сторонами
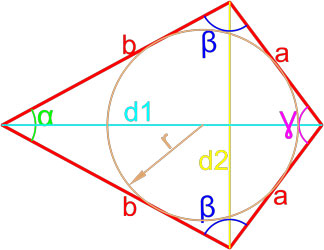
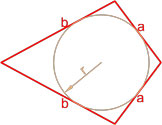
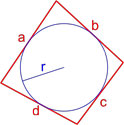
Площадь ромба по радиусу вписанной окружности и углу между сторонами
Площадь ромба по радиусу вписанной окружности и стороне
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула |
| 1 | сторона и высота |  |
| 2 | диагонали | 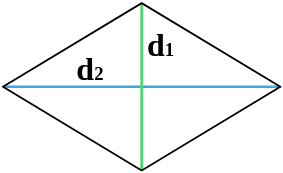 |
| 3 | диагональ и угол между сторонами |  |
| 4 | диагональ и угол между сторонами | 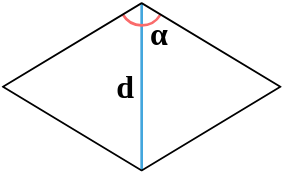 |
| 5 | сторона и угол между сторонами |  |
| 6 | радиус вписанной окружности и угол между сторонами | 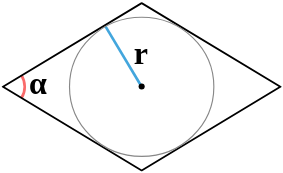 |
| 7 | сторона и радиус вписанной окружности | 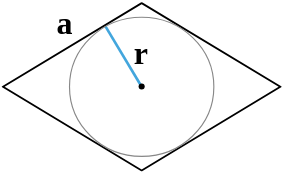 |
Определения
Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Ромб – это частный случай параллелограмма.
Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
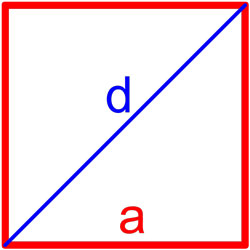
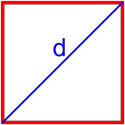
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Формулы площади ромба
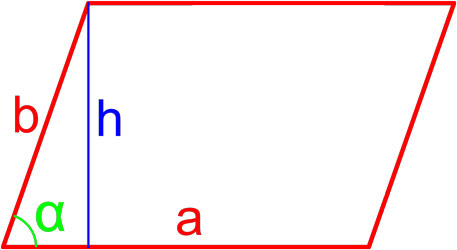
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
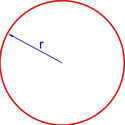
где S — площадь круга,
r — радиус круга.
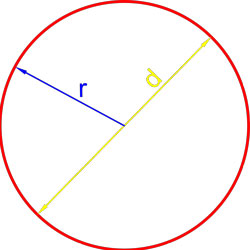
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
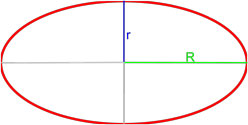
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
http://doza.pro/art/math/geometry/area-rhombus
http://urokmatematiki.ru/reference-information/formuly-po-geometrii/formuly-ploshchadey-figur.php
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 27428 9.1) Найдите площадь правильного…
Условие
slava191
13.05.2018
9.1) Найдите площадь правильного треугольника, сторона которого равна стороне ромба с диагоналями 10 и 12.
математика 10-11 класс
2216
Решение

vk397114329
14.05.2018
★
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Пусть сторона ромба равна a.тогда по теореме Пифагора a^2=25+36=61.
S(тр)=a^2*sgrt(3)/4=(61sgrt(3))/4
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Содержание:
- Формула
- Примеры вычисления площади равностороннего треугольника
Формула
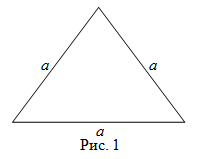
Чтобы найти площадь равностороннего треугольника (рис. 1), нужно квадрат его стороны умножить на
$sqrt{3}$ и поделить на четыре, то есть
$$mathrm{S}_{Delta}=frac{a^{2} sqrt{3}}{4}$$
Эту формулу легко получить из общей
формулы для площади треугольника
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
при условии, что $a=b$ (так как треугольник равносторонний) и
$alpha=60^{circ}$ (угол равностороннего треугольника).
Напомним, что треугольник называется равносторонним, если все его стороны равны.
Примеры вычисления площади равностороннего треугольника
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если известно, что его сторона равна 2 дм.
Решение. Подставив заданное значение в формулу, будем иметь:
$mathrm{S}_{Delta A B C}=frac{2^{2} cdot sqrt{3}}{4}=frac{4 cdot sqrt{3}}{4}=sqrt{3}$ (дм2)
Ответ. $mathrm{S}_{Delta A B C}=sqrt{3}$ (дм2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь равностороннего треугольника
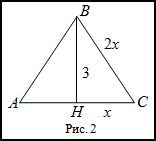
$ABC$, если его высота равна 3 м.
Решение. Сделаем чертеж (рис. 2).
Так треугольник равносторонний, то его высота $BH$ является и
медианой, а это означает, что $AH=HC$ .
Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник
$BHC$. Записываем для него теорему Пифагора:
$$B C^{2}=B H^{2}+H C^{2}$$
$$(2 x)^{2}=2^{2}+x^{2}$$
Решаем полученное уравнение относительно $x$ :
$4 x^{2}-x^{2}=9 Rightarrow 3 x^{2}=9 Rightarrow x^{2}=3 Rightarrow H C=x=sqrt{3}$ (м)
Отсюда получаем, что
$A C=2 x=2 sqrt{3}$ (м)
А тогда искомая площадь
$mathrm{S}_{Delta A B C}=frac{(2 sqrt{3})^{2} cdot sqrt{3}}{4}=frac{12 sqrt{3}}{4}=3 sqrt{3}$ (м2)
Ответ. $mathrm{S}_{Delta A B C}=3 sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными
сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² — (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно,
что площадь треугольной фигуры, отсекаемой от него средней линией,
составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим
длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим
как МК. Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее
равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что
его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на
3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а
высоту, проведенную к ней, — как h, то формула расчета площади этой фигуры
будет выглядеть так:
S=ah/2.
Принимая во внимание то, что все стороны данной треугольной фигуры равны,
то его высоту можно выразить через сторону и вычислить, используя теорему
Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего
треугольника?
Для расчета площади треугольника, длины всех сторон которого равны,
используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего
треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то
его площадь рассчитывается так:
S = а²√3/4.
Каким образом можно привести доказательство теоремы о площади
равностороннего треугольника?
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой
одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его
углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит
квадрат на 2 равные части. Из этого следует, что площадь треугольника
равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из
сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной
6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет
собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего
треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно,
если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь
которого равна произведению длины стороны и высоты.
Параллелограмм состоит из двух треугольников, которые равны. Это значит,
что площадь одной из треугольных фигур находится так:
S = a*h /2.
Высоту можно выразить через определение синуса.
Все углы в равносторонней треугольной фигуре равны и составляют 60
градусов (180/3).
sin(60) = V3/2.
Из определения синуса следует:
h/a = sin(60).
Это значит, что:
h = a*V3/2.
Значит:
S = a*a*V3/4.
Почему площадь равностороннего треугольника равна a^2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный
ими, — как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60
градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если
подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой
его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус
круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры,
равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как
вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр
окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около
него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота =
14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что
каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии,
что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3.
Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от
его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой
описанной около нее окружности. Ее радиус представляет собой расстояние от
центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60
градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона
имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь
в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине
стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь
вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон
одинаковые. Исходя из этого можно найти его сторону, разделив периметр на
три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность,
которая вписана в него, имеет радиус длиной 4 см.?
Площадь треугольника, имеющего стороны одинаковой длины, может быть
рассчитана через длину его стороны без применения формулы радиуса
окружности, которая вписана в него. Для данной фигуры верно утверждение о
том, что высота, биссектриса и медиана делятся в точке пересечения в
отношении 2:1. При схематичном изображении можно увидеть, что треугольная
фигура АВС включает 6 треугольников с прямыми углами, которые имеют
одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь
треугольника АВС будет представлять собой сумму площадей всех 6
треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной
а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то
его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами,
зная формулу, по которой вычисляется площадь равностороннего треугольника
(S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади
равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов.
Также известна формула вычисления площади данной фигуры путем умножения
длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если
известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а,
то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также
представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина
которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой
также медиану, делящую на две равные части сторону, на которую она
опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает
площадь другого в три раза. Чему будет равна сторона второго равностороннего
треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.кв.
Известно, что площадь второго треугольника больше площади первой фигуры в
три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его
площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.