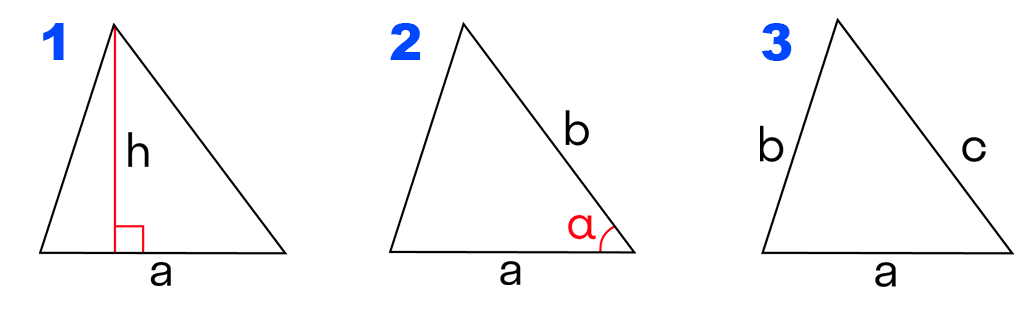
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
Основание треугольника:
a =
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
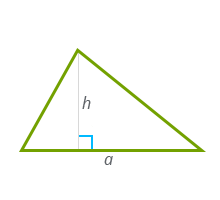
1) через основание и высоту
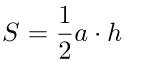
a – основание треугольника,
h – высота треугольника.
2) через две стороны и угол
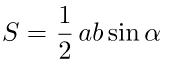
a, b – стороны треугольника,
α – угол между сторонами.
3) По трем сторонам. Формула Герона.
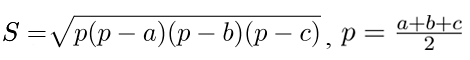
a, b, с – стороны треугольника,
p – полупериметр треугольника.
4) Через радиус вписанной окружности.
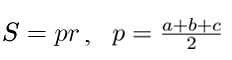
a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
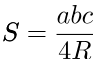
a, b, с – стороны треугольника,
R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
как найти площадь прямоугольного треугольника
Как найти площадь треугольника, как найти площадь прямоугольного треугольника. Формула нахождения площади треугольника.
Всё о площади треугольника.
- Формула площади треугольника
- Пример/задача нахождения площади треугольника
- Найти площадь треугольника онлайн
- Найти площадь треугольника если известна сторона и диагональ
- Найти площадь треугольника онлайн, если известна диагональ и сторона
Формула площади треугольника
Когда мы говорим о формуле площади треугольника, то подразумеваем, что это прямоугольный треугольник(просто… так уж сложилось по умолчанию) :
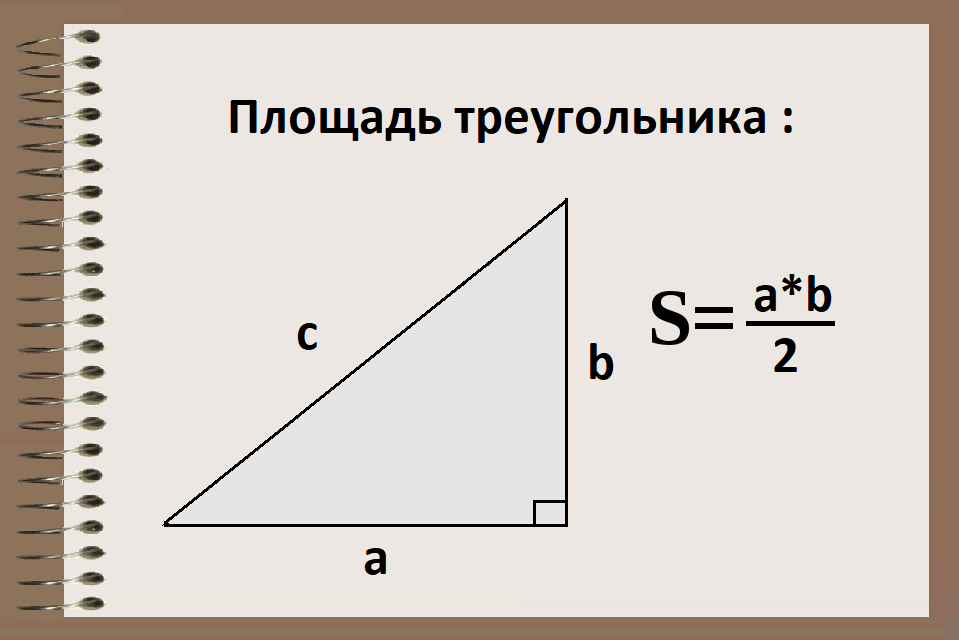
S = a*b/2
Где S — площадь (единица измерения)²
a — длина одной из сторон.
b — длина второй стороны.
Иногда, данная формула не подходит к тому или иному виду треугольников!
Еще смотри — всё о треугольниках
Пример/задача нахождения площади треугольника
Условие задачи :
Требуется найти площадь прямоугольного треугольника. Известно, что один из катетов равен 15см(сторона а). Второй катет равен 8см(сторона b).
Первым шагом, при решении задачи о площади треугольника — требуется узнать вид треугольника, потому. что площадь разных треугольников высчитывается по разному! Здесь мы видим. что в задаче указано, какой подвид треугольника —
прямоугольный
И далее нам нужно взять формулу площади треугольника и подставить в неё все известные параметры.
S =a*b2
a = 15см, и = 8см
S = 15*82 = 1202 = 60см²
Результат данной задачи вы можете проверить в ниже идущем пункте.
Найти площадь треугольника онлайн
Если известно у прямоугольного треугольника сторона «а» и сторона «b», то для такого треугольника мы можем посчитать площадь онлайн.
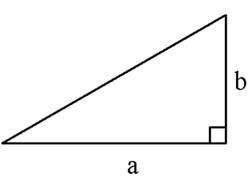
Для того, чтобы посчитать площадь прямоугольного треугольника онлайн, вам требуется в поле :
Первая сторона — заполнить значением первой стороны.
Вторая сторона — заполнить значением второй стороны.
И нажать кнопку посчитать.
Найти площадь треугольника если известна сторона и диагональ
Условие задачи :
Найти площадь прямоугольного треугольника, если диагональ «c» = 10см. Одна сторона равно 8см.
Для нахождения длины неизвестной стороны, нам понадобится «теорема пифагора». Обозначим неизвестную сторону через «х»
Составляем уравнение : с² = а² +
х
²
Выводим х :
х
=
√
с² — а²
Подставляем данные нашей задачи :
х
=
√
10² — 8² =
√
100 — 64 =
√
36 = 6
После того, как мы нашли недостающую сторону. мы можем найти площадь прямоугольного треугольника по формуле ,
где : b = х
S =a*b2
Подставляем наши данные в формулу:
S = 8 * 62 = 482 = 24см²
Найти площадь треугольника онлайн, если известна диагональ и сторона
Для нахождения неизвестной стороны в прямоугольном треугольнике, написали скрипт, который может посчитать это.
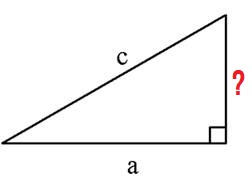
Для того, чтобы найти длину неизвестной стороны и площадь данного прямоугольного треугольника… в поле ввода введите:
В первом поле длину стороны.
Во втором поле введите длину гипотенузы.
Не благодарите, но ссылкой можете поделиться!
COMMENTS+
BBcode
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
📐 Когда нужно знать площадь треугольника?
Знание площади треугольника может быть полезно во многих сферах жизни, включая математику, науки, строительство, дизайн и другие области.
Вот некоторые конкретные примеры, когда необходимо знать площадь треугольника:
- В математике – для решения задач на нахождение площади треугольника или расчета других параметров на основе площади.
- В науках – для расчета площади треугольной формы в различных контекстах, например, при изучении геометрии или физики.
- В строительстве – для расчета площади треугольного участка поверхности, например, для закупки материалов или расчета стоимости работ.
- В дизайне – для расчета площади треугольных участков земли или других поверхностей, например, для планировки ландшафта или выбора размера ковра.
- В повседневной жизни – для решения различных задач, например, для расчета площади треугольной поверхности мебели или для оценки площади треугольного участка земли в саду.
Знание площади треугольника может быть полезным во многих ситуациях, где треугольная форма играет важную роль, и поможет справиться с различными задачами более эффективно.
Как рассчитывается площадь треугольника?
Площадь треугольника может быть рассчитана на основе формулы, зависящей от известных параметров треугольника. Существуют несколько различных формул для расчета площади треугольника, которые можно использовать в зависимости от того, какие параметры известны.
Формула 1. Через длину основания и высоту, опущенную на это основание:
S = a × h/2
Формула 2. Через две стороны и угол между ними:
S = 1/2 × a × b × sin α
где α — угол между сторонами а и b
Формула 3. Формула Герона через 3 стороны:
S = √ [p × (p-a) × (p-b) × (p-c)]
где p = (a+b+c)/2 – полупериметр.
Во всех формулах S обозначает площадь треугольника, b обозначает длину основания прямоугольного треугольника, h обозначает высоту, a, b, и c обозначают длины сторон непрямоугольного треугольника, x и y обозначают координаты вершин треугольника.
Рассчитывая площадь треугольника, важно использовать правильную формулу в зависимости от известных параметров, чтобы получить правильный ответ.
Что такое калькулятор площади треугольника?
Калькулятор площади треугольника – это онлайн-инструмент, который позволяет быстро и легко рассчитать площадь треугольника на основе известных параметров. Обычно для расчета площади треугольника в калькуляторе необходимо ввести значения одного или нескольких параметров, таких как длина основания и высота прямоугольного треугольника, длины всех трех сторон непрямоугольного треугольника или координаты вершин треугольника на координатной плоскости.
Калькулятор площади треугольника может быть полезен во многих ситуациях, например, при проектировании строительных конструкций, расчете площадей полей и участков земли, а также при решении математических задач в школе или вузе. Благодаря калькулятору площади треугольника можно быстро получить точный результат, избегая ошибок, которые могут возникнуть при ручных расчетах.
Как работает калькулятор площади треугольника?
Работа калькулятора площади треугольника может немного отличаться в зависимости от конкретного онлайн-инструмента, но обычно он использует формулу для расчета площади треугольника на основе заданных параметров.
Если треугольник является прямоугольным, то для расчета его площади необходимо знать длину основания и высоту, которая опускается на это основание. А если треугольник непрямоугольный, то для расчета его площади необходимо знать длины всех трех сторон.
Калькулятор площади треугольника может использовать эти формулы для расчета площади, если пользователь введет необходимые параметры (например, длины сторон или длину основания и высоту). Результат может быть выдан в виде числа или дроби в зависимости от точности калькулятора.
Как использовать калькулятор?
Использовать калькулятор площади треугольника довольно просто. Вот общие шаги, которые необходимо выполнить для использования калькулятора:
- Откройте калькулятор площади треугольника в своем браузере. Вы можете найти онлайн-калькуляторы площади треугольника на многих сайтах, которые предоставляют подобные сервисы, в том числе и на нашем.
- Введите параметры треугольника, которые известны вам. В зависимости от конкретного калькулятора вы можете вводить длины сторон, длину основания и высоту, координаты вершин на плоскости и т.д.
- Нажмите на кнопку «Рассчитать» или «Вычислить». Калькулятор площади треугольника обычно автоматически рассчитывает площадь на основе введенных параметров и выдает результат.
- Прочитайте результат. Калькулятор площади треугольника может выдавать результат в разных форматах, например, в виде числа или дроби. Если вы хотите, чтобы результат был точнее, можете использовать калькулятор с более высокой точностью.
- Сбросьте введенные данные и повторите расчет, если нужно. Если вам нужно рассчитать площадь треугольника с другими параметрами, то можете сбросить предыдущие данные и ввести новые параметры.
В целом, использование калькулятора площади треугольника довольно просто и позволяет быстро и точно рассчитать площадь треугольника на основе его параметров.
❓Вопросы и ответы
Также полезно ознакомиться с ответами на часто задаваемые вопросы по данному вопросу.
Как использовать калькулятор площади треугольника?
Для использования калькулятора площади треугольника нужно ввести известные параметры треугольника, такие как длины сторон, длина основания и высота, координаты вершин на плоскости и т.д., а затем нажать на кнопку «Рассчитать» или «Вычислить». Калькулятор автоматически рассчитывает площадь треугольника и выводит результат.
Какой формулой рассчитывается площадь треугольника?
Площадь треугольника можно рассчитать с помощью формулы: S = (a * h) / 2, где S – площадь треугольника, a – длина основания, h – высота, опущенная на основание.
Где можно найти онлайн-калькулятор площади треугольника?
Онлайн-калькуляторы площади треугольника можно найти на многих сайтах, которые предоставляют подобные сервисы. Также можно использовать калькуляторы научных порталов или мобильные приложения.
Какие единицы измерения используются в калькуляторе площади треугольника?
Калькулятор площади треугольника может использовать разные единицы измерения, например, метры, сантиметры, дюймы, футы и т.д. Обычно единицы измерения выбираются в соответствии с системой измерений, используемой в конкретной стране или регионе.
Можно ли использовать калькулятор площади треугольника для расчета площади других фигур?
Нет, калькулятор площади треугольника предназначен только для расчета площади треугольников. Для расчета площади других геометрических фигур необходимо использовать другие калькуляторы, например, калькуляторы площади круга, прямоугольника и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Треугольник — это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.
Онлайн-калькулятор площади треугольника
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по основанию и высоте
S=12⋅a⋅hS= frac{1}{2}cdot acdot h,
aa — основание треугольника;
hh — высота треугольника, проведенная к данному основанию a.
Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в формулу для площади и получаем:
S=12⋅10⋅5=25S=frac{1}{2}cdot10cdot 5=25 (см. кв.)
Ответ: 25 (см. кв.)
Формула площади треугольника по длинам всех сторон
S=p⋅(p−a)⋅(p−b)⋅(p−c)S= sqrt{pcdot(p-a)cdot (p-b)cdot (p-c)},
a,b,ca, b, c — длины сторон треугольника;
pp — половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
p=12(a+b+c)p=frac{1}{2}(a+b+c)
Эта формула называется формулой Герона.
Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
Найдем половину периметра pp:
p=12(3+4+5)=12⋅12=6p=frac{1}{2}(3+4+5)=frac{1}{2}cdot 12=6
Тогда, по формуле Герона, площадь треугольника:
S=6⋅(6−3)⋅(6−4)⋅(6−5)=36=6S=sqrt{6cdot(6-3)cdot(6-4)cdot(6-5)}=sqrt{36}=6 (см. кв.)
Ответ: 6 (см. кв.)
Формула площади треугольника по одной стороне и двум углам
S=a22⋅sinβsinγsin(β+γ)S=frac{a^2}{2}cdot frac{sin{beta}sin{gamma}}{sin(beta+gamma)},
aa — длина стороны треугольника;
β,γbeta, gamma — углы, прилежащие к стороне aa.
Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.
Решение
a=10a=10
β=30∘beta=30^{circ}
γ=30∘gamma=30^{circ}
По формуле:
S=1022⋅sin30∘sin30∘sin(30∘+30∘)=50⋅123≈14.4S=frac{10^2}{2}cdot frac{sin{30^{circ}}sin{30^{circ}}}{sin(30^{circ}+30^{circ})}=50cdotfrac{1}{2sqrt{3}}approx14.4 (см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a⋅b⋅c4RS=frac{acdot bcdot c}{4R},
a,b,ca, b, c — стороны треугольника;
RR — радиус описанной окружности вокруг треугольника.
Числа возьмем из второй нашей задачи и добавим к ним радиус RR окружности. Пусть он будет равен 10 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
R=10R=10
S=3⋅4⋅54⋅10=6040=1.5S=frac{3cdot 4cdot 5}{4cdot 10}=frac{60}{40}=1.5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S=p⋅rS=pcdot r,
pp — половина периметра треугольника:
p=a+b+c2p=frac{a+b+c}{2},
a,b,ca, b, c — стороны треугольника;
rr — радиус вписанной в треугольник окружности.
Пусть радиус вписанной окружности равен 2 (см.). Длины сторон возьмем из предыдущей задачи.
Решение
a=3a=3
b=4b=4
c=5c=5
r=2r=2
p=3+4+52=6p=frac{3+4+5}{2}=6
S=6⋅2=12S=6cdot 2=12 (см. кв.)
Ответ: 12 (см. кв.)
Формула площади треугольника по двум сторонам и углу между ними
S=12⋅b⋅c⋅sin(α)S=frac{1}{2}cdot bcdot ccdotsin(alpha),
b,cb, c — стороны треугольника;
αalpha — угол между сторонами bb и cc.
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b=5b=5
c=6c=6
α=30∘alpha=30^{circ}
S=12⋅5⋅6⋅sin(30∘)=7.5S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!