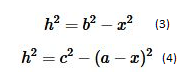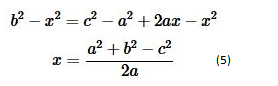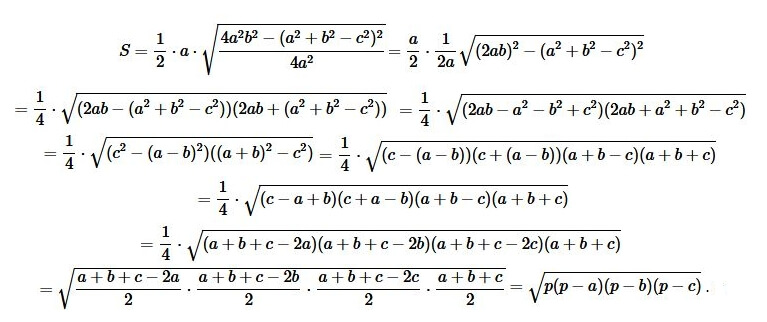Площадь треугольника S (в кв.м.) можно вычислить по формуле
Формулировка задачи: Площадь треугольника S (в кв.м.) можно вычислить по формуле S = 1/2 ⋅ a ⋅ h, где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону a, если даны площадь треугольника и высота h.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4 (Преобразование выражений).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Площадь треугольника S (в кв.м.) можно вычислить по формуле S = 1/2 ⋅ a ⋅ h, где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону a, если площадь треугольника равна 28 кв.м., а высота h равна 14 м.
Выразим сторону a из формулы. Чтобы найти неизвестный множитель, нужно разделить произведение на известный множитель:
a = S / (1/2 ⋅ h) = 2S / h
Подставим известные данные в формулу и получим результат:
a = 2 ⋅ 28 / 14 = 56 / 14 = 4
В общем виде решение данной задачи выглядит следующим образом:
Осталось лишь подставить конкретные значения и получить ответ.
Поделитесь статьей с одноклассниками «Площадь треугольника S (в кв.м.) можно вычислить по формуле – как решать».
Есть другой способ решения?
Предложите другой способ решения задачи «Площадь треугольника S (в кв.м.) можно вычислить по формуле». Возможно, он окажется более понятным для кого-нибудь:
Площадь треугольника S (в м2) можно вычислить по формуле S = 1 / 2ah, где a — сторона треугольника , h — высота, проведенная к этой стороне (в метрах)?
Математика | 5 — 9 классы
Площадь треугольника S (в м2) можно вычислить по формуле S = 1 / 2ah, где a — сторона треугольника , h — высота, проведенная к этой стороне (в метрах).
Пользуясь этой формулой, найдите сторону a, если площадь треугольника равна 28м2 , а высота h равна 14м.
28 = 1 / 2 * a * 14
Разделим на 14 обе части
Умножим на 2 обе части
2 * 2 = 1 / 2 * 2 * а
Ответ : Сторона равна 4 метрам.
Найти площадь треугольника со сторонами 5?
Найти площадь треугольника со сторонами 5.
Помогите решить?
Лист бумаги квадратной формы со стороной 8 см разрезали на четыре равных треугольника.
Найди площадь одного треугольника.
Помогите пожалуйста?
Периметр треугольника равен 27 см.
Длины сторон треугольника относятся как 2 : 3 : 4.
Найдите длины сторон треугольника.
Покакой формуле вычислить площадь и периметр треугольника?
Покакой формуле вычислить площадь и периметр треугольника.
Пожалуйста решите задачу : из куска проволки сначала сделали треугольник, а затем пятиугольник с равными сторонам Найди длину стороны пятиугольника?
Пожалуйста решите задачу : из куска проволки сначала сделали треугольник, а затем пятиугольник с равными сторонам Найди длину стороны пятиугольника.
Медиана равностороннего треугольника равна 9 корней из 3 ?
Медиана равностороннего треугольника равна 9 корней из 3 .
Найдите его сторону.
Сторона квадрата равно 0?
Сторона квадрата равно 0.
4дм. Найдите сторону квадрата, площадь которого составляет 0.
25 площади данного квадрата.
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33?
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33.
Найдите площадь треугольника.
Одна из сторон равнобедренного треугольника равна 4 см, найдите две другие стороны, если периметр треугольника равен 14 см?
Одна из сторон равнобедренного треугольника равна 4 см, найдите две другие стороны, если периметр треугольника равен 14 см.
Перемитр треугольника если длина одной стороны равна 7см, длина второй13см, а третья сторона короче на3см?
Перемитр треугольника если длина одной стороны равна 7см, длина второй13см, а третья сторона короче на3см.
На этой странице вы найдете ответ на вопрос Площадь треугольника S (в м2) можно вычислить по формуле S = 1 / 2ah, где a — сторона треугольника , h — высота, проведенная к этой стороне (в метрах)?. Вопрос соответствует категории Математика и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.
1) 18 + 3 = 21 км / ч — скорость по течению 2) 21 км / ч * 3, 5 ч = 73, 5 км — расстояние.
Если я верно понял задачу то нам в принципе не важно, где лежит начало вектора. Важно, чтобы конец вектора лежал на параболе. Координата «y» (игрек) конца вектора известна — — 9. Найдем координаты «х» (икс) из уравнения параболы .
Ответ на фотооооооооооооооо.
Надо разделить число на десятки и единицы на пример 27 + 32 = 59 30 2.
12 * 2 = 24(колеса)если бы все были двухколесные 27 — 25 = 3(велосипеда)трехколесные 12 — 3 = 9(велосипедов)двухколесные.
НОК(185 и 451) = 1 То есть числа 185 и 451 — взаимно простые.
451 = 11 · 41 185 = 5 · 37 НОК (185 ; 451) = 11 · 41 · 5 · 37 = 83435 Наименьшее общее кратное НОК (185 ; 451) = 83435.
1) 27 : 3 = 9 2) 45 + 9 = 54 3) 54 — 12 = 42 Ответ : 42.
15×4 = 60(коп) потратила Маша на сообщения 8 рублей = 800копеек 800 — 60 = 760(коп) осталось 760коп = 7руб 40 коп.
Формула площади.
Формула площади необходима для определения площадь фигуры, которая является вещественнозначной функцией, определённой на некотором классе фигур евклидовой плоскости и удовлетворяющая 4м условиям:
- Положительность — Площадь не может быть меньше нуля;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения 2х фигур без общих внутренних точек равна сумме площадей этих фигур.
Результат сложения расстояний между серединами противоположных сторон выпуклого четырехугольника будут равна его полупериметру.
Сектор круга.
Площадь сектора круга равна произведению его дуги на половину радиуса.
Сегмент круга.
Чтобы получить площадь сегмента ASB, достаточно из площади сектора AOB вычесть площадь треугольника AOB.
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
Эллипс.
Еще один вариант как вычислить площадь эллипса – через два его радиуса.
Треугольник. Через основание и высоту.
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
Треугольник. Через две стороны и угол.
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.
Треугольник. Формула Герона.
Площадь треугольника можно определить при помощи формулы Герона.
Треугольник. Через радиус вписанной окружности.
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Треугольник. Через радиус описанной окружности.
Площадь треугольника можно определить по радиусу описанной окружности.
Треугольник.
Площадь прямоугольного треугольника.
Треугольник.
Площадь прямоугольного треугольника через вписанную окружность.
Треугольник.
Формула Герона для прямоугольного треугольника.
Треугольник.
Площадь равнобедренного треугольника.
Трапеция.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Ромб. По длине стороны и высоте.
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Ромб. По длине стороны и углу.
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Ромб.
Формула площади ромба по длинам его диагоналей.
Формула площади круга через его радиус и диаметр.
Квадрат. Через его сторону.
Площадь квадрата равна квадрату длины его стороны.
Квадрат. Через его диагонали.
Площадь квадрата равна половине квадрата длины его диагонали.
Правильный многоугольник.
Для определения площади правильного многоугольника необходимо разбить его на равные треугольники, которые бы имели общую вершину в центре вписанной окружности.
Сфера.
Площадь поверхности сферы равна учетверенной площади большого круга.
Куб.
Площадь поверхности куба равна сумме площадей шести его граней.
Конус.
Боковая площадь поверхности круглого конуса равна произведению половины окружности основания (C) на образующую (l).
S = 1/2 C * l = π r l
Усеченный конус.
Боковая площадь поверхности усеченного конуса.
Цилиндр.
Площадь боковой поверхности круглого цилиндра.
Сегмент шара.
Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.
Поверхность шарового слоя.
Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара.
http://matematika.my-dict.ru/q/990304_plosad-treugolnika-s-v-m2-mozno/
http://www.calc.ru/Formula-Ploshchadi.html?print=1
| Геометрическая фигура | Формула | Чертеж |
|---|---|---|
Формулы площади геометрических фигур.
|
Площадь треугольника можно вычислить по формуле S=1/2 ah, где а — сторона треугольника, h — высота, проведенная к этой стороне. Пользуясь этой формулой, найдите сторону а, если площадь треугольника равна 28, а высота h равна 14. Итак, по условию нам даны следующие измерения: S = 28 h = 14 а = ? Преобразуем формулу площади треугольника следующим образом: 28 = 14а/2; упростим вторую часть нашего уравнения: 28 = 7а; Далее методом решения просто уравнения с одной переменной найдем а, для этого нам нужно обе части нашего уравнения разделить на 7. Таким образом, а = 4 Ответ: сторона треугольника равна 4 автор вопроса выбрал этот ответ лучшим Aleh2022 4 месяца назад По условию задачи: S=28 сантиметров квадратных /площадь треугольника/ h=14 сантиметров /высота к стороне a/ Площадь треугольника вычисляется по формуле: S=0.5 * a * h Отсюда находим a=28 / 14 / 0.5 = 4 В результате получаем: a = 4 сантиметра Знаете ответ? |
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Понятие площади
Определение
Площадью (S) геометрической фигуры именуется численная величина, характеризующая её размер.
В этом собственно и состоит понятие площади. У неё есть следующие два свойства:
- Площадь равных геометрических фигур имеет одно и то же числовое значение;
- Величина площади фигуры равняется сумме единичных площадей квадратов, на которые её можно разделить.
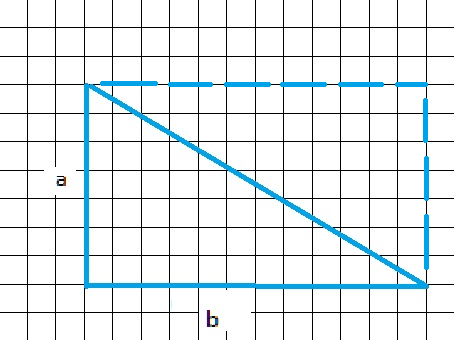
Пример 1.
Пусть у нас имеется прямоугольник в котором укладывается 7 клеток по вертикали и 12 по горизонтали. Это значит он будет иметь стороны a=7 и b=12.
Из рисунка видно, что S нашего треугольника это половина таковой у прямоугольника. Последняя вычисляется так [mathrm{S}_{text {прям }}=mathrm{a} * mathrm{~b}]. Чтобы узнать площадь треугольника, разделим [mathrm{S}_{text {прям }}] на 2, тогда получим:
Формула 1
[S= (a*b)/2].
Подставляем численные значения (7*12)/2 = 42.
Как найти площадь треугольника, если мы знаем его основание и высоту
Теорема
Площадь любого треугольника численно равняется половине произведения длины основания на высоту фигуры.
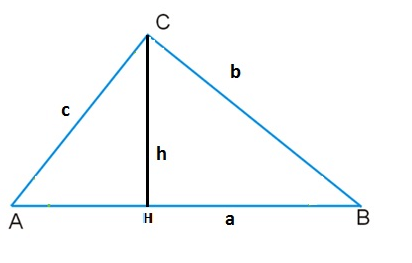
В нашем случае основанием считается сторона AB. Формула для S получается следующей:
Формула 2
[S=(1/2)*AB*h ].
Доказательство:
Посмотрите рисунок. Из него ясно видно, что высота h делит ABC на 2 прямоугольных треугольника ACH и HCB.
По формуле (1) вычисление S каждого из них идёт так.
S(ACH) = (1/2)(AH)*h
S(HCB)=(1/2)(HB)*h
Чтобы вычислить площадь треугольника abc, нужно S(ACH) и S(HCB) сложить.
S=(1/2)(AH)*h+ (1/2)(HB)*h
Выносим (1/2) и h за скобки и получаем
(1/2)*h*(AH+HB)
Но AH+HB=AB, т. е.
S = (1/2)*AB*h, что и требовалось доказать.
Как видите, формулу площади треугольника получить и доказать достаточно легко.
Теперь о том, как найти площадь треугольника прибегнув к формуле Герона. Эта задача тоже не особо трудная.
Нет времени решать самому?
Наши эксперты помогут!
Формула Герона для треугольника
По формуле Герона S треугольника, имеющего стороны a, b, c равна:
[S=sqrt{p(p-a)(p-b)(p-c)}]
P — полупериметр. Он равен
[p=frac{a+b+c}{2}]
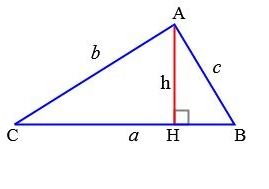
Доказательство:
Положим, что x=CH. В этом случае BH=a-x
С помощью теоремы Пифагора по отношению к AHC и AHB будем иметь
Из них следует, что
[b^{2}-x^{2}=c^{2}-(a-x)^{2}]
Отсюда легко найти
Чтобы найти h подставляем (5) в (3) и получаем
[h=sqrt{b^{2}-x^{2}}=sqrt{b^{2}-left(frac{a^{2}+b^{2}-c^{2}}{2 a}right)^{2}}] (6)
Тогда S будет равняться
[S=frac{1}{2} cdot a cdot h=frac{1}{2} cdot a cdot sqrt{b^{2}-left(frac{a^{2}+b^{2}-c^{2}}{2 a}right)^{2}}] (7)
Преобразовав это выражение, получаем формулу Герона для площади треугольника.
Вот так можно найти площадь треугольника по формуле Герона.
Площадь равностороннего треугольника
Формула
Площадь равностороннего треугольника можно вычислить по формуле:
[S=frac{alpha^{2} sqrt{3}}{4}].
где a —длина одной из трёх сторон.
Для её доказательства употребим формулу Герона.
Полупериметр в нашем случае равен
p = (З/2)*a
Выражение под знаком корня в формуле Герона можно записать в виде
[sqrt{p^{*}(p-a)^{2 *}(p-a)}]
Выносим второй член произведения из-под корня и получаем
[(p-a) sqrt{p^{*}(p-a)}]
Далее так как p-a = (За-2а)/2=a/2 формула Герона для треугольника приобретает следующий вид
[mathrm{S}=mathrm{a} / 2 sqrt{(3 / 4)^{*} mathrm{a}^{2}}]
Выносим из-под корня a2 и 4 в знаменателе, в результате расчёта получаем
[S=frac{alpha^{2} sqrt{3}}{4}]
Что и требовалось доказать.
Треугольник — это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.
Онлайн-калькулятор площади треугольника
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по основанию и высоте
S=12⋅a⋅hS= frac{1}{2}cdot acdot h,
aa — основание треугольника;
hh — высота треугольника, проведенная к данному основанию a.
Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в формулу для площади и получаем:
S=12⋅10⋅5=25S=frac{1}{2}cdot10cdot 5=25 (см. кв.)
Ответ: 25 (см. кв.)
Формула площади треугольника по длинам всех сторон
S=p⋅(p−a)⋅(p−b)⋅(p−c)S= sqrt{pcdot(p-a)cdot (p-b)cdot (p-c)},
a,b,ca, b, c — длины сторон треугольника;
pp — половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
p=12(a+b+c)p=frac{1}{2}(a+b+c)
Эта формула называется формулой Герона.
Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
Найдем половину периметра pp:
p=12(3+4+5)=12⋅12=6p=frac{1}{2}(3+4+5)=frac{1}{2}cdot 12=6
Тогда, по формуле Герона, площадь треугольника:
S=6⋅(6−3)⋅(6−4)⋅(6−5)=36=6S=sqrt{6cdot(6-3)cdot(6-4)cdot(6-5)}=sqrt{36}=6 (см. кв.)
Ответ: 6 (см. кв.)
Формула площади треугольника по одной стороне и двум углам
S=a22⋅sinβsinγsin(β+γ)S=frac{a^2}{2}cdot frac{sin{beta}sin{gamma}}{sin(beta+gamma)},
aa — длина стороны треугольника;
β,γbeta, gamma — углы, прилежащие к стороне aa.
Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.
Решение
a=10a=10
β=30∘beta=30^{circ}
γ=30∘gamma=30^{circ}
По формуле:
S=1022⋅sin30∘sin30∘sin(30∘+30∘)=50⋅123≈14.4S=frac{10^2}{2}cdot frac{sin{30^{circ}}sin{30^{circ}}}{sin(30^{circ}+30^{circ})}=50cdotfrac{1}{2sqrt{3}}approx14.4 (см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a⋅b⋅c4RS=frac{acdot bcdot c}{4R},
a,b,ca, b, c — стороны треугольника;
RR — радиус описанной окружности вокруг треугольника.
Числа возьмем из второй нашей задачи и добавим к ним радиус RR окружности. Пусть он будет равен 10 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
R=10R=10
S=3⋅4⋅54⋅10=6040=1.5S=frac{3cdot 4cdot 5}{4cdot 10}=frac{60}{40}=1.5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S=p⋅rS=pcdot r,
pp — половина периметра треугольника:
p=a+b+c2p=frac{a+b+c}{2},
a,b,ca, b, c — стороны треугольника;
rr — радиус вписанной в треугольник окружности.
Пусть радиус вписанной окружности равен 2 (см.). Длины сторон возьмем из предыдущей задачи.
Решение
a=3a=3
b=4b=4
c=5c=5
r=2r=2
p=3+4+52=6p=frac{3+4+5}{2}=6
S=6⋅2=12S=6cdot 2=12 (см. кв.)
Ответ: 12 (см. кв.)
Формула площади треугольника по двум сторонам и углу между ними
S=12⋅b⋅c⋅sin(α)S=frac{1}{2}cdot bcdot ccdotsin(alpha),
b,cb, c — стороны треугольника;
αalpha — угол между сторонами bb и cc.
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b=5b=5
c=6c=6
α=30∘alpha=30^{circ}
S=12⋅5⋅6⋅sin(30∘)=7.5S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!