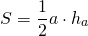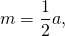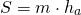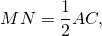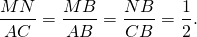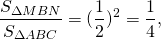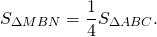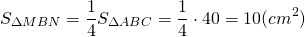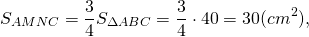На чтение 4 мин Просмотров 2.2к. Опубликовано 04.07.2019
Содержание
- Содержание
- Средняя линия треугольника [ править | править код ]
- Свойства [ править | править код ]
- Признаки [ править | править код ]
- Средняя линия четырёхугольника [ править | править код ]
- Свойства [ править | править код ]
- Средняя линия трапеции [ править | править код ]
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Содержание
Средняя линия треугольника [ править | править код ]
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника [1] .
Свойства [ править | править код ]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки [ править | править код ]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника [ править | править код ]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства [ править | править код ]
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции [ править | править код ]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 <displaystyle EF=<frac <2>>> 
07.06.2019 
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Площадь треугольника ABC равна 176, DE — средняя линия. Найдите площадь треугольника CDE.
Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Выясним, как связаны средняя линия треугольника и его площадь.

Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.

Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
Выясним, как связаны средняя линия треугольника и его площадь.

Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Вывод:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.

Поскольку
то
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
то есть
Вывод:
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
Средняя линия треугольника и его площадь
Выясним, как связаны средняя линия треугольника и его площадь.
I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.
Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
Как найти среднюю линию треугольника?
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
http://skysmart.ru/articles/mathematic/kak-najti-srednyuyu-liniyu-treugolnika
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` — углы треугольника`ABC`; `a`, `b` и `c` — противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` — высоты к этим сторонам; `r` — радиус вписанной окружности;`R` — радиус описанной окружности; `2p=(a+b+c)` — периметр треугольника; `S` — площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` — формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь — найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` — точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` — середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL«||«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«||«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«||«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` — точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` — площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` — середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` — точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,