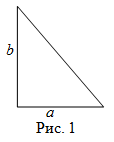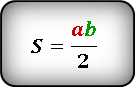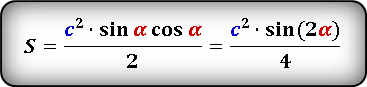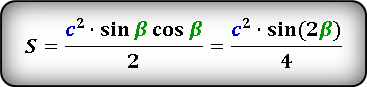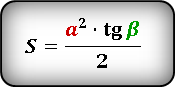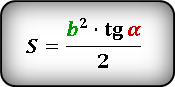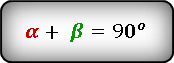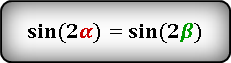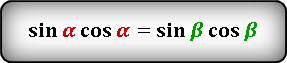Содержание:
- Формула
- Примеры вычисления площади прямоугольного треугольника
Формула
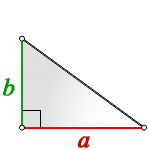
Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1),
надо найти произведение катетов
$a$ и
$b$ и поделить его на два. То есть
$$mathrm{S}_{Delta A B C}=frac{a b}{2}$$
Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.
Примеры вычисления площади прямоугольного треугольника
Пример
Задание. Найти площадь прямоугольного треугольника
$ABC$, если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
$mathrm{S}_{Delta A B C}=frac{3 cdot 4}{2}=frac{12}{2}=6$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.
Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора,
найдем второй катет заданного треугольника:
$b=sqrt{10^{2}-6^{2}}=sqrt{100-36}=sqrt{64}=8$ (см)
Тогда площадь
$S=frac{6 cdot 8}{2}=frac{48}{2}=24$ (см2)
Ответ. $S=24$ (см2)
Читать дальше: как найти площадь равнобедренного треугольника.
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
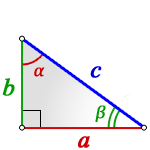
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
a, b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a, b — катеты
α, β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
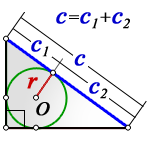
3. Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c1, c2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
- Подробности
-
Опубликовано: 07 сентября 2011
-
Обновлено: 13 августа 2021
Площадь прямоугольного треугольника
Ирина Алексеевна Антоненко
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как вычислить площадь прямоугольного треугольника, также здесь вы найдёте онлайн-калькуляторы для вычисления площади прямоугольного треугольника по различным заданным величинам.
Определение 1
Прямоугольный треугольник — это треугольник, один из углов которого является прямым, при этом два другие угла — острые.
Для того чтобы воспользоваться приведёнными онлайн-калькуляторами для расчётов, введите известные величины.
Одной из самых простых формул для вычисления площади прямоугольного треугольника является формула через катеты.
Площадь прямоугольного треугольника по двум катетам
Формула площади прямоугольного треугольника по двум катетам выглядит как:
$S = frac12 cdot a cdot b$, где
$S$ — площадь треугольника,
$a$ — первый катет данного треугольника,
$b$ — второй катет данного треугольника.
Пример 1
Задача
Дан прямоугольный треугольник, две меньшие стороны которого равны $3$ и $4$. Чему равна его площадь?
Решение:
Самой длинной стороной в треугольнике является гипотенуза, поэтому воспользуемся формулой вычисления площади через катеты:
$S = frac12 cdot a cdot b = frac12 cdot 3 cdot 4 = 6$.
Ответ: $6$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Также площадь прямоугольного треугольника можно вычислить если известна гипотенуза и угол между гипотенузой и одним из катетов.
Площадь прямоугольного треугольника по гипотенузе и углу
Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними:
$S = frac12 cdot a cdot c cdot sin (α)$ (1).
Для начала необходимо найти одну из его сторон.
Для этого вспомним определение косинуса:
$cos (α) = frac{a}{c}$.
Из него выразим сторону $a$:
$a = c cdot cos (α)$.
Подставим $a$ в формулу (1):
$S = frac12 c^2 cdot cos (α) cdot sin (α)$, здесь
$c$ — гипотенуза;
$α$ — угол между сторонами $a$ и $c$.
Пример 2
Задача
Гипотенуза прямоугольного треугольника равна $7$, а угол $α$ между гипотенузой и катетом $a$ равен $30°$. Найдите, чему равна площадь треугольника.
Решение:
Найдём сторону $a$:
$a = c cdot cos (30°) ≈ 7 cdot 0.866 ≈ 6.06$
Подставим полученное значение для вычисления площади треугольника через синус угла:
$S = frac12 cdot a cdot c cdot sin (α) = frac12 cdot 6.06 cdot 7 cdot 0.5 = 10.605$.
Ответ: $10.605$.
Другим способом вычисления площади прямого треугольника является вычисление через формулу Герона.
Площадь прямоугольного треугольника по формуле Герона
Рассчитать площадь прямоугольного треугольника по формуле Герона можно следующим образом:
$S = (p — a) cdot (p — b)$, где
$S$ — площадь треугольника,
$a$ — первый катет,
$b$ — второй катет,
$p$ — полупериметр данного треугольника, вычисляемый по формуле:
$p = frac{a + b + c}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 10.06.2019
|
Хотелось бы собрать разные формулы в зависимости от того, какие элементы треугольника заданы. площадь прямоугольного треугольника можно вычислить:
s=a x b/2,где a,b — длины катетов.. площадь прямоугольного треугольника — половина площади прямоугольника со сторонами, равными катетам данного треугольника..
tg c =a/b, где а — противолежащий углу с катет, b — прилежащий к углу с катет, tgc — тангенс угла с.. откуда b=a/tg c и тогда: s=a2/tg c-если задан катет и прилежащий к нему угол: s=b2 x tg c.. -если задана высота и один из катетов: d / a=sin c, d/b=sin(90-c), откуда складывая оба треугольника ( катеты — высота, а гипотенузы — катеты большого треугольника ): s=d2(1/sin c + 1/sin ( 90-c )=d2 ( 1/ sin c + 1/cos c ),где d — высота треугольника, с — угол.. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Наиболее распространенная формула для вычисления площади прямоугольного треугольника выводится очень просто. Если взять прямоугольник и провести в нём диагональ, то получим 2 равных прямоугольных треугольника. Площадь прямоугольника равна произведению сторон: S = a *b. Так как прямоугольный треугольник — это 1/2 часть от прямоугольника, то его площадь будет равна половине произведения катетов: Если даны оба катета, то тут всё понятно — подставляем эти значения формулу и всё. Если дана гипотенуза и один из катетов, то нужно с помощью теоремы Пифагора найти другой катет. Например, гипотенуза c = 10 см. и катет a = 6 см. Чтобы найти катет b, нужно воспользоваться формулой b = √(c² — a²) = √(100 — 36) = √64 = 8 см. Следовательно, S = 0,5 * 6 * 8 = 24 см. Также есть формулы, позволяющие найти площадь прямоугольного треугольника через известные углы. Если известна сторона и один из острых углов, то в первую очередь определяем неизвестный угол. Пусть дан катет a и противолежащий угол α = 30°. Тогда угол β = 180° — 90° — 30° = 60°. Площадь прямоугольного треугольника в этом случае будет определяться по формуле: Осталось лишь подставить известные значения в эту формулу и посчитать площадь. МарияСС 6 лет назад Нам подойдут формулы, по которым мы можем найти площадь любого треугольника. 1) 1/2*h*a. Половина произведения высоты на основание. В случае прямоугольного треугольника формула та же, только высота у нас будет одним из катетов. 2) по формуле Герона. S=p*(p−a)*(p−b)*(p−c). a, b и с — это стороны треугольника. p — полупериметр p=1/2*(a+b+c) 3) S=1/2*a*b*sin(γ). По двум сторонам и углу между ними. Зная тригонометрию, можно переделывать данную формулу под различные варианты данных углов. Заучивать все модификации не имеет смысла. Здесь необходимо понять смысл и в конечном итоге все равно приходить к изначальной формуле. 88SkyWalker88 7 лет назад Треугольник — это такая фигура, которая образуется путем соединения трех точек, которые не лежат на одной прямой. Эти три точки будут называться вершинами треугольника. А отрезки, которые соединяют эти самые точки, это его стороны. Если у треугольника один из углов будет являться прямым, то такой треугольник будут называть прямоугольным. Возьмем к примеру этот треугольник: Чтобы найти площадь треугольника, нужно воспользоваться таким правилом: его площадь равна половине произведения катетов. Формулой это будет выражаться следующим образом: S = 1/2 * ab, где a и b являются катетами данного треугольника. Площадь прямоугольного треугольника легко находится из того соображения, что два одинаковых прямоугольных треугольника, если их сложить гипотенузами, дают прямоугольник со сторонами, равными катетам. Площадь этого прямоугольника — произведение катетов, поэтому площадь треугольника — половина произведения катетов. Oleg74 10 лет назад Треугольник — это геометрическая фигура, образованая из трех отрезков, соединенных между собой тремя точками, называемыми вершинами. В прямоугольном треугольнике один угол равен 90 градусов. Общая формула для определения площади прямоугольного треугольника : S = 1/2 * ab, где a,b — катеты треугольника ABC. Limitless 7 лет назад Начнём с того, что у прямоугольного треугольника один из углов равен девяноста градусам. Таким образом, две стороны треугольника, которые прилегают к прямому углу носят название катетов. Площадь подобного треугольника будет вычисляться, как делённое пополам произведение катетов. moreljuba 7 лет назад Прямоугольным называется тот треугольник, который имеет прямой угол. Итак, для того чтобы рассчитать площадь прямоугольного треугольника необходимо воспользоваться следующей формулой: Площадь=1/2*первый катет*второй катет. Нужно длину одного катета умножить на длину второго и разделить полученное число на два. Нас в школе, для примера учили условно дорисовывать второй прямоугольный треугольник в перевернутом виде что бы вместе с первым получился прямоугольник а его площадь как известно равно длина умноженная на ширину, и треугольник это половина прямоугольника. аллаgruz 9 лет назад Здесь всё зависит от того, какиеараметры прямоугольного треугольника даны. В конечном же итоге, решение выводится из теоремы Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Небольшие преобразования и ответ готов. Знаете ответ? |