Как найти площадь треугольника вписанного в параллелограмм

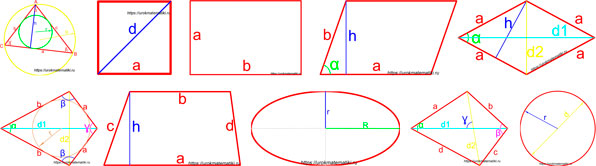
Формулы площадей фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p — a p — b p — c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,

где a, b — стороны треугольника,
γ — угол между сторонами a и b .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Формулы площади квадрата

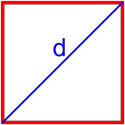
Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

где S — площадь квадрата,
a — длина стороны квадрата.

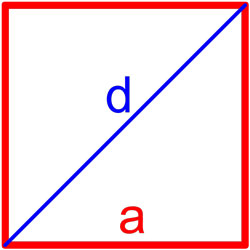
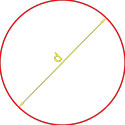
Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

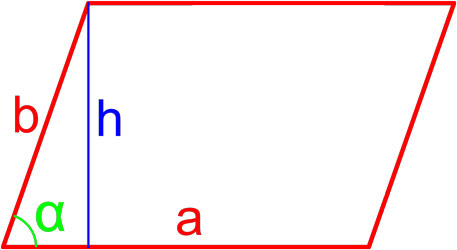
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.

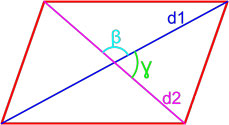
Формула площади параллелограмма по двум диагоналям и углу между ними

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.

Формулы площади ромба

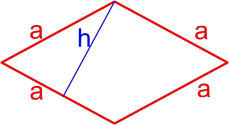
Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

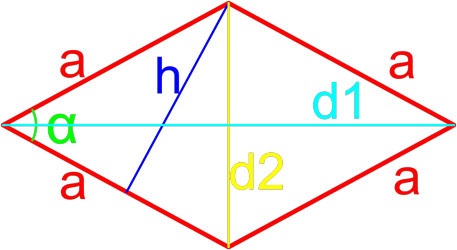
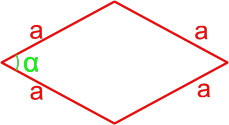
Формула площади ромба по длине стороны и углу

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

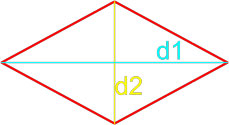
Формула площади ромба по длинам его диагоналей

Площадь ромба равна половине произведению длин его диагоналей.

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

Формулы площади трапеции

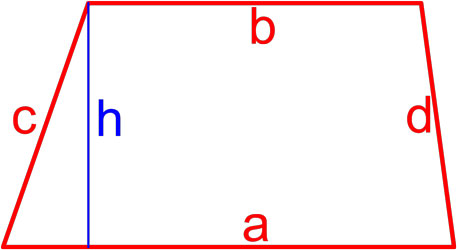
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).

Формула Герона для трапеции

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.

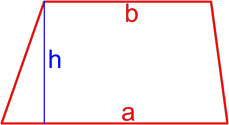
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы её оснований на высоту.

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Формулы площади дельтоида

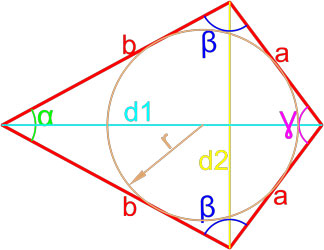
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

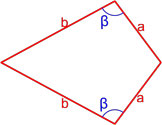
Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.

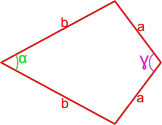
Формула площади дельтоида по равным сторонам и углу между ними

Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a 2 sin γ + b 2 sin α 2 ,

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .

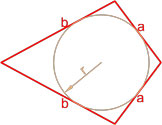
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

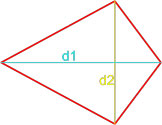
Формула площади дельтоида по двум диагоналям

Площадь дельтоида равна половине произведения длин двух диагоналей.

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Формулы площади произвольного выпуклого четырехугольника

Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

S = d1 · d2 · sin γ 2 ,

где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

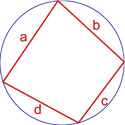
Формула площади вписанного четырехугольника (формула Брахмагупты)

Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p — a p — b p — c p — d ,

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.

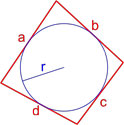
Формула площади четырехугольника с вписанной окружностью

Если в четырехугольник можно вписать окружность, то его площадь равна:

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.

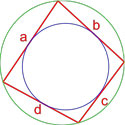
Формула площади четырехугольника с вписанной и описанной окружностями

Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Формулы площади круга

Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

S = π r 2 ,

где S — площадь круга,
r — радиус круга.

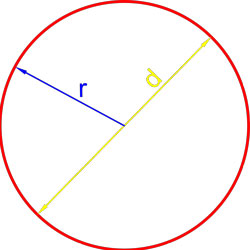
Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — площадь круга,
d — диаметр круга.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

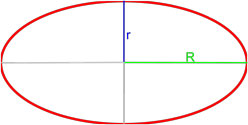
Формула площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

Площадь параллелограмма

Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.

Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Площадь параллелограмма по основанию и высоте параллелограмма

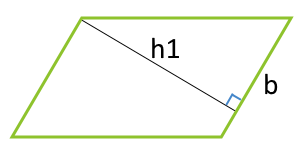
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

Площадь параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма по двум диагоналям и углу между этими диагоналями

Площадь параллелограмма по вписанной окружности и стороне

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Площадь параллелограмма по вписанной окружности и углу между сторонами

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади параллелограмма

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	основание и высота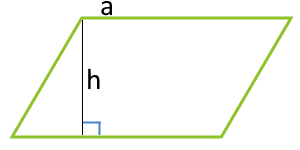
2	сторона и высота, опущенная на эту сторону
3	две стороны и угол между ними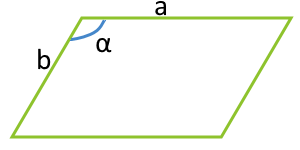
4	диагонали и угол между ними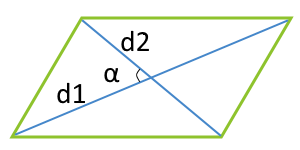
5	вписанная окружность и сторона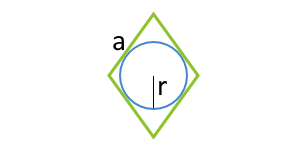
6	вписанная окружность и угол между сторонами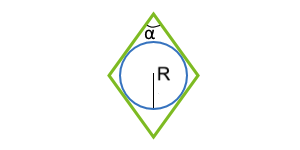

Определения

Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.

Некоторые свойства параллелограмма:

• Сумма углов параллелограмма равна 360 градусов
• Сумма углов, прилегающих к любой из сторон равна 180 градусов
• Противоположные стороны параллельны и имеют одинаковую длину
• Противолежащие углы равны

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Как найти площадь параллелограмма, треугольника, трапеции

Вы будете перенаправлены на Автор24

Площадь параллелограмма

Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

где $a$ сторона параллелограмма, $h$ — высота, проведенная к этой стороне.

Доказательство.

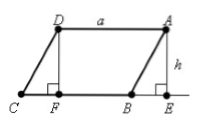
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).

Очевидно, что фигура $FDAE$ — прямоугольник.

[angle BAE=<90>^0-angle A, ] [angle CDF=angle D-<90>^0=<180>^0-angle A-<90>^0=<90>^0-angle A=angle BAE]

Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда

Значит по теореме о площади прямоугольника:

Теорема доказана.

Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.

Доказательство.

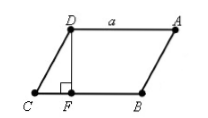
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).

По определению синуса, получим

Значит, по теореме $1$:

Теорема доказана.

Площадь треугольника

Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

где $a$ сторона треугольника, $h$ — высота, проведенная к этой стороне.

Доказательство.

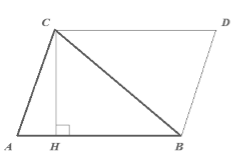
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

Значит по теореме $1$:

Теорема доказана.

Готовые работы на аналогичную тему

Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

где $a, b$ стороны треугольника, $alpha $ — угол между ними.

Доказательство.

Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

Значит по теореме $1$:

Теорема доказана.

Площадь трапеции

Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.

Математически это можно записать следующим образом

Доказательство.

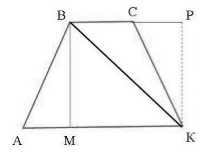
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).

По теореме $3$, получим

Теорема доказана.

Пример задачи

Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$

Решение.

Так как треугольник равносторонний, то все его углы равняются $<60>^0$.

Тогда, по теореме $4$, имеем

Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 05 2021

2023-02-16   

Доказать, что площадь треугольника, вписанного в параллелограмм, не может быть больше половины площади этого параллелограмма.

Решение:

Первый случай. Предположим, что две вершины треугольника $A$ и $B$ лежат на одной и той же стороне $KL$ параллелограмма (рис.).

Если $S$ — площадь треугольника $ABC$, $m$ — его высота, опущенная на сторону $AB, S^{ prime}$ — площадь параллелограмма и $n$ — высота параллелограмма, опущенная на сторону $KL$, то

$S = frac{1}{2} m cdot AB, S^{ prime} = n cdot KL$

а поскольку

$m leq n$ и $AB leq KL$,

то

$S leq frac{1}{2} S^{ prime}$

Второй случай. Предположим, что вершины треугольника принадлежат различным сторонам параллелограмма (рис.). Тогда среди вершин треугольника заведомо найдутся две такие, которые находятся на противоположных сторонах параллелограмма. Пусть вершина $A$ лежит на стороне $KL$, вершина $B$ — на противоположной стороне $MN$ и вершина $C$ — на стороне $KN$.

Проведем через вершину $C$ прямую, параллельную сторонам $KL$ и $MN$. Пусть $D$ — точка пересечения этой прямой со стороной треугольника $AB$, а $E$ — точка ее пересечения со стороной параллелограмма $LM$.

По доказанному выше (при рассмотрении первого случая) площадь треугольника $ACD$ не больше половины площади параллелограмма $KLEC$, а площадь треугольника $CDB$ не превосходит половины площади параллелограмма $CEMN$. Но отсюда следует, что площадь всего треугольника $ABC$ не превосходит половины площади параллелограмма $KLMN$.

Заметим, что площади всех четырех треугольников не изменятся, если мы «выпрямим» параллелограмм — то есть перейдем к рассмотрению прямоугольника, сохранив при этом основание, высоту и пропорции, в которых вершины треугольников делят стороны (рис. 2). Это так, потому что, как мы помним из школы, площадь треугольника равна половине произведения основания на высоту (ни то, ни другое здесь не меняется, как видно из рисунка), а площадь параллелограмма равна просто произведению основания на высоту (и при переходе к прямоугольнику не меняется). Итак, вместо параллелограмма можно рассматривать прямоугольник.

Прежде чем решать задачу с большими числами и в общем случае, давайте проведем небольшое исследование для маленьких площадей. На рис. 3 показан прямоугольник 5×4, разбитый на четыре треугольника. Нетрудно увидеть, что площадь красного треугольника равна 3, площадь желтого равна 4, а площадь зеленого равна 5. Как и в условии задачи, площади трех треугольников являются последовательными натуральными числами (причем в том же порядке). Площадь оранжевого треугольника при этом равна 5×4 – (3+4+5) = 8.

На рис. 4 показан прямоугольник 13×10 с аналогичным разбиением на треугольники. Их площади (в том же порядке) равны 24, 25 и 26. Площадь внутреннего треугольника равна 55. Как связаны между собой числа в этих четверках?

Введем обозначения как показано на рис. 5 и пусть 2S — площадь всего прямоугольника. Обратите внимание, что (a) и (b) — это не длины, а дробные доли от сторон прямоугольника.

Тогда (S_1/S=ab), (S_2/S=1-a), (S_3/S=1-b). Из второго и третьего равенств следует: (Scdot a=S-S_2) и (Scdot b=S-S_3). Значит, (Sacdot Sb=(S-S_2)(S-S_3)=S^2-(S_2+S_3)S+S_2S_3). Учитывая, что (ab=S_1/S), получим равенство (S_1cdot S=S^2-(S_2+S_3)S+S_2S_3), которое можно переписать в виде квадратного уравнения:

[S^2-(S_1+S_2+S_3)S+S_2S_3=0.]

Воспользуемся тем, что числа (S_1), (S_2) и (S_3) в таком порядке являются последовательными натуральными числами: (S_3=S_2+1) и (S_1+S_2+S_3=3S_2). Получим:

[S^2-3S_2cdot S+S_2(S_2+1)=0.]

Решим это уравнение относительно (S):

[S=frac{3S_2pm sqrt{5S_2^2-4S_2}}{2}.]

Отсюда (X=2S-3S_2=pmsqrt{5S_2^2-4S_2}), и, поскольку площадь положительна, окончательно получаем

[X=sqrt{5S_2^2-4S_2}.]

Итак, (sqrt{5S_2^2-4S_2}=2584). Положительный корень этого уравнения (S_2=1156). Вычитая единицу, находим (S_1=1155). Соответствующий прямоугольник имеет размеры 89×68.