Как найти площадь треугольника вписанного в прямоугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

Треугольник вписан в прямоугольник

Если треугольник произвольно вписывать в прямоугольник, то задача окажется слишком многовариантной. Поэтому я решил принять важное ограничение: допустим вершина треугольника А является также и вершиной описанного прямоугольника. В этом случае прямоугольников хоть и бесконечно много, но среди них есть как самый большой по площади, так и самый малый. Какие же они, эти площади, если известны стороны треугольника «a», «b», «c» ?

Довольно несложное дифференциальное исчисление позволило определить нужные углы поворота «t». Это дало возможность при помощи теоремы косинусов найти и экстремальные площади прямоугольников. Формулы, показанные на рисунке, в который раз меня очаровали!

Как и очаровал снег после очень тёплой недели. Когда температура достигала +18 градусов. Утром смотрю в окошко — все деревья в красочном инее!

Прямоугольный треугольник

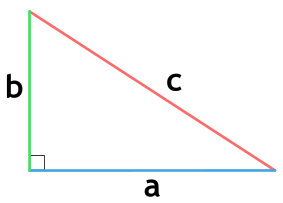
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

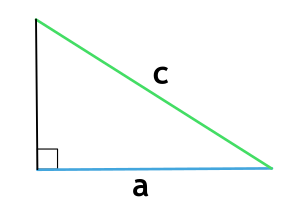
Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

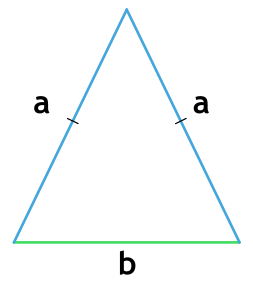
Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
Поделите все на 4.

Если известна сторона и высота

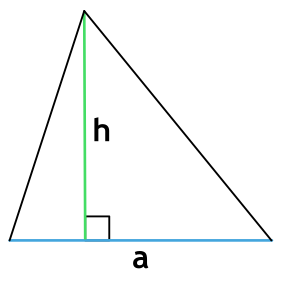
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

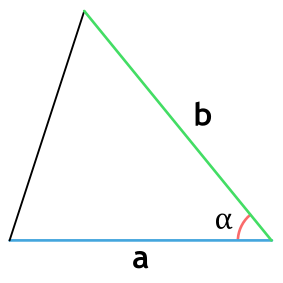
Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

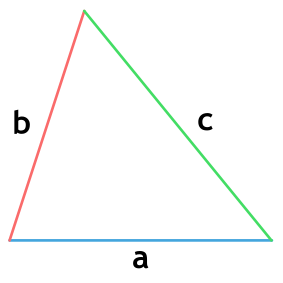
Если известны длины трех сторон

Найдите периметр. Для этого сложите все три стороны.
Найдите полупериметр – разделите периметр на два. Запомните значение.
Отнимите от полупериметра длину первой стороны. Запомните.
Отнимите от полупериметра длину второй стороны. Тоже запомните.
Отнимите от полупериметра длину третьей стороны. И ее запомните.
Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

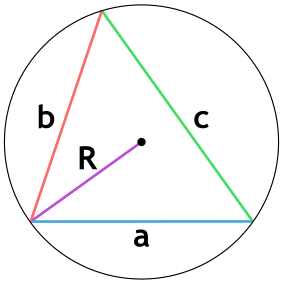
Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

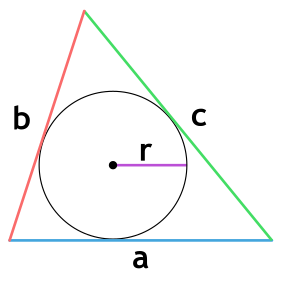
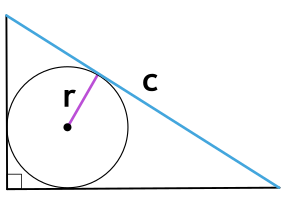
Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

источники:

Прямоугольный треугольник

http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika

Источник

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

33 472

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Если он равнобедренный

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
Поделите все на 4.

Если известна сторона и высота

Если известны две стороны и градус угла между ними

Если известны длины трех сторон

Делайте так:

Найдите периметр. Для этого сложите все три стороны.
Найдите полупериметр – разделите периметр на два. Запомните значение.
Отнимите от полупериметра длину первой стороны. Запомните.
Отнимите от полупериметра длину второй стороны. Тоже запомните.
Отнимите от полупериметра длину третьей стороны. И ее запомните.
Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Если известны три стороны и радиус вписанной окружности

( 32 оценки, среднее 4.44 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given here is an ellipse with axes length 2a and 2b, which inscribes a rectangle of length l and breadth h, which in turn inscribes a triangle.The task is to find the area of this triangle.
Examples:

Input: a = 4, b = 3
Output: 12

Input: a = 5, b = 2
Output: 10

Approach:
We know the Area of the rectangle inscribed within the ellipse is, Ar = 2ab(Please refer here),
also the area of the triangle inscribed within the rectangle s, A = Ar/2 = ab(Please refer here)
Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>

using namespace std;

float area(float a, float b)

{

if (a < 0 || b < 0)

return -1;

float A = a * b;

return A;

}

int main()

{

float a = 5, b = 2;

cout << area(a, b) << endl;

return 0;

}

Java

import java.io.*;

class GFG {

static float area(float a, float b)

{

if (a < 0 || b < 0)

return -1;

float A = a * b;

return A;

}

public static void main (String[] args) {

float a = 5, b = 2;

System.out.println(area(a, b));

}

Python3

def area(a, b):

if (a < 0 or b < 0):

return -1

A = a * b

return A

if __name__ == '__main__':

a = 5

b = 2

print(area(a, b))

C#

using System;

class GFG

{

static float area(float a, float b)

{

if (a < 0 || b < 0)

return -1;

float A = a * b;

return A;

}

static public void Main ()

{

float a = 5, b = 2;

Console.WriteLine(area(a, b));

}

PHP

<?php

function area($a, $b)

{

if ($a < 0 || $b < 0)

return -1;

$A = $a * $b;

return $A;

}

$a = 5;

$b = 2;

echo area($a, $b);

?>

Javascript

<script>

function area(a , b)

{

if (a < 0 || b < 0)

return -1;

var A = a * b;

return A;

}

var a = 5, b = 2;

document.write(area(a, b));

</script>

Time complexity: O(1)

Auxiliary Space: O(1)

Last Updated :
28 Jun, 2022

Like Article

Save Article

Источник

Как найти площадь любого треугольника

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

Умножьте сторону треугольника на высоту, проведённую к этой стороне.
Поделите результат на два.

S — искомая площадь треугольника.
a — сторона треугольника.
h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

Посчитайте произведение двух известных сторон треугольника.
Найдите синус угла между выбранными сторонами.
Перемножьте полученные числа.
Поделите результат на два.

S — искомая площадь треугольника.
a и b — стороны треугольника.
α — угол между сторонами a и b.

Зная три стороны (формула Герона)

Посчитайте разности полупериметра треугольника и каждой из его сторон.
Найдите произведение полученных чисел.
Умножьте результат на полупериметр.
Найдите корень из полученного числа.

S — искомая площадь треугольника.
a, b, c — стороны треугольника.
p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

Найдите произведение всех сторон треугольника.
Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

S — искомая площадь треугольника.
R — радиус описанной окружности.
a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

S — искомая площадь треугольника.
r — радиус вписанной окружности.
p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

Посчитайте произведение катетов треугольника.
Поделите результат на два.

S — искомая площадь треугольника.
a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

Умножьте основание на высоту треугольника.
Поделите результат на два.

S — искомая площадь треугольника.
a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

Умножьте квадрат стороны треугольника на корень из трёх.
Поделите результат на четыре.

S — искомая площадь треугольника.
a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

7 причин полюбить математику
ТЕСТ: Помните ли вы геометрию?
10 хитрых головоломок со спичками для тренировки воображения
Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
ТЕСТ: Сможете ли вы решить простые математические примеры?

Источник

{S = dfrac{1}{2} cdot a cdot h}

Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.

Калькулятор площади треугольника
Площадь треугольника
1. через основание и высоту
2. через две стороны и угол между ними
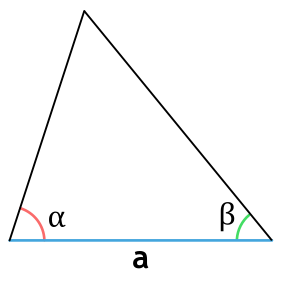
3. через сторону и два прилежащих угла
4. через радиус описанной окружности и 3 стороны
5. через радиус вписанной окружности и 3 стороны
6. по формуле Герона
Площадь прямоугольного треугольника
1. через катеты
2. через гипотенузу и прилежащий угол
3. через катет и прилежащий угол
4. через радиус вписанной окружности и гипотенузу
5. через вписанную окружность
6. по формуле Герона
7. через катет и гипотенузу
Площадь равнобедренного треугольника
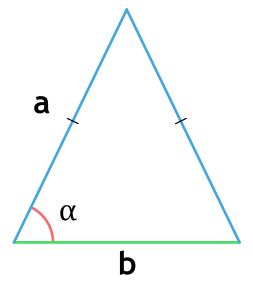
1. через основание и сторону
2. через основание, боковую сторону и угол
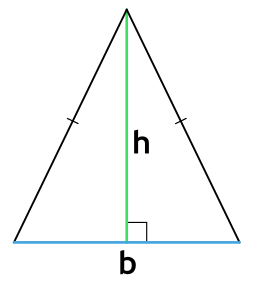
3. через основание и высоту
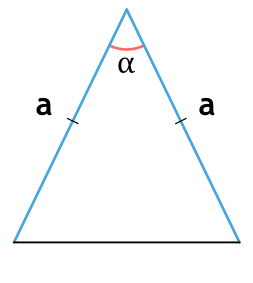
4. через боковые стороны и угол между ними
5. через основание и угол между боковыми сторонами
Площадь равностороннего треугольника
1. через сторону
2. через высоту
3. через радиус описанной окружности
4. через радиус вписанной окружности
Примеры задач

Площадь треугольника

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Площадь треугольника через основание и высоту

{S = dfrac{1}{2} cdot a cdot h}

a — длина основания

h — высота, проведенная к основанию

Площадь треугольника через две стороны и угол между ними

{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}

a и b — стороны треугольника

α — угол между сторонами a и b

Площадь треугольника через сторону и два прилежащих угла

{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 — (alpha + beta)}

a — сторона треугольника

α и β — прилежащие к стороне a углы

Площадь треугольника через радиус описанной окружности и 3 стороны

{S = dfrac{a cdot b cdot c}{4 cdot R}}

a, b и c — стороны треугольника

R — радиус описанной окружности

Площадь треугольника через радиус вписанной окружности и 3 стороны

{S = r cdot dfrac{a + b + c}{2}}

a, b и c — стороны треугольника

r — радиус вписанной окружности

Площадь треугольника по формуле Герона

{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}

a, b и c — стороны треугольника

p — полупериметр треугольника

Площадь прямоугольного треугольника

Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).

Площадь прямоугольного треугольника через катеты

{S = dfrac{1}{2} cdot a cdot b}

a и b — стороны треугольника

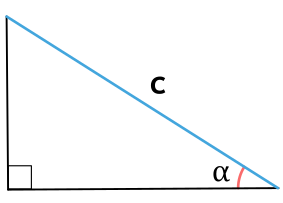
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол

{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}

c — гипотенуза прямоугольного треугольника

α — прилежащий к гипотенузе c угол

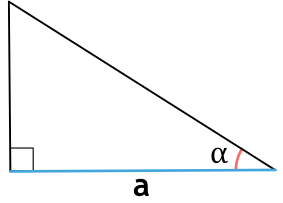
Площадь прямоугольного треугольника через катет и прилежащий угол

{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}

a — катет прямоугольного треугольника

α — прилежащий к катету a угол

Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

{S = r cdot (r+c)}

r — радиус вписанной окружности

c — гипотенуза прямоугольного треугольника

Площадь прямоугольного треугольника через вписанную окружность

{S = c_1 cdot c_2}

с₁ и с₂ — отрезки, полученные делением гипотенузы точкой касания окружности

Площадь прямоугольного треугольника по формуле Герона

{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}

a, b и c — стороны треугольника

p — полупериметр треугольника

Площадь прямоугольного треугольника через катет и гипотенузу

{S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2}}

a — катет прямоугольного треугольника

c — гипотенуза прямоугольного треугольника

Площадь равнобедренного треугольника

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.

Площадь равнобедренного треугольника через основание и сторону

{S = dfrac{b}{4} sqrt{4a^2 — b^2}}

a — боковая сторона равнобедренного треугольника

b — основание равнобедренного треугольника

Площадь равнобедренного треугольника через основание, сторону и угол

{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}

a — боковая сторона равнобедренного треугольника

b — основание равнобедренного треугольника

α — угол между основанием и боковой стороной

Площадь равнобедренного треугольника через основание и высоту

{S = dfrac{1}{2} cdot b cdot h}

b — основание равнобедренного треугольника

h — высота, проведенная к основанию равнобедренного треугольника

Площадь равнобедренного треугольника через боковые стороны и угол между ними

{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}

a — боковые стороны равнобедренного треугольника

α — угол между боковыми сторонами

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}

b — основание равнобедренного треугольника

α — угол между боковыми сторонами

Площадь равностороннего треугольника

Равносторонний треугольник — треугольник, у которого все стороны равны.

Площадь равностороннего треугольника через сторону

{S = dfrac{sqrt{3} cdot a^2}{4}}

a — сторона равностороннего треугольника

Площадь равностороннего треугольника через высоту

{S = dfrac{h^2}{sqrt{3}}}

h — высота равностороннего треугольника

Площадь равностороннего треугольника через радиус описанной окружности

{S = dfrac{3 sqrt{3} cdot R^2}{4}}

R — радиус описанной окружности

Площадь равностороннего треугольника через радиус вписанной окружности

{S = 3 sqrt{3} cdot r^2}

r — радиус описанной окружности

Примеры задач на нахождение площади треугольника

Задача 1

Найдите площадь треугольника со сторонами 13 14 15.

Решение

Для решения задачи воспользуемся формулой Герона.

S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}

Для начала нам необходимо найти полупериметр p:

p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21

Теперь можем подставить его в формулу Герона и найти ответ:

S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2

Ответ: 84 см²

Убедимся в правильности решения с помощью калькулятора .

Задача 2

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.

Решение

Воспользуемся формулой.

S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 — 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 — 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2

Ответ: 1344 см²

Проверим ответ на калькуляторе .

Задача 3

Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.

Решение

Задача аналогична предыдущей, поэтому решение очень похоже.

S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 — 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 — 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2

Ответ: 60 см²

Проверка .

Задача 4

Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2

Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2

Проверка .

Задача 5

Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.

Решение

В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.

S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 — 4^2} = sqrt{4 cdot 49 — 16} = sqrt{196 — 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2

Ответ: 6sqrt{5} : см^2 approx 13.41641

Проверка .

Задача 6

Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.

Решение

Решим эту задачу по анологии с предыдущей.

S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 — 30^2} = dfrac{30}{4} sqrt{4 cdot 289 — 900} = dfrac{30}{4} sqrt{1156 — 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2

Ответ: 120 см²

Проверка .

Задача 7

Найдите площадь равностороннего треугольника со стороной 12 см.

Решение

Используем для решения задачи формулу.

S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2

Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2

Проверка .

Источник