Как найти площадь одного из четырех треугольников находящихся в квадрате со стороной 4 см.
Вы зашли на страницу вопроса Как найти площадь одного из четырех треугольников находящихся в квадрате со стороной 4 см?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 1 — 4 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` — углы треугольника`ABC`; `a`, `b` и `c` — противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` — высоты к этим сторонам; `r` — радиус вписанной окружности;`R` — радиус описанной окружности; `2p=(a+b+c)` — периметр треугольника; `S` — площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` — формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь — найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` — точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` — середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL«||«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«||«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«||«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` — точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` — площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` — середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` — точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,
Попробуйте решить необычную задачку для первоклашек
Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).
Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.
Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Занимательная геометрия для начальной школы. Задания
Занимательная геометрия для младших школьников 1-4 классов
Задания на нахождение фигур и их количества
Цели использования заданий учителем: совершенствовать умения учащихся видеть, распознавать плоскостные геометрические фигуры.
Задания для организации фронтальной работы в классе
Задание 1. Найди на рисунке слева пять треугольников, а на рисунке справа пять четырехугольников.
Задание 2. Какой фигурой на рисунках является общая часть треугольника и четырехугольника?
Ответ: В левой фигуре — треугольник, в правой — пятиугольник.
Задание 3. Сколько отрезков проведено в каждом треугольнике? В какой фигуре больше треугольников — в левой или правой?
Ответ: В левом — восемь, в правом — шесть.
Задание 4. Найди и покажи на рисунке пять прямых углов. Построй прямой угол на бумаге в клетку.
Задание 5. У четырехугольника отрезали один угол. Сколько углов будет иметь образовавшаяся после этого фигура?
Задание 6. Найди на рисунке пять прямых углов, четыре треугольника и один четырехугольник.
Задание 7. Из каких фигур составлена елочка? Сколько этих фигур?
Ответ: Из треугольников; 6 фигур.
Задание 8. Сколько треугольников на этом рисунке?
Задание 9. Сколько прямоугольников здесь нарисовано?
Задание 10. Сколько на рисунке треугольников? Сколько на рисунке четырехугольников? Сколько всего фигур?
Ответ: Треугольников — 4, четырехугольников — 1, всего фигур — 5.
Задание 11. Какие фигуры были использованы при изображении домика?
Ответ: Прямоугольник, треугольник, многоугольник, круг, квадрат.
Задание 12. Сколько треугольников изображено на этом рисунке?
Задание 13. Сколько треугольников изображено на рисунке?
Задание 14. Сколько четырехугольников на чертеже?
Задание 15. Начерти такой же домик, не отрывая карандаша от бумаги. Проводить линию карандашом можно только один раз. Сколько у тебя получилось треугольников?
Задания 16. Сколько фигур на чертеже? Четырёхугольников? Треугольников?
Ответ: Всего фигур — 9, четырехугольников — 5, треугольников — 4.
Задание 17. Сколько прямоугольников изображено на чертеже?
Задание 18. Сколько на чертеже треугольников? Сколько на чертеже четырехугольников?
Ответ: Треугольников — 6, четырехугольников — 5.
Задание 19. Сколько четырехугольников изображено на чертеже?
Задние 20. Сколько треугольников изображено на чертеже?
Задание 21. Сколько квадратов изображено на чертеже?
Задание 22. Рассмотри рисунок и найди на фигуре три треугольника.
Задание 23. Рассмотри рисунок и найди на фигуре пять треугольников.
Задание 24. Карандаш нарисовал козочку. Похожа она? Сколько прямоугольников на рисунке? А сколько квадратов?
Ответ: Прямоугольников — 6, квадратов — 4.
Задание 25. Найди все многоугольники на чертеже.
Задание 26. Сколько спряталось многоугольников?
Ответ: а) 3, б) 6, в) 6.
Задание 27. Сколько треугольников в этой фигуре?
Задание 28. Сколько четырехугольников изображено на чертеже?
Задание 29. Сколько различных по величине треугольников можно увидеть на чертеже? Сколько всего на чертеже различных по величине квадратов?
Ответ: Треугольников — 18, квадратов — 3.
Задание 30. Найдите на фигуре 12 треугольников.
Задание 31. Сколько всего треугольников и сколько четырехугольников ты можешь найти на чертеже?
Задание 32. Найдите на фигуре 16 треугольников.
Ответ: Треугольников — 6, четырехугольников — 8.
Задание 33. Найди на чертеже 8 треугольников. Сколько из этих треугольников тупоугольных и сколько остроугольных?
Ответ: 5 тупоугольных, 3 остроугольных.
Задание 34. Найди на чертеже 8 треугольников и 5 четырехугольников. Сколько из треугольников прямоугольных, сколько тупоугольных, сколько остроугольных?
Ответ: 4 прямоугольных, 2 остроугольных и 2 тупоугольных.
Задания на составление заданных фигур из определенного числа одинаковых палочек
Цель использования заданий учителем: совершенствовать практические умения учащихся в построении плоскостных геометрических фигур в рамках решения нестандартных заданий.
Задание 1. Составь 2 одинаковых (равных) треугольника из 5 одинаковых палочек.
Задание 2. Составь 2 одинаковых (равных) квадрата из 7 одинаковых палочек.
Задание 3. Составь 3 равных треугольника из 7 одинаковых палочек.
Задание 4. Составь 4 равных треугольника из 9 одинаковых палочек.
Задание 5. Составь 3 равных квадрата из 10 одинаковых палочек.
Задание 6. Составь квадрат и 2 равных треугольника из 5 одинаковых палочек.
Задание 7. Составь квадрат и 4 равных треугольника из 9 одинаковых палочек.
Задание 8. Составь из 10 одинаковых палочек 2 квадрата: большой и маленький.
Задание 9. Составь из 9 одинаковых палочек 2 одинаковых квадрата и 4 равных треугольника. (Решение: из 7 палочек составляют 2 квадрата, (см. задачу 2) и делят каждый из квадратов на 2 треугольника, используя еще 2 палочки.)
Задание 10. Составь из 9 одинаковых палочек 5 треугольников. (Решение: 4 маленьких треугольника, полученных в результате пристроения одного к другому, образуют 1 большой треугольник.)
Задание 11. Как можно из 7 счетных палочек выложить 1 пятиугольник и 1 треугольник?
Задание 12. Из 9 счетных палочек составь 5 треугольников. Сверь с образцом.
http://mozgan.ru/Geometry/AreaTriangle
http://ped-kopilka.ru/nachalnaja-shkola/didakticheskie-materialy/zanimatelnaja-geometrija-dlja-nachalnoi-shkoly-zadanija.html
Сегодня задачка на логику и геометрию, как в школе. Это не нужно в ИТ, но иногда нужно отвлекаться.
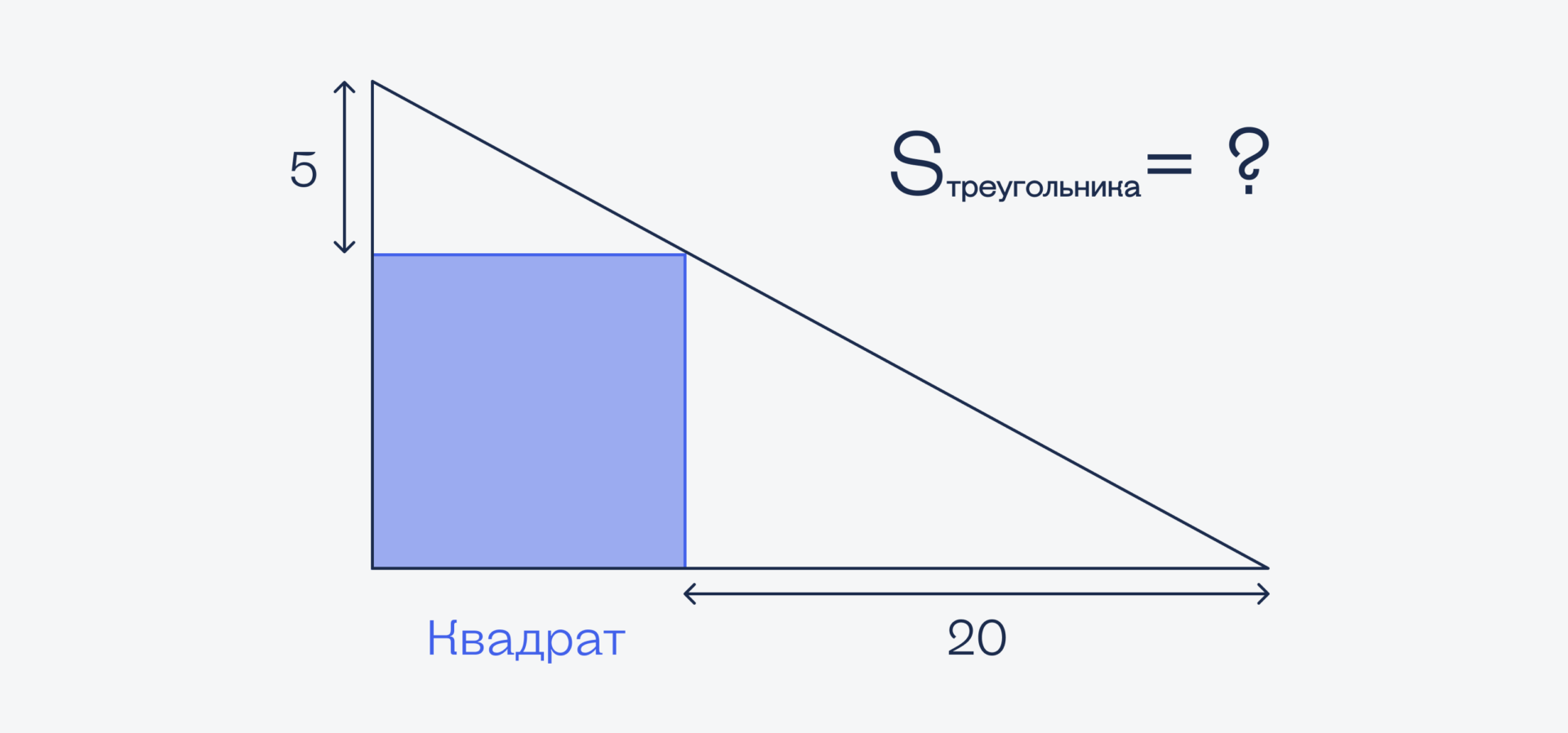
Вот картинка, тут всё понятно. Нужно найти площадь треугольника:
Решение с тригонометрией
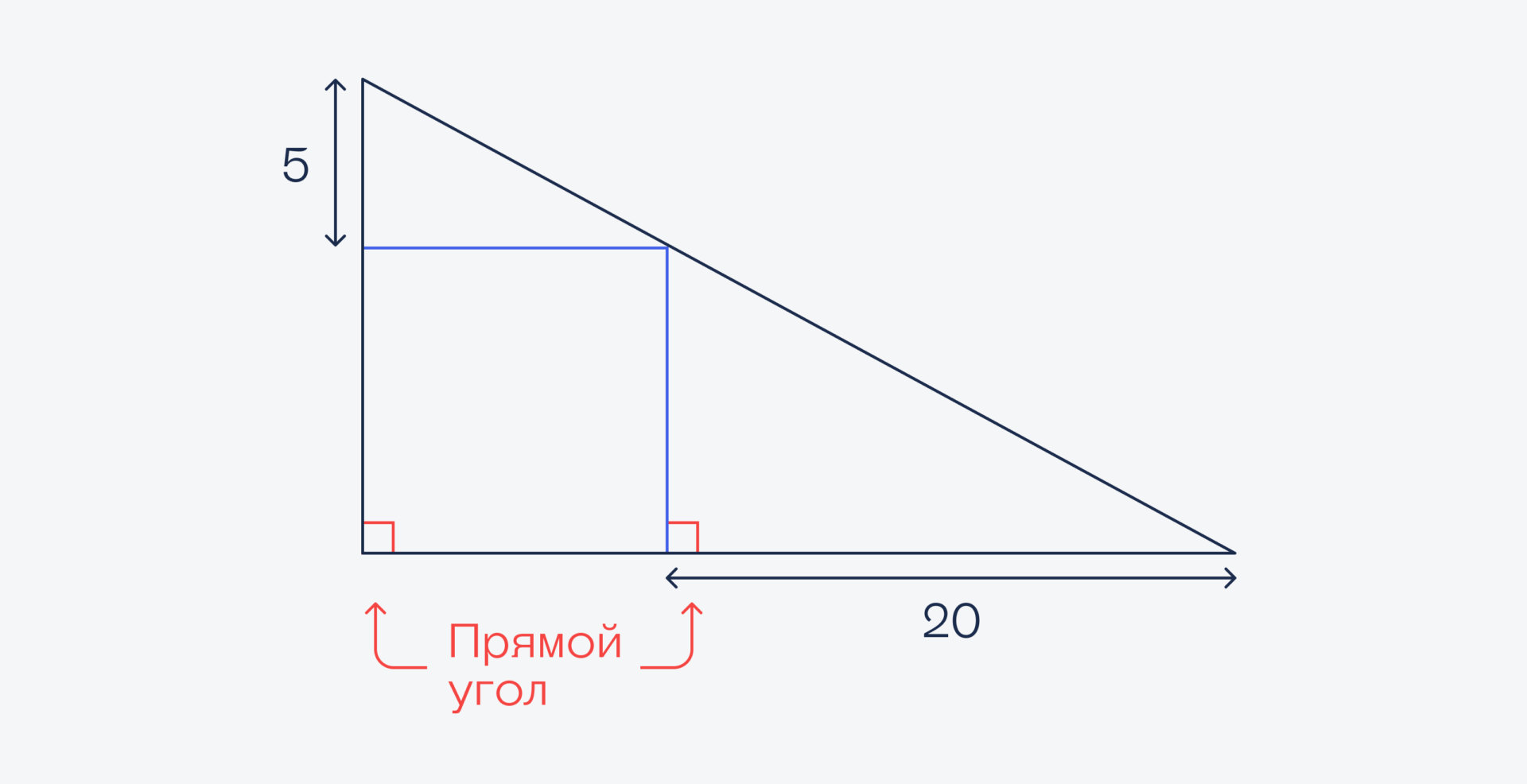
Так как у нас в треугольник вписан квадрат, это значит, что обе его стороны находятся под прямым углом к основанию треугольника:
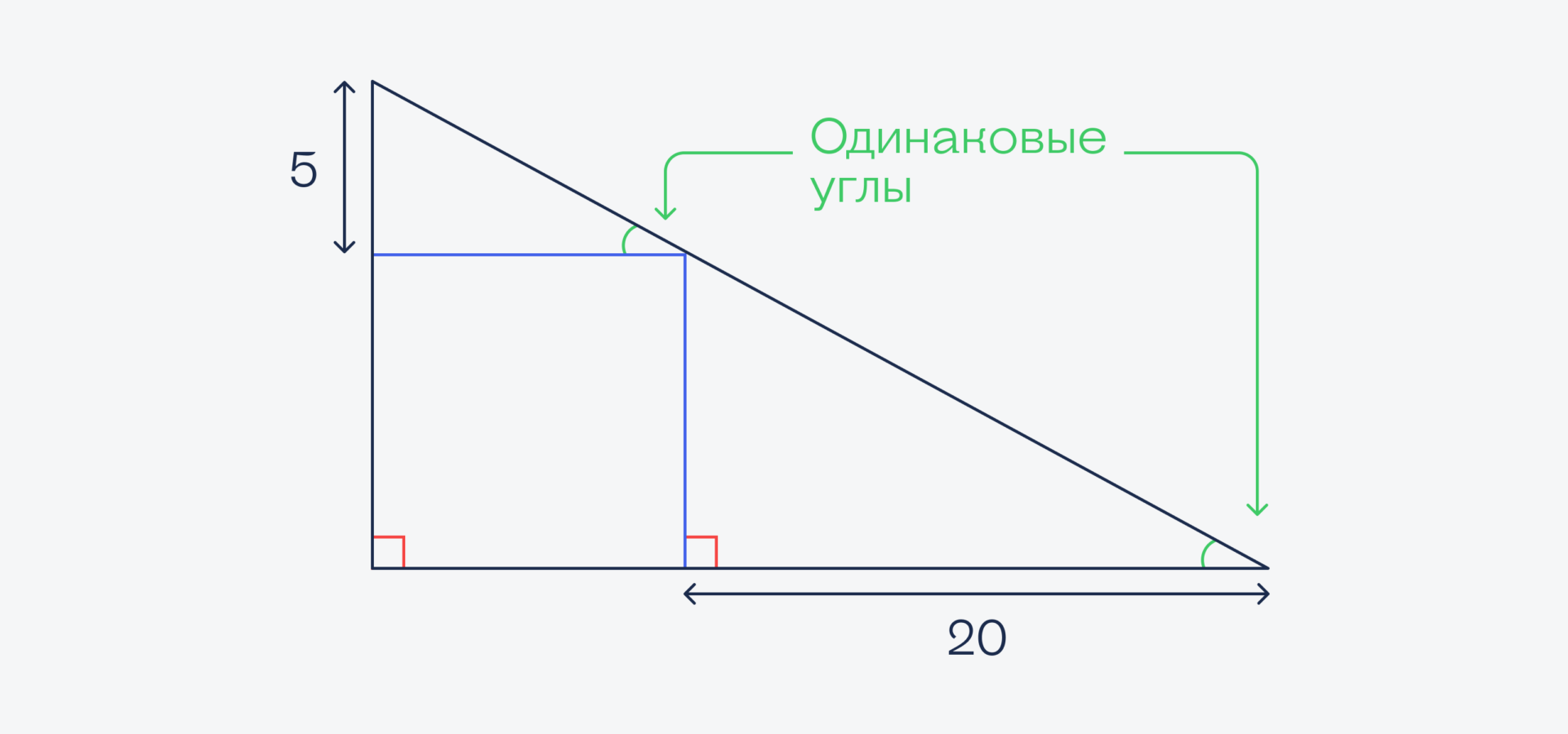
А раз так, то угол, который образуется при пересечении наклонной линии, совпадает с углом наклона этой линии к основанию:
Если у треугольников есть два одинаковых угла, то такие треугольники называются подобными. А раз они подобные, то и соотношение сторон у них будет одно и то же. Обозначим сторону квадрата за X:
Теперь построим соотношение:
5 / X = X / 20 ← решим это уравнение
X² = 5 × 20 = 100
X = 10
Зная сторону квадрата, можно легко найти площадь всего треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 225
Нестандартное решение без тригонометрии
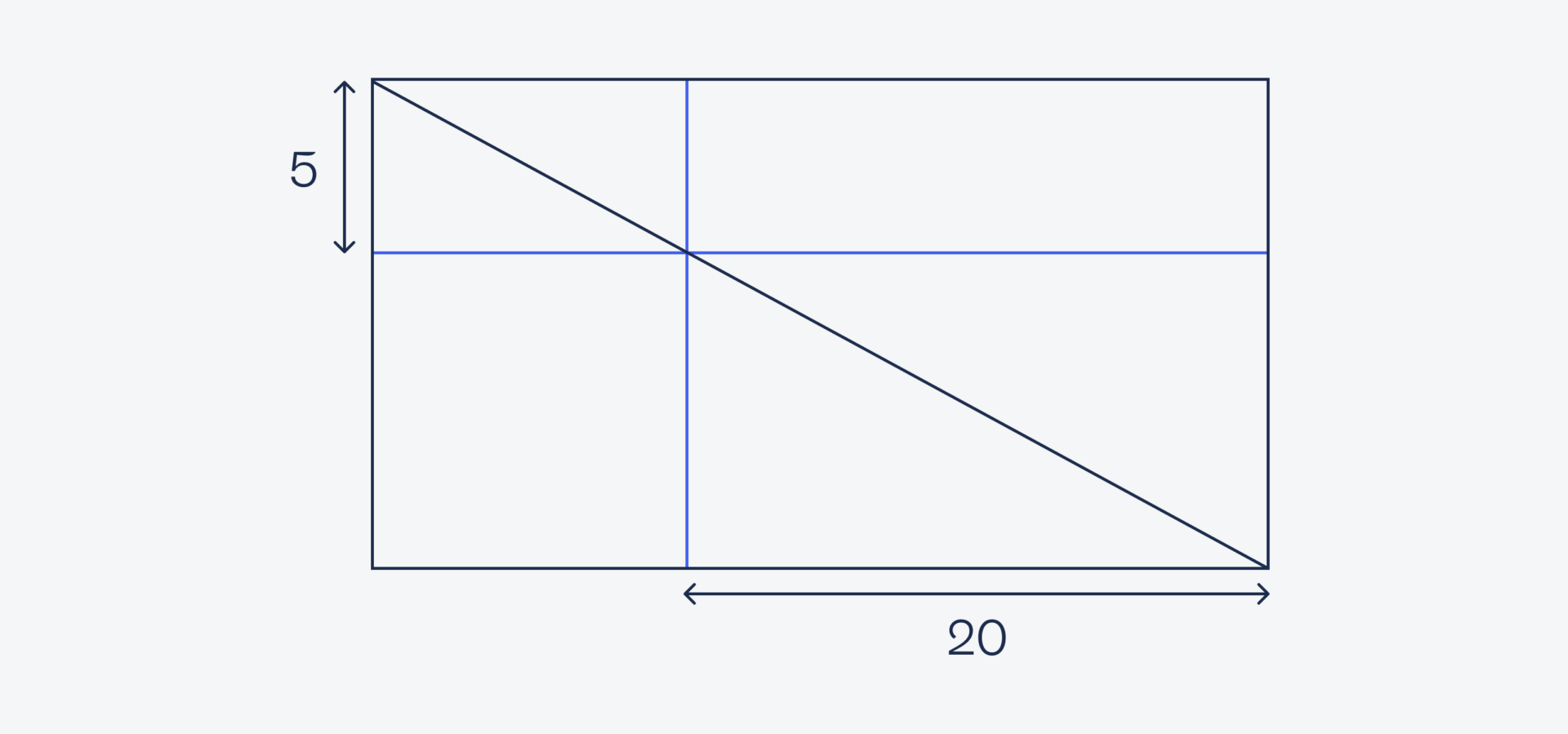
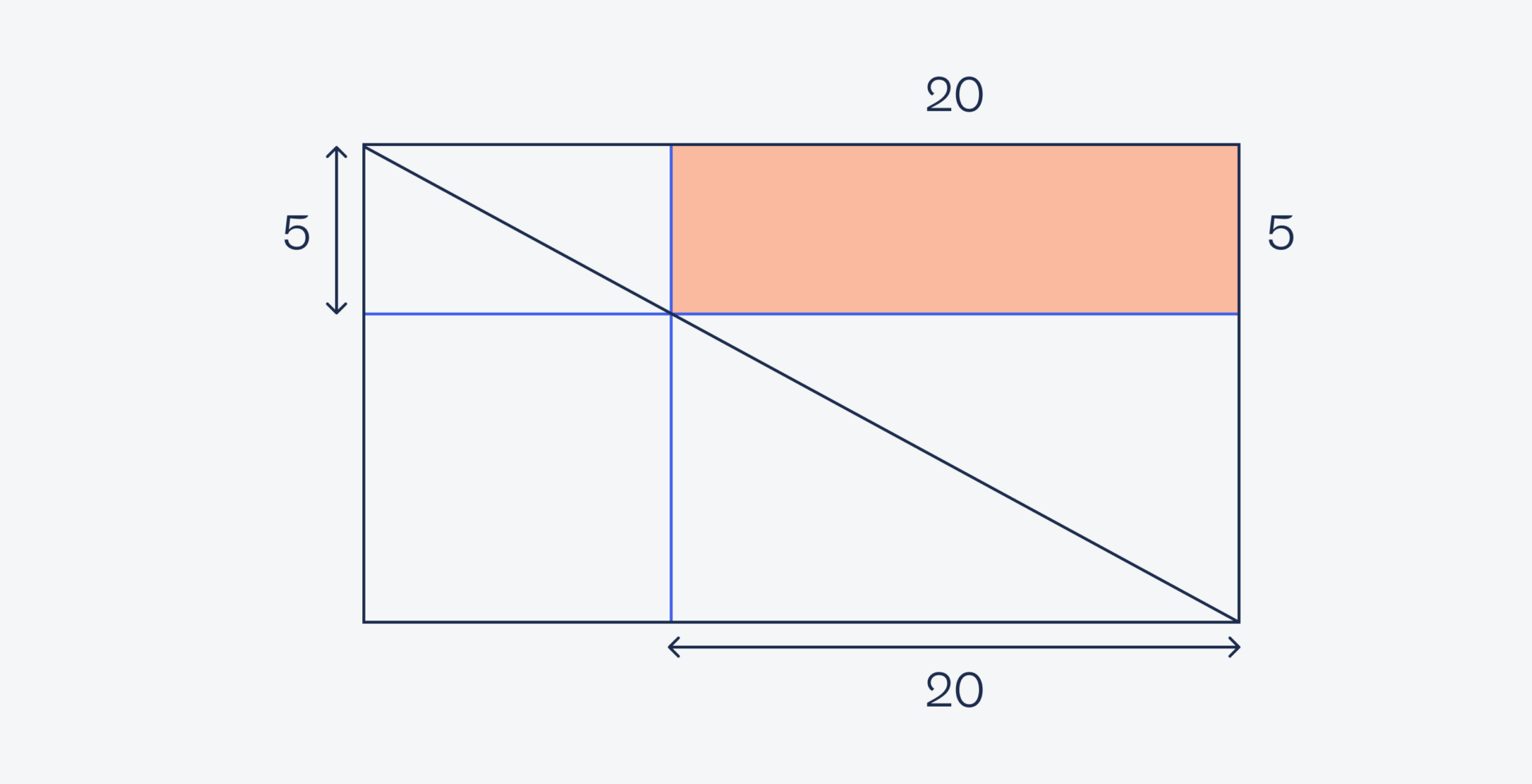
Представим, что мы ничего не знаем про тригонометрию, углы и подобие треугольников. Возьмём наш рисунок и мысленно достроим его до прямоугольника:
Так как у квадрата все углы прямые, то и синие линии у нас тоже пересекаются под прямыми углами между собой и с внешним прямоугольником. Это значит, что мы можем перенести известные размеры на оранжевый прямоугольник:
Зная длину и ширину, посчитаем его площадь — 5 × 20 = 100.
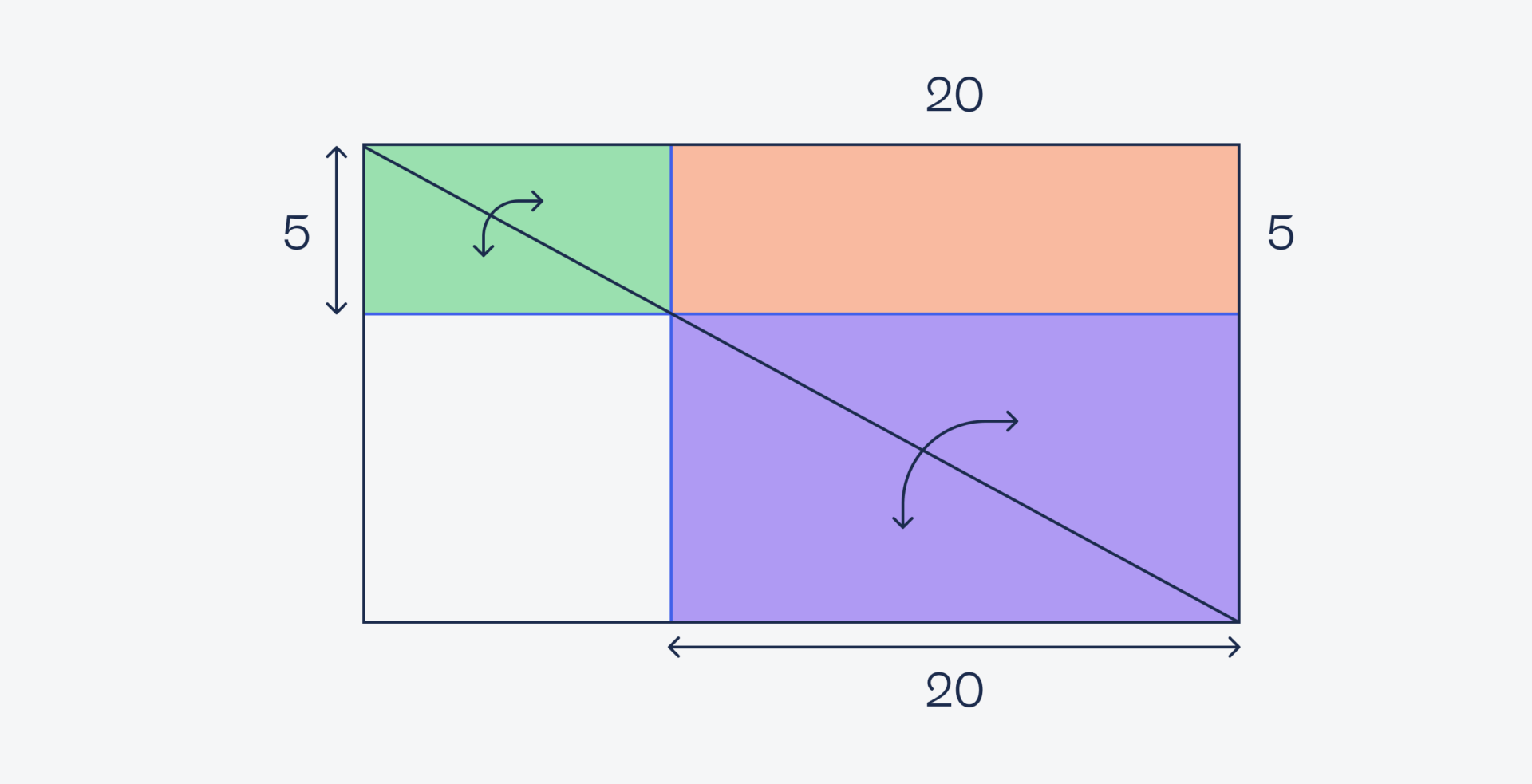
Теперь посмотрим на рисунок так: у нас есть прямоугольник, разделённый пополам по диагонали. Это значит, что площадь нижних треугольников совпадает с площадью верхних треугольников:
Но раз у нас часть площадей в верхнем и нижнем треугольнике одинаковая, их можно вычесть из обеих частей:
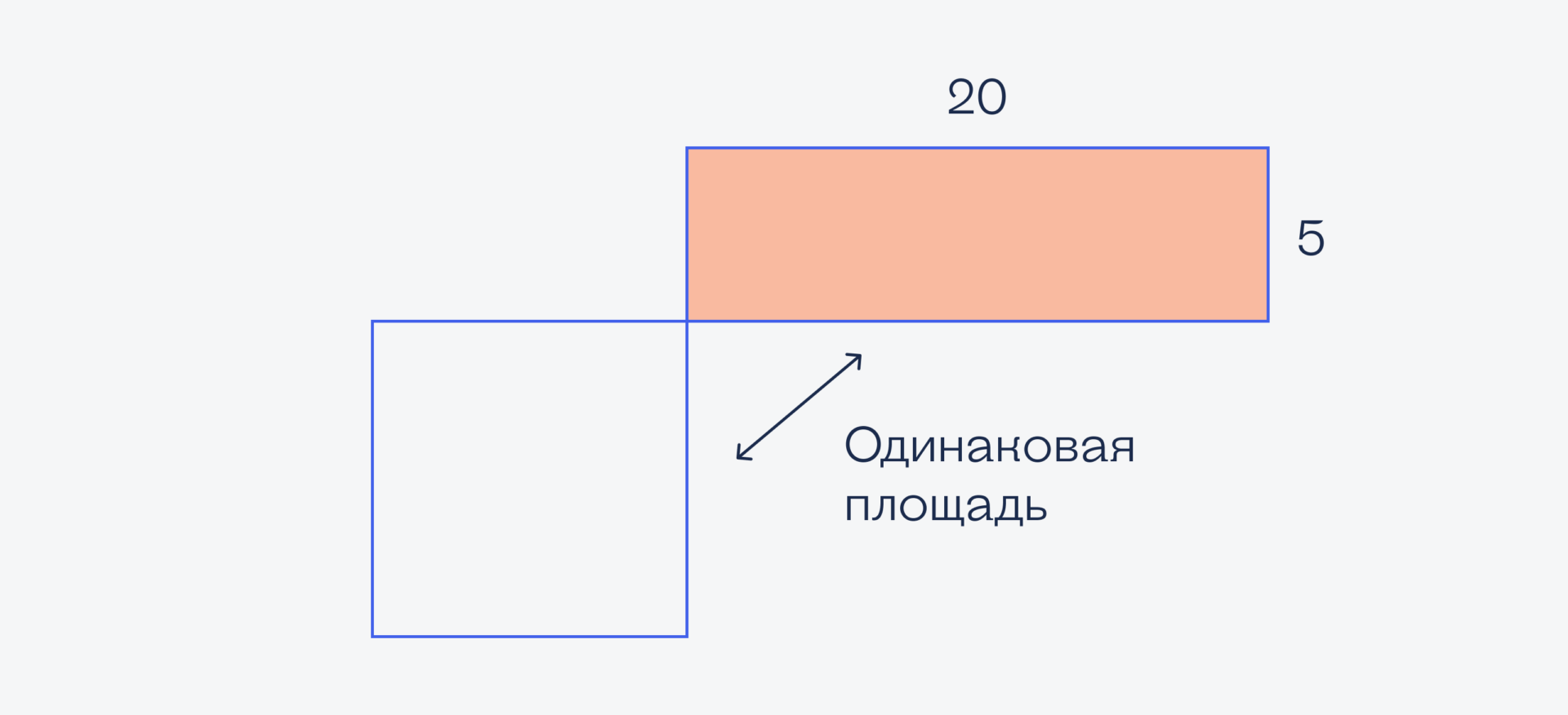
Получается, что площадь оранжевого прямоугольника совпадает с площадью квадрата. А мы знаем, что площадь прямоугольника равна 100; получается, чтобы найти сторону квадрата, нужно извлечь квадратный корень:
√100 = 10
Значит, сторона квадрата равна 10. Этого достаточно, чтобы посчитать всю площадь треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255
Вёрстка:
Кирилл Климентьев
Утверждение
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.
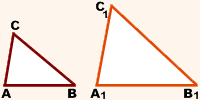
Доказать:
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
Аналогично,
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
то есть
Теперь можем найти, как относятся площади подобных треугольников:
Так как
то
то есть
Что и требовалось доказать.
Поскольку отношение любых линейных размеров (высот, медиан, биссектрис, периметров) подобных треугольников равно коэффициенту подобия, площади подобных треугольников относятся как квадраты их соответствующих линейных размеров.