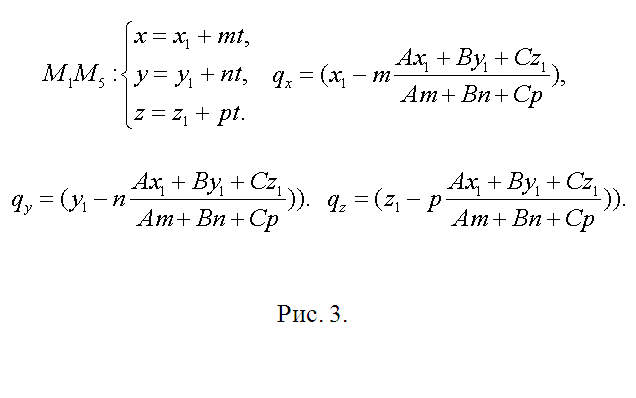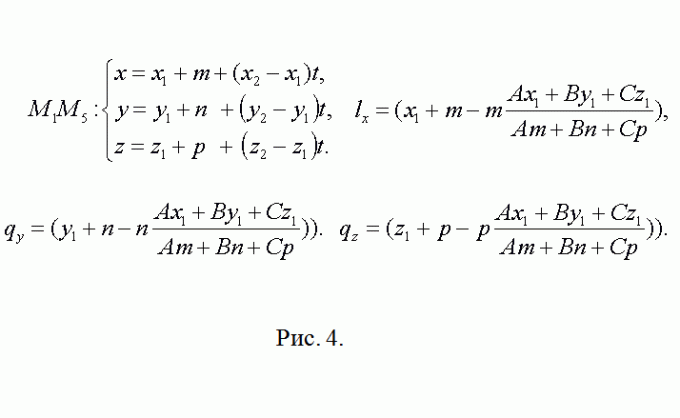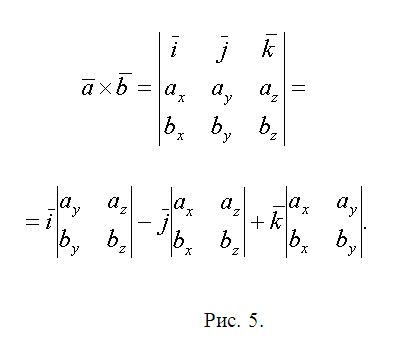Как найти сечение параллелепипеда
Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.
Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов — обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб — это частный случай прямоугольного параллелепипеда.
У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров — площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=√a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.
Периметр диагонального сечения тоже можно вычислять по двум величинам — диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.
Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).
Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b — площадь сечения;
p=2*(a+b).
Пошаговое построение сечения параллелепипеда
Построение сечения методом следов — это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.
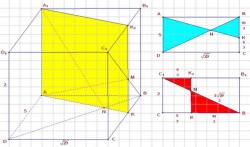
Задача 1.
Построить сечение параллелепипеда плоскостью, проходящей через точки
.
Задача 1. Дано
Шаг 1. Чезез точки и
, которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка
лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой
, которая также принадлежала бы основанию. Для этого проводим прямую
, и находим точку ее пересечения с прямой
—
.
Задача 1. Шаг 1.
Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра
—
.
Задача 1. Шаг 2.
Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой
, которая принадлежала бы плоскости задней грани. Для этого проведем прямую
, которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой
—
. Через две точки задней грани проводим прямую
, и находим место пересечения этой прямой с ребром
—
.
Задача 1. Шаг 3.
Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.
Задача 1. Шаг 4.
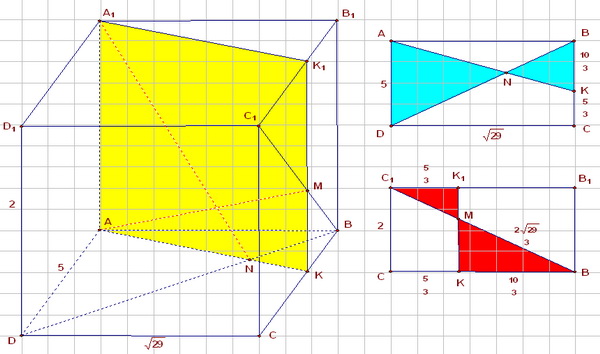
Задача 2.
Построить сечение параллелепипеда плоскостью, проходящей через точки
Задача 2. Дано.
Шаг 1. Точки и
лежат в одной плоскости, можно соединить их прямой. Прямая
пересечет ребро
в точке
.
Задача 2. Шаг 1.
Шаг 2. Точки и
также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра
—
.
Задача 2. Шаг 2
Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч
и найдем его пересечение с прямой
— ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения — точка
. Точки
и
можно соединить отрезком.
Задача 2. Шаг 3.
Шаг 4. Находим точку пересечения отрезком ребра
— точку
.
Задача 2. Шаг 4
Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.
Задача 2. Шаг 5
Задача 3.
Построить сечение параллелепипеда плоскостью, проходящей через точки
Задача 3. Дано.
Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка
принадлежит грани основания, поэтому нужна точка в этой плоскости.
Задача 3. Шаг 1
Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой
—
.
Задача 3. Шаг 2.
Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром
— точка
.
Задача 3. Шаг 3.
Шаг 4. Теперь надо найти точку в плоскости передней грани, потому что в этой плоскости у нас уже есть точка — точка . Для того, чтобы найти такую точку, продлим прямую
и найдем пересечение этой прямой с прямой
— точка
.
Задача 3. Шаг 4
Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер
— точку
, и ребра
— точку
.
Задача 3. Шаг 5.
Шаг 6. Соединяем точки и получаем многоугольник сечения.
Задача 3. Шаг 6
Окончательный вид сечения с другого ракурса:
Окончательный вид
Задача 4.
Построить сечение параллелепипеда плоскостью, проходящей через точки
. Точка
в задней грани.
Задача 4. Дано
Шаг 1. Проводим прямую через две точки одной плоскости — и
. Определяем точку пересечения данной прямой ребра
—
.
Задача 4. Шаг 1.
Шаг 2. Продолжение прямой пересечется с продолжением прямой
— так как обе прямые принадлежат плоскости задней грани. Точка
также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка
, и тогда можно провести прямую
.
Задача 4. Шаг 2.
Шаг 3. Точка — точка пересечения прямой
ребра
. Продлим также ребро
и найдем пересечение прямой
и прямой
— точку
, которая принадлежит плоскости основания.
Задача 4. Шаг 3
Шаг 4. Соединяем Точки и
плоскости основания, определяем точку пересечения данной прямой с ребром
— точку
. Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.
Задача 4. Шаг 4.
Окончательный вид сечения с другого ракурса:
Окончание построения
12 комментариев
Мария
✉️
03.12.2017 15:16:25
Спасибо большое.Все очень доступно изложено,с замечательными иллюстрированными примерами.
Людмила
✉️
20.10.2018 15:37:24
спасибо за желание объяснять:доступно, подробно.
Анна Валерьевна
✨
20.10.2018 15:38:43
Отлично, рада, что пригодилось.
Алексей
✉️
28.10.2018 20:23:47
Вы не разобрали вариант, когда точки T,U,V лежат на разных гранях, скажем, если на рисинке Т лежит на A1B1, U лежит на AD, V лежит на CC1. Что тогда? Действует ли метод? Спасибо
Анна Валерьевна
✨
29.10.2018 07:19:56
Да, действительно, такой случай не рассмотрен. Так как в этом случае более эффективным является метод внутреннего проецирования: https://easy-physic.ru/metod-vnutrennego-proecirovaniya/. Я обещаю сделать в ближайшее время.
Анна Валерьевна
✉️
01.11.2018 15:48:48
Сделала статью. Выйдет, правда, в феврале.
Борис
✉️
05.11.2018 08:09:29
Уважаемая Анна Валерьевна!
Позвольте поблагодарить Вас за интересный и содержательный сайт.
Здоровья Вам, творческих успехов и удачи.
Незнакомец.
Анна Валерьевна
✨
06.11.2018 09:55:33
Спасибо Вам!
Евгений
✉️
06.05.2019 18:39:20
Спасибо за работу.Мне она пригодилась)
LarryGot
✉️
11.04.2022 22:45:45
Jessievob
✉️
14.04.2022 07:02:27
Stevetaind
✉️
17.04.2022 09:45:49
Сечение параллелепипеда: как рассчитать его площадь
Масса задач составлена на основе свойств многогранников. Грани объёмных фигур, как и конкретные точки на них, лежат в разных плоскостях. Если одну из таких плоскостей под определённым углом провести сквозь параллелепипед, то часть плоскости, лежащая в пределах многогранника и разделяющая его на части, будет его сечением.
Вам понадобится
- — линейка
- — карандаш
Инструкция
Постройте параллелепипед. Помните, что его основание и каждая из граней должны представлять собой параллелограмм. Это означает, что вам надо построить многогранник так, чтобы все противоположные рёбра параллельны. Если в условии сказано построить сечение прямоугольного параллелепипеда, то его грани сделайте прямоугольными. У прямой параллелепипед прямоугольные только 4 боковые грани. Если боковые грани параллелепипеда не перпендикулярны основанию, то такой многогранник называют наклонным. Если вы хотите построить сечение куба, изначально начертите прямоугольный параллелепипед с равными размерами. Тогда все шесть его граней будут представлять собой квадраты. Назовите все вершины для удобства обозначения.
Обозначьте две точки, которые будут принадлежать плоскости сечения. Иногда их положение указано в задаче: расстояние от ближайшей вершины, конец отрезка, проведённого по определенным условиям. Теперь проведите прямую через точки, лежащие в одной плоскости.
Найдите прямые на пересечении секущей плоскости с гранями параллелепипеда. Для выполнения этого шага найдите точки, в которых прямая, лежащая в плоскости сечения параллелепипеда, пересекается с прямой линией, принадлежащей грани параллелепипеда. Эти прямые должны находиться в одной плоскости.
Достройте сечение параллелепипеда. При этом помните, что ее плоскость должна пересекать параллельные грани параллелепипеда по параллельным прямым.
Стройте секущую плоскость в соответствии с исходными данными в задаче. Существует несколько возможностей построения плоскости сечения, проходящей:
— перпендикулярно заданной прямой линии через заданную точку;
— перпендикулярно заданной плоскости через заданную прямую;
— параллельно двум скрещивающимся прямым через заданную точку;
— параллельно другой заданной прямой через другую заданную прямую;
— параллельно заданной плоскости через заданную точку.
По таким исходным данным стройте сечение по принципу, описанному выше.
Видео по теме
Обратите внимание
Чтобы построить сечение параллелепипеда, нужно определить точки пересечения плоскости сечения с ребрами параллелепипеда, а затем соединить данные точки отрезками. Учтите, что соединять только те точки, которые лежат в плоскости одной грани. Параллельные грани параллелепипеда пересекайте секущей плоскостью по параллельным отрезкам. Если в плоскости грани только одна точка принадлежит плоскости сечения, постройте дополнительную такую точку. Для этого найдите точки пересечения построенных прямых с теми прямыми, которые лежат в нужных гранях.
Полезный совет
Параллелепипед имеет 6 граней. В его сечениях могут получиться треугольники, четырёхугольники, пятиугольники и фигуры с шестью углами. Плоскость, в том числе и секущая, определяется:
— тремя точками;
— прямой линией и одной точкой;
— двумя линиями, параллельными друг другу;
— двумя прямыми, пересекающимися между собой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Совет 1: Как обнаружить сечение параллелепипеда
Сечения геометрических фигур имеют разные формы. У параллелепипеда сечение неизменно представляет собой прямоугольник либо квадрат. Оно имеет ряд параметров, которые могут быть обнаружены аналитическим методом.
Инструкция
1. Через параллелепипед дозволено провести четыре сечения, которые представляют собой квадраты либо прямоугольники. Каждого он имеет два диагональных и два поперечных сечения. Как водится, они имеют различные размеры. Исключением является куб, у которого они идентичны.Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов – обыкновенный и прямоугольный. У обыкновенного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники либо квадраты. Из этого следует,что куб – это частный случай прямоугольного параллелепипеда.
2. У всякого сечения параллелепипеда есть определенные колляции. Основными из них являются площадь, периметр, длины диагоналей. Если из данные задачи знамениты стороны сечения либо какие-нибудь иные его параметры, этого довольно, дабы обнаружить его периметр либо площадь. По сторонам определяются также диагонали сечений. 1-й из этих параметров – площадь диагонального сечения.Для того дабы обнаружить площадь диагонального сечения, необходимо знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ обнаружьте по теореме Пифагора:d=?a^2+b^2.Обнаружив диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:S=d*h.
3. Периметр диагонального сечения тоже дозволено вычислять по двум величинам – диагонали основания и высоте параллелепипеда. В этом случае сначала обнаружьте две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а после этого сложите с удвоенным значением высоты.
4. Если провести плоскость, параллельную ребрам параллелепипеда, дозволено получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения обнаружьте дальнейшим образом:S=a*h.Периметр этого сечения обнаружьте аналогичным образом по дальнейшей формуле:p=2*(a+h).
5. Конечный случай появляется, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:S=a*b – площадь сечения;p=2*(a+b).
Совет 2: Как обнаружить высоту параллелепипеда
Раньше, чем перейти к нахождению высоты параллелепипеда, необходимо прояснить, что есть высота и что есть параллелепипед. В геометрии, высотой называют перпендикуляр, от вершины фигуры до ее основания либо отрезок, кратчайшим методом соединяющий верхнее и нижнее основания. Параллелепипед – это многогранник, имеющий два параллельных и равных многоугольника в качестве оснований, углы которых объединены отрезками. Параллелепипед составлен из шести параллелограммов, попарно параллельных и равных друг другу.
Инструкция
1. Высоты в параллелограмме может быть три, в зависимости от расположения фигуры в пространстве, чай повернув параллелепипед на бок, вы поменяете местами его основания и грани. Верхний и нижний параллелограммы – неизменно основания. Если боковые ребра фигуры перпендикулярны основаниям, то параллелепипед прямой, и всякое его ребро – готовая высота. Дозволено измерить.
2. Дабы из наклонного параллелепипеда получить прямой, того же размера, нужно продолжить боковые грани в одном направлении. После этого, возвести перпендикулярное сечение, от углов которого, отложить длину ребра параллелепипеда, и на этом расстоянии возвести второе перпендикулярное сечение. Два построенных вами параллелограмма, ограничат новейший параллелепипед, равновеликий первому. На грядущее следует подметить, что объемы равновеликих фигур идентичны.
3. Почаще вопрос о высоте нам встречается в задачах. Неизменно нам даны данные, дозволяющие вычислить её. Это может быть объем, линейные размеры параллелепипеда, длины его диагоналей.Так объем параллелепипеда равен произведению его основания на высоту, то есть, зная объем и размер основания, легко узнать высоту путем деления первого на второе. Если вы имеете дело с прямоугольным параллелепипедом, то есть такие, основание которого прямоугольник, вам могут попытаться усложнить задачу, в связи с его особенными качествами. Так в прямоугольном параллелепипеде, квадрат всякий его диагонали равен сумме квадратов 3 измерений параллелепипеда. Если в «дано» к задаче о прямоугольном параллелепипеде указаны длина его диагонали и длины сторон основания, то этих сведений довольно, дабы узнать размер желанной высоты.
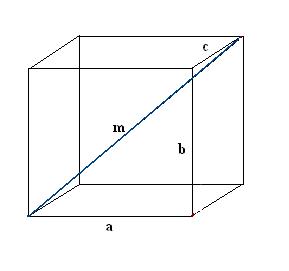
Совет 3: Как обнаружить диагонали параллелепипеда
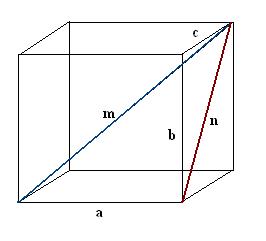
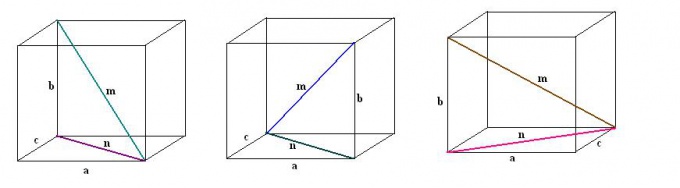
Параллелепипед – частный случай призмы, у которой все шесть граней являются параллелограммами либо прямоугольниками. Параллелепипед с прямоугольными гранями называют также прямоугольным. У параллелепипеда имеется четыре пересекающиеся диагонали. Если даны три ребра а, b, с, обнаружить все диагонали прямоугольного параллелепипеда дозволено, исполняя добавочные построения.
Инструкция
1. Нарисуйте прямоугольный параллелепипед. Запишите вестимые данные: три ребра а, b, с. Сначала постройте одну диагональ m. Для ее определения используем качество прямоугольного параллелепипеда, согласно которому все его углы являются прямыми.
2. Постройте диагональ n одной из граней параллелепипеда. Построение проведите так, дабы вестимое ребро, желанная диагональ параллелепипеда и диагональ грани совместно образовывали прямоугольный треугольник а, n, m.
3. Обнаружьте построенную диагональ грани. Она является гипотенузой иного прямоугольного треугольника b, с, n. Согласно теореме Пифагора n² = с² + b². Вычислите данное выражение и возьмите корень квадратный из полученного значения – это будет диагональ грани n.
4. Обнаружьте диагональ параллелепипеда m. Для этого в прямоугольном треугольнике а, n, m обнаружьте неведомую гипотенузу: m² = n² + a². Подставьте вестимые значения, после этого вычислите корень квадратный. Полученный итог и будет первой диагональю параллелепипеда m.
5. Аналогичным образом проведите ступенчато все остальные три диагонали параллелепипеда. Также для всей из них исполните добавочные построения диагоналей прилегающих граней. Рассматривая образуемые прямоугольные треугольники и применяя теорему Пифагора, обнаружьте значения остальных диагоналей прямоугольного параллелепипеда.
Видео по теме
Совет 4: Как обнаружить объем параллепипеда
Форму параллелепипеда имеют многие настоящие объекты. Примерами являются комната и бассейн. Детали, имеющие такую форму – не редкость и в промышленности. По этой причине зачастую появляется задача нахождения объема данной фигуры.
Инструкция
1. Параллелепипед представляет собой призму, основанием которой является параллелограмм. У параллелепипеда имеются грани – все плоскости, формирующие данную фигуру. Каждого у него насчитывается шесть граней, причем, все они являются параллелограммами. Его противоположные грани между собой равны и параллельны. Помимо того, он имеет диагонали, которые пересекаются в одной точке и в ней делятся напополам.
2. Параллелепипед бывает 2-х видов. У первого все грани являются параллелограммами, а у второго – прямоугольниками. Конечный из них именуется прямоугольным параллелепипедом. У него все грани прямоугольные, а боковые грани перпендикулярны к основанию. Если прямоугольный параллелепипед имеет грани, основы которых – квадраты, то он именуется кубом. В этом случае, его грани и ребра равны. Ребром именуется сторона всякого многогранника, к числу которых относится и параллелепипед.
3. Для того, дабы обнаружить объем параллелепипеда, нужно знать площадь его основания и высоту. Объем находится исходя из того, какой именно параллелепипед фигурирует в условиях задачи. У обычного параллелепипеда в основании находится параллелограмм, а у прямоугольного – прямоугольник либо квадрат, у которого неизменно углы прямые. Если в основании параллелепипеда лежит параллелограмм, то его объем находится дальнейшим образом:V=S*H, где S – площадь основания, H -высота параллелепипедаВысотой параллелепипеда обыкновенно выступает его боковое ребро. В основании параллелепипеда может лежать и параллелограмм, не являющийся прямоугольником. Из курса планиметрии знаменито, что площадь параллелограмма равна:S=a*h, где h – высота параллелограмма, a – длина основания, т.е. :V=a*hp*H
4. Если имеет место 2-й случай, когда основание параллелепипеда – прямоугольник, то объем вычисляется по той же формуле, но площадь основания находится несколько другим образом:V=S*H,S=a*b, где a и b – соответственно, стороны прямоугольника и ребра параллелепипеда.V=a*b*H
5. Для нахождения объема куба следует руководствоваться примитивными логическими методами. От того что все грани и ребра куба равны, а в основании куба – квадрат, руководствуясь формулами, указанными выше, дозволено вывести следующую формулу:V=a^3
Совет 5: Как возвести сечение параллелепипеда
Во многих учебниках встречаются задания, связанные с построением сечений разных геометрических фигур, в том числе параллелепипедов. Для того дабы совладать с такой задачей, следует вооружиться некоторыми познаниями.
Вам понадобится
- – бумага;
- – ручка;
- – линейка.
Инструкция
1. На листе бумаге начертите параллелепипед. Если в вашей задаче сказано, что параллелепипед должен быть прямоугольным, то сделайте его углы прямыми. Помните, что противоположные ребра обязаны быть параллельны друг другу. Назовите его вершины, скажем, S1, T1, T, R, P, R1, P1 (как показано на рисунке).
2. На краю SS1TT1 поставьте 2 точки: А и С, пускай точка А будет на отрезке S1T1, а точка С на отрезке S1S. Если в вашей задаче не сказано, где именно обязаны стоять эти точки, и не указано расстояние от вершин, поставьте их произвольно. Проведите прямую линию через точки А и С. Продолжите эту линию до пересечения с отрезком ST. Обозначьте место пересечения, пускай это будет точка М.
3. Поставьте точку на отрезке RT, обозначьте ее как точку В. Проведите прямую линию через точки М и В. Точку пересечения этой линии с ребром SP обозначьте как точку К.
4. Объедините точки К и С. Они обязаны лежать на одной грани PP1SS1. Позже этого через точку B проведите прямую линию, параллельную отрезку КС, продолжите линию до пересечения с ребром R1T1. Точку пересечения обозначьте как точку Е.
5. Объедините точки А и Е. Позже этого выделите получившийся многоугольник ACKBE иным цветом – это будет сечение заданного параллелепипеда.
Обратите внимание!
Помните, что при построении сечения параллелепипеда дозволено соединять между собой только те точки, которые лежат в одной плоскости, если имеющихся у вас точек неудовлетворительно для построения сечения, достраивайте их, путем продолжения отрезков до пересечения с гранью, на которой надобна точка.
Полезный совет
Каждого в параллелепипеде может быть построено 4 сечения: 2 диагональных и 2 поперечных. Для большей наглядности, выделите получившийся многоугольник-сечение, для этого можете примитивно обвести либо заштриховать его иным цветом.
Совет 6: Как обнаружить длину диагоналей параллелепипеда
Параллелепипедом именуется призма, основанием которой служит параллелограмм. Параллелограммы, из которых составлен параллелепипед, именуются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда.
Инструкция
1. У параллелепипеда дозволено возвести четыре пересекающиеся диагонали. Если знамениты данные 3 ребер а, b и с, обнаружить длины диагоналей прямоугольного параллелепипеда не составит труда, исполняя добавочные построения.
2. Вначале нарисуйте прямоугольный параллелепипед. Подпишите все вестимые вам данные, их должно быть три: ребра а, b и с. Начертите первую диагональ m. Для ее построения воспользуйтесь свойством прямоугольных параллелепипедов, согласно которому все углы сходственных фигур являются прямыми.
3. Постройте диагональ n одной из граней параллелепипеда . Построение сделайте таким образом, дабы знаменитое ребро (а), незнакомая диагональ параллелепипеда и диагональ прилегающей грани (n) образовывали прямоугольный треугольник а, n, m.
4. Посмотрите на построенную диагональ грани (n). Она является гипотенузой иного прямоугольного треугольника b, с, n. Следуя теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов (n? = с? + b?), обнаружьте квадрат гипотенузы, после этого извлеките корень квадратный из полученного значения – это и будет длина диагонали грани n.
5. Обнаружьте диагональ самого параллелепипеда m. Для того, дабы обнаружить ее значение, в прямоугольном треугольнике а, n, m вычислите по той же формуле гипотенузу: m? = n? + a?. Вычислите корень квадратный. Обнаруженный итог будет первой диагональю вашего параллелепипеда . Диагональ m.
6. Верно так же проведите ступенчато все остальные диагонали параллелепипеда , для всей из которых исполняйте добавочные построения диагоналей прилегающих граней. Применяя теорему Пифагора, обнаружьте значения остальных диагоналей данного параллелепипеда .
7. Есть еще один метод, с поддержкой которого дозволено обнаружить длину диагонали. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов 3 его сторон. Из этого следует, что длину дозволено обнаружить сложив квадраты сторон параллелепипеда и из получившегося значения извлечь квадрат.
Полезный совет
Свойства параллелепипеда:- параллелепипед симметричен касательно середины его диагонали;- всякий отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею напополам, в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею напополам;- противолежащие грани параллелепипеда параллельны и равны;- квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Совет 7: Как обнаружить площадь параллелепипеда
Параллелепипед – объемная геометрическая фигура с тремя измерительными колляциями: длиной, шириной и высотой. Все они участвуют в нахождении площади обеих поверхностей параллелепипеда : полной и боковой.
Инструкция
1. Параллелепипед – многогранник, построенный на основе параллелограмма. У него шесть граней, также являющихся этими двухмерными фигурами. В зависимости от того, как они расположены в пространстве, различают прямой и наклонный параллелепипед. Эта разница выражается в равенстве угла между основанием и боковым ребром 90°.
2. По тому, к какому частному случаю параллелограмма относится основание, дозволено выделить прямоугольный параллелепипед и особенно распространенную его разновидность – куб. Эти формы особенно зачастую встречаются в повседневной жизни и носят наименование стандартных. Они присущи бытовой технике, предметам мебели, электронным приборам и др., а также самим человеческим жилищам, размеры которых имеют весомое значение для обитателей и риелторов.
3. Обыкновенно считают площадь обеих поверхностей параллелепипеда , боковой и полной. Первая числовая колляция представляет собой общность площадей его граней, вторая – та же величина плюс площади обоих оснований, т.е. сумма всех двухмерных фигур, из которых состоит параллелепипед. Следующие формулы носят наименование основных наравне с объемом:Sб = Р•h, где Р – пeримeтр основания, h – высота;Sп = Sб + 2•S, где So – площадь основания.
4. Для частных случаев, куба и фигуры с прямоугольными основаниями, формулы упрощаются. Сейчас теснее не надобно определять высоту, которая равна длине вертикального ребра, а площадь и периметр обнаружить значительно легче вследствие наличию прямых углов, в их определении участвуют только длина и ширина. Выходит, для прямоугольного параллелепипеда :Sб = 2•с•(a + b), где 2•(а + b) – удвоенная сумма сторон основания (периметр), с – длина бокового ребра;Sп = Sб + 2•а•b = 2•а•с + 2•b•с + 2•a•b = 2•(а•с + b•с + а•b).
5. У куба все ребра имеют идентичную длину, следственно:Sб = 4•а•а = 4•а?;Sп = Sб + 2•а? = 6•а?.
Совет 8: Как обнаружить площадь сечения куба
Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры. Могут потребоваться методы рения систем линейных уравнений.
Инструкция
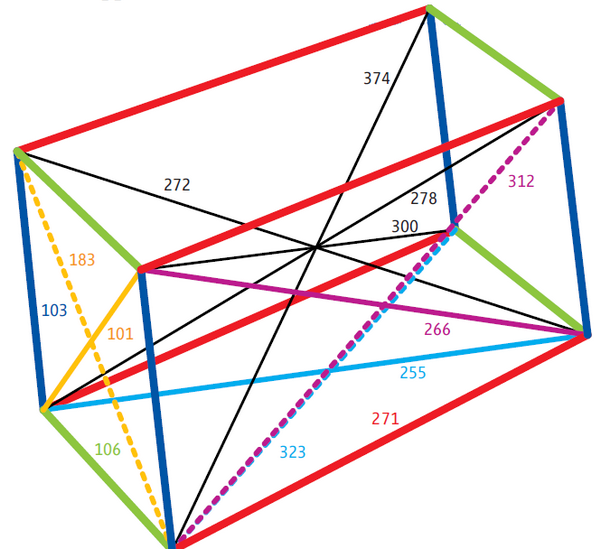
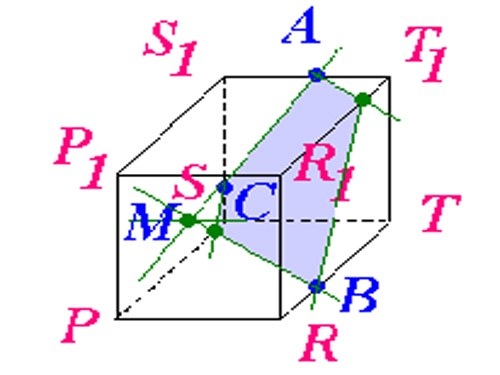
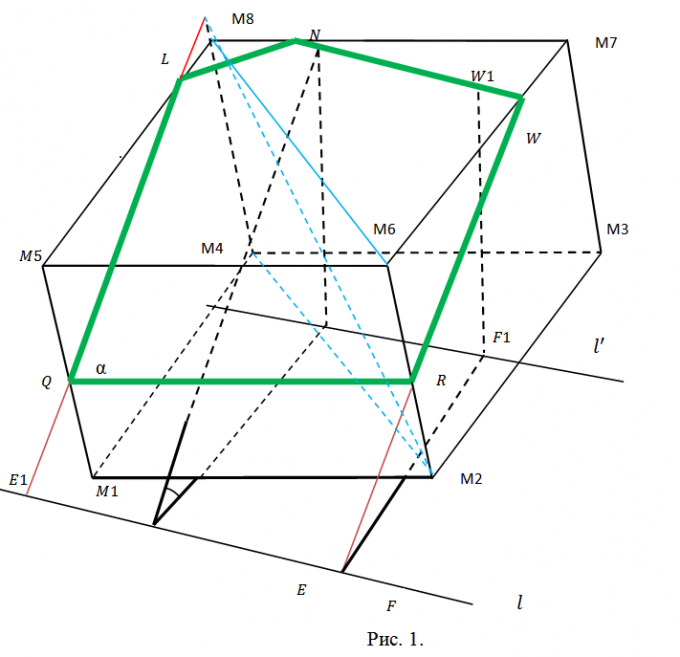
1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость ? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.
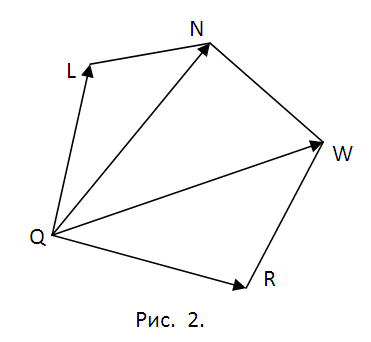
2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью ?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всего из них с подмогой свойств векторного произведения. Методология всякий раз одна и та же. Следственно дозволено ограничиться точками Q и L и площадью треугольника ?QLN.
3. Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), обнаружьте как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=[M1M2? M2M3]. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба обнаружьте как, скажем, ?=?( (x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).
4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.
5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь ?QLN S1=(1/2)|[QL? QN]|. Следуйте предложенной методике и вычислите площади треугольников ?QNW и ?QWR – S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.
Совет 9: Как обнаружить площадь диагонального сечения призмы
Призма — это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в числе, равном числу сторон многоугольника основания.
Инструкция
1. В произвольной призме боковые ребра расположены под углом к плоскости основания. Частным случаем является прямая призма. В ней боковые стороны лежат в плоскостях, перпендикулярных основаниям. В прямой призме боковые грани — прямоугольники, а боковые ребра равны высоте призмы.
2. Диагональное сечение призмы — часть плоскости, всецело заключенная во внутреннем пространстве многогранника. Диагональное сечение может быть ограничено двумя боковыми ребрами геометрического тела и диагоналями оснований. Видимо, что число допустимых диагональных сечений при этом определяется числом диагоналей в многоугольнике основания.
3. Либо границами диагонального сечения могут служить диагонали боковых граней и противоположные стороны оснований призмы. Диагональное сечение прямоугольной призмы имеет форму прямоугольника. В всеобщем случае произвольной призмы форма диагонального сечения – параллелограмм.
4. В прямоугольной призме площадь диагонального сечения S определяется по формулам:S=d*Hгде d — диагональ основания, H — высота призмы.Либо S=a*Dгде а — сторона основания, принадлежащая единовременно плоскости сечения, D — диагональ боковой грани.
5. В произвольной непрямой призме диагональное сечение — параллелограмм, одна сторона которого равна боковому ребру призмы, иная – диагонали основания. Либо сторонами диагонального сечения могут быть диагонали боковых граней и стороны оснований между вершинами призмы, откуда проведены диагонали боковых поверхностей. Площадь параллелограмма S определяется формулой: S=d*hгде d — диагональ основания призмы, h — высота параллелограмма — диагонального сечения призмы.Либо S=a*hгде а — сторона основания призмы, являющаяся и рубежом диагонального сечения, h — высота параллелограмма.
6. Для определения высоты диагонального сечения неудовлетворительно знать линейные размеры призмы. Нужны данные о наклоне призмы к плоскости основания. Последующая задача сводится к ступенчатому решению нескольких треугольников в зависимости от начальных данных об углах между элементами призмы.