
плотин, либо других гидротехнических сооружений, представляющих собой препятствие для свободного тока воды.
Для построения зоны затопления исходной величиной является абсолютная высота плотины или подпорного сооружения, а также положение самой плотины 1-2 на местности. Абсолютная высота плотины задает абсолютную высоту горизонтали (рис. 2.27), которую сравнительно легко провести между горизонталями, имеющимися на карте.
Граница зоны затопления показывает на карте местность, покрывающуюся водой после строительства плотины, что необходимо для принятия соответствующих предупредительных мер. Кроме того, использование горизонталей карты и отметки водного зеркала позволяет решить задачу о емкости водохранилища.
Существует несколько способов определения площадей: аналитический, графический и механический.
Аналитический метод заключается в определении площади земельного участка по результатам непосредственных или косвенных измерений линий, углов. Если площади земельных участков представляют собой простые геометрические фигуры (треугольники, многоугольники и т.п.), то их площадь определяют аналитически по размерам сторон треугольников, на которые следует разбить более сложные геометрические фигуры. В этом случае, если известны основания аi и высоты hi, то площадь S многоугольника определяется как сумма нескольких треугольников (рис. 2.28 б):
i= n
S = 0,5å ai hi
i= 1
(2.29) Если в треугольнике известны все стороны a, b и с, то для вычисления
площади можно воспользоваться другой формулой
S = 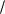
(2.30)
где Р – полупериметр треугольника.
Если в треугольнике известны две стороны а и b и угол между ними β, то площадь находится по формуле
S = 0,5ab sin β
(2.31) Площадь треугольника может быть найдена также и по известной сторо-
не а и двум углам α и β, прилежащим к ней:
|
S = |
a 2 |
|
2(ctg α + ctg β ) |
(2.32) Если известны прямоугольные координаты вершин многоугольника
(рис. 2.28 а), то значение его площади может быть получено по формуле:
60

S = 0,5[ X1 (Y2 − Yn ) + X 2 (Y3 − Y1 ) + … + X n (Y1 − Yn−1 )]
(2.33)
или
S = 0,5[Y1 (X 2 − X n ) + Y2 (X 3 − X1 ) + … + Yn (X1 − X n− 1 )]
(2.34) Т.е. удвоенная площадь полигона равна сумме произведений абсциссы (ординаты) каждой из точек на разность ординат последующей и преды-
дущей (абсцисс последующей и предыдущей) точек.
Рис. 2.28. Аналитичесий (а) и графический (б) способы определения площади многоугольника
В зависимости от направления обхода значение площади может получиться со знаком минус. В связи с этим площадь надо брать по абсолютной величине.
Вычисление площади многоугольника по координатам его вершин следует выполнять для контроля по формулам (2.33) и (2.34).
Пример 2.17. Определение площади полигона по координатам его вершин. Исходные данные
|
Точки |
1 |
2 |
3 |
4 |
|
Х, м |
2156,847 |
1921,315 |
1541,242 |
1756,211 |
|
Y, м |
4600,212 |
4563,842 |
4781,747 |
4763,226 |
Решение.
S = 0,5 [2156,847(4563,842 – 4763,226) + 1921,315(4781,747 – 4600,212) + 1541,242 (4763,226 – 4563,842) + 1756,211(4600,212 – 4781,747)] = 0,5[2156,847 (-199,384) + +1921,315 (181,535) + 1541,242(199,384) + 1756,211(-181,535)] = 46384,816 м2.
S = 0,5 [4600,212(1921,315 – 1756,211) + 4563,842(1541,242 – 2156,847) + 4781,747 (1756,211 – 1921,315) + 4763,226(2156,847 – 1541,242)] = 0,5[4600,212 (165,104) + +4563,842 (-615,605) + 4781,747(-165,104) + 4763,226(615,605)] = 46384,816 м2.
Ответы совпали !
Графический и механический методы используются для определения площадей на картографических изображениях.
61

Графический метод (рис. 2.28 б) предусматривает измерение на плане элементов сравнительно простых фигур (треугольника, прямоугольника, трапеции и др.), позволяющих затем вычислить площадь. Сложные фигуры разбивают обычно на треугольники, в которых измеряют основание и высоту. В некоторых случаях и площади криволинейного контура также разбивают на треугольники или другие простые фигуры.
Фигуры, на которые производят разбивку площадей объектов, должны быть по возможности крупными, мало вытянутыми, большая точность будет достигаться, например, при основании треугольника, равном его высоте, опущенной на это основание.
Часто в пределах измеряемой площади есть линии или углы, величины которых известны из результатов непосредственных измерений на местности. В этом случае необходимо разбивку привязать к этим линиям или углам, и использовать известные данные при вычислении площади.
Для повышения точности площадь фигуры следует определять не менее двух-трех раз, причем следует использовать разные разбивки. Расхождение в результатах определения площади по нескольким разбивкам не должно превышать 1:50 от величины площади всего участка.
Рис. 2.29. Определение площади фигуры с помощью палеток а – квадратная палетка; б – линейная палетка; в – точечная палетка
Механический метод определения площадей предусматривает использование палеток, ротометров, планиметров или других приборов.
Определение площадей с помощью палеток. Принцип определения площади с помощью палетки пояснен на рис. 2.29. Палетка представляет собой прозрачную основу, на которой построена сетка квадратов с известной стороной (квадратная палетка), серия параллельных линий с известным расстоянием между ними (линейная палетка), упорядоченная группа точек с известными расстояниями между ними (точечная палетка).
При использовании квадратной палетки для данного картографического материала определяют площадь элементарной ячейки (квадрата). Например, сторона квадрата равна 2 мм, масштаб карты 1:10000. В этом случае сторона квадрата на местности будет равна 20 м, а площадь – 400 м2. Палетку накладывают произвольно на фигуру и определяют число полных квадратов (N) и число всех неполных квадратов (n). Площадь определяют по формуле
62

|
S = 0,5 ( 2N + n ) S0 |
(2.35) |
Пример 2.18. Определение площади с помощью квадратной палетки. Исходные данные (рис. 2.29 а) : N = 107, n = 49.
Решение.
S = 400 (107 + 49/2) = 52600 м2 (при S0 = 400 м2).
Похожий принцип реализуется и при использовании линейной палетки (рис. 2.29 в). В качестве единичной площади здесь выступает элементарная полоса длиной lo , например, 1 см при известном расстоянии а между линиями. В пределах контура фигуры измеряют длины линий посредине между нанесенными на палетку параллельными линиями, суммируют их и переводят через значение S0 в площадь. Если крайние границы контура образуют криволинейный треугольник, как это получилось на рисунке, то величину измеренного отрезка делят пополам. Т.е. площадь определяется в этом случае так же, как и площадь треугольника. В примере, который приведен ниже, это учтено для соответствующих отрезков.
Пример 2.19. Определение площади с помощью линейной палетки.
Исходные данные (результаты измерения в пределах контура криволинейной фигуры): (9,0:2 + 17,2 + 22,4 + 24,6 + 25,0 + 25,8 + 27,0 + 27,0 + 27,2 + 29,3 + 28,0 + 28,0 + 28,5 + 25,0 + 9,4:2 ) мм = 344,2 мм = 34,42 см.
Площадь определяется на карте 1:5000. Расстояние между линиями палетки 2 мм. Длина единичного отрезка принята равной 1 см. Следовательно, единичная площадь
Sо = 50 м · 10 м = 500 м2.
Решение.
S = (500 · 34,42) = 17210 м2.
При использовании точечной палетки (рис. 2.29 б) определяют площадь зоны влияния каждой точки, которая, вообще говоря, равна площади квадрата, как и в квадратной палетке. В контуре подсчитывают число точек (N) и умножают его на значение элементарной площади. При этом рекомендуется не принимать во внимание точки, совпадающие с контуром измеряяемой площади.
Пример 2.20. Определение площади с помощью точечной палетки. Исходные данные: Sо = 200 м2. N = 87 (рис. 2.29 б).
Решение.
S = 200 · 87 = 17400 м2.
Для повышения точности площадь определяют несколько раз (5 – 6 раз) с произвольной перестановкой используемой палетки в любое положение в том числе и с поворотом относительно ее первоначального положения. За окончательное значение площади принимают среднее арифметическое из результатов измерений.
Более точным и простым в использовании является способ линейной палетки, в котором суммируются отрезки палетки, пересекающие контур.
Определение площадей с помощью планиметра (рис. 2.30).
Планиметр был изобретен в 1850 г. русским конструктором П.А.Зарубиным.
63

Планиметр – это механический прибор, состоящий из полюсного рычага 1 с грузиком 3. Грузик содержит в центре иглу для закрепления его в устойчивом положении на столе. На другом конце полюсного рычага имеется сферическая шарнирная головка, которая свободно вставляется в гнездо 5 обводного рычага 2. На обводном рычаге имеется обводной штырь (игла) 4 и счетный механизм 6. Счетный механизм имеет дисковую шкалу 7 счета оборотов, счетное колесо 8, один оборот которого соответствует одному делению дисковой шкалы. Внешний ободок счетного колеса скользит по бумаге и за счет трения проворачивается и приводит в движение через червячную передачу дисковую шкалу. Со шкалой счетного колеса сопряжена шкала нониуса 9, по которой берут отсчет дробной части наименьшего деления шкалы счетного колеса.
Рис. 2.30. Планиметр 1- полюсный рычаг; 2 – обводной рычаг; 3 – груз; 4 – игла; 5 – гнездо; 6 – счетный
механизм; 7 – дисковая шкала; 8 – счетное колесо; 9 – нониус.
Полный отсчет (рис. 2.30) содержит четыре значащих цифры: 1-я – отсчет по шкале диска (3); 2-я – подписанное число на дисковой шкале до нулевого индекса нониуса (5); 3-я – число полных наименьших делений от ближайшей по возрастанию подписанной цифры счетного колеса до нулевого индекса нониуса (8); 4-я – ближайшее от нулевого индекса нониуса деление, совпа-дающее с делением шкалы счетного колеса (2). Таким образом, отсчет равен 3582.
Последовательность измерения площади фигуры.
1. Установить планиметр на карте таким образом, чтобы при обводе фигуры угол между полюсным и обводным рычагом не был меньше 30о и больше 150о. При этом колесо счетного механизма обязательно должно перемещаться по поверхности бумаги. Если фигура большая, т.е. не обеспе-
64
чивается поставленное выше условие, то ее следует измерять по частям. После подбора установки планиметра закрепить полюс нажатием на грузик и
вдальнейшем при измерениях не смещать.
2.Установить обводную иглу в точку фигуры, имеющей известную площадь и находящейся примерно в том же месте, что и измеряемая площадь. Такой фигурой может быть один, два или несколько квадратов километровой сетки системы прямоугольных координат карты. Если на картографическом материале отсутствуют фигуры известной площади, то можно их построить. Например, окружность известного радиуса, треугольник, квадрат и т.п. Взять начальный отсчет Ао по шкалам счетного устройства (например, Ао = 5783).
3.Аккуратно обвести фигуру с известной площадью с возвращением в начальную точку. Взять отсчет Во (например, Во = 5648).
4.Установить обводную иглу в точку фигуры с неизвестной площадью и взять начальный отсчет А (например, А = 4277).
5.Аккуратно обвести фигуру с неизвестной площадью с возвращением в начальную точку. Взять отсчет В (например, В = 4203).
6.Вычислить разности отсчетов
Со=Ао— Во и С = А – В: Со = 5783 – 5648 = 135; С = 4277 – 4203 = 74.
7. Вычислить площадь фигуры. Предположим, что известная площадь Sо
|
2 |
æ |
SO C |
ö |
||
|
(Sо = 4 км ), тогда |
S |
= |
ç |
||
|
ç |
CO |
. |
|||
|
è |
ø |
||||
|
В приведенном примере: S = (4 км2 · 74) : 135 = 2,193 км2. |
|||||
|
Отношение Sо |
/ Со = μ называется ценой деления планиметра. Таким |
||||
|
образом, S = μС. |
Для повышения точности измерений площадь определяют несколько раз по схеме, приведенной выше. Целесообразно обвод площадей (известной и неизвестной) выполнять по часовой и против часовой стрелки, т.е. один полный прием измерения площади будет заключаться в двойном измерении. Обычно достаточно двух полных приемов. Окончательное значение площади находят как среднее арифметическое из результатов полных приемов измерений.
Если планиметр содержит два отсчетных устройства, то достаточно выполнить один полный прием, но при использовании во всех случаях двух отсчетных устройств, т.е. по каждой из точек брать по два отсчета, например,
Ао1, Ао2, Во1, Во2, А1, А2 и т.д.
До начала работы с планиметром необходимо выполнить его поверки в соответствии с указаниями, приводящимися в инструкции по пользованию, либо в другой соответствующей литературе.
При решении различных задач требования к точности определения площадей различные. В связи с этим в каждом случае требуется выбирать и способ определения площади.
В настоящее время выпускаются планиметры различных конструкций, в том числе и электронные планиметры, выдающие результаты измерений на механическое или электронное табло. На рынке геодезических приборов
65
Чтобы произвести измерение расстояний потопографической карте, пользуются численным, линейным или поперечным масштабом. Расстояния между точками на топографической карте обычно измеряются циркулем-измерителем или курвиметром.
Измерение расстояний и определение площадей по топографической карте, численный, линейный и поперечный масштаб.
Численный масштаб топографической карты.
Это масштаб карты выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее степень уменьшения на карте линий местности. Чем меньше знаменатель масштаба, тем крупнее масштаб карты. Подпись численного масштаба на картах обычно сопровождается указанием величины масштаба – расстояния на местности (в метрах или километрах), соответствующего одному сантиметру карты.
Например 1:50 000 – в 1 сантиметре 500 метров. Величина масштаба в метрах соответствует знаменателю численного масштаба без двух последних нулей. При определении расстояния с помощью численного масштаба линия на карте измеряетсялинейкой, полученный результат в сантиметрах умножается на величину масштаба.
Линейный масштаб топографической карты.
Линейный масштаб – графическое выражение численного масштаба. Он представляет собой прямую линию, разделенную на определенные части, которые сопровождаются подписями, означающими расстояния на местности.
Поперечный масштаб топографической карты.
Поперечный масштаб – график (обычно на металлической пластинке) для измерения и откладываниярасстояний на карте с предельной графической точностью (0,1 мм). Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм. Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй – 0,4 мм, по третьей – 0,6 мм и т. д.
С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба. Отсчет расстояния по поперечномумасштабу состоит из суммы отсчета на основании графика и отсчета отрезка между вертикальной и наклонной линиями. На рисунке выше, расстояние между точками А и В (при масштабе карты 1:100 000) равно 5500 метров (4 км + 1400 м + 100 м).
Измерение расстояний на карте циркулем–измерителем.
При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратамкоординатной сетки, а остаток – обычным порядком по масштабу.
Измерение расстояний на карте способом наращивания раствора циркуля.
Измерение расстояний на карте шагом циркуля.
Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками. Измерение расстояний и длин кривых линий производится последовательным отложением шага циркуля. Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.
Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой. Поэтому в результаты измерений покарте приходится вводить поправку – коэффициенты увеличения расстояний.
Измерение расстояний на карте курвиметром.
Вращением колесика стрелкукурвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии с равномерным нажимом слева направо или снизу вверх. Полученный отсчет в сантиметрах умножают на величину масштаба данной карты.
Определение расстояний по прямоугольным координатам точек.
Определение расстояний попрямоугольным координатам точек в пределах одной зоны карты можно произвести по формуле
где D – длина линии, x1, y1 – координаты начальной точки прямой, x2, y2 – координаты конечной точки прямой.
Определение площадей по квадратам километровой сетки карты.
Площадь участка определяется подсчетом целых квадратов и их долей, оцениваемых на глаз. Каждому квадрату километровой сетки соответствует: на картах масштаба 1:25 000 и 1:50 000 – 1 км2, на картах масштаба 1:100 000 – 4 км2, на картах масштаба 1:200 000 – 16 км2.
По материалам книги Способы автономного выживания человека в природе.
Под редакцией Л. А. Михайлова.
Суть практических работ по топографии заключается в том, что студенты, изучив теоретический материал, выполняют практические задания по формированию соответствующих умений и навыков работы с топографической картой. Часть практических работ выполняется индивидуальными заданиями: ориентирование, определение направлений движения по заданным азимутам, составление плана местности, определение относительной высоты холма, скорости течения реки, измерение длин линий по прямой и кривой и др. Практические работы с топографическими картами формируют навыки сложного чтения карты, позволяют, в будущем, анализировать географические явления, составлять физико-географические и экономико-географические характеристики отдельных участков или районов, давать оценку территории по заданным критериям [1, 2].
Определение площади карты и плана, как и отдельных контуров на нем имеет практическое значение. В результате вычисления площадей составляется экспликация угодий (перечень угодий с указанием их площади), производится организация территории и решается ряд других задач. Площади вычисляются различными способами.
Аналитический метод состоит в определении площади участка по результатам непосредственных измерений линий и углов в натуре или по координатам вершин (граничных точек). Точность величины площади участка при этом зависит только от ошибок измерения длин и углов на местности и характеризуется относительной ошибкой 1/500–1/1000. Однако в условиях большой контурности и вкрапливаний одних контуров в другие, площади которых определяются менее точными способами, аналитический метод становится нецелесообразен.
Аналитический способ основан на использовании результатов полевых измерении (длин линий и углов) и является наиболее точным. При этом используются формулы геометрии, тригонометрии и аналитической геометрии.
Графический метод заключается в том, что данные для вычисления площадей берутся с плана, графически, и площади отдельных геометрических фигур вычисляются с помощью геометрических формул. При графическом способе участок разбивают на треугольники, трапеции и другие фигуры, площадь которых можно вычислить, используя формулы геометрии. Для того чтобы повысить точность вычислений и избежать возможных грубых ошибок, площадь каждой фигуры вычисляют дважды и затем берут среднее (у треугольников разные стороны принимают за основания и к ним проводят высоты). Расхождения между результатами не должны превышать 1/100 (1 %) от площади вычисляемой фигуры.
Расстояния на плане определяются масштабной линейкой или выверенными линейками со скошенными краями. Точность таких измерений должна быть не ниже 2 мм. Точность определения линий на плане прямо пропорциональна их длине, так как короткие и длинные линии вычисляют с одной и той же абсолютной ошибкой (0,2 мм).
Если участок представляет собой многоугольник, то его делят на треугольники, прямоугольники или трапеции. С помощью измерителя и масштабной линейки определяют те величины, которые нужны для получения площадей отдельных фигур. Сумма площадей элементарных геометрических фигур даст общую площадь участка.
Точность определения площади графическим способом зависит от графической ошибки измерения отрезка на плане. Отрезок на плане циркулем — измерителем определяется с ошибкой +0,1 мм, которая не зависит от длины линии. Из этого следует, что относительная ошибка короткой линии больше, а длинной — меньше.
Правила для определения площади графическим способом:
- Площади определяются дважды (либо участок разбивается на другие элементарные фигуры, либо в треугольниках изменяются основания и высота).
- План берется в наиболее крупном масштабе.
- Фигуры должны быть как можно крупнее и не очень вытянуты, то есть основание и высота должны быть примерно равны.
- Если в геометрических фигурах есть линии, величины которых известны из непосредственных измерений, то их надо использовать для вычисления площадей.
- Предельное расхождение двукратных определений не должно превышать1:200 величины площади участка.
При работе по этому способу применяют специальные палетки для проведения высот.
Графически вычисляют площади контуров имеющих вытянутую форму (дорога, канал, ручей и т. д.), ширина которых не всегда выражается в масштабе плана, но она должна быть известна или подписана на плане.
Определение площадей палетками (механический способ). Для определения площадей небольших участков (обременения и сервитутов) по топографическим планам и картам применяют квадратные и параллельные прямоугольные палетки.
Квадратная палетка. Квадратная палетка представляет собой прозрачный лист целлулоида, стекла или восковки, на котором нанесена сеть квадратов со сторонами от 1 до 10 мм. Зная сторону квадрата, легко подсчитать площадь его применительно к любому масштабу плана. Для определения площади палетку накладывают на контур ABCD, имеющийся на плане. Вначале подсчитывают число полных квадратов, а затем неполные квадраты объединяют и глазомерно заменяют некоторым числом полных. Пусть таких квадратов девять. Произведение площади одного квадрата на число их даст площадь определяемого участка. Например, в криволинейном контуре на плане масштаба 1: 500 оказалось 58,5 клеток палетки со стороной квадрата 2 мм. В одном квадрате содержится площадь в 1 м2, следовательно, площадь определяемого контура будет равна 1 м2 * 58,5 клеток = 58,5 м2. Для упрощения подсчетов проводят утолщение линии через 1 см, чтобы число целых клеток можно было подсчитать сразу группами (по 25 мм2). Точность определения площади квадратной палеткой не превышает 1:100.
Недостаток квадратной палетки заключается в том, что площади долей клеток оцениваются на глаз, а подсчет целых клеток может сопровождаться ошибками, поэтому не рекомендуется такой палеткой определять площади больше 2 см2 на плане. Отмеченных выше недостатков квадратной палетки не наблюдается при определении площадей параллельной палеткой, представляющей собой лист прозрачного материала, на котором нанесены параллельные линии, в основном через 2 мм одна от другой.
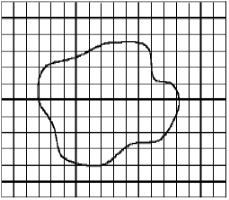
Рис. 1. Квадратная палетка
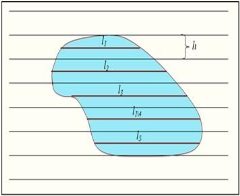
Рис. 2. Параллельная палетка
Палетки с параллельными линиями. Палетка с параллельными линиями отличается от квадратной тем, что вместо квадратов на ней наносятся параллельные линии. На ней нанесены параллельные линии с интервалом в 2 мм. Для определения площади участка палетку накладывают на контур плана так, чтобы наиболее удаленные друг от друга точки, например, приходились на середину расстояния между какими-либо параллельными линиями. В результате этого площадь определяемого контура будет разбита на трапеции, у которых сплошные линии будут средними линиями трапеций, а пунктирные (на палетке отсутствуют) — основаниями трапеций [3, 4].
Так как высоты трапеций одинаковы и заранее известны, то для получения площади контура надо измерить циркулем средние линии трапеций. Произведение суммы средних линий на расстояние между нитями даст общую площадь контура. При этом надо учитывать масштаб плана.
Чтобы не производить вычислений, ниже палетки наносят шкалу в виде простого линейного масштаба. Ее строят с учетом следующих соображений. При масштабе плана 1:10 000 расстоянию между нитями на палетке в 2 мм соответствует 20 м на местности, следовательно, каждому сантиметру длины полосы на плане будет в натуре соответствовать площадь в 0,2 га. Если на прямой отложить несколько отрезков по 1 см, сделать соответствующие подписи и один отрезок разделить на мелкие части, то достаточно к такой шкале приложить раствор циркуля, соответствующий сумме средних линий трапеций. Прочитанный отсчет по шкале даст площадь в гектарах.
Аналогично этому может быть построена шкала и для другого масштаба. Так, для масштаба 1: 25 000 целесообразно за основание шкалы взять отрезок в 0,8 см, что будет соответствовать 1 га.
Измерение площади участка с криволинейным контуром (криволинейная палетка). Объект с криволинейным контуром разбивают на геометрические фигуры, предварительно спрямив границы с таким расчетом, чтобы сумма отсеченных участков и сумма избытков взаимно компенсировали друг друга. Результаты измерений будут, в некоторой степени, приближенными.
Рис. 3. Спрямление криволинейных границ участка и разбивка на простые геометрические фигуры
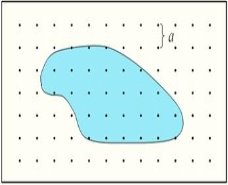
Рис. 4. Точечная палетка
Помимо квадратных палеток, применяют точечные палетки, представляющие собой прозрачные пластины с награвированными точками. Точки ставятся в одном из углов ячеек сеточной палетки с известной ценой деления, затем линии сетки удаляют. Вес каждой точки равен цене деления палетки. Площадь измеряемого участка определяют путем подсчета количества точек, оказавшихся внутри контура, и умножают это количество на вес точки [3, 4].
Измерение площадей значительных участков производится по картам с помощью планиметра. Планиметр служит для определения площадей механическим способом. Широкое распространение имеет полярный планиметр. Он состоит из двух рычагов — полюсного и обводного.

Рис. 5. Полярный планиметр
Определение площади контура планиметром сводится к следующим действиям. Закрепив полюс и установив иглу обводного рычага в начальной точке контура, берут отсчет. Затем обводной шпиль осторожно ведут по контуру до начальной точки и берут второй отсчет. Разность отсчетов даст площадь контура в делениях планиметра. Зная абсолютную цену деления планиметра, определяют площадь контура.
Литература:
- Гакаев Р. А. Статистические методы освоения географических дисциплин бакалавров по направлению подготовки «География». Педагогика высшей школы. 2015. № 2 (2). С. 31–35.
- Гакаев Р. А. Методы картографического исследования и этапы их формирования. Педагогика высшей школы. 2016. № 1 (4). С. 1–4.
- Гакаев Р. А. Точность и погрешность измерений на картах при выполнении практических работ по топографии. Педагогика высшей школы. 2016. № 1 (4). С. 48–53.
- Жмойдяк Р. А. и др. Лабораторные занятия по топографии с основами геодезии. Учебное пособие для географических факультетов / Р. А. Жмойдяк, В. Я. Крищанович, Б. А. Медведев / Мн.: Высш. школа, 1979. — 295 с., ил.





