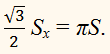Как рассчитать площадь усеченного конуса
На данной странице калькулятор поможет рассчитать площадь поверхности усеченного конуса онлайн. Для расчета задайте радиусы и образующую.
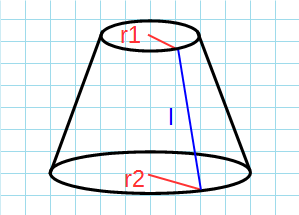
Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образующая конуса — это отрезок, соединяющий вершину и границу основания.
Боковая поверхность
Формула площади боковой поверхности усеченного конуса через радиусы и образующую:
π — константа равная (3.14); r1 — радиус верхнего основания ; r2 — радиус нижнего основания; l — образующая усеченного конуса.
Полная поверхность

Формула площади полной поверхности усеченного конуса через радиусы и образующую:
π — константа равная (3.14); r1 — радиус верхнего основания ; r2 — радиус нижнего основания; l — образующая усеченного конуса.
Площадь поверхности усеченного конуса
-
Площадь боковой поверхности усеченного
конуса равна разности площадей боковых
поверхностей полного конуса и конуса,
отсекаемого плоскостью, параллельной
основанию конуса.
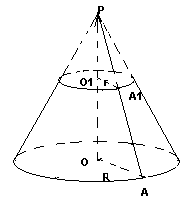
Пусть Р – вершина конуса, из которого
получен усеченный конус, АА1-одна из
образующих
Усеченного конуса О и О1 – центры
оснований. Используя формулу Sбок для
конуса получаем
S бок = πr*PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, отсюда,
учитывая, что AA1=L, находим
Sбок =πrL +π (r — r1)PA1
Выразим РА1 через L1, r и r1. Прямоугольные
треугольники РО1А1 и РОА подобны, так
как имеют общий острый угол Р и поэтому
PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаем
PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)
Sбок =πL(r+r1)
2. Площадь полной поверхности
усеченного конуса равна сумме площадей
боковой поверхности усеченного конуса
и оснований
Sполн
= S1+S2+Sбок=πL(r+r1)+
πR²+πr²
Обьем усеченного конуса
Объем усеченного конуса равен разности
объемов полного конуса и конуса,
отсекаемого плоскостью, параллельной
основанию конуса.. Обьем усеченного
конуса V, высота которого равна h, а
площади оснований S и S1 вычисляется по
формуле
V=1/3h(S+S1+√S*S1)
рисунок 8
рисунок 9
Касательной плоскостью
к конусу называется плоскость,
проходящая через образующую конуса
и перпендикулярная плоскости
осевого сечения, содержащей
эту образующую
За величину боковой поверхности конуса
(полного или усеченного) принимается
предел, к которому стремится боковая
поверхность вписанной в этот конус
правильной пирамиды (полной или
усеченной), когда число сторон правильного
многоугольника, вписанного в основание,
неограниченно увеличивается (и,
следовательно, площадь каждой боковой
грани неограниченно убывает).
Теорема. Боковая поверхность конуса
равна произведению длины окружности
основания на половину образующей.
В
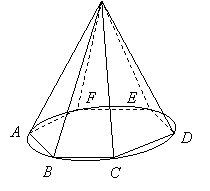
пишем
в конус какую-нибудь правильную пирамиду.
Пусть p — длина периметра
основания, l — длина
апофемы пирамиды, L —
образующая конуса. Предположим, что
число сторон вписанного в основание
многоугольника неограниченно возрастает.
Тогда периметр p будет
стремиться к пределу, принимаемому за
длину окружности основания C,
а апофема l будет иметь
пределом образующую конуса, значит
боковая поверхность вписанной пирамиды,
равная
,
будет стремиться к пределу
.
Этот предел и принимается за величину
боковой поверхности конуса, то есть
.
Чтобы получить полную поверхность
конуса, достаточно приложить к боковой
поверхности площадь основания:
.
Теоремы:.
Теорема. Плоскость, параллельная
плоскости основания конуса, пересекает
конус по кругу, а боковую поверхность
— по окружности с центром на оси
конуса.
Доказательство.
Пусть
— плоскость, параллельная плоскости
основания конуса и пересекающая конус
(рис.5). Преобразование гомотетии
относительно вершины конуса, совмещающее
плоскость
с плоскостью основания, совмещает
сечение конуса плоскостью
с основанием конуса. Следовательно,
сечение конуса плоскостью есть круг, а
сечение боковой поверхности – окружность
с центром на оси конуса. Теорема
доказана.
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Теоремы:
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Боковая
поверхность усеченного конуса равна
произведению полусуммы длин окружностей
оснований на образующую.
Доказательство.
В
пишем
в усеченный конус какую-нибудь правильную
усеченную пирамиду. Пусть p
— периметр нижнего основания,
—
периметр верхнего, l
— длина апофемы пирамиды,
L — образующая усеченного
конуса. При неограниченном возрастании
числа боковых граней вписанной пирамиды
периметры p и
стремятся
к пределам, принимаемым за длины
окружностей оснований C
и
,
а апофема l имеет
пределом образующую L
=> величина боковой поверхности
вписанной пирамиды, равная
,
будет стремиться к пределу
.
Этот предел и принимается за величину
боковой поверхности усеченного конуса,
то есть
.
Чтобы получить полную поверхность
усеченного конуса, достаточно приложить
к боковой поверхности сумму площадей
двух оснований:
.
Следствие:
Если в трапеции
,
от вращения которой получается конус,
провести среднюю линию BC,
то
=>
=>
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.
-
Формулы вычисления площади усеченного конуса
- 1. Боковая поверхность
- 2. Основания
- 3. Полная площадь
- Пример задачи
Формулы вычисления площади усеченного конуса
Примечание: иногда усеченный конус, также, называют коническим слоем.
1. Боковая поверхность
Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.
Sбок. = πRl + πrl = πl(R + r)
Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.
2. Основания
Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:
Sосн.1 = πR 2
Sосн.2 = πr 2
Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.
3. Полная площадь
Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.
Sполн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2)
Пример задачи
Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.
Решение
Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.
Sбок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см2
Sосн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см2
Sосн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см2
Sполн. = 427,04 см2 + 379,94 см2 + 113,04 см2 = 920,02 см2
Площадь поверхности усеченного конуса, формула.
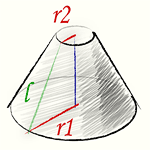 |
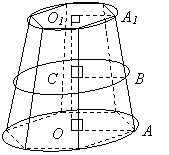
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом. |
Боковая площадь поверхности усеченного конуса, формула.
Боковая площадь поверхности усеченного конуса вычисляется по формуле:
[S=pi (r_1 + r_2) l]
(r1 — радиус нижнего основания усеченного конуса; r2 — радиус верхнего основания усеченного конуса; l — образующая усеченного конуса)
Вычислить площадь боковой поверхности усеченного конуса по формуле (1).
Полная площадь поверхности усеченного конуса, формула.
Полная площадь поверхности усеченного конуса равна сумме площадей боковой поверхности усеченного конуса и его оснований. Основания усеченного конуса есть круги и их площадь вычисляется по формуле площади круга:
[S=pi (r_1^2 + (r_1 + r_2) l + r_2^2) ]
(r — радиус вращения усеченного конуса; l — образующая усеченного конуса)
Вычислить площадь полной поверхности усеченного конуса по формуле (2).
Ссылки по теме
Площадь поверхности усеченного конуса |
стр. 314 |
|---|
ВИДЕОУРОК
Рассмотрим произвольный
конус и проведем плоскость, параллельную основанию конуса. Эта плоскость пересекает
конус по кругу и разбивает конус на две части. Одна из этих частей будет
конусом, а другую называют усечённым конусом.
Усечённым конусом
называется часть конуса, которая лежит между его основанием и секущей плоскостью,
параллельной основанию.
Основаниями усечённого
конуса называются основание
полного конуса, из которого получен усечённый, и часть секущей плоскости, ограниченная
конической поверхностью (круг).
Образующей усечённого
конуса называется
часть образующей полного конуса, заключённая между основаниями усечённого
конуса.
Высотой усечённого
конуса называется расстояние
между его основаниями.
Сечение усечённого
конуса плоскостью, которая проходит через его ось, называют осевым сечением усечённого
конуса.
Осевое сечение усечённого
конуса – равнобедренная трапеция, основания которой – диаметры оснований
конуса, боковые стороны – образующие усечённого конуса, высота этой трапеции равна
высоте усечённого конуса.
Боковая и полная поверхность усечённого
конуса.
В качестве величины
боковой поверхности усечённого конуса принимается граница, к которому стремится
величина боковой поверхности правильной вписанной (или описанной) в него
усечённой пирамиды при неограниченном увеличении числа её боковых граней.
Боковая поверхность
усечённого конуса равна произведению суммы длин окружностей оснований на
половину образующей.
Sбок =
πL(R + r),
где R и r – радиусы оснований усечённого конуса, а L – длина
образующей.
Чтобы найти площадь
полной поверхности усечённого конуса необходимо к площади его боковой поверхности
прибавить площади двух его оснований.
Полная поверхность
усечённого конуса равна сумме боковой поверхности и площадей оснований.
Sполн =
πL(R + r) + πR2 + πr2.
Боковая поверхность усечённого
конуса равна произведению высоты тела на длину окружности, радиус которого будет
перпендикуляр, опущенный с середины образующей на высоту тела.
Боковая поверхность усечённого конуса равна
Sбок = 2π × ОА × О1О2.
Развёртка усечённого конуса.
Если поверхность усечённого
конуса разрезать по образующей и окружностям оснований и развернуть так, чтобы
боковая поверхность с основаниями лежали в одной плоскости, то на плоскости получим
фигуру, называемую развёрткой усечённого конуса.
ЗАДАЧА:
Найдите боковую поверхность усечённого конуса, если его образующая
наклонена к плоскости основания под углом
60°,
а площадь осевого сечения равна S.
РЕШЕНИЕ:
Пусть дан усечённый конус
СА с площадью осевого
сечения
S и ∠ ABO
= 60°.
Найти боковую поверхность Sx усечённого конуса.
В равнобедренной трапеции
ВАDС из вершины А на основание
СВ опустим АМ ⊥
СВ. Обозначим
АВ
= L, ОВ = R, О1А
= r.
В прямоугольном ∆ АМВ из условия
∠ МАВ
= 30°, поэтому
По условию задачи площадь осевого сечения
(R + r)H = S,
или
Умножив обе две части равенства на число π, получим
Учитывая, что боковая поверхность усечённого конуса
Sx = πL(R + r),
находим
ОТВЕТ:
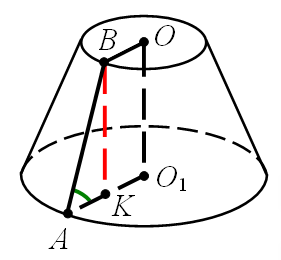
ЗАДАЧА:
Образующая усечённого конуса равна 2а и наклонена к основанию под углом 60°. Радиус одного основания в два раза больше радиуса
второго основания. Найдите каждый из радиусов.
РЕШЕНИЕ:
Пусть образующая усечённого конуса АВ = 2а,
а угол наклона образующей к плоскости основания конуса ∠ ВАО1 = 60°.
Учитывая, что
АО1 =
2ВО,
опустим из точки В на плоскость нижнего основания перпендикуляр
ВК ⊥ АО1 тогда
ВО = КО1 = АК.
З ∆ АВК АК = АВ cos∠ ВАК
АК = 2а cos
60° = а.
Тогда
АК = КО1 = ВО = а,
АО1 = 2а.
ОТВЕТ: а, 2а.
Задания к уроку 14
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Прямые и плоскости в пространстве
- Урок 2. Прямая призма
- Урок 3. Наклонная призма
- Урок 4. Правильная призма
- Урок 5. Параллелепипед
- Урок 6. Прямругольный параллелепипед
- Урок 7. Куб
- Урок 8. Пирамида
- Урок 9. Правильная пирамида
- Урок 10. Усечённая пирамида
- Урок 11. Цилиндр
- Урок 12. Вписанная и описанная призмы
- Урок 13. Конус
- Урок 15. Вписанная и описанная пирамиды
- Урок 16. Сфера и шар
- Урок 17. Комбинация тел