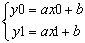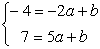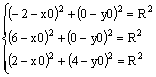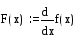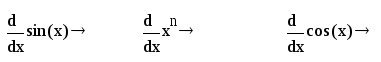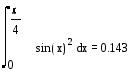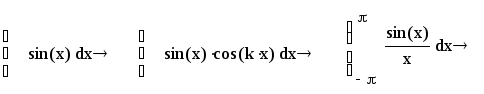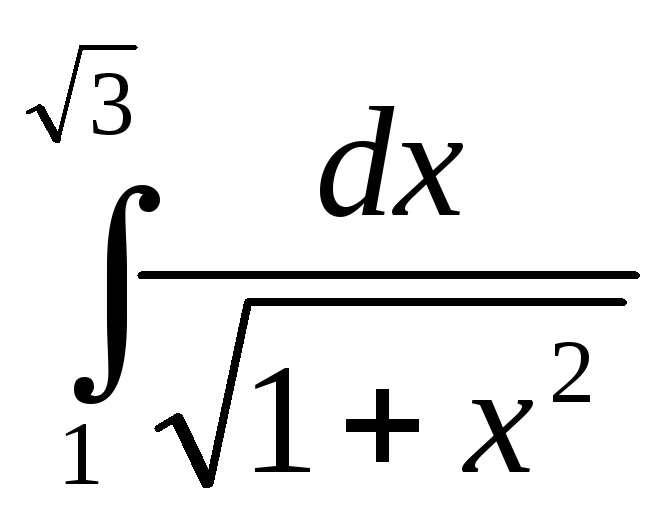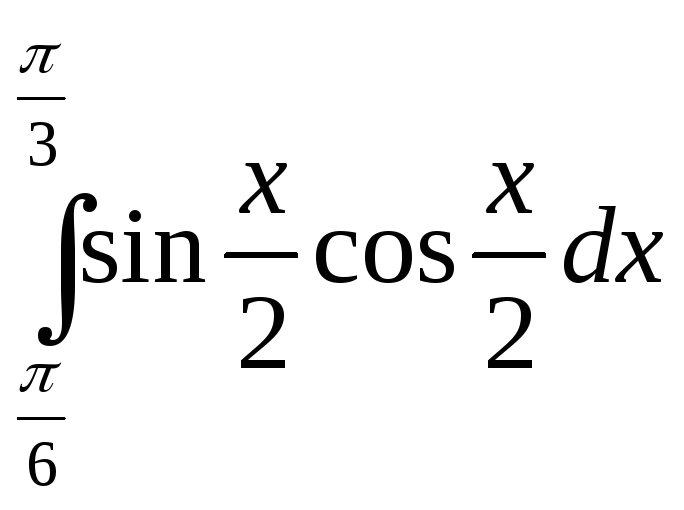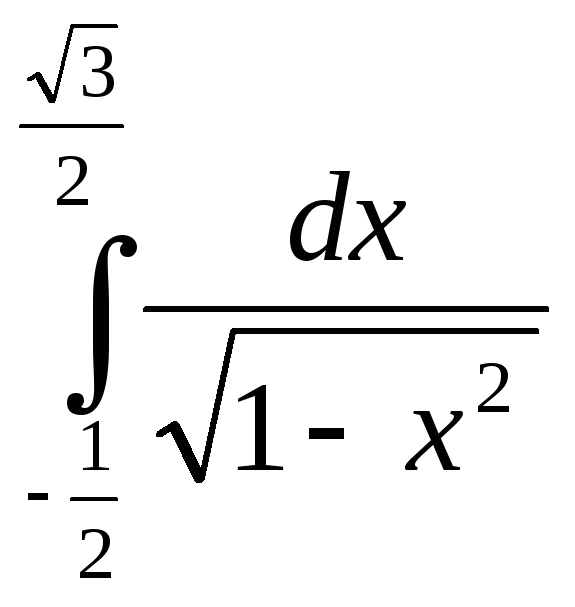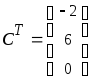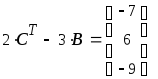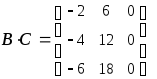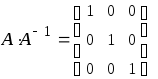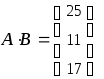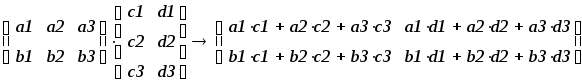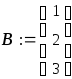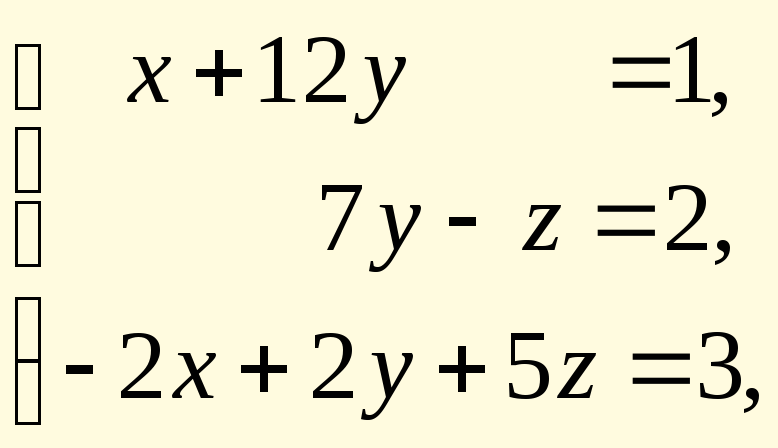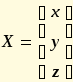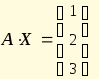|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
1 |
|
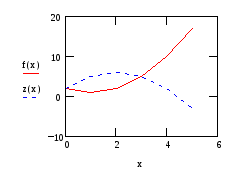
Площадь под графиком построенным по точкам27.11.2016, 05:39. Показов 12101. Ответов 14
Возможно ли как-то посчитать площадь под таким графиком, построенным по точкам Миниатюры
0 |
|
Модератор 1575 / 1444 / 468 Регистрация: 13.09.2015 Сообщений: 4,964 |
|
|
27.11.2016, 06:37 |
2 |
|
looee, можно, как сумму площадей трапеций.
0 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
27.11.2016, 07:07 |
3 |
|
посчитать площадь под таким графиком Можно также использовать интерполяцию и обычный интеграл.
1 |
|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
27.11.2016, 07:20 [ТС] |
4 |
|
А как это сделать? У нас же не задана зависимость F(ΔL) Миниатюры
0 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
27.11.2016, 08:06 |
5 |
|
правильно сделал? Все правильно
1 |
|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
30.11.2016, 13:49 [ТС] |
6 |
|
Centurio, А как посчитать площадь как сумму трапеций? Почему у меня не получается, в чем ошибка? Миниатюры
0 |
|
8732 / 6326 / 3402 Регистрация: 14.01.2014 Сообщений: 14,540 |
|
|
30.11.2016, 13:56 |
7 |
|
Загрузите Ваш Mathcad-файл в архиве, по фото всегда трудно сделать диагноз.
0 |
|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
30.11.2016, 14:53 [ТС] |
8 |
|
mathidiot, вот
0 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
30.11.2016, 15:03 |
9 |
|
площадь как сумму трапеций? 1. В случае табличного задания функции основаниями трапеций являются отрезки между соседними значениями аргументов, а верхние основания — отрезки между значениями функции в узловых точках.
1 |
|
8732 / 6326 / 3402 Регистрация: 14.01.2014 Сообщений: 14,540 |
|
|
30.11.2016, 15:16 |
10 |
|
Если я правильно понял, Вам надо было проинтегрировать от a=0,4 до b=191. Внизу вариант с исправлением ошибок, уже указанных Symon. Примечание: a и b можно было убрать из списка аргументов функции интегрирования, которое носит грубый характер из-за неравноотстоящих точек Миниатюры
1 |
|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
30.11.2016, 15:56 [ТС] |
11 |
|
mathidiot, Вопрос на картинке Миниатюры
0 |
|
8732 / 6326 / 3402 Регистрация: 14.01.2014 Сообщений: 14,540 |
|
|
30.11.2016, 18:55 |
12 |
|
Во-первых, этот вопрос надо было адресовать Вам, так как Вы его выбрали сами: h=(b-a)/n (я не стал менять, потому что надо было избавиться от ошибки вызова функции tr, когда Mathcad сообщал, что выражение должно быть целым числом).
1 |
|
Модератор 1575 / 1444 / 468 Регистрация: 13.09.2015 Сообщений: 4,964 |
|
|
30.11.2016, 18:57 |
13 |
|
А как посчитать площадь как сумму трапеций? Здесь получаются прямоугольные трапеции, как бы стоящие «на боку». Тогда длины оснований у каждой трапеции равны соседним значениям функции, а высоты равны прямым боковым сторонам, т.е. разностям между соседними значениями аргумента. Миниатюры
1 |
|
1 / 1 / 0 Регистрация: 13.11.2016 Сообщений: 39 |
|
|
30.11.2016, 19:14 [ТС] |
14 |
|
Centurio, Добавлено через 8 минут
1 |
|
Модератор 1575 / 1444 / 468 Регистрация: 13.09.2015 Сообщений: 4,964 |
|
|
30.11.2016, 19:20 |
15 |
|
Centurio, Так можно было? Конечно. Тем более график, построенный по точкам — это отрезки между соседними значениями функции, т.е. представляют из себя именно боковые стороны трапеций.
А зачем тогда нужен способ, который я пытался воплотить выше? Ну, не знаю. Зато в чём-то потренировались и что-то новое узнали.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
30.11.2016, 19:20 |
|
Помогаю со студенческими работами здесь
Площадь фигуры под графиком Закрасить площадь под графиком
помогите пожалуйста с графиком! не могу найти ошибку!!необходимо чтоб кривая проходила по точкам! interface uses Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 15 |
Презентация на тему: Интегральное исчисление. Нахождение площадей фигур в среде Mathcad
Интегральное исчисление.Нахождение площадей фигур в среде Mathcad Преподаватель математики: Шутилина С.Н.
Площадь фигуры Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых
Работа в Mathcad В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus
Формулировка задания Найти площадь фигуры, ограниченной кривыми:
Реализация в среде Mathcad Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)
Реализация в среде Mathcad Зададим обе функции:
Реализация в среде Mathcad Построим графики этих функций:
Реализация в среде Mathcad По графику определилась фигура, площадь которой нужно найти: Зададим эту новую функцию в Mathcad
Реализация в среде Mathcad Также графически определились приближенные пределы интегрирования Зададим приближенное значение нижнего предела интегрирования:
Реализация в среде Mathcad Точное значение нижнего предела интегрирования найдем с помощью функции root. Будем учитывать, что вместо f(x), в функции root используется g(x):
Реализация в среде Mathcad Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:
Реализация в среде Mathcad Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):
Выводы Среда Mathcad упрощает решение сложных математических задач и позволяет использовать на занятиях по математике не только традиционные методы, но и компьютерную технику, которая облегчает вычисления. Однако, существенным недостатком решения задач с помощью Mathcad является то, что среда выводит только конечный результат, поэтому промежуточные вычисления не видны пользователю
Интегральное исчисление. Нахождение площадей фигур в среде Mathcad
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Интегральное исчисление.
Нахождение площадей фигур в среде Mathcad
Преподаватель математики: Шутилина С.Н.
Площадь фигуры
Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых
Работа в Mathcad
В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus
Формулировка задания
Найти площадь фигуры, ограниченной кривыми:
Реализация в среде Mathcad
Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования
Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)
Реализация в среде Mathcad
Зададим обе функции:
Реализация в среде Mathcad
Построим графики этих функций:
Реализация в среде Mathcad
По графику определилась фигура, площадь которой нужно найти:
Зададим эту новую функцию в Mathcad
Реализация в среде Mathcad
Также графически определились приближенные пределы интегрирования
Зададим приближенное значение нижнего предела интегрирования:
Реализация в среде Mathcad
Точное значение нижнего предела интегрирования найдем с помощью функции root.
Будем учитывать, что вместо f(x), в функции root используется g(x):
Реализация в среде Mathcad
Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:
Реализация в среде Mathcad
Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):
Выводы
Среда Mathcad упрощает решение сложных математических задач и позволяет использовать на занятиях по математике не только традиционные методы, но и компьютерную технику, которая облегчает вычисления.
Однако, существенным недостатком решения задач с помощью Mathcad является то, что среда выводит только конечный результат, поэтому промежуточные вычисления не видны пользователю
Курс повышения квалификации
Охрана труда
- Сейчас обучается 100 человек из 43 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 351 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 217 человек из 54 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 540 407 материалов в базе
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 31.12.2020
- 4220
- 3
- 31.12.2020
- 4223
- 0
- 10.12.2020
- 4337
- 0
- 08.12.2020
- 4282
- 0
- 05.12.2020
- 4080
- 0
- 18.10.2020
- 4108
- 0
- 04.08.2020
- 4649
- 0
- 26.07.2020
- 3766
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 13.02.2020 181
- PPTX 1.6 мбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Цветкова Анна Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 23785
- Всего материалов: 237
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В России классы будут переводить на дистант, если заболели 20% детей
Время чтения: 1 минута
Новые курсы: школьные службы примирения, детская журналистика и другие
Время чтения: 15 минут
Онлайн-семинар о развитии управляющих функций мозга ребенка
Время чтения: 1 минута
Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Определение площадей фигур, ограниченных непрерывными линиями
8.2 Определение площадей фигур, ограниченных непрерывными линиями
Площадь криволинейной трапеции, ограниченной графиком функции f(x), отрезком [a,b] на оси Ox и двумя вертикалями х = а и х = b, a 2 и y = 0.
Рис. 6.5. Нахождение площади фигуры, ограниченной линиями f(x) = 1 – x 2 и y = 0
Площадь фигуры, заключенной между графиками функций f1(x) и f2(x)и прямыми х = а и х = b, вычисляется по формуле:
Внимание. Чтобы избежать ошибок при вычислении площади, разность функций надо брать по модулю. Таким образом, площадь будет всегда положительной величиной.
Пример. Нахождение площади фигуры, ограниченной линиями 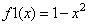
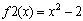
1. Строим график функций.
2. Находим точки пересечения функций с помощью функции root. Начальные приближения определим по графику.
3. Найденные значения x подставляем в формулу 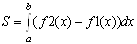
8.3 Построение кривых по заданным точкам
Построение прямой, проходящей через две заданные точки
Для составления уравнения прямой, проходящей через две точки А(x0,y0) и B(x1,y1), предлагается следующий алгоритм:
1. Прямая задается уравнением y = ax + b,
где a и b — коэффициенты прямой, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
2. Данная система является линейной. В ней две неизвестные переменные: a и b. Систему можно решить матричным способом.
Пример. Построение прямой, проходящей через точки А(–2,–4) и В(5,7).
Подставим в уравнение прямой координаты данных точек и получим систему:
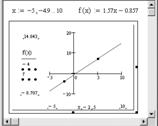
Решение этой системы в MathCAD представлено на рисунке 6.7.
Рис. 6.7.Решение системы
В результате решения системы получаем: а = 1.57, b = –0.857. Значит, уравнение прямой будет иметь вид: y = 1.57x – 0.857. Построим эту прямую (рис. 6.8).
Рис. 6.8. Построение прямой
Построение параболы, проходящей через три заданные точки
Для построения параболы, проходящей через три точки А(x0,y0), B(x1,y1) и C(x2,y2), алгоритм следующий:
1. Парабола задается уравнением
y = ax 2 + bх + с, где
а, b и с — коэффициенты параболы, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
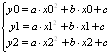
2. Данная система является линейной. В ней три неизвестные переменные: a, b и с. Систему можно решить матричным способом.
3. Полученные коэффициенты подставляем в уравнение и строим параболу.
Пример. Построение параболы, проходящей через точки А(–1,–4), B(1,–2) и C(3,16).
Подставляем в уравнение параболы заданные координаты точек и получаем систему:
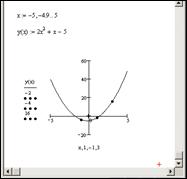
Решение этой системы уравнений в MathCAD представлено на рисунке 6.9.
Рис. 6.9. Решение системы уравнений
В результате получены коэффициенты: a = 2, b = 1, c = –5. Получаем уравнение параболы: 2x 2 +x –5 = y. Построим эту параболу (рис. 6.10).
Рис. 6.10. Построение параболы
Построение окружности, проходящей через три заданные точки
Для построения окружности, проходящей через три точки А(x1,y1), B(x2,y2) и C(x3,y3), можно воспользоваться следующим алгоритмом:
1. Окружность задается уравнением
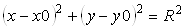
где x0,y0 — координаты центра окружности;
R — радиус окружности.
2. Подставим в уравнение окружности заданные координаты точек и получим систему:

Данная система является нелинейной. В ней три неизвестные переменные: x0, y0 и R. Система решается с применением вычислительного блока Given – Find.
Пример. Построение окружности, проходящей через три точки А(–2,0), B(6,0) и C(2,4).
Подставим в уравнение окружности заданные координаты точек и получим систему:
Решение системы в MathCAD представлено на рисунке 6.11.
Рис. 6.11. Решение системы
В результате решения системы получено: x0 = 2, y0 = 0, R = 4. Подставим полученные координаты центра окружности и радиус в уравнение окружности. Получим: 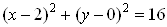
http://infourok.ru/integralnoe-ischislenie-nahozhdenie-ploshadej-figur-v-srede-mathcad-4865233.html
http://kazedu.com/referat/132524/4
-
Лилия92
- Сообщения: 3
- Зарегистрирован: Пн сен 27, 2010 2:13 pm
Площадь в MathCAD помогите
Как определить функцию которыя находит:
площадь квадрата
площадь окружности
площадь прямоугольного треугольника
площадь ромба
расстояние d м.д точками в R^3-пространстве
-
1_and_0
- Сообщения: 23
- Зарегистрирован: Чт май 14, 2009 11:55 pm
- Откуда: СПб
- Контактная информация:
Сообщение 1_and_0 » Ср сен 29, 2010 4:22 pm
пиши в аську 421881816, скажу да покажу как это сделать.
С уважением,
Мельников В.Ю.
-
VFO
- Сообщения: 4227
- Зарегистрирован: Ср фев 27, 2002 8:03 pm
Re: Площадь в MathCAD помогите
Сообщение VFO » Ср сен 29, 2010 7:55 pm
Лилия92 писал(а):Как определить функцию которыя находит:
площадь квадрата
площадь окружности
площадь прямоугольного треугольника
площадь ромба
расстояние d м.д точками в R^3-пространстве
площадь квадрата S(a):=a^2
площадь круга S(r):= pi*r^2 (колеса у поезда стучат из-за этого квадрата)
площадь прямоугольного треугольника S(a.b):=a*b/2
etc
Или я что-то недопонял.
Все эти формулы есть в шпаргадках Mathcad.
-
Лилия92
- Сообщения: 3
- Зарегистрирован: Пн сен 27, 2010 2:13 pm
Сообщение Лилия92 » Чт сен 30, 2010 5:42 pm
Спасибо большое=)
-
Лилия92
- Сообщения: 3
- Зарегистрирован: Пн сен 27, 2010 2:13 pm
Сообщение Лилия92 » Чт сен 30, 2010 5:43 pm
А последние два? как сделать их?
Понимаете,у нас такой препод,что ничего не объясняет,а требует…извините, если я спрашиваю элементарные вещи..
-
VFO
- Сообщения: 4227
- Зарегистрирован: Ср фев 27, 2002 8:03 pm
Сообщение VFO » Пт окт 01, 2010 8:42 pm
Лилия92 писал(а):А последние два? как сделать их?
Понимаете,у нас такой препод,что ничего не объясняет,а требует…извините, если я спрашиваю элементарные вещи..
Высшее образование — это в первую очередь самообразование!
10
ЛАБОРАТОРНАЯ
РАБОТА № 4
Дифференцирование
функции. Геометрический смысл производной.
Цель.
Научиться находить численное значение
производной функции в заданной точке.
Вычисление
производной функции.
Оператор
производной Mathcad
предназначен для нахождения численного
значения производной функции в заданной
точке. Для вычисления производной
используется клавиша со знаком ?.
Для
того, чтобы найти производную функции
и вычислить ее численное значение,
необходимо сделать следующее:
-
Сначала
определить точку, в которой необходимо
найти производную. -
Щелкнуть
ниже определения этой точки. Затем
набрать ?. Появится оператор производной
с двумя полями:
-
Щелкнуть
на поле в знаменателе и набрать имя
переменной, по которой проводится
дифференцирование. -
Щелкнуть
на поле справа от
и набрать выражение, которое нужно
дифференцировать. -
Чтобы
увидеть результат, нажать знак =.
Задание 1.1
Найти производную
по
в точке
Решение:
Определим точку,
в которой необходимо найти производную:
Введем оператор
производной, заполним поля и вычислим
производную:
*
Результат дифференцирования есть не
функция, а число – значение производной
в указанной точке переменной
дифференцирования.
Хотя
дифференцирование возвращает только
одно число, можно определить одну функцию
как производную другой функции. Например:
.
Вычисление
f(x)
будет возвращать в численной форме
производную g(x)
в точке х.
Выражение,
которое нужно дифференцировать, может
быть вещественным или комплексным.
Переменная
дифференцирования должна быть простой
неиндексированной переменной.
Геометрический
смысл производной.
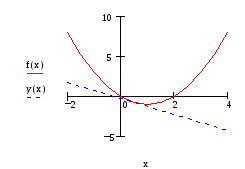
Задание 1.2.
Дана функция у=f(x). Построить график
функции и касательную к графику в точке
с абсциссой x=x0, если
—
уравнение касательной.
Введем данную
функцию и найдем ее значение в точке
:
Найдем значение
производной данной функции в точке
:
Запишем уравнение
касательной для данной функции:
Построим график
данной функции и касательную к ней.
Задания
3. Выполнить
дифференциальные вычисления в символьном
виде:
Задание
4.
Найти
производную функции в произвольной
точке.
-
5.
9.
-
6.
10.
-
7.
-
8.
Задание
5.
Дана
функция y=f(x).
Построить график функции и касательную
к графику в точке с абсциссой x=x0.
Y=f(x0)(x-x0)+f(x0)
– уравнение касательной.
1.
6.
,
x0=π∕6
-
,
x0=2
7.
,
x0=-1 -
,
x0=e 8.
,
x0=-π/2 -
,
x0=-1 9.
,
x0=3 -
,
x0=1 10.
,
x0=-2
Содержание
отчета:
-
Задания
1 и 2, 3, 4, 5.
ЛАБОРАТОРНАЯ
РАБОТА № 5.
Интегральное
исчисление.
Цель.
Научиться
находить определенные интегралы функций,
вычислять площадь фигуры при помощи
интеграла.
-
Определенный
интеграл.
Оператор
интегрирования в Mathcad
предназначен для численного вычисления
определенного интеграла функции по
некоторому интервалу.
Знак
интеграла выводится при нажатии клавиши
со знаком &.
Для
того, чтобы вычислить определенный
интеграл, необходимо сделать следующее:
-
Щелкнуть
в свободном месте и набрать знак &.
Появится знак интеграла с пустыми
полями для подынтегрального выражения,
пределов интегрирования и переменной
интегрирования: ∫ -
Щелкнуть
на поле внизу и набрать нижний предел
интегрирования. Щелкнуть на верхнем
поле и набрать верхний предел
интегрирования. -
Щелкнуть
на поле между знаком интеграла и d
и набрать выражение, которое нужно
интегрировать. -
Щелкнуть
на последнее пустое поле и набрать
переменную интегрирования. -
Чтобы
увидеть результат, нажать знак =.
Задание 1.1
Вычислить определенный
интеграл

от 0 до
Решение:
Введем знак
интеграла и заполним пустые поля;
вычислим интеграл:
*Пределы
интегрирования должны быть вещественными.
Выражение, которое нужно интегрировать
может быть вещественным, либо комплексным.
Кроме переменной интегрирования, все
переменные в подынтегральном выражении
должны быть определены ранее в другом
месте рабочего документа. Переменная
интегрирования должна быть простой
переменной без индекса. Если переменная
интегрирования является размерной
величиной, верхний и нижний пределы
интегрирования должны иметь ту же самую
размерность.
-
Площадь
фигуры. Как
известно, при помощи определенного
интеграла можно вычислять площадь
фигуры.
Задание
2.1. Найти площадь
фигуры, ограниченной графиками функций:
Решение.
Построим графики
этих функций в одном графическом блоке:
Вычислим площадь
полученной фигуры:
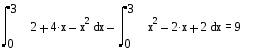
Задание 2.1.
Выполнить
интегральные вычисления в символьном
виде:
Задания 3.1
Вычислить
определенный интеграл.
-
2.
3.dx
4.
5.
6.
7.
7.
9.
10.
Задание
3.2.
Найти
площадь фигуры, ограниченной графиками
функций. Построить эту фигуру.
-
6.
-
7.
-
8. -
9. -
10.
Содержание
отчета: Задания
1 и 2, 3.
ЛАБОРАТОРНАЯ
РАБОТА № 6.
Матрицы
Цель.
Научиться
основным приемам работы с матрицами.
-
Основные
операции с матрицами
Очень часто в расчетах
необходимо использовать массивы чисел.
MathCAD поддерживает два вида массивов —
одномерные (векторы) и двумерные
(матрицы). Элементами массива могут быть
числа, строки, математические выражения
и даже другие массивы. Переменной может
быть присвоено значение матрицы
(вектор-столбец — это матрица с одним
столбцом). Основные операции для работы
с векторами и матрицами собраны на
панели математических инструментов
Matrix.
Простой
способ
ввести
матрицу —
комбинация
клавиш Ctrl+M.
|
Над |
||
|
вычислить матрицы A: |
|
Знак |
|
вычислить |
|
Минус Оператор |
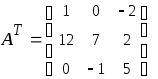
|
транспонировать
заменить ее наоборот): |
|
Кнопка Можно |
|
складывать |
|
Знак |
|
перемножать |
|
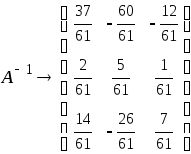
Задание 1.1. Найти
определитель матрицы, обратную и
транспонированную матрицы.
-
Решение системы
линейных уравнений называют
матричным
методом.
Систему линейных
уравнений
у которой
коэффициенты при неизвестных составляют
квадратную матрицу

а свободные члены составляют матрицу
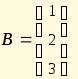
можно
записать в виде
матричного уравнения
, где
есть матрица-столбец неизвестных.
Столбец неизвестных находится из
матричного уравнения умножением его
частей слева на обратную матрицу
,
которая
существует, если только определитель
матрицы системы
отличен от нуля. В результате получим
(так как
, где
единичная матрица). Этот метод решения
системы линейных уравнений называют
матричным
методом. В
нашем случае получаем (численно и
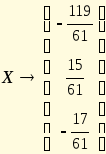
символьно):
Проверка решения заключается
в подстановке найденного решения в
матричное уравнение, которое при этом
должно обратиться в верное равенство.
В результате подстановки получаем:
Задание 3.
3.1. Найти
определитель матрицы, обратную и
транспонированную матрицы.
Матрицу 5х5 составляем
самостоятельно.
3.2.
Решить систему линейных уравнений
матричным методом.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



 Так можно было?
Так можно было?  А зачем тогда нужен способ, который я пытался воплотить выше?
А зачем тогда нужен способ, который я пытался воплотить выше? Площадь под графиком
Площадь под графиком