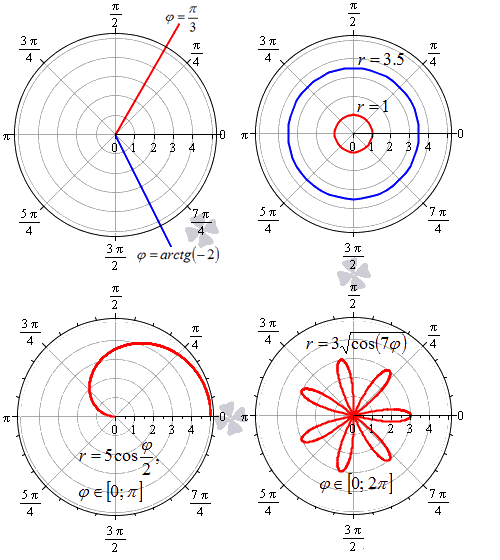
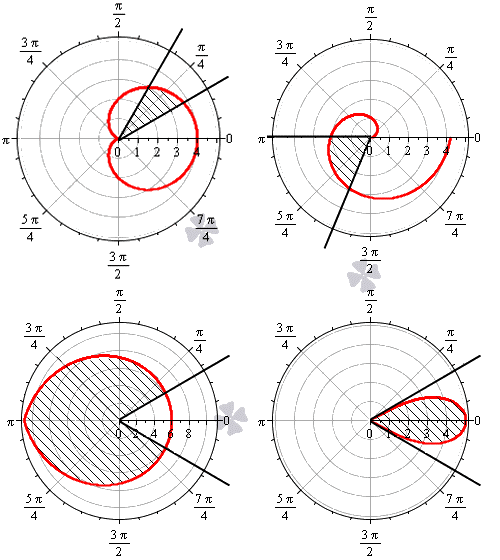
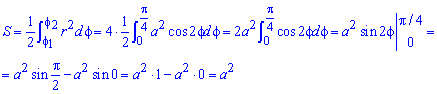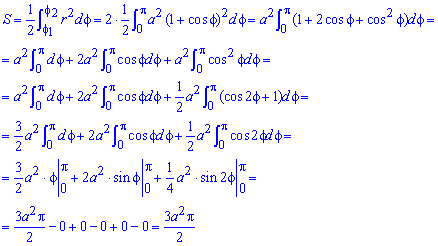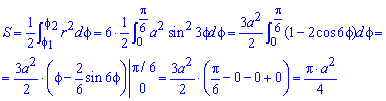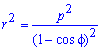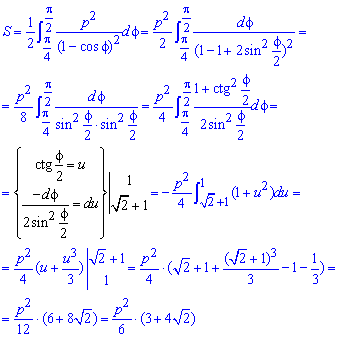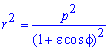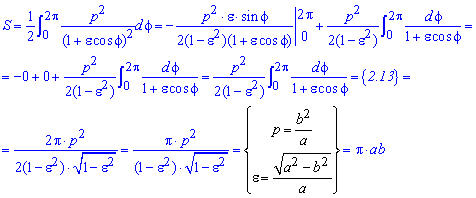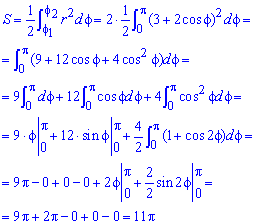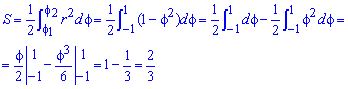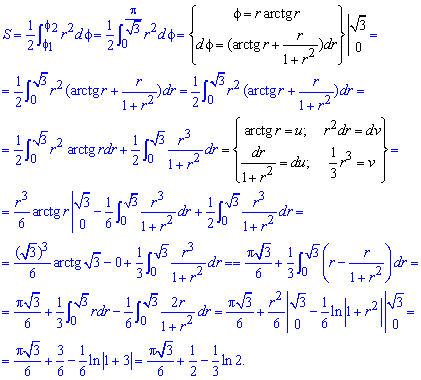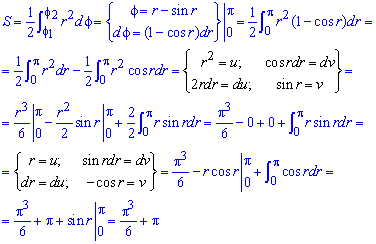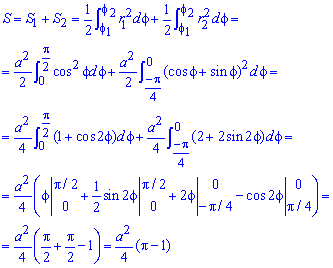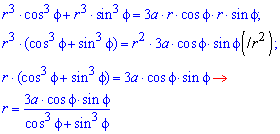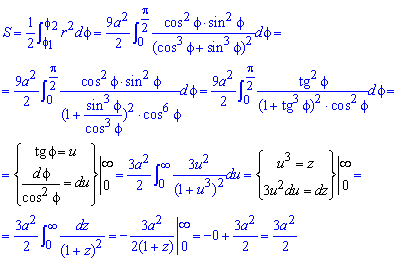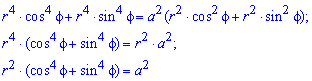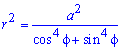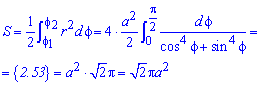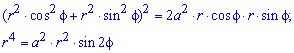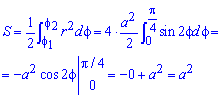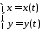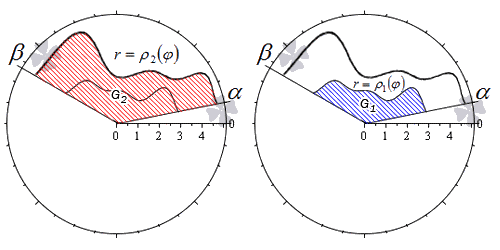Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
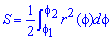
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
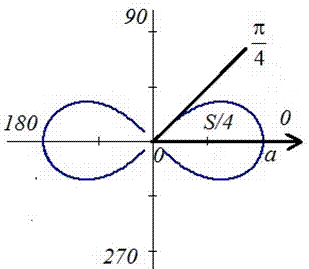
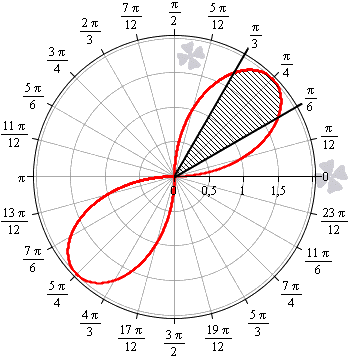
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли — геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
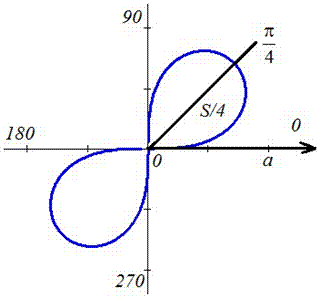
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
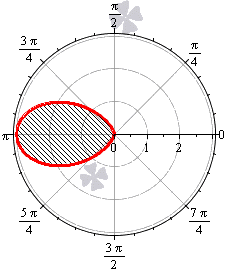
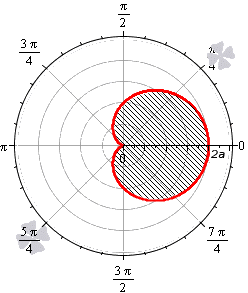
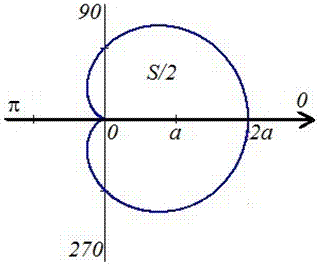
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) — кардиоида.
Вычисление: Кардиоида — плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
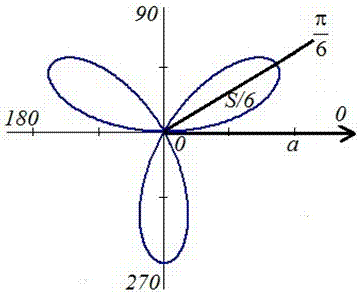
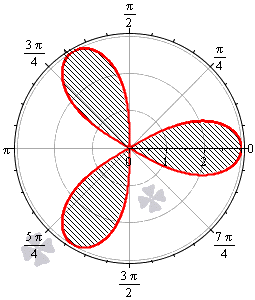
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
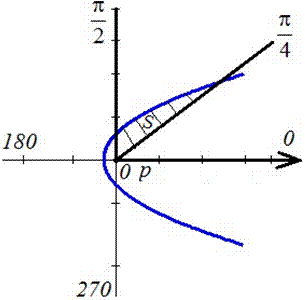
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 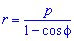
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 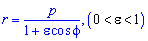
Вычисление: Запишем подинтегральную функцию:
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
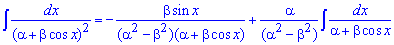
При выведении этой формулы пользовались методом интегрирования частями!
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
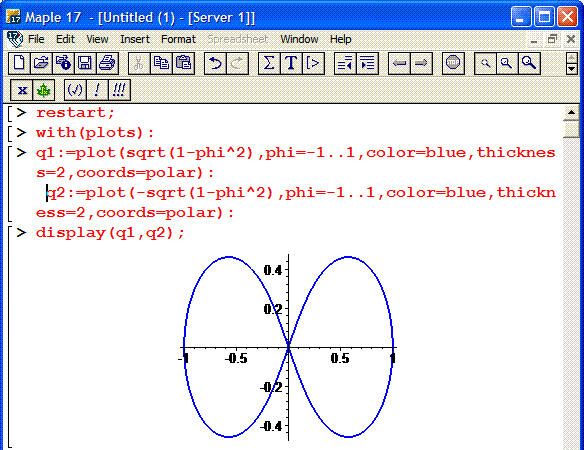
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
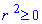
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми 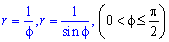
Вычисление: Выписываем подинтегральные функции:
Поскольку на промежутке интегрирования 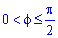
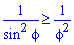
Найдем пределы интегрирования: f1=0 — особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
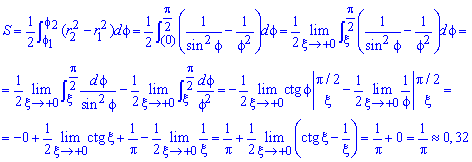
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой 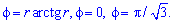
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
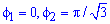
График функций имеет вид
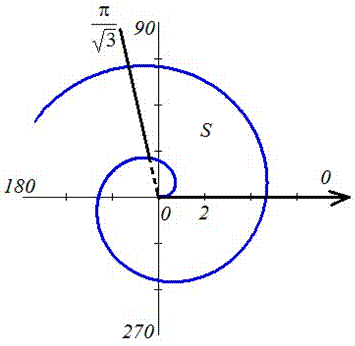
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
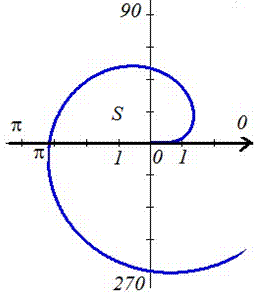
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
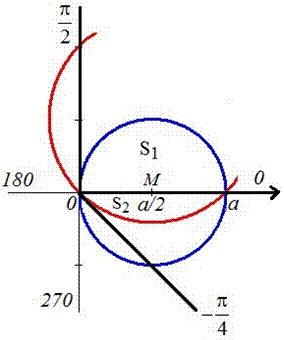
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
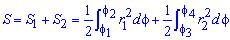
Записываем уравнение подинтегральных функций:
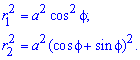
Определяем пределы интегрирования:
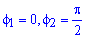
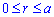
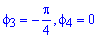
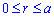
Вычисляем площадь изображенной фигуры интегрированием
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак «минус».
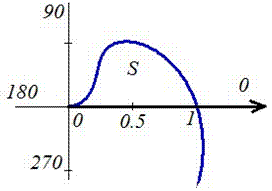
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
Перед интегралом (после замены переменных) поставили знак «минус», поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
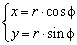
При подстановке в уравнение получим
Поднесем к квадрату, чтобы получить подинтегральную функцию:
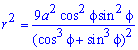
Выпишем пределы интегрирования:
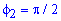
График функции имеет вид
Найдем площадь фигуры интегрированиям:
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
Выражаемый подинтегральную функцию делением:
Запишем пределы интегрирования:
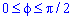
Ее график изображен на рисунку
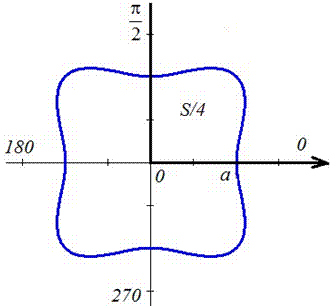
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
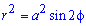
График исследуемой кривой следующий
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 
Находим площадь фигуры интегрированием:
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.
Онлайн калькулятор поможет вычислить площадь фигуры в полярных координатах, Вам пригодятся навыки построения графиков функций в полярной системе координат.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
Площадь
плоской фигуры, уравнение которой задано
в явном виде
Пусть
функция у = f(x) определена, непрерывна и
неотрицательна на отрезке [а; b], тогда
плоская фигура, ограниченная дугой
графика функции на этом отрезке и прямыми
х = а, х = b, у = 0, называется криволинейной
трапецией. Площадь
криволинейной трапеции определяется
по формуле:

Площадь
«сложной» фигуры
Под
«сложной» фигурой будем понимать часть
плоскости, ограниченную непрерывными
на отрезке [а; b] кривыми
у
= f(x) и у = g(x) (f(x)
g(x),
x[а;
b]) и прямыми х = а,
х
= b. Площадь «сложной» фигуры находится
по формуле:
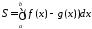
Распространенной
является постановка задачи о площади
плоской фигуры, ограниченной двумя
кривыми. Предполагается, что эти кривые,
пересекаясь, образуют некоторую
ограниченную фигуру. В этом случае
пределы интегрирования (х = а, х = b) заранее
не известны и должны быть определены
из решения системы уравнений:
Если
задача поставлена корректно, то эта
система имеет два решения, которые
определяют координаты точек пересечения
кривых.
Площадь
фигуры, ограниченной параметрически
заданной кривой
Пусть
— параметрическое уравнение кусочно-гладкой
простой замкнутой кривой, проходимой
против часовой стрелки. Тогда формула
площади ограниченной данной кривой
фигуры имеет вид:
Если
при изменении параметра t от 0 до Т кривая
проходит по часовой стрелке, то в этих
формулах необходимо сменить знак на
противоположный.
Площадь
плоской фигуры, уравнение которой задано
в полярных координатах
Площадь
сектора,
ограниченного непрерывной кривой
r
= r()
и лучами=
;
=
(
<
),
равна
Площадь
сегмента,
ограниченного непрерывными кривыми r
= r()
и р = р()
и лучами=
;
=
(
<
),
равна
11. Длина дуги кривой, уравнение которой задано в явном виде, параметрическими уравнениями, уравнениями в полярных координатах.
Равенство
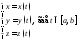
кривой, а переменнаяt– параметром. Точка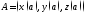

концом кривой. Аналогично определяется
плоская кривая с помощью равенств
Кривая
lназыв замкнутой,
если ее начало совподает с концома=в.
Криваяlназыв непрерывно
дифференцируемой, если функции


Рассмотрим
плоскую кривую lи
поставим вопрос о вычислении ее
длинны. Возьмем разбиение

Это разбиение имеет вид

Каждой точке

Соединив т.

вписана в кривуюl.
Каждому разбиению


длину этой ломанной
где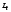
положительное число, которое соответствует
всякому разбиению
Кривая
lназывспрямляемой,
если

при этом сам придел
Th:
(вычисление длинны кривой (заданная
в явном виде)) Пустьlнепрерывно дифференцированная плоская
кривая, заданная уравнением
тогда криваяlспрямляема
и ее длина вычисляется по формуле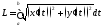
Док-во:
Возьмем

Пусть
длинная вписанная ломаная
тогда имеем
Применим формулу Лагранжа к функции
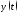
тогда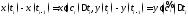
где

получим:
Правая часть (1) похожа на интегральную
сумму функции А, но ей не является, т.к.
Покажем, что сумма в формуле (1) стремится
при

т.е. к интегралу
(1), что кривая иlспрямляема и ее длина имеет вид
■.
Th:
Длина дуги заданной
явным уравнением

Док-во:
Дугу AB произвольным образом разделим
на n-частей, с точками:

Через точки

Интегральная
сумма для длины дуги.

■.
Вычисление
дуги AB заданной параметрически
Задача:
Найти длину дуги, если AB:
Имеет
место формула:
(2′)
Док-во:
Используем формулу (2)
Сокращая,
получаем формулу (2′). Вычисление длины
дуги AB заданной в полярной системе
координат. Выражение под знаком интеграла
в формуле (2) равно
и
называется дифференциалом длины дуги.
Используя
связь между ПСК и ДПСК, получаем:
(2»).
Соседние файлы в папке !!!!!
- #
- #
- #
Вычисление площади фигуры в полярных координатах
В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Полярная система координат и криволинейный сектор
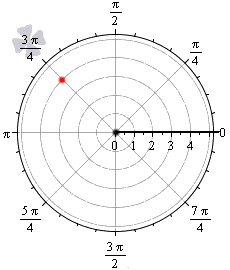
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .
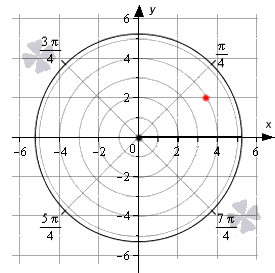
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .
Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.
Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
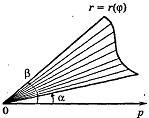
Дадим определение криволинейному сектору.
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .
На рисунке мы привели несколько примеров криволинейных секторов.
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.
Площадь криволинейного сектора — вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.
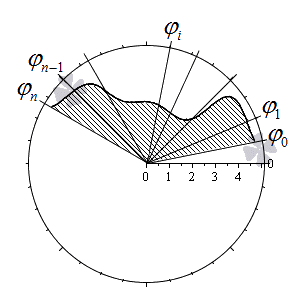
Разобьем криволинейный сектор на n частей такими лучами
φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:
S ( G ) = ∑ i = 1 n S ( G i )
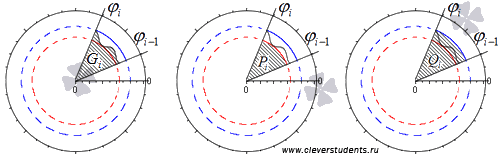
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.
Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.
Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .
Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ
Формула для определения площади криволинейного сектора имеет вид:
S ( G ) = 1 2 ∫ β α p 2 φ d φ
Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
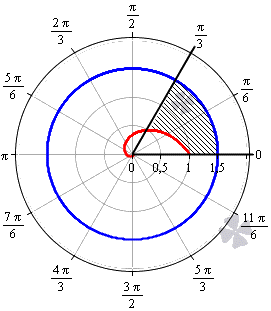
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4
Ответ: S ( G ) = π 6 + 3 4
Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :
— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z
Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .
S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .
∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .
Ответ: S ( G ) = 45 π 32
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z
Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.
Построим фигуру на графике.
Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):
1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
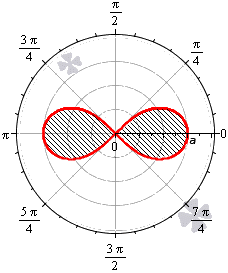
Площадь фигуры, которую ограничивает лемниската Бернулли
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.
Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :
S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2
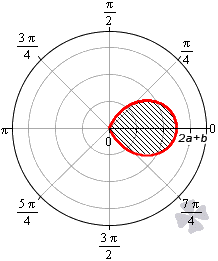
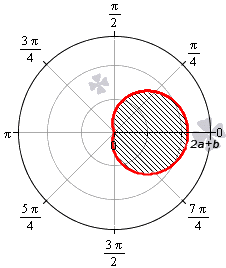
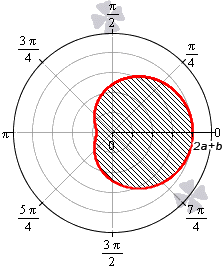
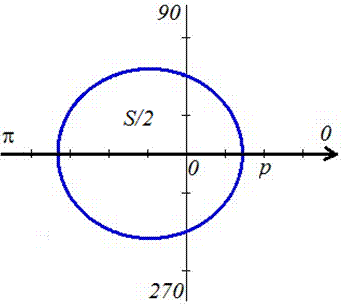
Площадь фигуры, которую ограничивает улитка Паскаля
В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .
При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .
При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.
Решение
Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..
Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:
— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3
Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:
S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π
Ответ: S ( G ) = 33 π
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
Исходя из этого, найдем площадь фигуры по формуле:
S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .
Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ
Последний переход возможен в силу третьего свойства определенного интеграла.
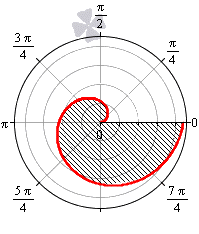
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.
Решение
Построим заданную фигуру на графике.
Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:
S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
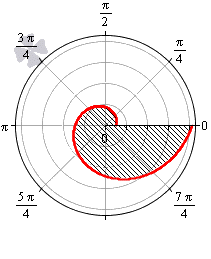
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ
Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:
S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6
Вычислить площадь фигуры заданной уравнением в полярных координатах онлайн
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Вычислить площадь фигуры, ограниченной кривыми онлайн
Вычисление площадей плоских фигур является одним из приложений определенного интеграла.
Для того, чтобы получить площадь фигуры изображенной на рисунке, необходимо вычислить определенный интеграл вида:
Функции и как правило, известны из условия задачи, а вот абсциссы их точек пересечения и придется дополнительно найти. Для этого необходимо решить уравнение:
Описанным выше способом, можно также найти площадь криволинейной трапеции в случае, если графики функций и не пересекаются, но точки и заданы по условию задачи:
В этом случае криволинейная трапеция (фигура площадь которой мы вычисляем) образована графиками функций , и прямыми , .
Онлайн калькулятор, построенный на основе системы Wolfram Alpha, автоматически вычислит площадь фигуры, образованной пересечением двух графиков функций.
http://yukhym.com/ru/integrirovanie-funktsii/ploshchad-figury-v-polyarnykh-koordinatakh.html
http://mathforyou.net/online/calculus/area/between/
Лекция 6 u Геометрические приложения определённого интеграла
Площадь плоской фигуры o 1. o Площадь плоской фигуры, граница которой задана в прямоугольных декартовых координатах: Если непрерывная кривая (кусочно-непрерывная) задана в прямоугольных декартовых координатах уравнением , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными линиями и осью Ох: определяется формулой: Пример 1: Вычислить площадь плоской фигуры, ограниченной параболой, прямыми х=1, х=3 и осью Ох: . Искомая площадь равна:
Примеры (декартовая С. К. ) o Пример 2: Вычислить площадь плоской фигуры, ограниченной кривой: и осью ординат. Здесь изменены роли функции и аргумента. Эффективнее рассматривать зависимость Тогда Рассмотрим случай произвольной непрерывной (кусочно-непрерывной) на отрезке. Пусть фигура ограничена теперь сверху и снизу функциями:
Геометрический смысл o В случае, если ограничивающие фигуру линии находятся в верхней части системы координат, то сдвигаем графики функций вверх на величину С: вверх и тогда получим:
Правильная область по определённому напрвлению o Площадь фигуры, изображённой на предыдущем рисунке может быть найдена по формуле: (*) Замечание: формула (*) вычисления площади плоской фигуры верна для правильных в направлении оси Oy областей. Область D называется правильной в направлении оси Oy, если выполнено: т. е. отрезок, соединяющих любые две точки области также ей принадлежит.
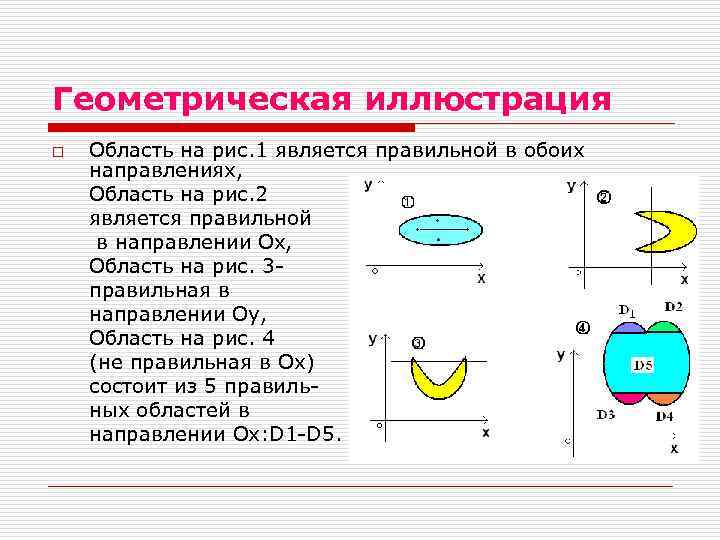
Геометрическая иллюстрация o Область на рис. 1 является правильной в обоих направлениях, Область на рис. 2 является правильной в направлении Ox, Область на рис. 3 правильная в направлении Оy, Область на рис. 4 (не правильная в Ох) состоит из 5 правильных областей в направлении Ox: D 1 -D 5.
Площадь фигуры, ограниченной линиями, заданных в параметрической форме o Пусть границы области заданы уравнениями: Площадь криволинейной трапеции, ограниченной этой линией, прямыми , осью Ox, есть: Пример 3: Вычислить площадь фигуры, ограниченной эллипсом:
Пример 3 o Ввиду симметрии фигуры, достаточно вычислить площадь четвёртой части её: заметим, что: Тогда:
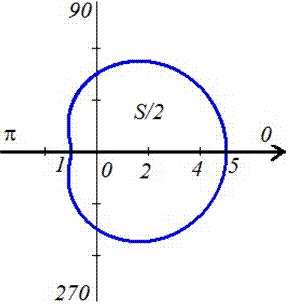
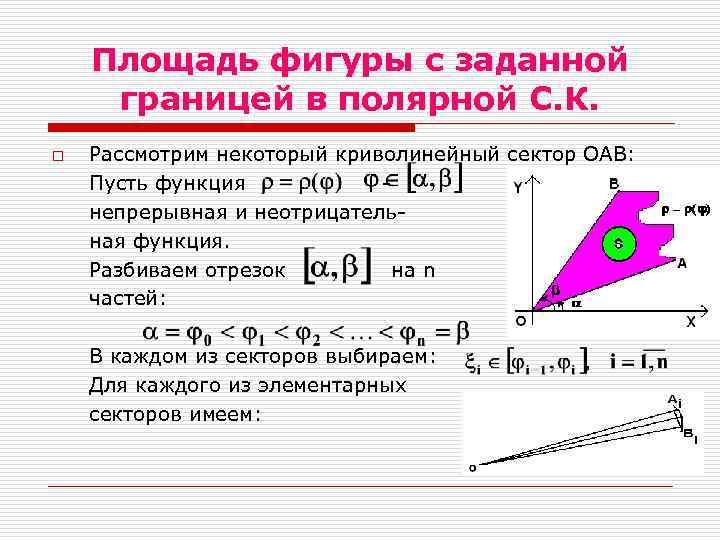
Площадь фигуры с заданной границей в полярной С. К. o Рассмотрим некоторый криволинейный сектор ОАВ: Пусть функция непрерывная и неотрицательная функция. Разбиваем отрезок на n частей: В каждом из секторов выбираем: Для каждого из элементарных секторов имеем:
Вывод формулы площади в ПСК o Тогда имеем: тогда получим интегральную сумму, предел которой равен: Пример 4: Найти площадь фигуры, заключённой внутри лемнискаты Бернулли: В силу симметрии фигуры, имеем:
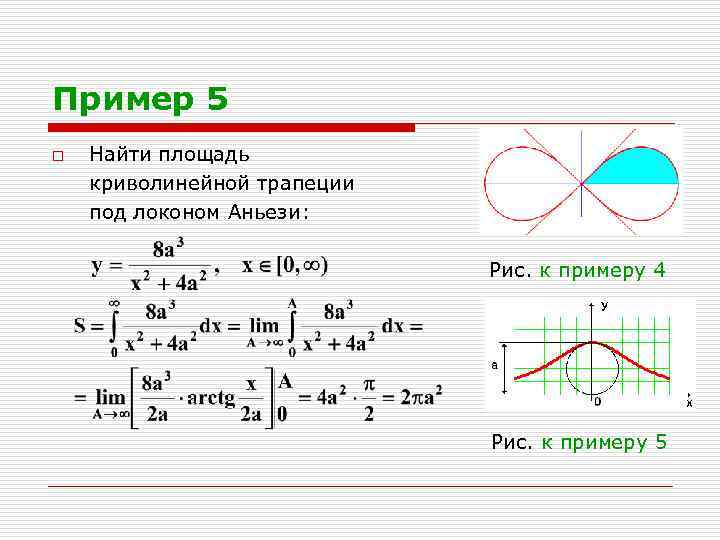
Пример 5 o Найти площадь криволинейной трапеции под локоном Аньези: Рис. к примеру 4 Рис. к примеру 5
Длина дуги плоской линии o o Пусть плоская линия L задана уравнением в ДСК: где , т. е. гладкая линия без изломов. Рассмотрим разбиение отрезка на n частей (произвольной длины): Проведём хорды, соединяя последовательно точки разбиения отрезка, длины которых равны, соответственно: Т. о. получим ломаную линию, вписанную в дугу, для которой имеем: Длиной дуги называется предел, к которому стремится длина вписанной ломаной линии при стремлении частичных отрезков длин к нулю и
Длина дуги плоской линии o Указанное выше определение в аналитическом виде: (*) Теорема 1: Если функция непрерывна со своей производной на отрезке задания, то такой предел (*)существует и длина дуги линии, заданной зависимостью выражается формулой: доказательство: Обозначим:
Доказательство Т 1 o Рассмотрим: , где -согласно теореме Лагранжа. Тогда имеем: и переходя к пределу, получим: (т. к. — непрерывная функция, то ) и тогда:
Пример 1: o Рассмотрим окружность с центром в начале координат. Тогда верхняя часть её (полуокружность) описывается функцией: — непрерывная функция Поэтому, формулу для вычисления длины дуги законно применить только на отрезке: на котором функция непрерывна вместе с производной :
Длина дуги линии, заданной уравнением в параметрической форме Далее получим: т. е. длина полуокружности равна. Пусть функция задана уравнением в параметрической форме: , где — -гладкие функции и тогда имеем:
Пример 2 o Найти длину одной арки циклоиды: Для этого найдём производные: Тогда длина дуги вычисляется по формуле:
Длина дуги линии, заданной уравнением в полярной СК o Пусть линия задана уравнением: Тогда, после преобразований: получим:
Пример 3 o Найти длину линии, заданной уравнением: Т. к. то т. о. И
Объём тела вращения o Пусть Г – есть кривая, описываемая в ДСК x. Oy непрерывной положительной функцией Для вычисления элементарного объёма тела вращения линии Г вокруг оси Ох произведём разбиение отрезка на n частей: и тогда элементарный объём тела, ограниченного плоскостями вычисляется по формуле:
Формула для вычисления объёма тела вращения o После чего, переходим к пределу и получаем формулу для определения объёма тела вращения вокруг оси Ох: т. е. Если вращение кривой происходит вокруг другой оси координат, например Oy, тогда объём вычисляется по формуле:
Пример 4 (ТР № 15) o Вычислить объём тела вращения фигуры, заданной уравнением: вокруг оси Оy. Тогда имеем:
Площадь поверхности тела вращения o Пусть функция вместе со своей производной элементарная площадь поверхности тела вращения вокруг оси Ох равна: — непрерывная. Тогда: Если вращение производится вокруг оси Oy, то соответствующая площадь определяется по формуле:
Пример 5: Вычислить площадь поверхности тора: вращение вокруг оси Ох. Находим: и o