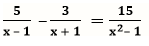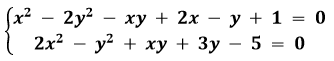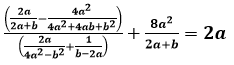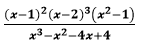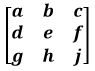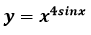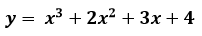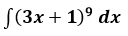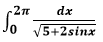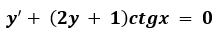EMBED
Make your selections below, then copy and paste the code below into your HTML source.
* For personal use only.
Theme
Output Type
Lightbox
Popup
Inline
Widget controls displayed
Widget results displayed
To add the widget to Blogger, click here and follow the easy directions provided by Blogger.
To add the widget to iGoogle, click here. On the next page click the «Add» button. You will then see the widget on your iGoogle account.
To embed this widget in a post on your WordPress blog, copy and paste the shortcode below into the HTML source:
For self-hosted WordPress blogs
To add a widget to a MediaWiki site, the wiki must have the Widgets Extension installed, as well as the code for the Wolfram|Alpha widget.
To include the widget in a wiki page, paste the code below into the page source.
Время на прочтение
4 мин
Количество просмотров 13K
Перевод поста Peter Barendse «Surfaces and Solids of Revolution: Using Wolfram|Alpha’s «Virtual Potter’s Wheel»».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации
Ещё до появления современной технологии 3D печати у нас была возможность создавать объекты практически любой формы, и единственные ограничения для человечества были связаны лишь с точностью, которую мы можем обеспечить. И на пути преодоления этих ограничений были разработаны разнообразные устройства, способные производить изделия очень сложных форм; кульминацией этого процесса (до появления 3D-принтеров) стало появление станков с ЧПУ и большим количеством степеней свободы:
Исторически одним из первых подобных устройств, был, пожалуй, гончарный круг, с помощью которого у нас появилась возможность создавать весьма точные осесимметричные изделия произвольного профиля. Я до сих пор воспринимаю это как волшебство, смотря на то, как гончар формирует кривую своими руками; то, как эта кривая задаёт форму для всей вазы через вращение колеса:
Простым обобщением гончарного круга является токарный станок. По сути это гончарный круг для дерева или металла. Токарные станки похожи на гончарные колеса, однако заготовка располагается горизонтально, а кривую формирует некоторый острый режущий инструмент. Режущий инструмент также может быть прикреплен к направляющей с некоторым контуром, в результате чего можно производить изделия одинаковой формы.
Станок и гончарный круг могут производить определённый класс тел, которые называются телами вращения. Поверхность тела вращения есть поверхность вращения.
С точки зрения математики поверхность вращения есть результат вращения некоторой кривой, заданной на плоскости, вокруг оси (ось должна лежать на той же плоскости). Полученная поверхность вращения располагается в трехмерном пространстве. Тело вращения есть результат вращения некоторой двумерной области вокруг оси.
Поверхности и тела вращения обычно изучают на втором семестре курса математического анализа – как одну из сфер применения интегрирования. Помню, эта тема показалась мне весьма полезным учебным материалом, ведь это следующий наиболее интуитивный пример концепции интегрирования после площади под графиком, в котором, правда, используется одиночный интеграл.
Вместе с 3D-печатью и Wolfram Language студенты имеют возможность добавить визуальное представление и опыт проектирования к теории и математической интуиции, которые они уже имеют. И, как будет показано далее, совсем не обязательно что-то знать из области программирования или уметь производить расчёты для того, чтобы использовать «виртуальный гончарный круг» в Wolfram|Alpha! И, повинуясь зову гончарного круга, давайте сделаем какую-нибудь чашку!
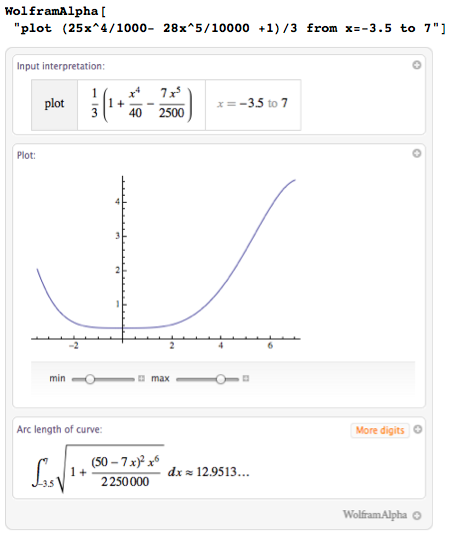
После некоторого изучения различных функций в Wolfram|Alpha (ладно, признаюсь, тут я использовал Wolfram Language, чтобы иметь возможность интерактивного управления формой кривой) я нашёл интересную кандидатуру на роль кривой для нашей чашки – из неё должно получиться нечто вроде коктейльного бокала:
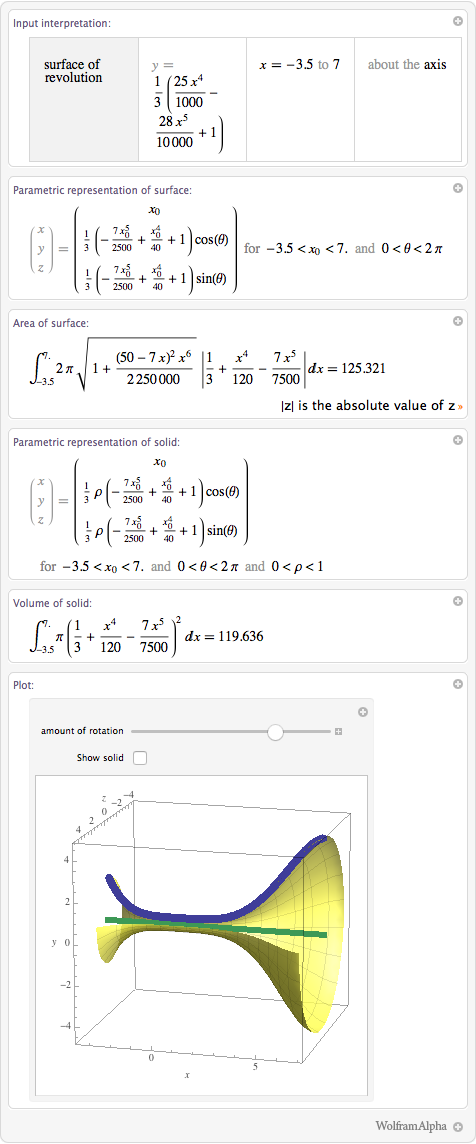
Теперь я могу просто поменять plot (построить) на revolve (провращать), а Wolfram|Alpha расскажет мне о моём бокале и покажет его изображение:
В дополнение к уравнениям, которые определяют тело и поверхность, я получаю значение объёма внутри тела и площадь его поверхности. Объем около 120 – это означает, что если в качестве единицы измерения мы использовали сантиметры, то мой бокал будет вмещать в себя 120 мл (120 куб.см).
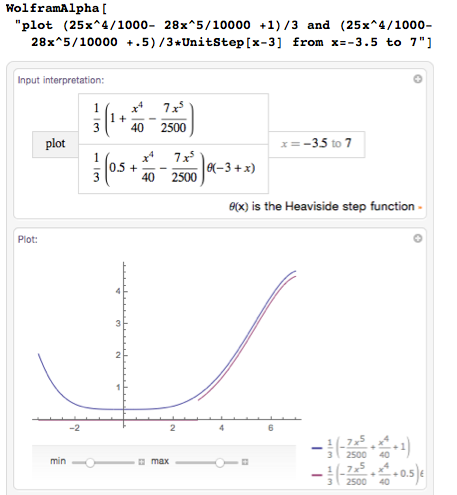
Однако этот объем включает в себя и то, что заключено в ножке бокала и в его основании. Часть этого пространства необходимо зарезервировать для стекла (или другого материала, из которого будет изготовлен бокал). Потому давайте добавим внутреннюю кривую – я её задал путем смещения исходной кривой на 1/6 вниз и взятия её на промежутке от 3 до 7:
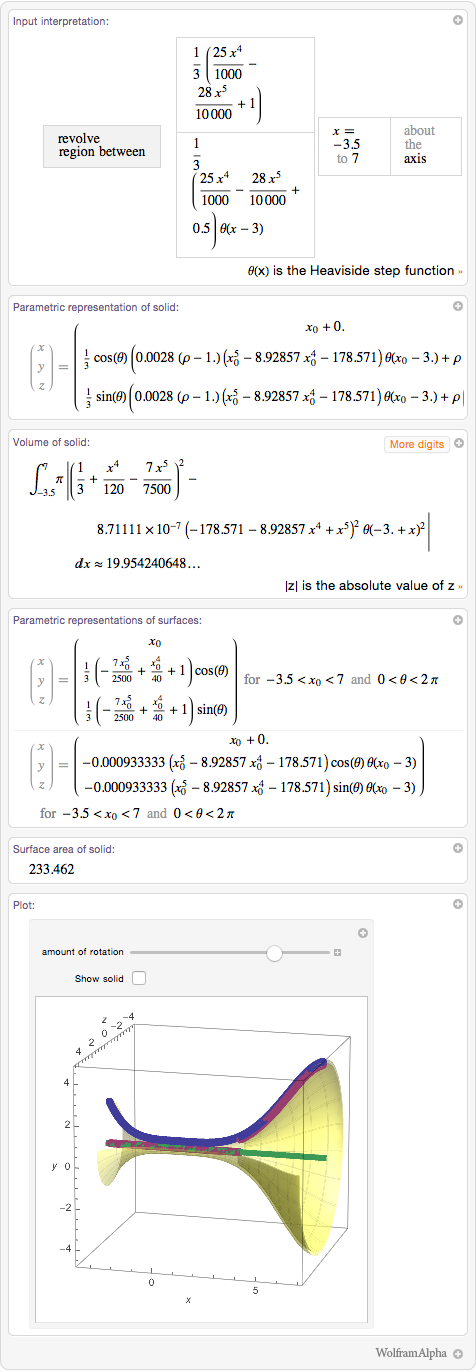
Теперь я мог бы либо распечатать этот график для использования его в качестве шаблона на своем токарном станке (если бы у меня такой был), либо продолжить работать с «виртуальным гончарным колесом»:
Теперь я знаю, сколько материала мне потребуется для производства одного бокала – около 20 куб.см., то есть у нас остаётся около 100 мл пространства для размещаемого в бокале питья. Можно также вычислить то, сколько краски нам нужно потратить для окрашивания бокала. Площадь его поверхности составляет приблизительно 233 см², а на банках с краской обычно указывается то, на покраску какой площади её хватит.
Чтобы распечатать эту чашу через сайт Shapeways, я воспользовался упрощенным способом, о котором в прошлом году писал Виталий Кауров.
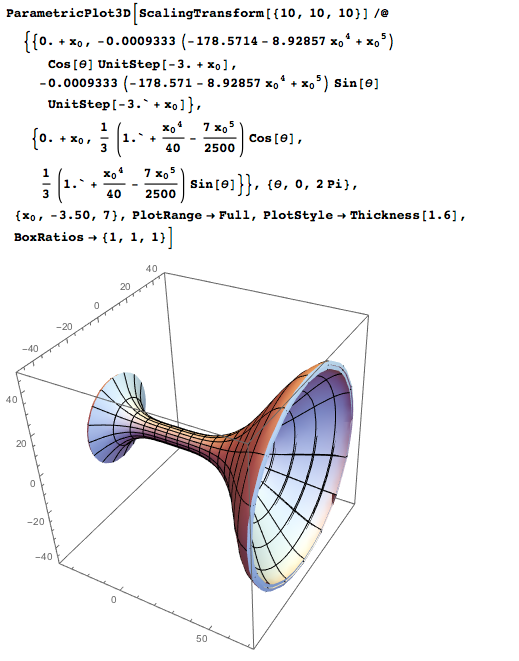
Хоть я и могу построить любую поверхность вращения в Wolfram Language с помощью RevolutionPlot3D, вместо этого я просто скопировал «Параметрическое представление поверхностей» и использовал его в ParametricPlot3D (а если вы хотите реализовать это через Wolfram|Alpha, то скопируйте «Текстовый ввод в Wolfram Language» из «Параметрического представления поверхностей» – часть вывода Wolfram|Alpha). Оказалось, что мне нужно было кое-что поменять, чтобы удовлетворить требованиям Shapeways: во-первых, необходимо было перевести сантиметры в миллиметры, чего я добился, увеличив все размеры в 10 раз (посредством ScalingTransform), а во-вторых мне нужно было задать толщину в 1.6 мм, что я реализовал с помощью PlotStyle:
Единственное, что после этого потребовалось – загрузить чашку в .stl формате на их вебсайт:
И… вуаля! Вот изображение готового бокала, воплощенного в пластике (стоило это всё $23):
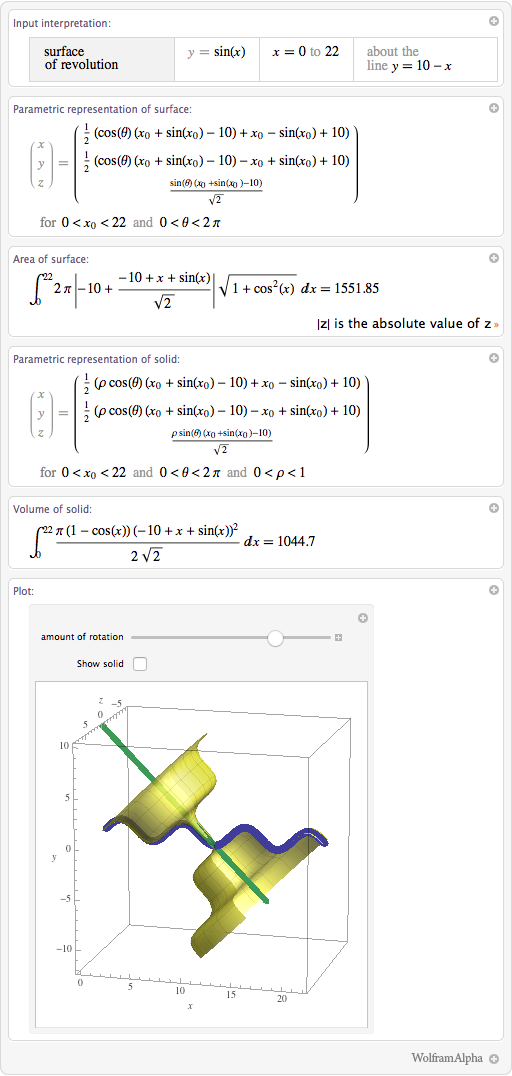
В Wolfram|Alpha можно создавать самые разнообразные поверхности и тела вращения, используя различные функции, оси и параметры вращения:
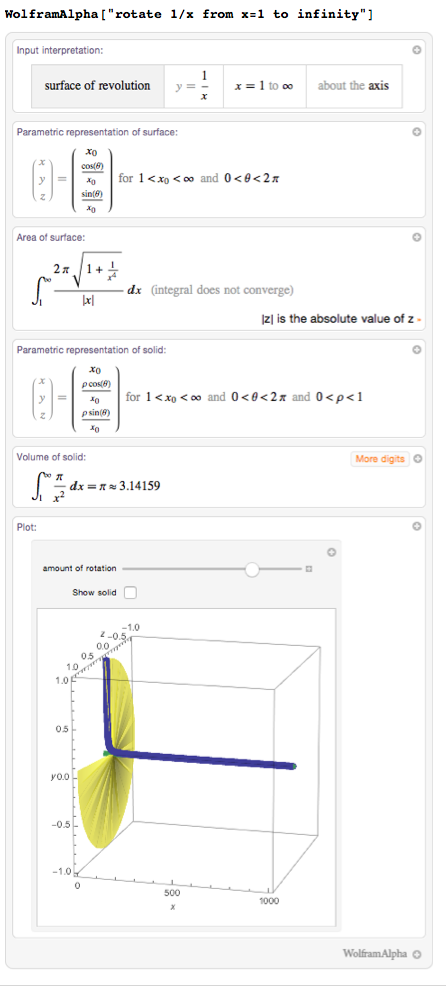
Я могу даже провращать бесконечно длинную часть кривой, что приведёт нас к математическому «парадоксу» под названием рога Гавриила (или труба Торричелли):
Wolfram|Alpha сообщает, что полученный объем равен π, однако площадь поверхности бесконечна! Кажется, из этого следует, что я могу заполнить рог конечным количеством краски, однако этого количества не должно хватить на то, чтобы покрыть всю внутреннюю поверхность – какой-то абсурд получается. Разумеется, слой краски на самом деле не является двумерным, и в некоторый момент трубка сузится настолько, что через неё больше не сможет пройти ни одной молекулы, так что с точки зрения физики мы не имеем никакого парадокса.
Вскоре пользователи Wolfram|Alpha Pro смогут получить доступ к пошаговым решениям задач о нахождении площади и объема поверхности вращения, показывающие, как можно вычислить отдельные составляющие поверхности или объема и объединить их вместе. Я был бы рад услышать от вас идеи о том, как еще можно использовать данную методику.
И вот, держа сейчас этот бокал в руках (отчасти потому, что я не учёл его склонность к опрокидыванию), я предлагаю тост: за творчество и за те инструменты, которые позволяют реализовать наши идеи. Будем!
Как правильно вводить формулы на вольфрам альфа
Основные операции
- Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Знаки сравнения
Логические символы
Основные константы
Основные функции
: x^a
модуль x: abs(x)
Решение уравнений
Чтобы получить решение уравнения вида 
- Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
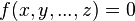

- Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Решение неравенств
Решение в Wolfram Alpha неравенств типа 
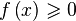

- Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
- Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5<0 или Solve[x^2+y^3-5<0,x] или Solve[x^2+y^3-5<0,y];
- x+y+z+t+p+q>=9.
Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
- Примеры
- x^3+y^3==9&&x+y=1;
- x+y+z+p==1&&x+y-2z+3p=2&&x+y-p=-3;
- Sin[x+y]+Cos[x+y]==Sqrt[3]/4&&x+y²=1;
- Log[x+5]=0&&x+y+z<1.
Построение графиков функций
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


![x in left[ {a,b} right]](https://upload.wikimedia.org/math/7/4/2/742cbcce0d00d20060f55c3603104e64.png)

![y in left[ {c,d} right]](https://upload.wikimedia.org/math/5/3/0/530e43b31b783941629e7b4a8d2c8866.png)
- Примеры
- Plot[x^2+x+2, {x,-1,1}];
- Plot[x^2+x+2, {x,-1,1},{y,-1,5}];
- Plot[Sin[x]^x, {x,-Pi,E}];
- Plot[Sin[x]^x, {x,-Pi,E},{y,0,1}].
Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],{x, a, b}].
- Примеры
- Plot[x&&x^2&&x^3, {x,-1,1},{y,-1,1}];
- Plot[Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}].
Для того, чтобы построить график функции 
![x in left[ {a,b} right],y in left[ {c,d} right]](https://upload.wikimedia.org/math/8/2/b/82b905749a5dce2a347335bbfa1eb8f1.png)


- Примеры
- Plot[Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2}];
- Plot[xy,{x,-4,4},{y,-4,4}].
Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 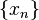
- Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

- Примеры
- Limit[Sin[x]/x, x -> 0];
- Limit[(1-x)/(1+x), x -> −1].
Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- D[x*E^x, x];
- D[x^3*E^x, {x,17}];
- D[x^3*y^2*Sin[x+y], x];
- D[x^3*y^2*Sin[x+y], y],
- D[x/(x+y^4), {x,6}].
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
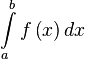
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- Integrate[Sin[x]/x², x];
- Integrate[x^10*ArcSin[x], x];
- Integrate[(x+Sin[x])/x, {x,1,100}];
- Integrate[Log[x^3+1]/x^5, {x,1,Infinity}].
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: {f_1,f_2,…,f_n}, где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
- Примеры
- y»’+y»+y=Sin[x];
- y»+y’+y=ArcSin[x];
- y»+y+y^2=0;
- y»=y, y[0]==0, y'[0]=4;
- y+x*y’=x, y[6]=2;
- y»'[x]+2y»[x]-3y'[x]+y=x, y[0]=1, y[1]=2, y'[1]=2;
- {x’+y’=2, x’-2y’=4}.
Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач. К примеру, если попытаться решить неравенство 
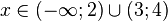
Разложение на множители
Например, разложить на множители
x2/3 — 3x + 12
Запишем как
factor x^2/3 — 3x + 12
и нажимаем равно (=).
Например, разложить на слагаемые
Запишем как
Partial fraction expansion(1-x^2)/(x^3+x)
используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series) или
Series expansion at x=0
Разложить в ряд Лорана:
Laurent expansion z*cos(1/z) at z =0
Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Комплексно сопряженное z*
Египетская дробь:
Egyptian fraction expansion:
11/30=1/3+1/30
parametric plot (3*cos t, sin t, 2t), t=0..2pi
interpolation polynomial {1,4,9,16}
Транспонировать матрицу: transpose {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}
Обратная матрица inverse {{a, b}, {c, d}}
Собственные числа (вектора) матрицы: eigenvalues( ( transpose{{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}})-1/67.42598*({{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}))
Решение СЛАУ : {{8,2,-3,2},{-6,3,-2,1},{3,8,4,-8},{2,1,-6,2}}*{{x_1},{x_2},{x_3},{x_4}}={{102},{-47},{-122},{-24}}
{{-9,5,2},{5,-6,3},{4,1,-5}}*{{x},{y},{z}}={{0},{0},{0}}
Интегральное преобразование Лапласа —- LT
Обратное преобразование Лапласа — ILT
Содержание
WolframAlpha
Wolfram Alpha — база знаний и набор вычислительных алгоритмов, вопросно-ответная система.
Вместо того, чтобы предоставлять ссылки на другие сайты, сервис собирает факты и цифры из разных источников и потом оперирует этими данными для отображения результатов поиска в виде таблиц, графиков и других иллюстраций.
Разработчик Стивен Вольфрам — британский физик, математик и бизнесмен, известный по программе компьютерной алгебры «Mathematica». Сервис запущен в мае 2009.
Построение графиков
График функции одной переменной — команда plot или синоним graph:
plot x^3 - 6x^2 + 4x + 12 graph 3x^2-2xy+y^2=1
С указанием диапазона значений переменной:
plot e^x from x=0 to 10 plot x^2 y^3, x=-1..1, y=0..3
Несколько функций в одной системе координат:
plot sin x, cos x, tan x
Графики действительной и мнимой частей функции:
plot sin(sqrt(-7)x)+19cos(x) for x between -5 and 5
График функции двух переменных (desmos трехмерные графики строить не умеет):
plot sin x cos y 3D plot sin x cos y plot x^2 - 3y^2 - z^2 = 1
Графики комплекснозначных функций двух переменных:
plot sin((x + i y)) cos(y) // выводятся графики действительной и мнимой части
Точки пересечения с осями:
y-intercept of 3x-4y=5 intercepts (x+1)^3
Угловые точки графика функции (точки излома):
corners of x + 2 |sin x| corners sqrt |x-2| - cbrt |x+2|
Асимптоты:
asymptotes (2x^3 + 4x^2 - 9)/(3 - x^2)
Точки перегиба:
inflection points of x+sin(x)
Числовые ряды — показывает решение на числовой оси в графическом виде и в виде интервалов:
number line 2, 3, 5, 7, 11, 13
plot {2, 3, 5, 7, 11, 13}
number line x^2>5, 0<=x<3
sum j^2, j=1 to 100 // сумма
product j^2, j=1 to 100 // произведение
Графики специальных функций:
plot Ai(x) // Airy function polar plot r = Ai(theta)
Графики в полярной системе координат
в desmos букву надо выбирать на виртуальной клавиатуре либо печатать слово theta — сделает автозамену
polar plot r=1+cos theta polar plot r=theta, theta=0 to 8 pi polar plot r^2 = 4/theta polar plot 2 cos(4 * theta) polar plot r = 3 sin(theta)/theta
Параметрические графики
Воспользуйтесь параметрическим графиком, если можете выразить координаты x, y или x, y, z в каждой точке кривой как функцию одного или более параметров. Например, окружность параметрически задается так: $x=sin(t), y=cos(t), t∈[0;2π]$
parametric plot (1-t, t^2) parametric plot (t sin(t), tcos(t)), t in 0..5pi // спираль parametric plot (2cos(t)+cos(2t), 2sin(t)−sin(2t)), t in 0..2pi // дельтоида 3d parametric plot (r cos(t), r sin(t), log(sqrt(r))), t in 0..2pi, r in 0.1..1
Графическое решение неравенств
Неравенства (desmos умеет решать неравенства, но конкретно это неравенство с кубом не смог решить):
plot |x|^3+|y|^3<1
Системы неравенств:
plot x^2+y^2<1 and y>x
Площади фигур
Площадь фигуры, ограниченной линиями:
compute the area between y=|x| and y=x^2-6
Площадь фигуры, ограниченной замкнутой кривой:
area inside x^2 -2xy + 4y^2 -x+y= 4
Алгебра
Уравнения
Решить уравнение (в комплексных числах):
solve x^2 + 4x + 6 = 0
Решить систему:
x+y=10, x-y=4
или {x+y=10, x-y=4}
Решать уравнение с параметрами (выразить x через a,b,c):
solve a x^2 + b x + c = 0 for x solve a = b + c for b solve |x^2-3x|-a for x // нажать more roots, т.к. показывает не все корни
Решить уравнение в целых числах (Диофантово уравнение):
solve 3x+4y=5 over the integers
Преобразовать выражение
Упростить выражение:
simplify x^5-20x^4+163x^3-676x^2+1424x-1209 1/(1+sqrt(2)) simplify cos(arcsin(x)/2)
Разложение многочлена на множители:
factor 2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48
Раскрыть скобки:
expand (x+1)^3
Выделение квадрата двучлена:
complete the square 3x^2-2x-3
Числа
Если ввести число, например, 28, выдает всё об этом числе — простое ли оно, разложение на множители, перевод в двоичную систему, римские цифры, разложение в сумму квадратов и прочее.
Ввести число, затем нажать кнопку More digits — выдаст все числа от 01 до 99
1/9801
Разложить на разряды, число прописью:
place values of 6135
Периодическую дробь представить обычной:
.03571428571428... (0.8333...)(0.1111...)/(0.22111111...)
Это рациональное/иррациональное число:
Is sqrt(1-1/5+1/9) a rational number? is (sqrt(8)-sqrt(2))^2 irrational?
Последняя цифра числа:
last digit of 9^9^9 last nonzero digit of 178,000! // также выдает сколько нулей в конце
Вычисления высокой точности:
141(2^141) + 1 // 45 знаков 2009! // факториал pi to 1000 digits
Показать число или интервал на числовой оси:
number line e^3 show x^3-4x+1>0 on a number line // решает неравенство
Цепные дроби:
continued fraction 12/67
Русские название цифр:
russian numeral names
Название числа (число прописью):
write out 10^39 spell 40
Константы
Выдать 200 цифр константы:
Conway constant to 200 digits golden ratio - 1/(golden ratio) // золотое сечение silver ratio series representations of pi // разложения в ряд
Выразить число через константы:
express 4.8675 through pi and e
Интервалы
[3,8) intervals [0,1), (1,oo) interval [-sqrt(5), 1+sqrt(5)]
Простые числа. Делители
Простые числа
Выдать все простые числа, меньшие 100:
primes <= 100 primes between 100,000 and 101,000 // все простые числа из диапазона prime closest to 169743212304 // простое число, ближайшее к указанному
Выдать миллионное простое число:
1,000,000th prime
Простое ли число?
Is 10001 prime?
Таблица простых чисел с 4-го по 17-е:
table[prime(n), {n=4,17}]

Частичные суммы простых чисел
Accumulate[Table[Prime[n], {n, 1, 19}]]

Выдать указанную пару простых чиел-близнецов:
1000th twin prime
Число Мерсенна:
20th Mersenne prime
Факторизация
Разложить на простые множители:
factor 70560
Показать все делители числа (не только простые):
divisors 3600
Делится ли число на указанное число?
Is 1729 divisible by 13?
Наибольший общий делитель:
gcd 24, 36, 48, 60
Все общие делители чисел:
common divisors of 360 and 96
Общее кратное чисел:
common multiples of 10, 25
Наименьшее общее кратное чисел (least common multiple):
lcm 9, 12, 21
Можно использовать в выражениях:
gcd(36,10) * lcm(36,10)
Выборки
Мода, среднее выборки, медиана выборки
commonest, mode, mean, median {1,2,3,3,3,4}
См. также
Функции
Область определения (и графически и как интервал):
domain of f(x) = x/(x^2-1) domain of sqrt(sin(x)) domain of f(x,y) = log(1-(x^2+y^2)) // для двух переменных
Область значений:
range of x^2 - x - 1 range of 1/sqrt(x^2+1) restricted to 1<x<4 // с ограничением по x domain and range of (x^2+1)/(x^4-1) // и то и другое domain and range of tan(x) restricted to x>0 domain and range of z = x^2 + y^2 // для двух переменных
Точки разрыва (см. Изучение разрывных функций с помощью WolframAlpha):
discontinuities 1/(x-1) discontinuities 1/((x-1)(x^2-9)) // есть кнопка Show limits
Период функции:
period y=sin(x)*cos(3x)
Четность функций:
what is the parity of sin(x) is sin(x+pi/4)+cos(x+pi/4) an even function? is f(x,y,z)=sin(xyz) an odd function?
Экстремумы:
maximize x(1-x)e^x minimize x^4-x minimize (4 - x^2 - 2y^2)^2 // функция двух переменных extrema calculator // глобальные минимум и максимум
Стационарные (критические) точки:
stationary points 3sin(x/3) // производная равна 0, касательная || Ox
Табулировать функцию:
table[x/(x+1),{x,0,5,1}]

Уравнение касательной в точке:
tangent line x^2, x=1 tangent line to y=sinx+lnx at x=3e
Пределы
Limit[Sin[x]/x, x -> 0] // Предел функции
Производная
D[x^3*E^x, {x,1}] // Первая производная по переменной x
D[x^3*E^x, {x,2}] // Вторая производная
d/dx (5x^7+4x^6-3)
d^2/dx^2 x^2e^cosx // второго порядка
d/dx x^2e^cosx, x=pi // значение производной в точке
Сравнить функцию и ее производную
x^3-6 x^2+4 x+12 vs d/dx x^3-6 x^2+4 x+12
Таблица производных
table[d^n/dx^n cosx^5,{n,0,5,1}] // таблица производных до 5-го порядка
table d^n/dx^n (x^3+(-6 x^2+4 x+12)) for n = 1...4
Интеграл
integral, primitive, integrate
Integrate[f[x], {x, a, b}]
Integrate f(x), x=a..b
Integrate Log[x^3+1]/x^5, x=1..Infinity // заодно и неопределенный
int x^2/(x^2+1)^2 dx, x=-infinity..infinity // несобственный интеграл
integrate by parts x^2/(x^2+1) // по частям
Дифференциальные уравнения
Геометрия
Треугольник:
5, 12, 13 triangle triangle 5, 12, 13 triangle with vertices (0,0), (3,4), (4,3) isosceles right triangle, area 1 // прямоугольный равнобедренный nine point circle of triangle (1,1)(2,4)(3,3) // окружность 9 точек incircle of triangle 13,14,15 // вписанная окружность SAS 3 60deg 4 // треугольник по стороне-углу-стороне area of an equilateral triangle with side length a // найти площадь area of triangle, sides a,b,b law of cosines // калькулятор теоремы косинусов law of sines a=6cm, b=8cm, alpha=40deg // теорема синусов
Окружность:
circle, diameter=10
Кольцо:
annulus, inner radius=2, outer radius=5
Угол на единичной окружности:
find the reference angle for 300 degrees
Шестиугольник:
hexagon, perimeter=100
Ромб:
area of rhombus, diagonals 10 and 16
Правильный n-угольник (полигон):
19-gon 15-sided polygon // число диагоналей, углы, диаметр, площадь и прочее regular 7-gon // 7-угольник regular pentadecagon vs triangle // сравнение двух полигонов polygon interior angle // внутренний угол
Вписанная окружность:
incircle of regular 7-gon
Описанная окружность:
circumcircle of triangle a, b, c circumradius // радиус описанной окружности
Стереометрия:
cone // конус What is the radius of a cone with volume v and height 7 cone volume, radius=sqrt(3) // объем конуса sphere, surface area=1 // шар cylinder, radius=3, height=4 // цилиндр
Разное
Сгенерировать безопасный пароль:
generate password password 10 chars
QR-код:
QR code for knitting-club
Мой IP-адрес:
my ip
Перевод единиц измерения:
5 inches in cm
Численные методы
Решить методом Ньютона:
using Newton's method solve x cos x = 0
Метод половинного деления (рисует диаграмму поиска корня):
find root of 2 with bisection method
Метод секущих:
using secant method solve x^3-2 at x1=-3 and x2=3
Интегрирование методом трапеций:
5 interval trapezoidal rule integrate sinx cosx on [0,4]
Комбинаторика
compute binomial coefficients (combinations):
30 choose 18
Перестановки:
permutations of {a, b, c, d}
Разбиения числа:
integer partitions of 10
Число Стирлинга:
S1(8, 4)
Эксперименты по теории вероятностей
Wolfram|Alpha позволяет сделать эксперименты более наглядными, заменяя монеты, карты и кубики их более абстрактными аналогами — математическими многосторонними игральными костями (dice).
двусторонняя «игральная кость» — 2-sided dice : этот эксперимент генерирует два случайных значения 1 и 2: 1 — соответствует гербу «Г», а 2 — решке «Р».
1 2-sided dice — одна «монета»
Есть кнопка «Roll again» — симулятор «бросания монеты».
Выше нее выводится график распределения вероятностей случайной величины и ее числовые характеристики: математическое ожидание (expected value), средне-квадратическое отклонение (standard deviation) и дисперсию (variance).
Эксперимент с двумя монетами имитируется с помощью следующего запроса:
2 2-sided dice
Если «бросить» пять монет одновременно, то получим, кроме уже привычного результата — набора из пяти двоичных значений, еще и некоторые вероятности, в том числе, вероятности некоторых знаменитых карточных комбинаций (нажать кнопку More). Фулхауз, малый стрит, большой стрит, две пары.
5 2-sided dice

Четырехсторонняя кость (4-sided dice) генерирует случайные значения 1, 2, 3 и 4. Эти значения можно интерпретировать, как четыре карточных масти.
Обычный игральный кубик:
1 6-sided dice
Две шестигранные кости — считайте, что два кубика брошены одновременно.
2 6-sided dice
Семь шестигранных кубиков одновременно! Здесь уже интересно посмотреть не только на результат виртуального эксперимента, но и на график статистического распределения вероятностей возможных значений суммы очков, выпавших на кубиках (в диапазоне от 7 до 42) — то, что в реальном эксперименте установить довольно…. утомительно.


Одна 9-гранная кость. «Бросить» такую кость — то же самое, что тянуть одну карту из колоды на 36 карт (четыре масти), если интересует, какая карта по рангу попадется.
1 9-sided dice
Последовательности
OEIS A000219
Фиббоначчи:
sequence of Fibonacci numbers
Предел последовательности
limit (1+1/n)^n as n->infinity
Пытается распознавать последовательности:
5, 14, 23, 32, 41, ... // выдает формулу 1, 4, 9, 16, 25, ...
Суммы, произведения:
1+2+3+...+10 3+12+27+...+300 1/2 + 1/4 + 1/8 + 1/16 + ... 2 * 4 * 6 * ... * 36
Рекуррентную формулу преобразовать в обычную:
g(0)=1, g(n+1)=n^2+g(n) f(n)=f(n-1)+f(n-2), f(1)=1, f(2)=2
Аналитическая геометрия. Координаты
Прямая по двум точкам:
line through (-3,-1) and (3,5) line through (1,2) and (2,1), line through (2,-1) and (3,5) // сразу две x-intercept line through (-3,-1) and (3,5) // пересечение с осью Ox line through (-3,-1) and (3,5) slope // угловой коэффициент line x=2, line x+y=3
Построить прямую по точке пересечения с осью Oy и угловому коэффициенту:
line, slope=-2, y-intercept=3
Треугольник по трем уравнениям сторон:
line x=2, line y=3, line 3x+2y=6
Квадрат:
square s=5 diagonal // диагональ квадрата со стороной 5
Окружность:
circle of radius 2 with center (0,-2) circle (3,4) r=5 // окружность по радиусу и центру circle center (0,0) r=1 image // изображение единичной окружности circle through (0,0), (1,0), (0,1) // по трем точкам circle center (2,1) through (4,3) // по точке и центру x^2+y^2-4x-6y-12=0 center, radius // определить центр и радиус
Пересечение фигур:
intersection circle (2,3) r=5, line (-3,-1) (4,6) // прямой и окружности intersection circle center (2,3) r=5 and triangle (3,-3) (-4,3) (5,8) // две прямые заданы точкой и угловым коэффициентом, точка их пересечения находится: intersection line slope=-2, y-intercept=3, line slope=2, y-intercept=1
Парабола:
parabola (y-2)^2=4x directrix of parabola x^2+3y=16 parabola with focus (3,4) and vertex (-4,5)
Эллипс:
ellipse with semiaxes 2,5 centered at (3,0) focal parameter of an ellipse with semiaxes 4,3
Гипербола:
hyperbola with center (100, 200) and focus (110, 180)
Касательная:
tangent to x e^-x^2 at x=1/3 tangent to x^2-y^2=5 at (x,y)=(3,2) tangent line to x^2 at x=1
Сумма векторов:
vector {1,3} + {5,4} // рисует правило параллелограмма
{1,3} + {5,4} // просто складывает
vector {1,3,0} + {5,4,-1} // рисует параллелепипед
Расстояние между точками:
distance {1,3,0} to {5,4,-1}
Середина отрезка:
midpoint of (-3,-1) and (3,5)
Тригонометрия
Явное указание — угол в градусах:
cos(30degrees) cos(30 deg) // воспринимает как градусы без уточнений
Явное указание — угол в радианах:
cos(30radians) cos(30rad) // догадывается, что это тоже радианы cos(30 r) // считает, что r - переменная sin(pi/2) // наличие pi заставляет интерпретировать в радианах
Секанс:
sec(5x)
Синус суммы:
expand sin(x+y+z)
Синус учетверенного аргумента:
expand sin(4x)
Решить тригонометрическое уравнение:
sin x + cos x = 1
Теорема косинусов:
law of cosines
Теорема синусов:
law of sines a=6cm, b=8cm, alpha=40deg
Период:
period y=sin(x)*cos(3x)
Графы
Логика
p and q xor r // выдает все об этом логическом выражении venn diagram p and q (a intersection b) union c
Таблица истинности:
truth table p xor q xor r
WolframAlpha
Задачи алгебры, решаемые WolframAlpha
Wolfram Alpha позволяет:
- Решать уравнения
- Решать системы уравнений
- Решать уравнения с параметром
- Вычислять свойства многочленов с несколькими переменными
- Раскладывать многочлены на многочлены меньшего порядка
- Упрощать выражения
- Выделять квадрат из выражения
- Раскладывать дроби на простейшие дроби
- Вычислять свойства матриц
- Складывать, вычитать и умножать матрицы
- Вычислять след матрицы
- Вычислять определитель матриц
- Вычислять обратную матрицу
- Вычислять собственный вектор матрицы
- Приводить матрицу к ступенчатому виду
- Приводить матрицу к диагональному виду
Задачи математического анализа, решаемые WolframAlpha
- Вычислять пределы функций
- Вычислять пределы последовательностей
- Вычислять производные
- Вычислять определенные и неопределенные интегралы
- Решать дифференциальные уравнения
- Решать системы дифференциальных уравнений
Задачи геометрии, решаемые WolframAlpha
- Решение задач планиметрии
- Решать задачи стереометрии
- Решать задачи с координатами
Особенности, различные способы решения задач с помощью WolframAlpha
Wolfram Alpha позволяет решать задачи, как аналитическим методом, так и графическим.
Алгоритмы решения задач с помощью WolframAlpha
- Определить, к какому разделу математики относится задача
- Выбрать метод решения задачи
- Составить математическую модель
- Определить необходимые для решения задачи с помощью Wolfram Alpha функции
- Ввести формулу и исходные данные
- Получить результат
- Провести анализ полученного результата
Особенности, достоинства и недостатки WolframAlpha
Главными достоинствами Wolfram Alpha являются:
- Наличие бесплатного функционала
- Возможность работы с любого устройства через браузер.
Главные недостатки Wolfram Alpha:
- Необходимость постоянного подключения к интернету для работы
- Наличие платного функционала
Задачи
Задачи из алгебры
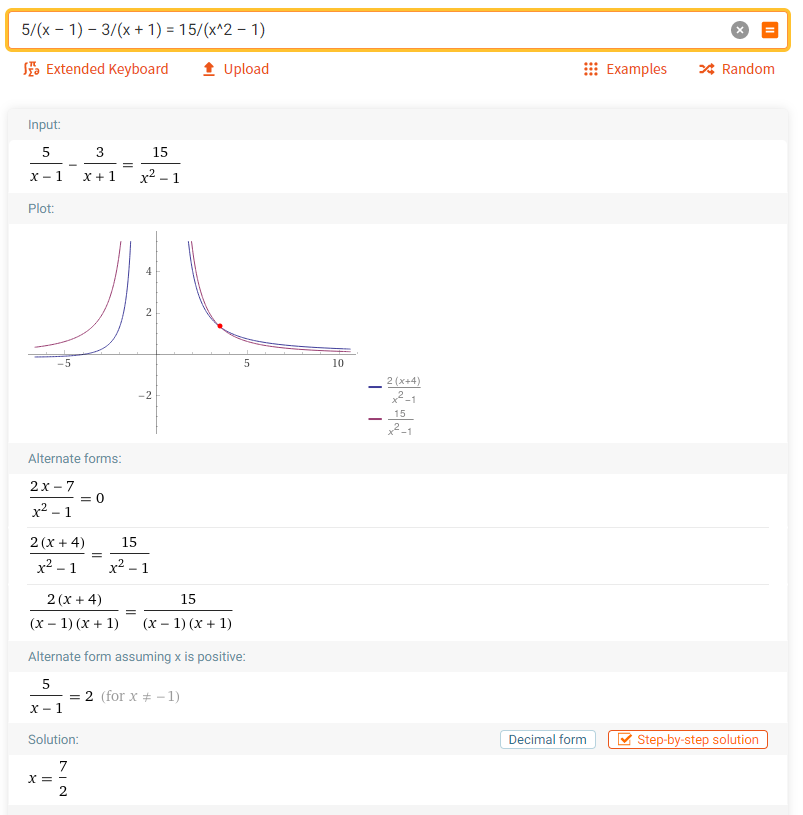
1. Решить уравнение
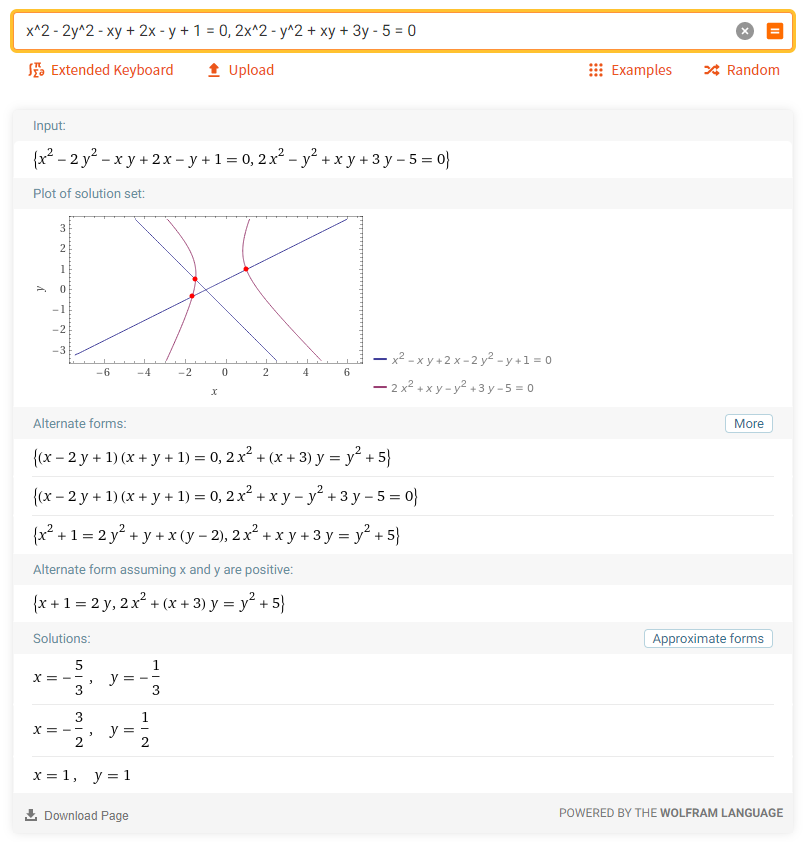
2. Решить систему уравнений:
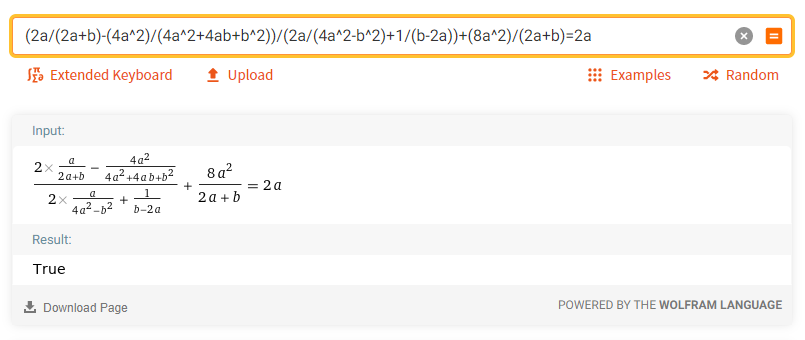
3. Доказать тождество
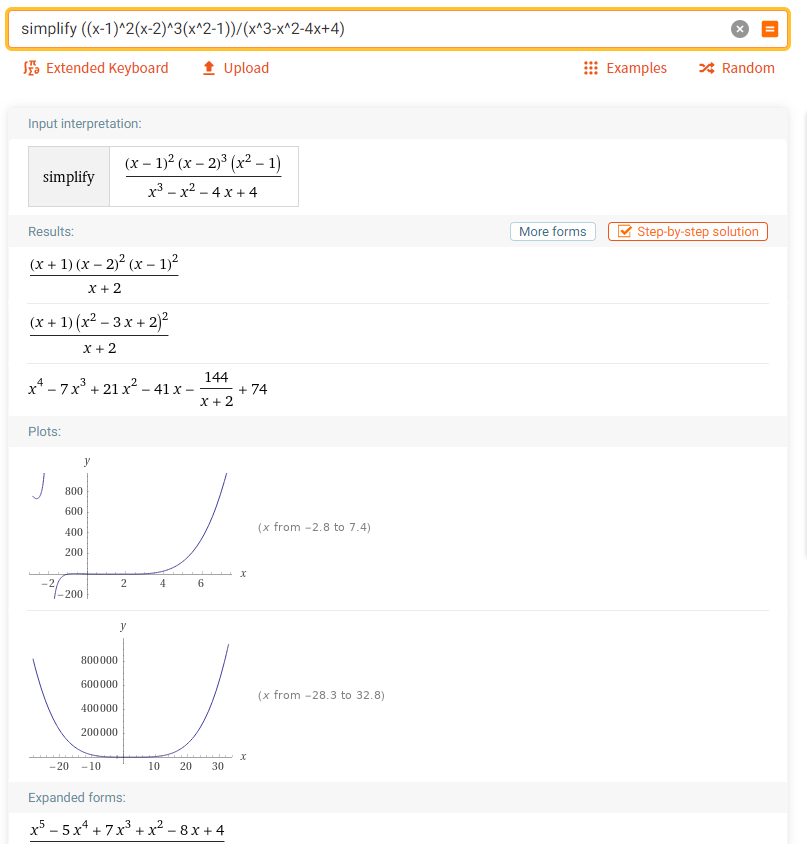
4. Упростить выражение
5. Вычислить определитель матицы:
Задачи из математического анализа
1. Найти производную функции
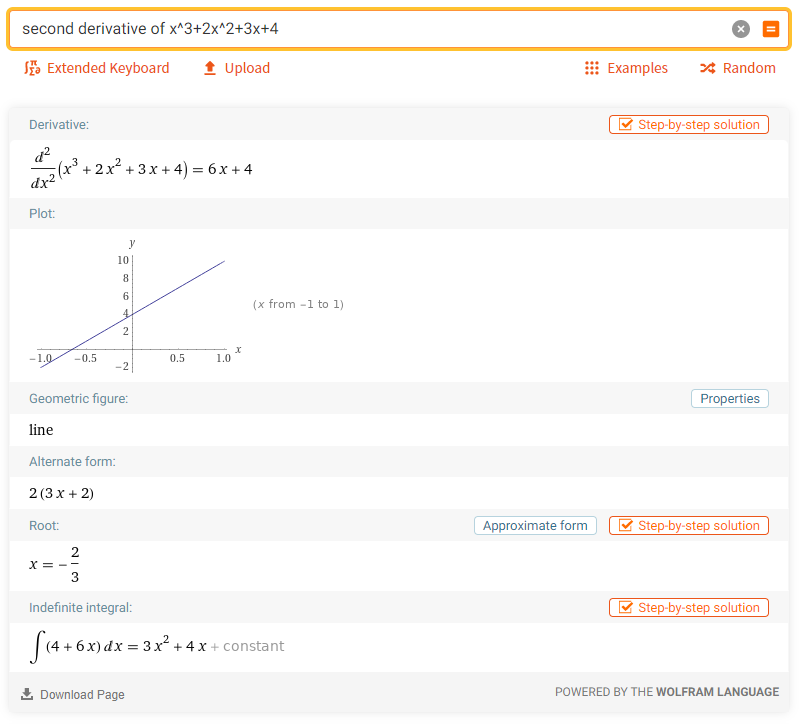
2. Найти производную второго порядка функции
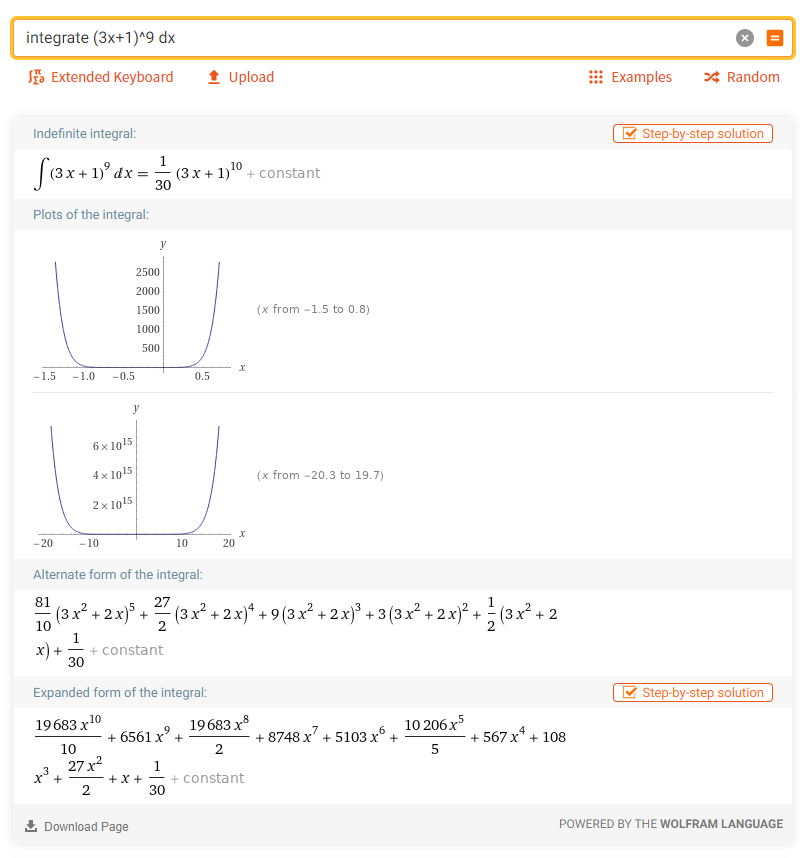
3. Вычислить неопределённый интеграл
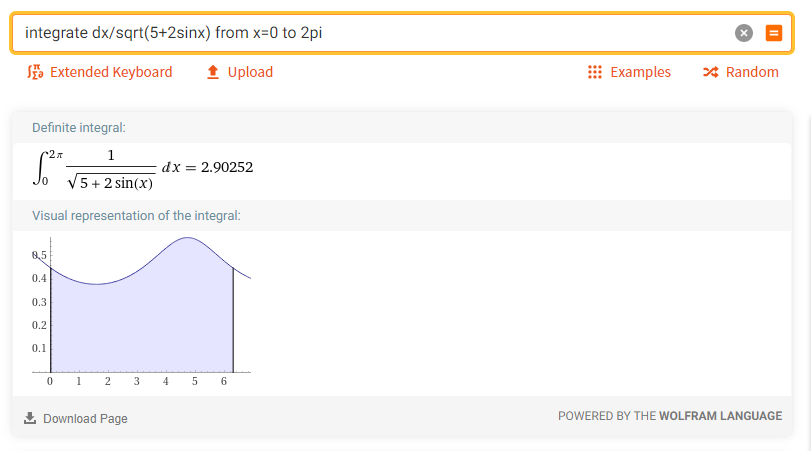
4. Вычислить определённый интеграл
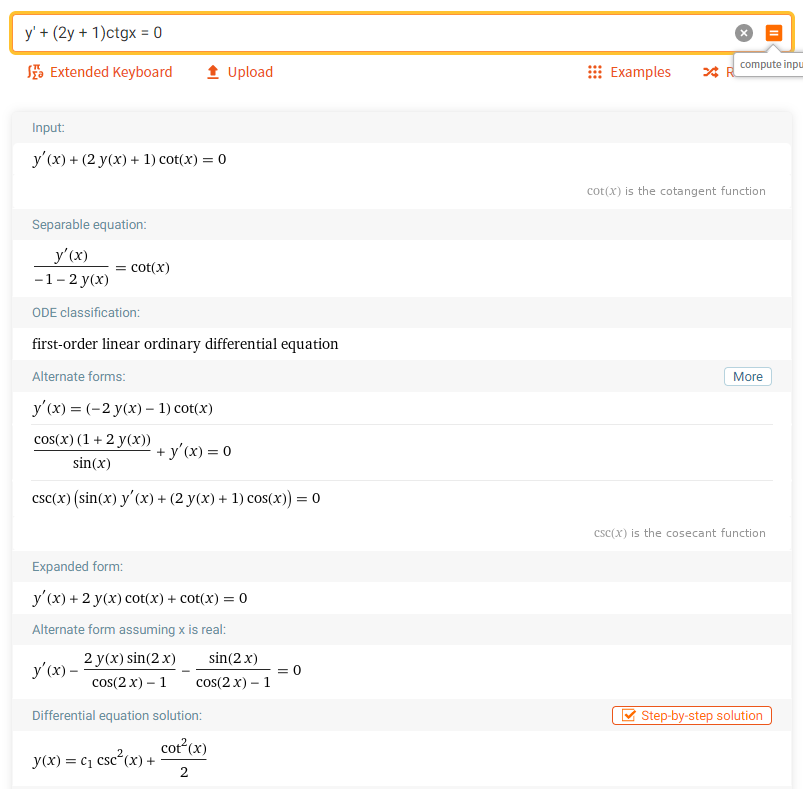
5. Найти корни дифференциального уравнения
Задачи из геометрии
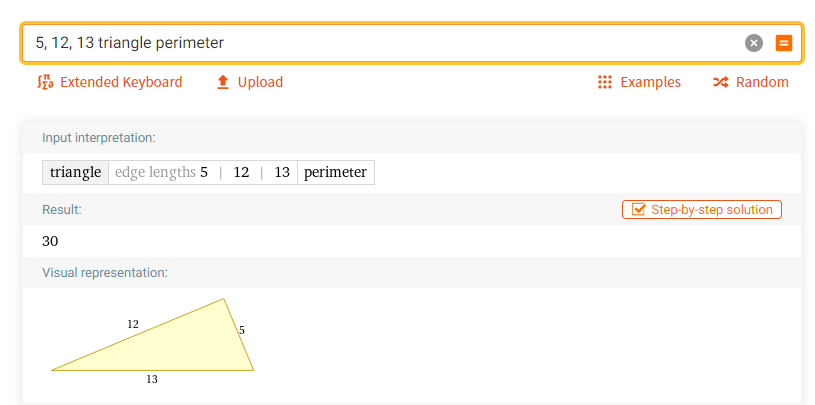
1. Найти периметр треугольника со сторонами 13, 12 и 5:
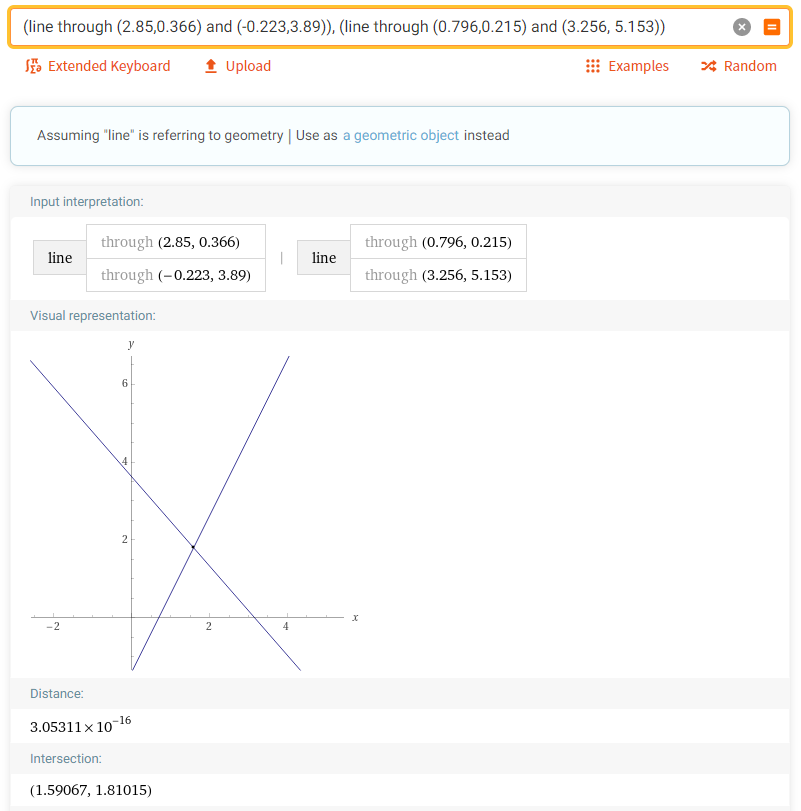
2. Найти пересечение первой прямой, проходящей через точки: (2.85,0.366) и (-0.223,3.89), и второй прямой, проходящей через точки: (0.796,0.215) и (3.256, 5.153):
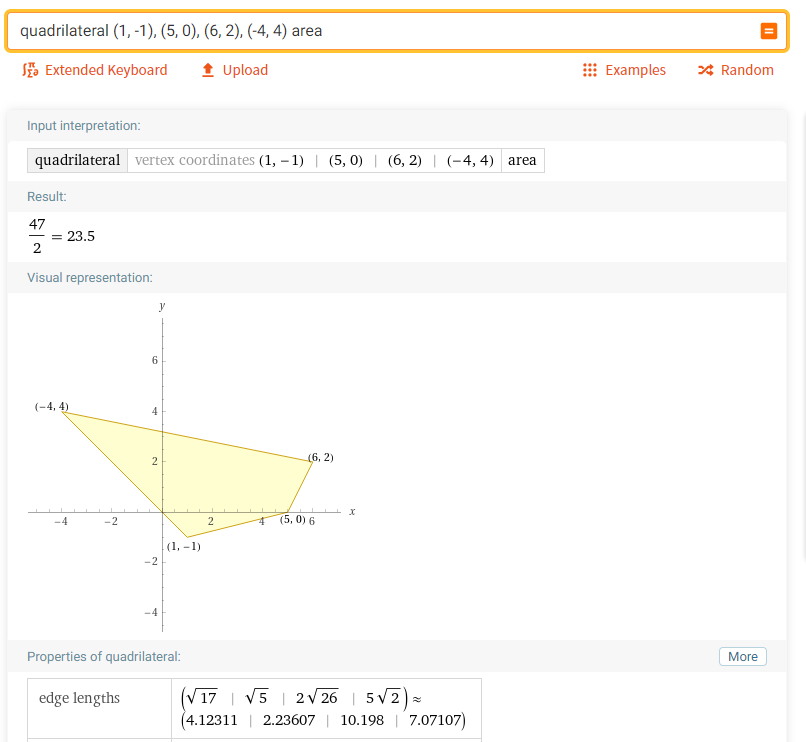
3. Найти площадь четырёхугольника с координатами вершин; (1, -1), (5, 0), (6, 2), (-4, 4):
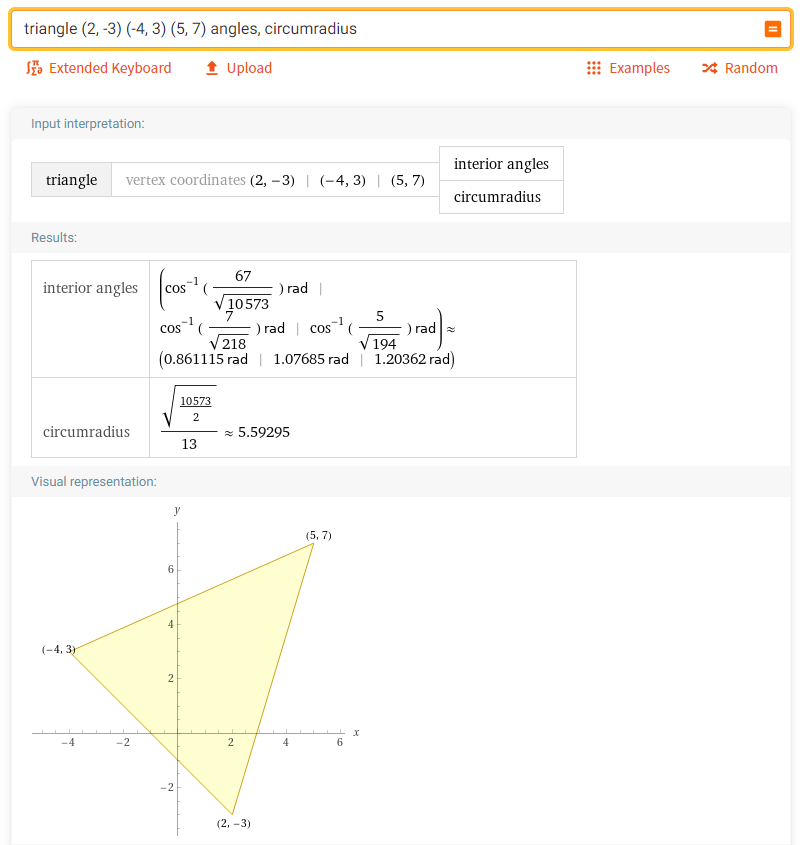
4. Определить углы и радиус вписанной окружности треугольника с вершинами (-4, 3), (5, 7) и (2, -3):
5. Найти диагонали четырёхугольника с вершинами в точках (2, -3) (5, 7) (-7, 9) (-4, 3):





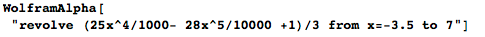
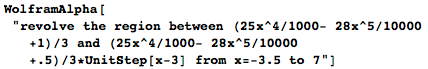


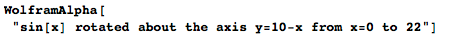

 : x^a
: x^a