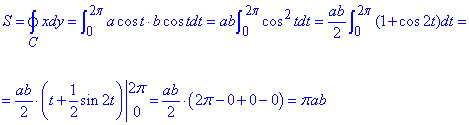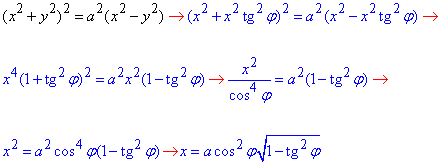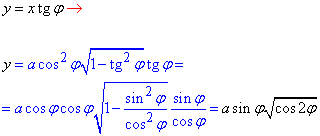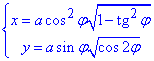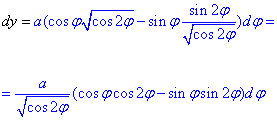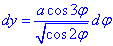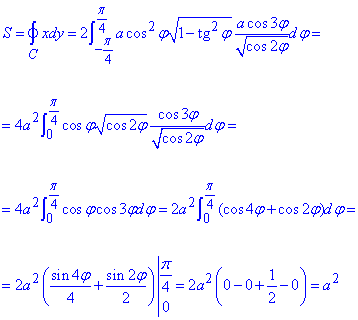3.11.1. Вычисление площадей плоских фигур
Площадь
плоских фигур произвольной формы можно
находить по разному. Начнем с задач о
вычислении площадей с помощью линейного
интеграла.
С
истема
декартовых координат.
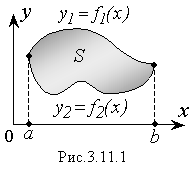
Пусть фигура ограничена линиями,
уравнения которых заданы функциями y1
= f1(x)
и y2
= f2(x)
(Рис. 3.11.1).
Геометрически
линейный определенный интеграл от
функции y
= f(x)
(в предположении, что y
≥ 0) равен площади криволинейной трапеции,
ограниченной сверху графиком y
= f(x),
отрезком [α,b]
оси Oх
и прямыми x
= α,
x
= b,
т.е.:

Исходя
из этого, площадь фигур любой формы
всегда можно представить как, сумму или
разность площадей нескольких криволинейных
трапеций. В частности, площадь фигуры,
изображенной на рисунке 3.11.1, будет
равна:
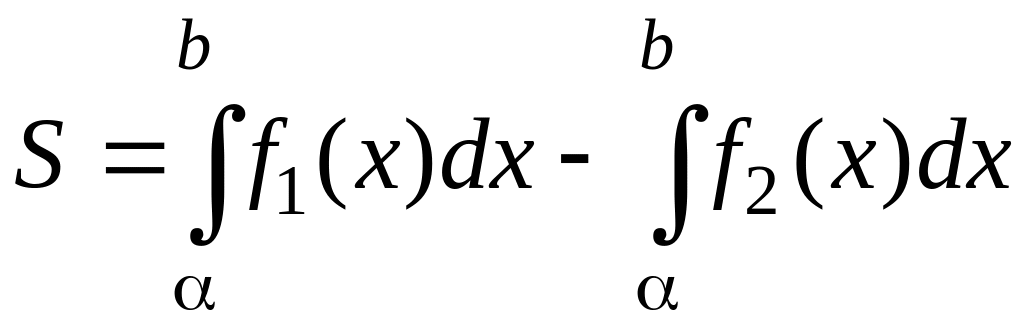
Где
числа α
и b
являются координатой x
для точек пересечения линий y1
= f1(x)
и y2
= f2(x).
П
ример
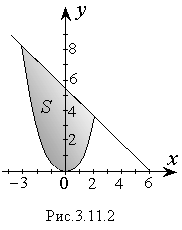
1. Найти
площадь фигуры, ограниченной линиями:
y1
= 6 – x;
y2
= x2
Решение.
Графики функций y
= 6 – x
и y
= x2
изображены на рисунке 3.11.2. Найдем
координату х
для точек
пересечения из условия: y1
= y2
6
– x
= x2
x2
+ x
– 6 = 0
Решая квадратное
уравнение, получим:
Искомая
площадь S
равна разности площадей двух криволинейных
трапеций, ограниченных снизу отрезком
[-3,2] оси Oх,
а сверху графиками функций y1
= 6 – x,
y2
= x2:
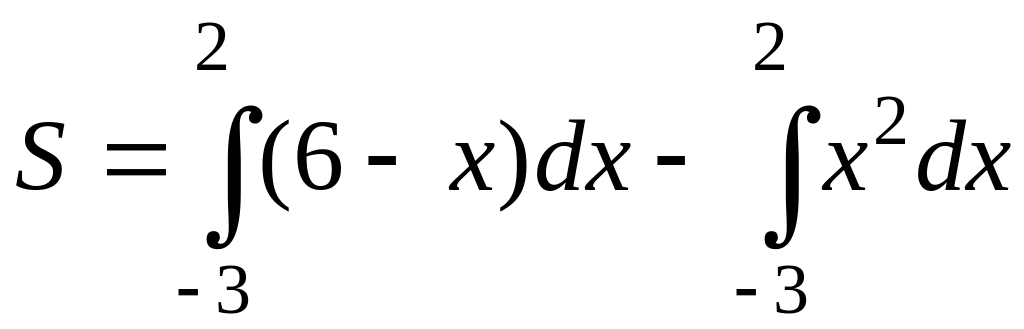
Вычисляя линейные
интегралы, найдем
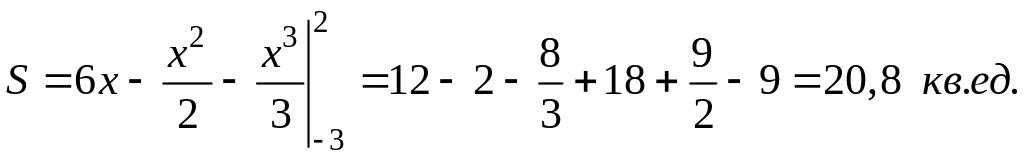
Если
линия y
= f(x)
задана параметрическими
уравнениями
y
= y(t);
x
= x(t),
то
площадь криволинейной трапеции находят
с помощью линейного интеграла, совершая
в нем замену переменной интегрирования
по формуле:

где
t1
и t2
– значения, между которыми изменяется
параметр t.
Эти значения определяют из уравнений
x(t1)
= α,
x(t2)
= b.
Пример
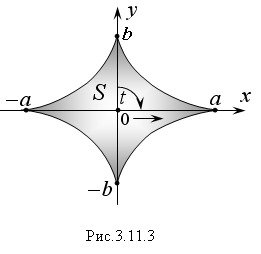
2. Вычислить
площадь, ограниченную астроидой,
уравнение которой задано параметрически:
x
= αcos3t;
y
= bsin3t.
Р
ешение.
График астроиды симметричен относительно
координатных осей Ox
и Oy
(Рис. 5.11.3). Поэтому искомая площадь равна:
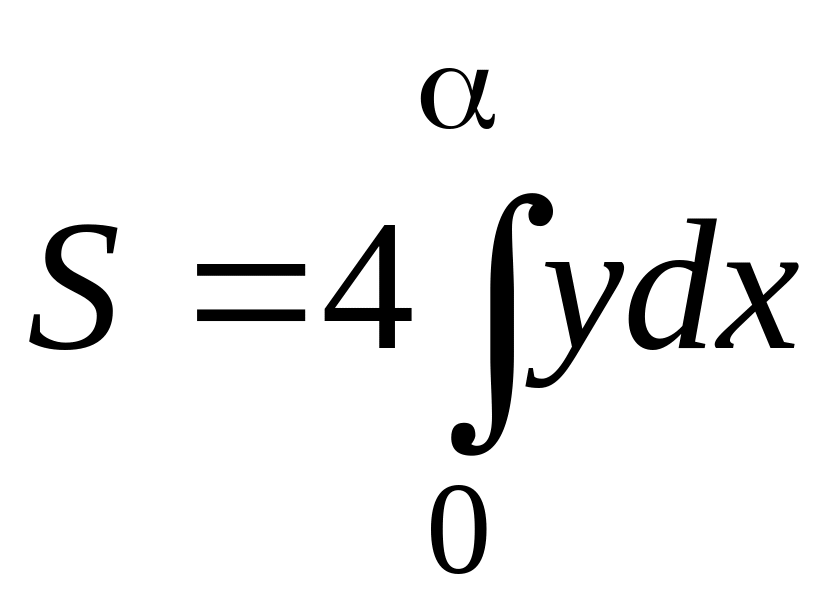
Найдем
пределы изменения параметра t,
когда переменная x
пробегает значения от 0 до α.

Заменим
в линейном интеграле y
и dx
их выражениями через параметр t
из уравнения астроиды. С учетом найденных
пределов для t,
получим:
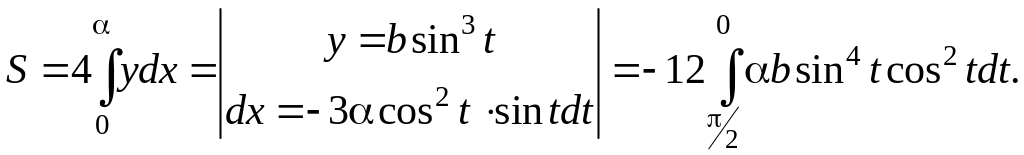
Преобразуем,
подынтегральное выражение и поменяем
местами верхний и нижний пределы:
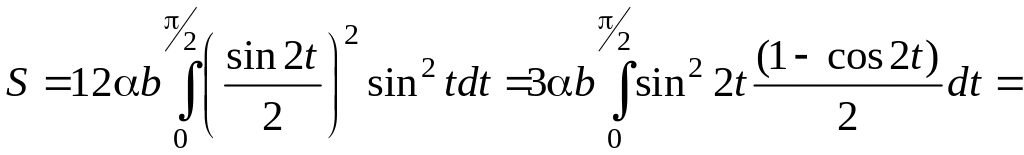

Вычисление последних
интегралов дает
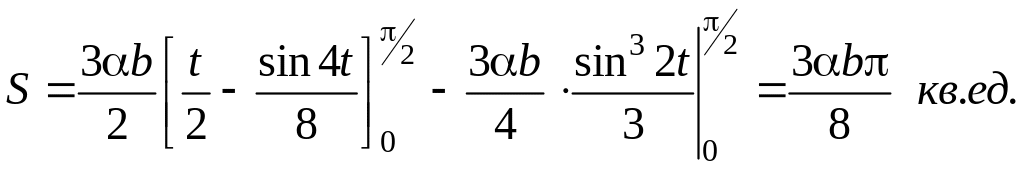
Система
полярных координат. Если
линия, ограничивающая плоскую фигуру,
задана уравнением в полярной системе
координат r
= r(φ),
то вместо площади криволинейной трапеции
берут площадь криволинейного сектора.
Криволинейным
сектором называют фигуру, ограниченную
графиком функции r
= r(φ)
и двумя лучами, проведенными из полюса
до пересечения с линией r
= r(φ).
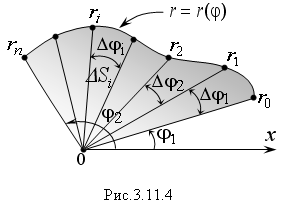
Лучи
образуют с полярной осью углы φ1
и φ2
(Рис. 3.11.4). Площадь такого сектора выражают
одним линейным интегралом. Покажем это.
Разобьем
весь сектор на n-частей
лучами, проведенными из полюса. Центральные
углы частичных криволинейных секторов
будут равны:
Заменим криволинейные
частичные сектора круговыми с радиусами:
Найдем
площадь i-той
части по известной формуле для кругового
сектора
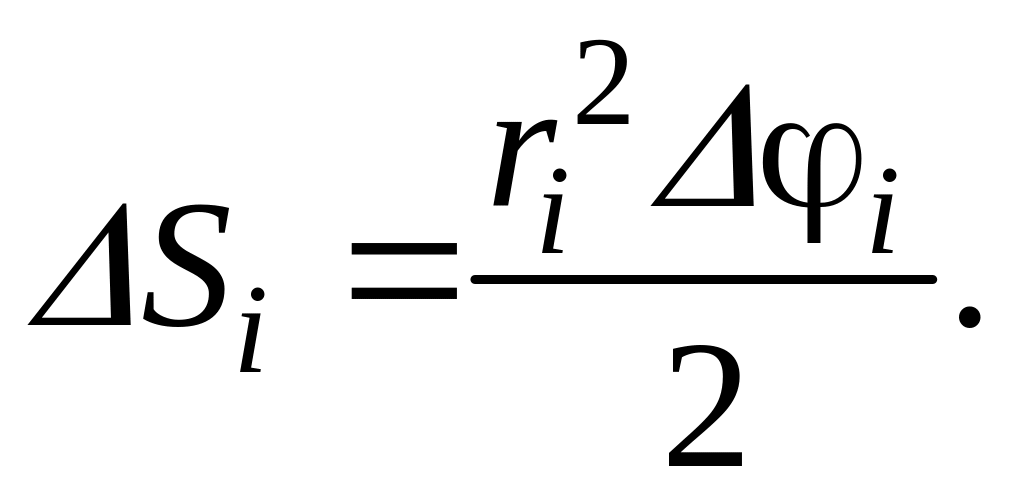
Площадь всей фигуры
приближенно будет равна:
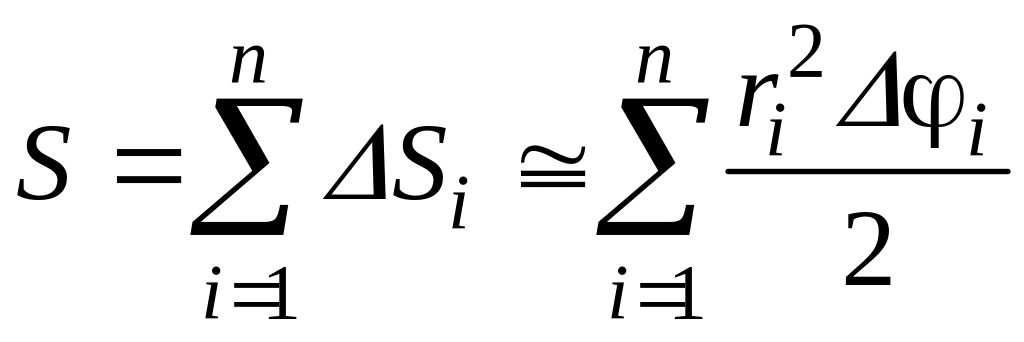
Полученная
сумма является интегральной для функции
В пределе при
частичные круговые сектора будут
совпадать с криволинейными. В результате
точное значение площади всего
криволинейного сектора выразится
линейным интегралом

Пусть
фигура произвольной формы (Рис 3.11.5),
ограничена линиями, уравнения которых
заданы в полярной системе координат:
и
.
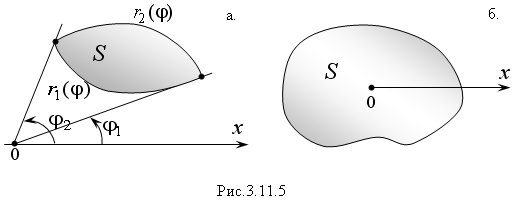
Очевидно,
что ее площадь можно представить как
разность площадей двух криволинейных
секторов, ограниченных графиками функций
и
:
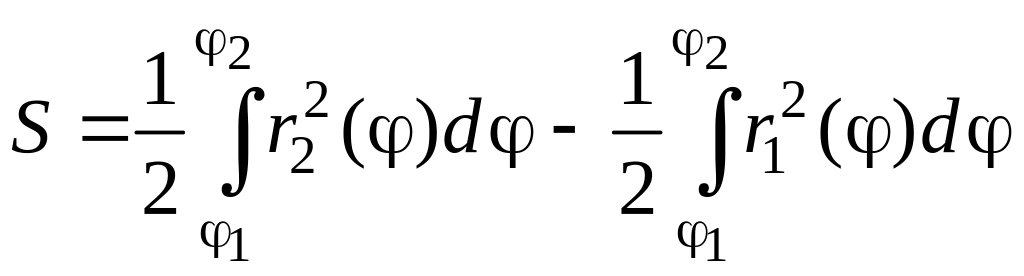
Пределы
интегрирования
и
являются полярными углами для точек
пересечения линий
и
.
Эти пределы находят из условия
.
Если
полюс лежит внутри фигуры (Рис. 3.11.5), то
полярный угол φ будет изменяться от 0
до 2π.
Пример
3. Вычислить
площадь, ограниченную кардиоидой
r
= α(1
+ cosφ)
Решение.
График кардиоиды симметричен относительно
полярной оси. Поэтому можно найти
половину площади, заключенной внутри
кардиоиды, а затем удвоить ее. Тогда
полярный угол φ
будет изменяться от 0 до π. Воспользуемся
формулой для площади криволинейного
сектора:
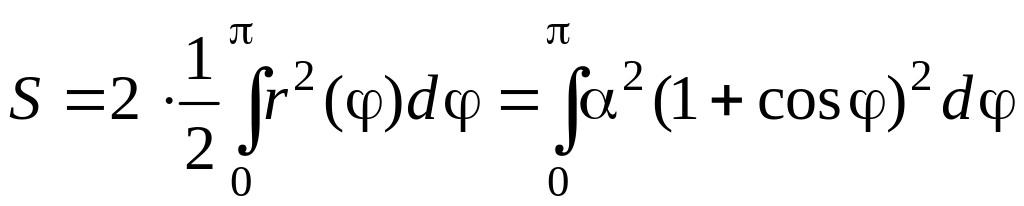
Преобразуем
подынтегральное выражение и найдем
первообразную
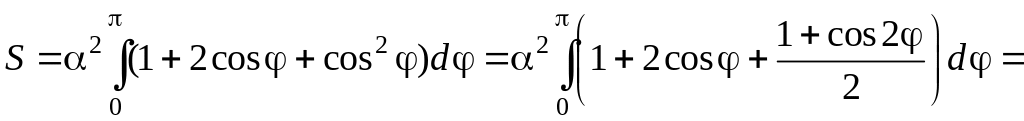
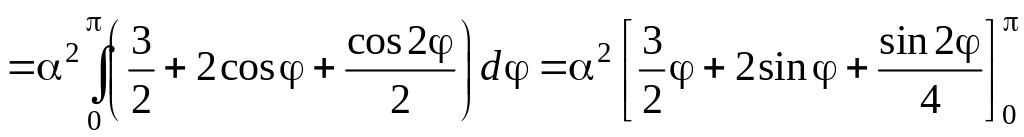
Подставляя верхний
и нижний пределы, окончательно получим:
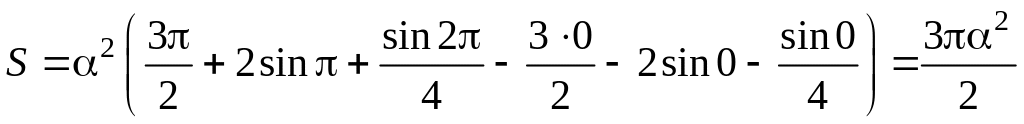
Рассмотрим
другой способ вычисления площадей с
помощью двойного
интеграла.
Определенный
интеграл
по фигуре (или области) (Ω) любого типа
обладает следующим свойством: он равен
размерам области интегрирования (Ω),
если во всех точках
подынтегральная функция равна единицы
Следовательно,
если в двойном интеграле
по плоской области D
положить f(x,y)
≡ 1, то он будет равен размерам D,
т.е. ее площади:
П
ример
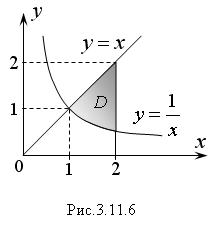
4. Найти
площадь, ограниченную линиями: х
= 2; y
= x;
Решение.
Плоская фигура, площадь которой нужно
найти, изображена на рисунке 3.11.6. Искомая
площадь равна двойному интегралу:
Найдем
координату x
точки пересечения линий y
= x
и
Переменная
х
внутри области D
изменяется от 1 до 2, а переменная y
от своих значений на линии
до значений на линии y
= x.
Переходя к последовательному вычислению
двух линейных интегралов, получим:
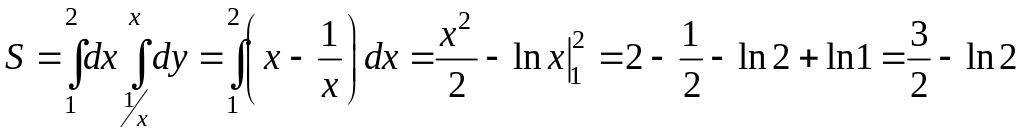
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Compute the surface area of the surface generated by revolving the astroid with parametrization
$$c(t) = left(cos^3 t,sin^3tright)$$ about the $x$-axis
for $tin[0,pi/2]$.
I did not know how to go about answering this question and would really appreciate the help. Thank you in advance.
Tom-Tom
6,7271 gold badge17 silver badges43 bronze badges
asked Apr 30, 2014 at 23:44
$endgroup$
2
$begingroup$
We need to integrate $2pi y,ds$ over the appropriate interval, where
$$ds=sqrt{left(frac{dx}{dt}right)^2+left(frac{dy}{dt}right)^2},dt.$$
The differentiations are straightforward. The $ds$ simplifies to $3|sin tcos t|,dt$, and from $0$ to $pi/2$ there is no issue of signs. So we want
$$int_0^{pi/2} 6pi sin^4 tcos t,dt.$$
Let $u=sin t$, or just write down an antiderivative. The surface area is $frac{6pi}{5}$.
answered Apr 30, 2014 at 23:56
André NicolasAndré Nicolas
499k47 gold badges537 silver badges970 bronze badges
$endgroup$
2
$begingroup$
We know $S = int^{pi/2}_0 2pi yds$ where $S$ is the surface area and $ds = sqrt{(frac{dx}{dt})^2 + (frac{dy}{dt})^2}dt $. (The bounds on the integral come from your bounds).
First you should compute $frac{dx}{dt}$ and $frac{dy}{dt}$.
Then compute $ds$ and you could be able to solve it from there.
answered Apr 30, 2014 at 23:51
$endgroup$
0
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Криволинейные интегралы применяют для вычисления длины дуг кривых, площади замкнутых областей, объемов тел.
Дальше проанализируем ответы к примерам на интегрирование в которых с помощью криволинейного интегралу ІІ рода будем вычислять площадь эллипса, астроиды, лемнискаты.
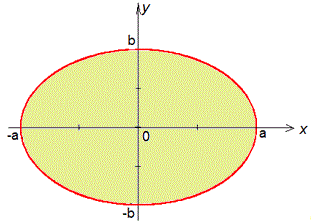
Задание 1 С помощью криволинейного интегралу вычислить площадь, ограниченную эллипсом x=a-cos(t), y=b-sin(t) (0≤φ≤2π).
Решение: Прежде всего нарисуем эллипс, площадь которого нужно найти
Найдем дифференциал координатной функции y=b-sin (t) по переменной t:
dy=b-cos (t) dt.
Вычислим площадь эллипса с помощью криволинейного интеграла:
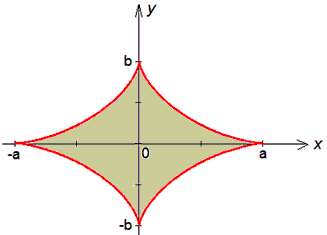
Задание 2 С помощью криволинейного интегралу вычислить площадь астроиды x=a-cos3t, y=b-sin3t (0≤φ≤2π).
Решение: В декартовой системе координат астроида имеет вид
Имеем готовое параметризующее уравнение астроиды, поэтому переходим к нахождению дифференциалу функции y=b-sin3t по переменной t:
dy=3b-sin2(t)-cos(t)dt.
Вычислим площадь эллипса с помощью криволинейного интеграла 2 рода:
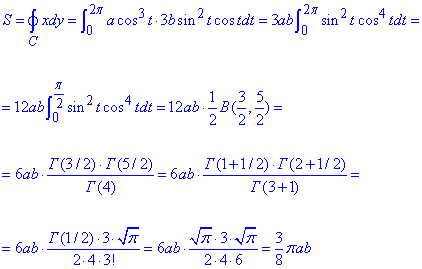
При интегрировании получили специальный интеграл Эйлера, которые расписаны через бета и гамма функции.
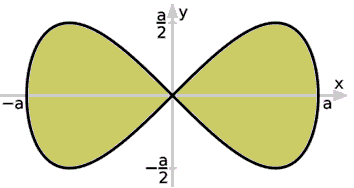
Пример 3. С помощью криволинейного интегралу вычислить площадь лемнискаты (x2+y2)2=a2(x2-y2).
Решение: В прямоугольных координатах лемниската имеет вид двух капелек симметрично расположенных относительно оси Oy.
Сведем заданную кривую (лемнискату) к параметрическому виду с помощью тригонометрической подстановки y=x-tg(φ):
«Игрек» при этом примет значение
После всех превращений можем выписать конечную параметризацию (это половина лемнискаты) :
где -π/4≤φ≤π/4.
Найдем дифференциал от функции 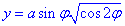
Окончательно дифференциал dy равен
Площадь эллипса найдем через криволинейный интеграл второго рода :
Здесь нашли площадь одного лепесток лемнискаты, а результат умножили на 2.
Если хотите получше понять интегрирование — то проанализируйте вычисление интегралов.
Подобных заданий на нахождение площади плоских фигур через криволинейный интеграл можно навести огромное количество. Рассмотренные фигуры наиболее распространены на практике.
Кроме этого Вы и так видите, что вычисления в основном заключаются:
в параметризации уравнений, если они сложны;
дальше определяем дифференциал и находим криволинейный интеграл.