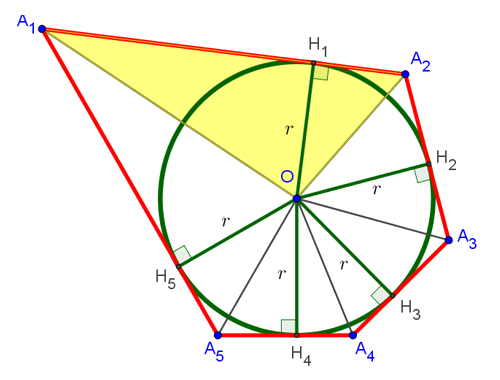
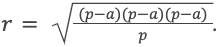Формулы площади круга вписанного и описанного в треугольник и квадрат.
Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
1. Площадь круга
Где S — площадь круга, R — радиус круга.
2. Площадь круга вписанного в квадрат.
Где a/2 — радиус круга, a — длина стороны квадрата.
3. Площадь круга описанного около квадрата.
Где a — длина стороны квадрата.
В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.
4. Площадь круга вписанного в треугольник.
Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)
Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.
Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²
5. Площадь круга описанного около треугольника.
Используя формулу радиуса описанной окружности
R = a/(2*sin(A))
Где a, A — сторона и противолежащий угол соответственно.
Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²
6. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.
Как найти площадь вписанной окружности
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Площадь круга, вписанного в равносторонний треугольник: решение
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
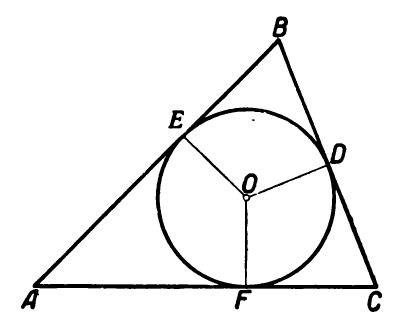
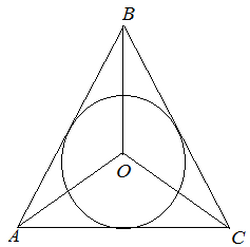
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
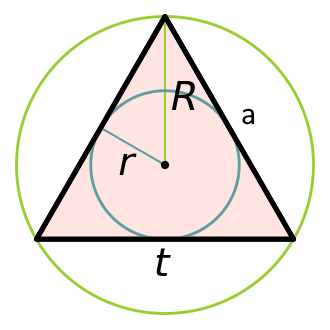
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .
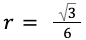
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
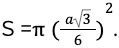
В задачах могут давать длину сторон, тогда
Выражение 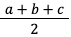
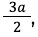
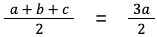
Зная это, формула записывается в виде: S = r * p.
Задачи
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
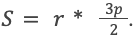
Известно, что он определяется по формуле:
После преобразований выражение упрощается до 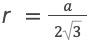
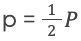
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь круга, вписанного в равносторонний треугольник: решение
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .
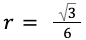
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
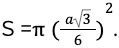
В задачах могут давать длину сторон, тогда 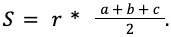
Выражение 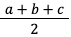
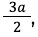
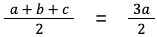
Зная это, формула записывается в виде: S = r * p.
Задачи
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
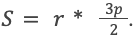
Известно, что он определяется по формуле:
После преобразований выражение упрощается до 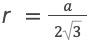
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
http://b4.cooksy.ru/articles/kak-nayti-ploschad-vpisannoy-okruzhnosti
http://bingoschool.ru/manual/ploshhad-kruga-vpisannogo-v-ravnostoronnij-treugolnik-reshenie/
Как найти площадь вписанного четырехугольника?

Площадь вписанного четырёхугольника может быть найдена по формуле Брахмагупты:
где p — полупериметр четырёхугольника, то есть
(формулу Герона можно рассматривать как частный случай этой формулы при d=0).
II способ.

Из треугольника ABC по теореме косинусов
Аналогично, из треугольника ADC
Так как четырехугольник ABCD вписан в окружность,
Так как cos(180º-α)= — cosα
Отсюда,
Приравниваем правы части равенств для AC²
Отсюда,
Найдём синус этого угла, используя основное тригонометрическое тождество
(для 0º<α<180º sinα>0)
и по формуле
найдём
Аналогично,
(так как их сумма равна 180º, а sin(180º-α )=sinα).
В частных случаях: если в окружность вписан правильный четырёхугольник (то есть квадрат), прямоугольник либо четырёхугольник, диагонали которого взаимно перпендикулярны — решение задачи может быть упрощено.
Площадь любого четырёхугольника, в том числе, и вписанного, равна половине произведения его диагоналей на синус угла между ними:
В следующий раз рассмотрим конкретные примеры нахождения площади вписанного четырёхугольника.
В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.
Формула площади многоугольника через радиус вписанной окружности
Нарисуем многоугольник A1A2A3A4A5, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:
Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».
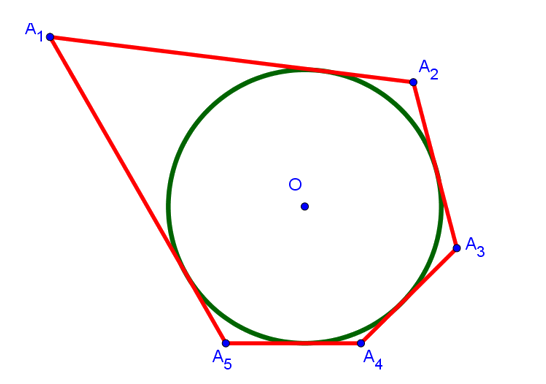
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH1, OH2, OH3, OH4 и OH5), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:
Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:
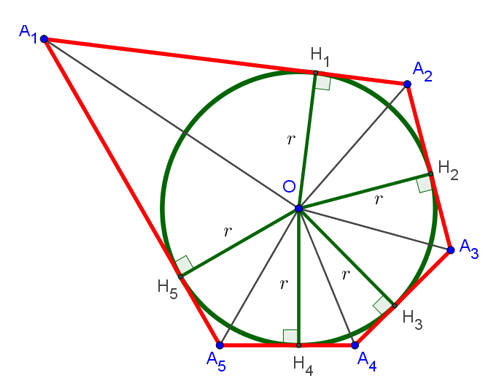
Рассмотрим, чему равна площадь треугольника . На рисунке снизу он выделен жёлтым цветом:
Она равна половине произведения основания A1A2 на высоту OH1, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
Видно, что во всех слагаемых этой суммы ест общий множитель , который можно вынести за скобки. В результате получится вот такое выражение:
То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.
Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
|
Площадь вписанного четырехугольника равна? Формула площади вписанного четырехугольника? Площадь четырехугольника, вписанного в окружность? Вроде бы- согласно правилам- центры окружностей, как вписанных, так и описанных, в квадрат и вокруг него, находятся на пересечении его дигоналей,это упрощает нахождение площади, так как, радиус окружности, описанной вокруг квадрата, равен половине диагонали, отсюда- сторона квадрата = радиус* на корень кв. из 2- х, а площадь- стороне, возведенной во вторую степень. Речь о квадрате, потому что другой четырехугольник не впишется, а опишется вокруг окружности, еще и ромб. система выбрала этот ответ лучшим Эта задача в сформулированном виде имеет смысл только в том случае, если вписанный четырехугольник — это квадрат. В таком случае пусть радиус окружности равен r, а сторона квадрата равна а. Диаметр окружности (он же — диагональ квадрата) равен 2r. По теореме Пифагора а2 + а2 = (2r)2, 2а2 = 4r2 и получаем, что площадь квадрата равна а2 = 2r2. Если же вписанный четырехугольник — не квадрат, то для определения его площади необходимы дополнительные данные. Например, если четырехугольник прямоугольный, то достаточно дать длину, например, меньшей его стороны. Потому что площадь вписанного прямоугольника будет стремиться у нулю при уменьшении длины этой меньшей стороны. Если четырехугольник произвольный, то тем более необходимы для решения задачи какие-то дополнительные данные. Например, стороны или углы этого четырехугольника. Предполагается во всех случаях, что известен радиус окружности. Есть другой вариант — от площади окружности отнять четыре сегмента круга.. Сегмент круга — это разность площади сектора и двух прямоугольных треугольников, опирающихся на него или разница между сектором и прямоугольным треугольником.. a-длина хорды r-радиус b-высота, опущенная на хорду.. S1=a*b/2=a*sqrt(r^2-a^2/4)/2 S2=п*r^2(alpha)/360 alpha=2*arcsin(a*r/2) Итого получится: S=п*r^2(1-E(п*r^2(2*arcsin(ai*r/2))/360-ai*sqrt(r^2-ai^2/4)/2), где Е-знак суммирования сигма по всем четырём ai, которые являются хордами и одновременно сторонами вписанного четырёхугольника.. Проще всего посчитать площадь вписанного четырёхугольника — это провести диагональ между двумя любыми углами, а затем из других углов опустить высоты.. Если длины высот обозначить как a и d, отрезки, отсекаемые от диагонали — b и c, то из рассмотрения четырёх прямоугольных треугольников получаем: S= (a*b+a*c+b*d+d*c)/2 Вот такая простая и очевидная формула, ведь в задании не было указано, что нужно определить через радиус окружности.. Михаил Алексеевич — гражданин РФ 6 лет назад Если четырех угольник это квадрат, то делим квадрат на 4 прямоугольных треугольника, соответственно сторона треугольника равна радиусу, а площадь R*R/2, соответственно площадь 4 треугольников 4R*R/2 или 2R*R или 2R квадрат. В остальных случаях необходимы дополнительные параметры и общей формулы нет, площадь может изменяться от 0 если одна сторона =диаметру а вторая 0 до площади квадрата, формула приведена выше. Galina7v7 6 лет назад Существует несколько сложная формула вычисления площади ПРОИЗВОЛЬНОГО четырёхугольника, но вписанного в окружность : s = корень из(p *(p-a)*(p-b)*(p-c)*(p-d), где p — полупериметр сторон четырёхугольника, a , b , c , d — стороны четырёхугольника. Формула очень напоминает формулу Герона. Ещё есть формула вычисления площади опять таки произвольного четырёхугольника, но по значениям диагоналей 4-х угольника. Знаете ответ? |