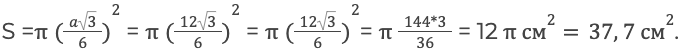Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
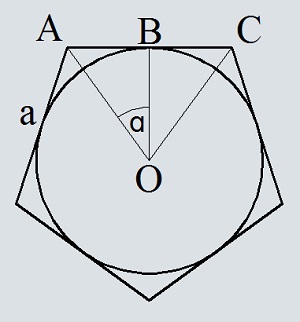
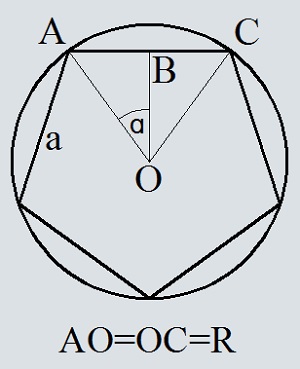
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
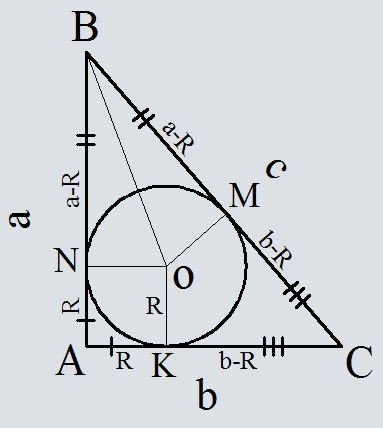
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
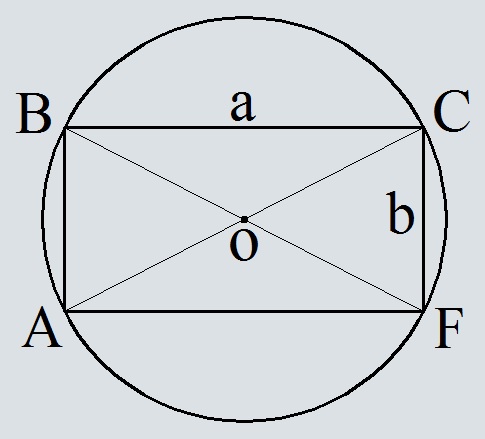
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
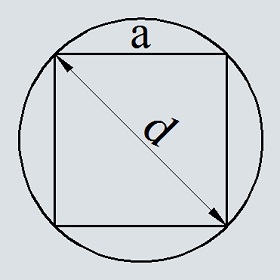
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
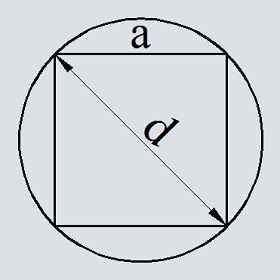
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
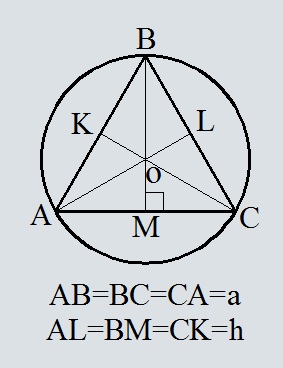
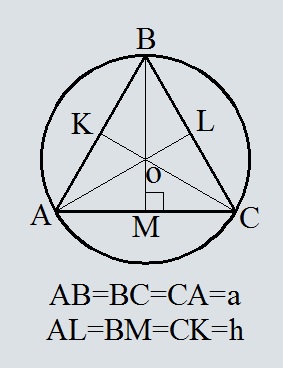
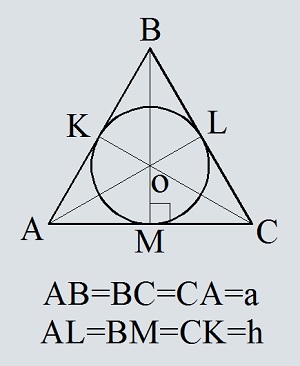
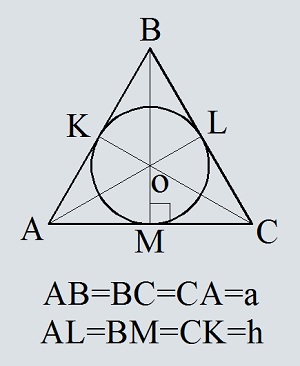
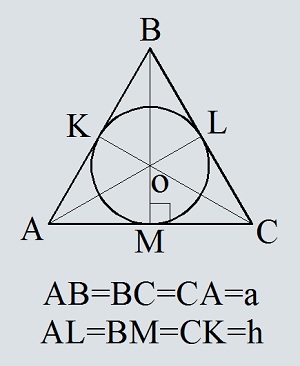
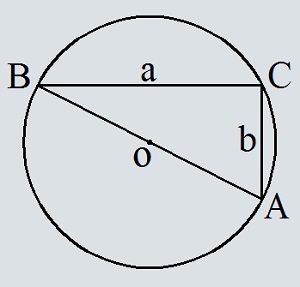
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
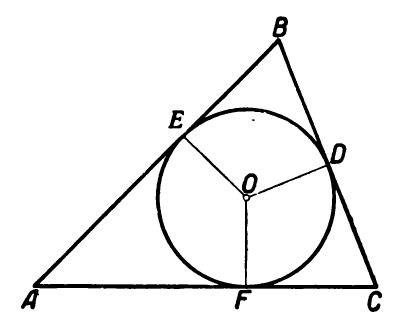
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
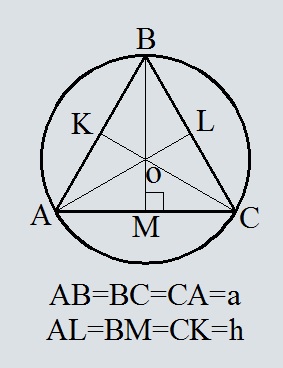
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
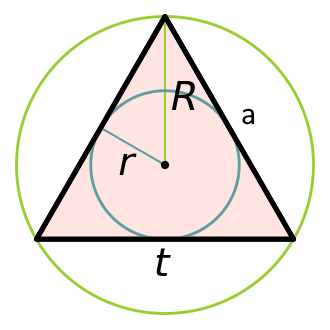
Формулы площади круга вписанного и описанного в треугольник и квадрат.
Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
1. Площадь круга
Где S — площадь круга, R — радиус круга.
2. Площадь круга вписанного в квадрат.
Где a/2 — радиус круга, a — длина стороны квадрата.
3. Площадь круга описанного около квадрата.
Где a — длина стороны квадрата.
В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.
4. Площадь круга вписанного в треугольник.
Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)
Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.
Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²
5. Площадь круга описанного около треугольника.
Используя формулу радиуса описанной окружности
R = a/(2*sin(A))
Где a, A — сторона и противолежащий угол соответственно.
Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²
6. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.
Как найти площадь вписанной окружности
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Площадь круга, вписанного в равносторонний треугольник: решение
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .
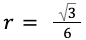
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
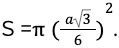
В задачах могут давать длину сторон, тогда
Выражение 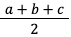
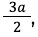
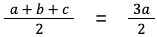
Зная это, формула записывается в виде: S = r * p.
Задачи
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
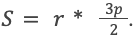
Известно, что он определяется по формуле:
После преобразований выражение упрощается до 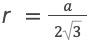
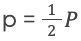
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь круга, вписанного в равносторонний треугольник: решение
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .
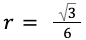
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
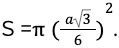
В задачах могут давать длину сторон, тогда 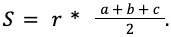
Выражение 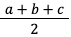
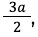
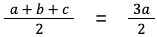
Зная это, формула записывается в виде: S = r * p.
Задачи
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
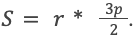
Известно, что он определяется по формуле:
После преобразований выражение упрощается до 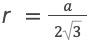
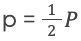
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
http://b4.cooksy.ru/articles/kak-nayti-ploschad-vpisannoy-okruzhnosti
http://bingoschool.ru/manual/ploshhad-kruga-vpisannogo-v-ravnostoronnij-treugolnik-reshenie/
- Площадь круга по радиусу
- Площадь круга по диаметру
- Площадь круга по длине окружности
- Площадь круга по стороне квадрата вписанного в этот круг
- Площадь круга по площади квадрата вписанного в этот круг
- Площадь круга описанного около равностороннего треугольника, по стороне треугольника
- Площадь круга описанного около равностороннего треугольника, по высоте треугольника
- Площадь круга описанного около равностороннего треугольника, по площади треугольника
- Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
- Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
- Площадь круга вписанного в равносторонний треугольник, по площади треугольника
- Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
- Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
- Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
- Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
- Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Площадь круга по радиусу
Формула площади круга по радиусу
S=πR2
Где S — площадь круга,
R — радиус круга,
π=3.14
Площадь круга по диаметру
Формула площади круга по диаметру
Где S — площадь круга,
d — диаметр круга,
π=3.14
Площадь круга по длине окружности
Введите длину окружности c
Формула площади круга по длине окружности
Где S — площадь круга,
c — длина окружности,
π=3.14
Площадь круга по стороне квадрата вписанного в этот круг
Введите сторону квадрата a
Формула площади круга по стороне квадрата вписанного в этот круг
Где S — площадь круга,
a — сторона квадрата,
π=3.14
Площадь круга по площади квадрата вписанного в этот круг
Введите площадь квадрата Sкв
Формула площади круга по площади квадрата вписанного в этот круг
Где Sкр — площадь круга,
Sкв — площадь квадрата,
π=3.14
Площадь круга описанного около равностороннего треугольника, по стороне треугольника
Введите сторону равностороннего треугольника a
Формула площади круга описанного около равностороннего треугольника, по стороне треугольника
Где S — площадь круга,
a — сторона треугольника,
π=3.14
Площадь круга описанного около равностороннего треугольника, по высоте треугольника
Введите высоту равностороннего треугольника h
Формула площади круга описанного около равностороннего треугольника, по высоте треугольника
Где S — площадь круга,
h — высота треугольника,
π=3.14
Площадь круга описанного около равностороннего треугольника, по площади треугольника
Введите площадь равностороннего треугольника Sтр
Формула площади круга описанного около равностороннего треугольника, по площади треугольника
Где Sкр — площадь круга,
Sтр — площадь треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по стороне треугольника
Введите сторону равностороннего треугольника a
Формула площади круга вписанного в равносторонний треугольник, по стороне треугольника
Где S — площадь круга,
a — сторона треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по высоте треугольника
Введите высоту равностороннего треугольника h
Формула площади круга вписанного в равносторонний треугольник, по высоте треугольника
Где S — площадь круга,
h — высота треугольника,
π=3.14
Площадь круга вписанного в равносторонний треугольник, по площади треугольника
Введите площадь равностороннего треугольника Sтр
Формула площади круга вписанного в равносторонний треугольник, по площади треугольника
Где Sкр — площадь круга,
Sтр — площадь треугольника,
π=3.14
Площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Введите количество вершин многоугольника n
Введите длину стороны многоугольника a
Формула площади круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника
Где a — сторона многоугольника,
n — количество вершин многоугольника,
π=3.14
Площадь круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Введите количество вершин многоугольника n
Введите длину стороны многоугольника a
Формула площади круга описанного около правильного многоугольника, по стороне и количеству вершин многоугольника
Где a — сторона многоугольника,
n — количество вершин многоугольника,
π=3.14
Площадь круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Введите сторону a
Введите сторону b
Формула площади круга описанного около прямоугольника, вычисленная по сторонам прямоугольника
Где a, b — стороны прямоугольника,
π=3.14
Площадь круга вписанного в прямоугольный треугольник, по катетам треугольника
Введите катет a
Введите катет b
Формула площади круга вписанного в прямоугольный треугольник, по катетам треугольника
Где a, b — катеты прямоугольного треугольника,
π=3.14
Площадь круга описанного около прямоугольного треугольника, по катетам треугольника
Введите катет a
Введите катет b
Формула площади круга вписанного в равносторонний треугольник, по площади треугольника
Где a, b — катеты прямоугольного треугольника,
π=3.14
Как найти площадь вписанной окружности
Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры — стороны, высоту, диагонали, периметр.

Инструкция
Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
где r — радиус окружности,
π — число «Пи» — математическая постоянная, равная 3,14.
Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.
В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
где r — радиус вписанной окружности,
s∆ — площадь треугольника,
p∆ — полупериметр треугольника.
Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
S = π*(s∆/p∆)².
Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.
В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а — сторона ромба.
Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h — высота трапеции.
Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².
Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
На чтение 5 мин Просмотров 2.6к. Опубликовано 17 мая, 2021
Окружность — одна из самых совершенных фигур в геометрии. Построить ее очень просто — нужен только циркуль. Но при своем совершенстве окружность создает одну из самых сложных проблем — определение площади круга. Почему это является проблемой? Дело в том, что площадь измеряется в квадратных единицах (метрах, дециметрах, миллиметрах…). Но превратить круг в прямоугольник или квадрат практически невозможно. Задача эта беспокоила умы математиков и философов на протяжении тысячелетий и даже получала собственное название — квадратура круга.
Чтобы разобраться в проблеме нужно разделить понятия окружности и круга. Окружность — это замкнутая линия, все точки которой находятся на одинаковом расстоянии от центра. А круг — это часть плоскости, ограниченная этой окружностью. Для окружности мы ищем длину, а для круга — площадь. Какую бы часть круга, ограниченную окружностью, мы не выбрали, одна из сторон обязательно будет криволинейной. Это усложняет расчет площади, если не использовать интегрального исчисления.
Приблизительно, с высокой долей точности можно найти площадь окружности через диаметр по формуле:
Это самая простая формула, позволяющая найти площадь круга, когда известный радиус. Но может возникнуть вопрос, почему найденная площадь будет неточной? Сложность связана с числом π — это отношение длины окружности к диаметру, не имеющая конечного значения. Такие числа называют иррациональными. Еще в 1761 году Иоганн Ламберт доказал, что эта постоянная трансцендентная, то есть, если возвести ее в квадрат, все равно получится иррациональное число.
Сложное доказательство этого утверждения создали Феликс Клейн и профессор Линдеманн. Практическое значение этого открытия состоит в том, что любая формула для определения площади круга, где используется число π дает приблизительный результат, то есть, квадратура круга невозможна в принципе. На данный момент известно число «Пи» с точностью до 31, 4 триллиона знаков после запятой. Для вычислений используют значение 3, 14, а для более точных — 3, 1415926.
Содержание
- Способы вычисления площади круга
- Вычисление площади по радиусу
- Как найти площадь круга через длину окружности
- Как вычислить площадь круга, описанного вокруг правильного многоугольника
Способы вычисления площади круга
Для решения повседневных и большинство технических задач вполне достаточно формулы S= π∙ D2/4. Но в геометрии есть свои подходы к решению. Не всегда дано радиус (диаметр), а измерить эту величину можно только косвенным путем при помощи построений описанных и вписанных многоугольников, дополнительных построений и т.д. Рассмотрим наиболее популярные методы, как узнать площадь круга, более подробно. Сразу же оговоримся, способ интегрального исчисления затрагивать не будем, хотя он и наиболее точный. Воспользуемся только геометрическими способами решения.
Вычисление площади по радиусу
S = π∙r2 — формула для вычисления площади круга, если известный радиус. Как видно, это просто запись предыдущего выражения с учетом того, что r = D/2, отсюда r2 = (D/2)2 = D2/4, что и использовано в основной формуле.
Как найти площадь круга через длину окружности
Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:
R=L/2 π; (1)
D=L/ π. (2)
Используя запись 1 в формуле S = π∙r2 получаем:
S = π(L/2 π)2 = L/4 π.
Аналогичный результат получим, используя формулу 2.
Как вычислить площадь круга, описанного вокруг правильного многоугольника
В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:
S=2π⋅a2/2, где а – сторона квадрата.
Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:
S=π⋅a2/3.
Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:
S=π⋅(2⋅h/3)2.
Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:
S=π⋅( a4/4⋅a2−b2)
В случае прямоугольного треугольника, мы используем формулу:
S=π/4⋅(a2+b2).
Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:
S=π⋅( a⋅d⋅c/4⋅√p⋅(p−a)⋅(p−d)⋅(p−c)).
Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:
S=π⋅a2/12 – для равностороннего треугольника;
S=π⋅b2/4⋅(tgα/2)2 — для равнобедренной трапеции;
S=π⋅(а/2)2=π⋅а2/4 — для квадрата.
Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.
Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:
S = π∙r2/2, или
S= π∙ D2/4/2 = S= π∙ D2/8.
Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах. Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний.