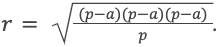Как найти площадь вписанной окружности формула

Формулы площади круга вписанного и описанного в треугольник и квадрат.

Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).

Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов

Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.

Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов

1. Площадь круга

Где S — площадь круга, R — радиус круга.

2. Площадь круга вписанного в квадрат.

Где a/2 — радиус круга, a — длина стороны квадрата.

3. Площадь круга описанного около квадрата.

Где a — длина стороны квадрата.

В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.

4. Площадь круга вписанного в треугольник.

Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)

Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.

Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²

5. Площадь круга описанного около треугольника.

Используя формулу радиуса описанной окружности
R = a/(2*sin(A))

Где a, A — сторона и противолежащий угол соответственно.

Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²

6. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.

Как найти площадь вписанной окружности

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Площадь круга, вписанного в равносторонний треугольник: решение

Содержание:

В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.

Особенности явления

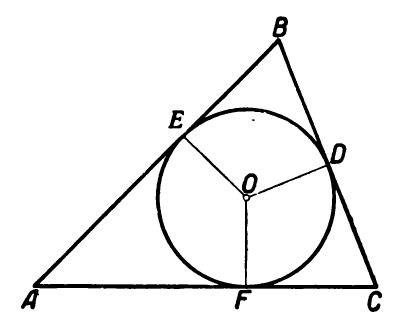
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.

Из вышесказанного следуют свойства:

• В треугольник вписывается лишь один круг.
• Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
• Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.

Способ вычислить площадь круга, вписанного в треугольник

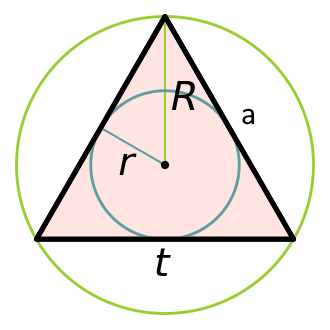
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .

a, где:

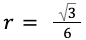
• a – длина стороны геометрической фигуры;
• r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.

После подстановки значения получается выражение для вычисления площади вписанной окружности:

.

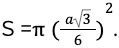
В задачах могут давать длину сторон, тогда
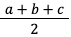
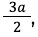
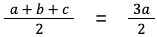
Выражение для равностороннего треугольника можно записать в виде так как 3-угольник равносторонний. С иной стороны – это полупериметр рассматриваемой геометрической фигуры – p.

Зная это, формула записывается в виде: S = r * p.

Задачи

В формулу подставим длину сторон треугольника, после вычислений получим результат.

Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.

Для вычислений необходимо найти радиус r.

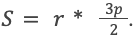
Известно, что он определяется по формуле:

После преобразований выражение упрощается до .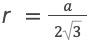

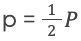
– полупериметр.

Начинаем проводить вычисления.

P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r — радиус круга

D — диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

h — высота треугольника

a — основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

a , b , c , — стороны треугольника

p— полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b — катеты треугольника

Формула площади прямоугольного треугольника, (S):

5. Как вычислить площадь равнобедренного треугольника ?

b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h — высота

Площадь треугольника только через сторону a , (S):

Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

8. Площадь треугольника по стороне и двум углам, формула.

a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

9. Формула расчета площади прямоугольника

b — длина прямоугольника

a — ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

a — сторона квадрата

c — диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d — меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

m — средняя линия

h — высота трапеции

Формула площади трапеции, (S):

2. Формула площади трапеции через диагонали и угол между ними

d ₁, d ₂ — диагонали трапеции

α , β — углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b — верхнее основание

a — нижнее основание

c, d — боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Площадь круга, вписанного в равносторонний треугольник: решение

Содержание:

В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.

Особенности явления

Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.

Из вышесказанного следуют свойства:

• В треугольник вписывается лишь один круг.
• Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
• Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.

Способ вычислить площадь круга, вписанного в треугольник

Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .

a, где:

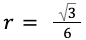
• a – длина стороны геометрической фигуры;
• r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.

После подстановки значения получается выражение для вычисления площади вписанной окружности:

.

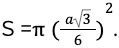
В задачах могут давать длину сторон, тогда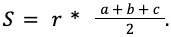
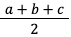
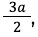
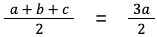
Выражение для равностороннего треугольника можно записать в виде так как 3-угольник равносторонний. С иной стороны – это полупериметр рассматриваемой геометрической фигуры – p.

Зная это, формула записывается в виде: S = r * p.

Задачи

В формулу подставим длину сторон треугольника, после вычислений получим результат.

Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.

Для вычислений необходимо найти радиус r.

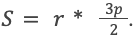
Известно, что он определяется по формуле:

После преобразований выражение упрощается до .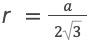

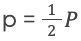
– полупериметр.

Начинаем проводить вычисления.

P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.

Как найти площадь вписанной окружности

Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры — стороны, высоту, диагонали, периметр.

Инструкция

Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
где r — радиус окружности,
π — число «Пи» — математическая постоянная, равная 3,14.

Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.

В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
где r — радиус вписанной окружности,
s∆ — площадь треугольника,
p∆ — полупериметр треугольника.

Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
S = π*(s∆/p∆)².

Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.

В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а — сторона ромба.
Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h — высота трапеции.

Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².

Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

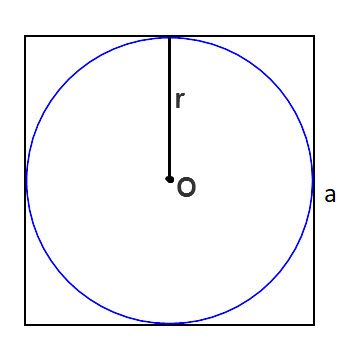
Как найти площадь круга вписанного в квадрат

Вообще мы в прошлый раз определяли площадь круга м², сегодня займёмся площадью круга, который вписан в квадрат! Определим сколько же площадь вписанного круга!

Если мы посмотрим на наш круг вписанный в квадрат, то сразу, наверняка ответили свой вопрос – сколько площадь вписанного круга!?
Если нет, то продолжим…

Формула площади круга вписанного в квадрат

Нам понадобится формула площади круга.

Кроме площади круга у нас есть сторона квадрата, которая обозначена буквой «а». И если посмотреть внимательно на нашу картинку. То мы увидим, что сторона квадрата – это диагональ нашего круга, а мы помним, что диагональ в два раза больше радиуса!
В данном случае

R = а/2

И теперь нам нужно данное равенство занести в формулу и мы получим новую формулу- площадь круга вписанного в квадрат…

S = π(а/2)²

Написать что-нибудь…

площадь круга вписанного в квадрат ,
найти площадь круга вписанного в квадрат ,
площадь квадрата вписанного в круг равна ,
площадь квадрата вписанного в круг ,
площадь квадрата вписанного в круг равна ,
формула площади круга вписанного в квадрат ,

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106). 

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107). 

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны. 

Например, на рисунке 8.106 . 

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны. 

Например, на рисунке 8.107 . 

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике: 

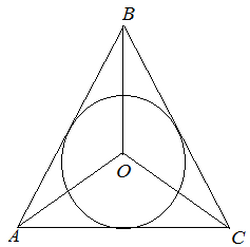
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108); 

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника. 

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают : 

1) для равностороннего треугольника со стороной :

, (8.34)

; (8.35)

2) для произвольного треугольника со сторонами  и площадью : 

, (8.36)

; (8.37)

3) для прямоугольного треугольника с катетами  и гипотенузой : 

, (8.38)

; (8.39)

4) для квадрата со стороной  и диагональю : 

, (8.40)

; (8.41)

5) для прямоугольника с диагональю : 

; (8.42)

6) для ромба с высотой : 

; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность: 

. (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами  и площадью , по формуле  найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

для правильного шестиугольника со стороной : 

, (8.45)

. (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка  является центром вписанной в него и описанной около него окружностей. 

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса  находят по формуле 8.32, а площадь квадрата со стороной  находят по формуле , то согласно условию задачи запишем: , .

А так как , то , , , , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника. 

Решение. Площадь прямоугольника со смежными сторонами  и  находят по формуле .

Пусть , тогда  (рис. 8.118).

Получим: , , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8. 

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

, , .

По формуле 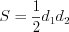 найдем площадь ромба: .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной  находят по формуле: .

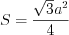
Зная площадь треугольника, найдем его сторону: , , . 

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: .

По формуле 8.30 найдем длину окружности: .

Ответ: .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник. 

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой  находят по формуле 8.38. Тогда . 

Так как треугольник равнобедренный, то его катеты  и  раны и по теореме Пифагора , откуда , . 

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае , .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка  является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат  со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных  и .

Тогда по теореме Пифагора  или , откуда , .

Найдем катет : .

Найдем площадь треугольника: , .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: , откуда . 

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона  найдем площадь треугольника. Так как , то .

Тогда .

Ответ:  .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции. 

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 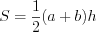 найдем площадь трапеции: .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию  (рис. 8.123) и проведем диагональ трапеции .

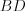
Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

, .

Зная, что  и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то , откуда . Тогда , .

Поскольку четырехугольник  является прямоугольником, то , тогда .

Согласно теореме Пифагора запишем:

, ;

, .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

.

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: . 

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то . 

Площадь круга находят по формуле 8.32. Тогда , а .

Найдем площадь кольца: , .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции. 

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса  находят по формуле: 

. (8.30)

Площадь круга радиуса  находят по формуле: 

. (8.32)