Как найти площадь вписанной окружности около шестиугольника

Ответ:

75π см².

Объяснение:

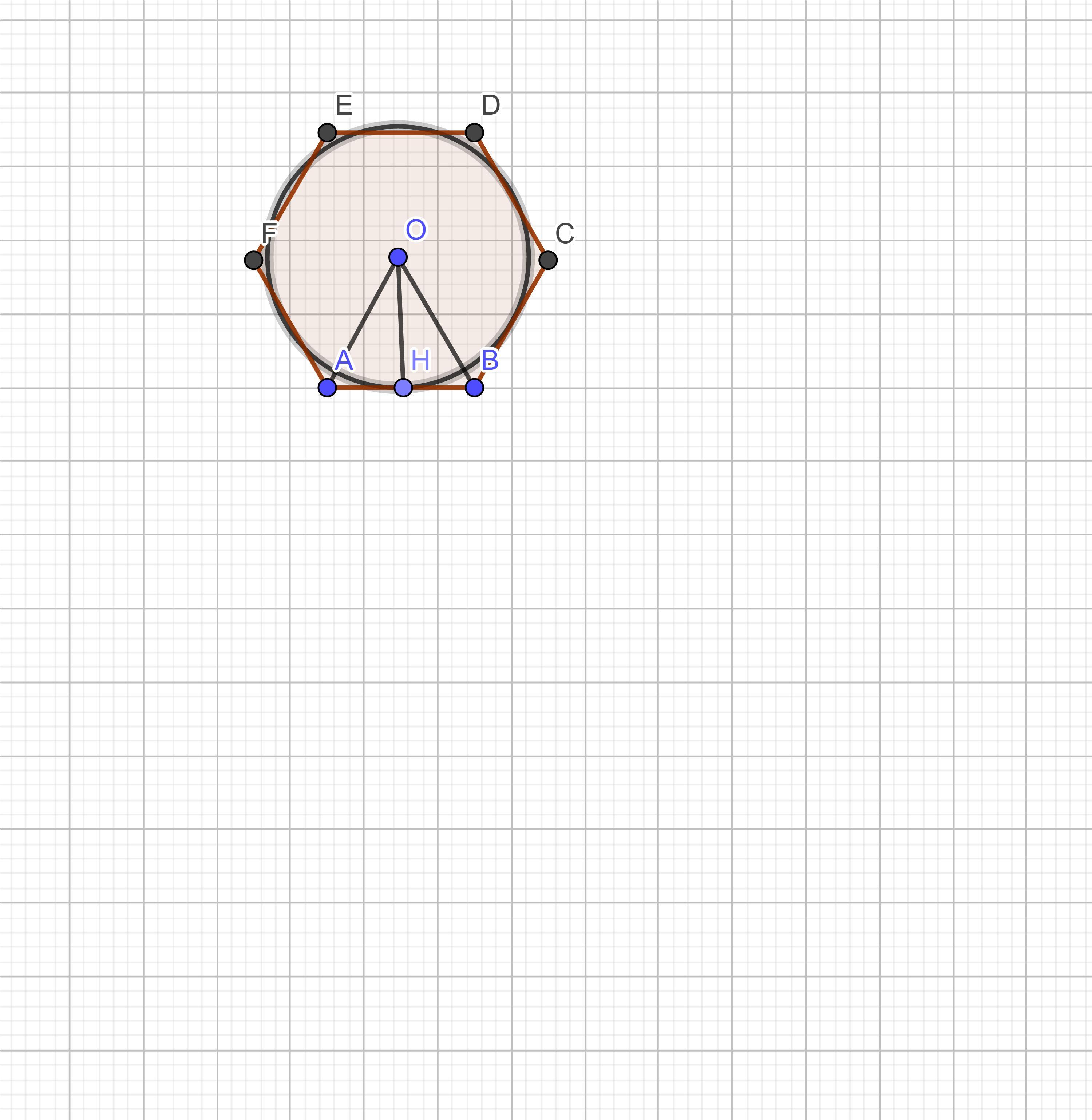
ABCDEF — правильный шестиугольник  со стороной 10 см.

Рассмотрим Δ AOB —  равносторонний , AO=BO=AB= 10 см.

OH — радиус вписанной окружности и высота Δ AOB. Высота равностороннего треугольника определяется по формуле:

h= frac{asqrt{3} }{2} , где  a- сторона треугольника. Тогда

h= frac{10sqrt{3} }{2} =5sqrt{3}  см.

Значит радиус окружности, вписанной в данный шестиугольник

r= 5sqrt{3} см.

Площадь круга найдем  по формуле :

S=pi r^{2} ;

S=pi *(5sqrt{3} )^{2} =pi *25*3=75pi см²

Приложения:

Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

    Given a regular Hexagon with side length a, the task is to find the area of the circle inscribed in it, given that, the circle is tangent to each of the six sides.
    Examples: 
     

    Input: a = 4
Output: 37.68

Input: a = 10
Output: 235.5

    Approach: 
    From the figure, it is clear that, we can divide the regular hexagon into 6 identical equilateral triangles. 
    We take one triangle OAB, with O as the centre of the hexagon or circle, & AB as one side of the hexagon. 
    Let M be mid-point of AB, OM would be the perpendicular bisector of AB, angle AOM = 30 deg
    Then in right angled triangle OAM,
     

    tanx = tan30 = 1/√3 
    So, a/2r = 1/√3 
    Therefore, r = a√3/2 
    Area of circle, A =Πr²=Π3a^2/4

    Below is the implementation of the approach: 
     

    C++

    #include <bits/stdc++.h>

    using namespace std;

    float circlearea(float a)

    {

        if (a < 0)

            return -1;

        float A = (3.14 * 3 * pow(a, 2)) / 4;

        return A;

    }

    int main()

    {

        float a = 4;

        cout << circlearea(a) << endl;

        return 0;

    }

    Java

    import java.util.*;

    class solution

    {

    static double circlearea(double a)

    {

        if (a < 0)

        return -1;

        double A = (3.14 * 3 * Math.pow(a,2) ) / 4;

        return A;

    }

    public static void main(String arr[])

    {

        double a = 4;

        System.out.println(circlearea(a));

    }

    }

    Python 3

    def circlearea(a) :

        if a < 0 :

            return -1

        A = (3.14 * 3 * pow(a,2)) / 4

        return A

    if __name__ == "__main__" :

        a = 4

        print(circlearea(a))

    C#

    using System;

    class GFG

    {

    static double circlearea(double a)

    {

        if (a < 0)

        return -1;

        double A = (3.14 * 3 *

                    Math.Pow(a, 2)) / 4;

        return A;

    }

    public static void Main()

    {

        double a = 4;

        Console.WriteLine(circlearea(a));

    }

    }

    PHP

    <?php

    function circlearea($a)

    {

        if ($a < 0)

            return -1;

        $A = (3.14 * 3 * pow($a, 2)) / 4;

        return $A;

    }

    $a = 4;

    echo circlearea($a) . "n";

    Javascript

    <script>

    function circlearea(a) {

        if (a < 0)

            return -1;

        var A = (3.14 * 3 * Math.pow(a, 2)) / 4;

        return A;

    }

    var a = 4;

    document.write(circlearea(a));

    </script>

    Time complexity: O(1)

    Auxiliary Space: O(1)

    Last Updated :
    20 Aug, 2022

    Like Article

    Save Article

    Источник

    Как найти площадь вписанной окружности

    Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры — стороны, высоту, диагонали, периметр.

    Как найти площадь вписанной окружности

    Инструкция

    Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
    где r — радиус окружности,
    π — число «Пи» — математическая постоянная, равная 3,14.

    Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.

    В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
    где r — радиус вписанной окружности,
    s∆ — площадь треугольника,
    p∆ — полупериметр треугольника.

    Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
    S = π*(s∆/p∆)².

    Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
    Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.

    В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а — сторона ромба.
    Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h — высота трапеции.

    Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².

    Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.

    Видео по теме

    Войти на сайт

    или

    Забыли пароль?
    Еще не зарегистрированы?

    This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

    Источник

    Площадь правильного многоугольника

    Онлайн калькулятор — площадь правильного многоугольника

    Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

    Правильный многоугольник так же называют правильным n-угольником, где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

    В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.

    Около любого правильного многоугольника можно описать окружность.

    Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

    Правильный многоугольник

    Формулы, признаки и свойства правильного многоугольника

    Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

    Многоугольники отличаются между собой количеством сторон и углов.

    Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

    Признаки правильного многоугольника

    Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

    a 1 = a 2 = a 3 = … = a n-1 = a n ,

    α 1 = α 2 = α 3 = … = α n-1 = α n

    где a1 … an — длины сторон правильного многоугольника,
    α 1 … α n — внутренние углы между стронами правильного многоугольника.

    Основные свойства правильного многоугольника

    1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
    2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
    3. Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
    4. Сумма всех углов n-угольника равна: 180° · n — 2
    5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
    6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
    7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
    8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

    Формулы правильного n-угольника

    Формулы длины стороны правильного n-угольника

    Формула стороны правильного n-угольника через радиус вписанной окружности

    a = 2 · r · tg 180° n (через градусы),

    a = 2 · r · tg π n (через радианы)

    Формула стороны правильного n-угольника через радиус описанной окружности

    a = 2 · R · sin 180° n (через градусы),

    a = 2 · R · sin π n (через радианы)

    Формулы радиуса вписанной окружности правильного n-угольника

    Формула радиуса вписанной окружности n-угольника через длину стороны

    r = a : 2 · tg 180° n (через градусы),

    r = a : 2 · tg π n (через радианы)

    Формула радиуса описанной окружности правильного n-угольника

    Формула радиуса описанной окружности n-угольника через длину стороны

    R = a : 2 · sin 180° n (через градусы),

    R = a : 2 · sin π n (через радианы)

    Формулы площади правильного n-угольника

    Формула площади n-угольника через длину стороны

    Формула площади n-угольника через радиус вписанной окружности

    Формула площади n-угольника через радиус описанной окружности

    Формула периметра правильного многоугольника

    Формула периметра правильного n-угольника

    Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

    Формула определения угла между сторонами правильного многоугольника

    Формула угла между сторонами правильного n-угольника

    Правильный треугольник

    Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

    Формулы правильного треугольника

    Формула стороны правильного треугольника через радиус вписанной окружности

    Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

    Формула стороны правильного треугольника через радиус описанной окружности

    Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

    Формула площади правильного треугольника через длину стороны

    Формула площади правильного треугольника через радиус вписанной окружности

    Формула площади правильного треугольника через радиус описанной окружности

    Углы между сторонами правильного треугольника

    Правильный четырехугольник

    Правильный четырехугольник — это квадрат.

    Формулы правильного четырехугольника

    Формула стороны правильного четырехугольника через радиус вписанной окружности

    Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

    Формула стороны правильного четырехугольника через радиус описанной окружности

    Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

    Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

    Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

    Формула радиуса описанной окружности правильного четырехугольника через длину стороны

    Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

    Формула площади правильного четырехугольника через длину стороны

    Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

    Формула площади правильного четырехугольника через радиус вписанной окружности

    Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

    Формула площади правильного четырехугольника через радиус описанной окружности

    Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

    Углы между сторонами правильного четырехугольника

    Правильный шестиугольник

    Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

    Формулы правильного шестиугольник

    Формула стороны правильного шестиугольника через радиус вписанной окружности

    Формула стороны правильного шестиугольника через радиус описанной окружности

    Длина стороны правильного шестиугольника равна радиусу описанной окружности.

    Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

    Формула радиуса описанной окружности правильного шестиугольника через длину стороны

    Формула площади правильного шестиугольника через длину стороны

    Формула площади правильного шестиугольника через радиус вписанной окружности

    Формула площади правильного шестиугольника через радиус описанной окружности

    Углы между сторонами правильного шестиугольника

    Правильный восьмиугольник

    Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

    Окружность, вписанная в правильный многоугольник

    На этом занятии мы рассмотрим следующую тему – «Окружность, вписанная в правильный многоугольник». В первую очередь дадим определение правильному многоугольнику. После чего докажем теорему о том, что внутри любого правильного многоугольника можно вписать окружность, и притом только одну. Кроме того, рассмотрим следствия из этой теоремы.

    Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

    источники:

    http://urokmatematiki.ru/reference-information/formuly-po-geometrii/pravilny-mnogougolnik.php

    http://interneturok.ru/lesson/geometry/9-klass/dlina-okruzhnosti-i-ploschad-kruga/okruzhnost-vpisannaya-v-pravilnyy-mnogougolnik

    Источник

    Радиус окружности, описанной около правильного шестиугольника

    Содержание:

    • Что такое окружность, описанная около правильного шестиугольника
    • Как найти радиус, формула
    • Свойства окружности, описанной около шестиугольника
    • Площадь круга, ограниченного описанной окружностью
    • Пример расчета радиуса окружности, описанной около шестиугольника

    Что такое окружность, описанная около правильного шестиугольника

    Правильный шестиугольник — выпуклый шестиугольник, у которого все стороны и углы равны.

    шестиугольник

    Описанная около многоугольника окружность — это окружность, которая содержит все вершины выпуклого многоугольника. Ее центром является точка пересечения срединных перпендикуляров к сторонам многоугольника, обычно её обозначают прописной буквой О.

    центр описанной окружности

    Как найти радиус, формула

    Для расчетов используем формулу радиуса окружности, описанной около правильного многоугольника.

    Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

    Формула 1

    (R=frac a{2sinleft(frac{360^0}{2n}right)})

    где R — радиус описанной окружности правильного многоугольника,

    а — длина стороны многоугольника,

    n — количество сторон (или вершин) многоугольника.

    Подставим в формулу значение n=6. 

    (R=frac a{2sinleft(frac{360^0}{2n}right)}=R=frac a{2sinleft(frac{360^0}{2·6}right)}=frac a{2sinleft(frac{360^0}{12}right)}=frac a{2sin30^0}.)

    Так как (sin30^0=frac12), то (R=frac a{2sin30^0}=frac a{2·frac12}=frac a1). Получаем формулу радиуса окружности, описанной около правильного шестиугольника:

    Формула 2

    R=a

    где R — радиус описанной окружности,

    а — сторона правильного шестиугольника.

    радиус описанной окружности

    Примечание 1

    Эту же формулу модно найти и другим способом. Биссектрисы углов правильного шестиугольника разбивают его на шесть равных равносторонних треугольников. Точка пересечения биссектрис у правильного шестиугольника совпадает с точкой пересечения срединных перпендикуляров и является центром описанной окружности. Расстояние между центром окружности и вершиной шестиугольника равно радиусу описанной окружности и стороне равностороннего треугольника. Этот отрезок также равен стороне шестиугольника.

    шесть равных треугольников

    Свойства окружности, описанной около шестиугольника

    1. У правильного шестиугольника центры вписанной и описанной окружностей совпадают.
    2. Диаметр описанной окружности совпадает с большей диагональю правильного шестиугольника и равен его удвоенной стороне.

    диаметр описанной окружности шестиугольник

    Площадь круга, ограниченного описанной окружностью

    Чтобы вычислить площадь круга, ограниченного описанной окружностью правильного шестиугольника, используем стандартную формулу площади круга.

    Формула 3

    (S=π·r^2)

    где S — площадь круга,

    π — коэффициент, число π,

    r — радиус круга.

    Так как радиус круга равен стороне правильного шестиугольника, около которого описана окружность, получаем формулу:

    Формула 4

    (S=π·а^2)

    где S — площадь круга,

    π — коэффициент, число π,

    а — сторона правильного шестиугольника.

    Пример расчета радиуса окружности, описанной около шестиугольника

    Задача

    Дано: около правильного шестиугольника описана окружность. Меньшая диагональ правильного шестиугольника равна (5sqrt3 см.)

    Найти: радиус описанной окружности.

    Решение: Обозначим сторону правильного шестиугольника как а. Тогда его меньшая диагональ будет (аsqrt3 см). Следовательно, а=5 см. Радиус окружности, описанной около правильного шестиугольника равен его стороне. R=5 см.

    Ответ: 5 см.

    Насколько полезной была для вас статья?

    Рейтинг: 5.00 (Голосов: 1)

    Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

    Текст с ошибкой:

    Расскажите, что не так

    Поиск по содержимому

    Источник

    Понравилась статья? Поделить с друзьями:
  • Как дела найти среднюю скорость
  • Как можно найти ворованный ноутбук
  • Как найти родственников в архивах онлайн бесплатно
  • Как составить локальный нормативный акт образец
  • Как найти имущество по всей россии