Как найти площадь вписанной окружности в многоугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.

Формула площади многоугольника через радиус вписанной окружности

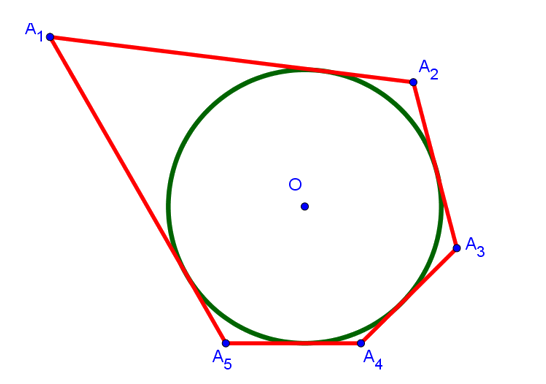
Нарисуем многоугольник A₁A₂A₃A₄A₅, не обязательно правильный, но такой, в который можно вписать окружность. Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника. На рисунке это зелёная окружность с центром в точке O:

Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».

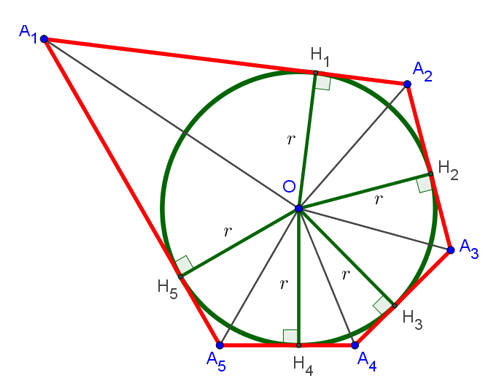
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH₁, OH₂, OH₃, OH₄ и OH₅), которые равны радиусу окружности и перпендикулярны сторонам многоугольника, к которым они проведены. Последнее справедливо, поскольку радиус, проведенный в точку касания, перпендикулярен касательной:

Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:

$[ S = S_{OA_1A_2}+S_{OA_2A_3}+S_{OA_3A_4}+S_{OA_4A_5}+S_{OA_5A_1}. ]$

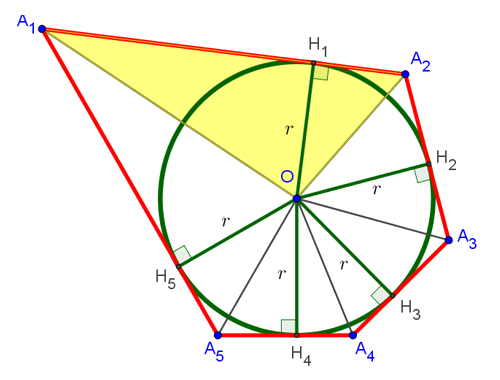
Рассмотрим, чему равна площадь треугольника $S_{OA_1A_2}$ . На рисунке снизу он выделен жёлтым цветом:

Она равна половине произведения основания A₁A₂ на высоту OH₁, проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: $S=frac{1}{2}rcdot A_1A_2$ , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:

$[ S = frac{1}{2}rcdot A_1A_2 + frac{1}{2}rcdot A_2A_3+ ]$

$[ +frac{1}{2}rcdot A_3A_4+frac{1}{2}rcdot A_4A_5+frac{1}{2}rcdot A_5A_1. ]$

Видно, что во всех слагаемых этой суммы ест общий множитель $frac{1}{2}r$ , который можно вынести за скобки. В результате получится вот такое выражение:

$[ S = frac{1}{2}rleft(A_1A_2 +A_2A_3 +A_3A_4 +A_4A_5 +A_5A_1right). ]$

То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P. Чаще всего в этой формуле выражение $frac{1}{2}P$ заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:

То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.

Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.

Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Источник

Как найти площадь вписанной окружности

Площадь окружности, вписанной в многоугольник, можно вычислить не только через параметры самой окружности, но через различные элементы описанной фигуры — стороны, высоту, диагонали, периметр.

Инструкция

Окружность называется вписанной в многоугольник, если имеет общую точку с каждой стороной описанной фигуры. Центр вписанной в многоугольник окружности всегда лежит в точке пересечения биссектрис его внутренних углов. Площадь, ограниченная окружностью, определяется формулой S=π*r²,
где r — радиус окружности,
π — число «Пи» — математическая постоянная, равная 3,14.

Для окружности, вписанной в геометрическую фигуру, радиус равен отрезку от центра до точки касания со стороной фигуры. Следовательно, можно определить зависимость между радиусом вписанной в многоугольник окружности и элементами данной фигуры и выразить площадь окружности через параметры описанного многоугольника.

В любой треугольник возможно вписать единственную окружность с радиусом, определяемым формулой: r=s∆/p∆,
где r — радиус вписанной окружности,
s∆ — площадь треугольника,
p∆ — полупериметр треугольника.

Подставьте полученное значение радиуса, выраженное через элементы описанного около окружности треугольника, в формулу площади окружности. Тогда площадь S окружности, вписанной в треугольник с площадью s∆ и полупериметром p∆ вычисляется по формуле:
S = π*(s∆/p∆)².

Окружность можно вписать в выпуклый четырехугольник при условии, что в нем равны суммы противолежащих сторон.
Площадь S окружности, вписанной в квадрат со стороной a, равна: S= π*a²/4.

В ромбе площадь S вписанной окружности равна: S= π*(d₁d₂/4a)². В этой формуле d₁ и d₂ — диагонали ромба, а — сторона ромба.
Для трапеции площадь S вписанной в нее окружности определяется по формуле: S= π*(h/2)², где h — высота трапеции.

Сторона а правильного шестиугольника равна радиусу вписанной в него окружности, площадь S окружности вычисляется по формуле: S = π*a².

Окружность можно вписать в правильный многоугольник с любым количеством сторон. Общая формула для определения радиуса r окружности, вписанной в многоугольник со стороной а и числом сторон n: r=a/2tg(360°/2n). Площадь S вписанной в такой многоугольник окружности: S=π*(a/2tg(360°/2n)²/2.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Расчёт площади круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника

Калькулятор рассчитывает площадь круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника.

Введите количество вершин многоугольника n

Введите длину стороны многоугольника a

Формула площади круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника

Где a — сторона многоугольника,
n — количество вершин многоугольника,
π=3.14

Вывод формулы площади круга вписанного в правильный многоугольник, по стороне и количеству вершин многоугольника

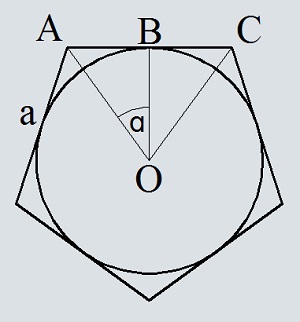
Т.к. треугольник AOC равнобедренный AO=OC. BO будет высотой этого треугольника и равна радиусу окружности BO=R.

Из прямоугольного треугольника ABO зная AB и угол α можем выразить BO.

Подставим полученный радиус в формулу площади окружности

Похожие калькуляторы

Источник

Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.

Содержание

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Площадь круга, описанного около квадрата: формула, примеры решения задач
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Видео: Математика | Вычисление площадей круга и его частей

Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.

Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.

Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.

Формула нахождения площади круга через радиус:

Площадь круга: формула через радиус

Примеры решения заданий по нахождению S-площади круга через R-радиус:

————————————————————————————————————————

Задача: Найдите площадь окружности, если ее радиус равен 7 см.

Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².

Ответ: Площадь окружности равна 153,86 см².

Формула нахождения S-площади круга через D-диаметр:

Площадь круга: формула через диаметр

Примеры решения заданий по нахождению S, если известен D:

————————————————————————————————————————-

Задача: Найдите S круга, если его D равен 10 см.

Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².

Ответ: Площадь плоской круглой фигуры равна 78,5 см².

Нахождение S круга, если известна длина окружности:

Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.

Рассмотрим решение на примере задачи:

———————————————————————————————————————-

Задача: Найдите площадь круга, если известна длина окружности L — 12 см.

Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.

Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².

Ответ: Площадь круга равна 11,46 см².

Площадь круга, вписанного в квадрат: формула, примеры решения задач

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.

Формула нахождения площади круга, вписанного в квадрат:

Площадь круга, вписанного в квадрат: формула

Примеры решения задач по нахождению площади круга, вписанного в квадрат:

———————————————————————————————————————

Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.

Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².

Ответ: Площадь плоской круглой фигуры равна 28,26 см².

————————————————————————————————————————

Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.

Решайте так: Сначала найдем R=a/2=4/2=2 см.

Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².

Ответ: Площадь плоской круглой фигуры равна 12,56 см².

Площадь круга, описанного около квадрата: формула, примеры решения задач

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.

Формула нахождения S круга, описанного около квадратной фигуры:

Площадь круга, описанного около квадрата: формула

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:

Задача

Площадь круга, описанного около квадрата: примеры решения задач

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.

Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².

Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник

Примеры решения заданий:

Задача №1

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры решения задач

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²

Задача №2

Площадь круга, вписанного в равнобедренный треугольник: примеры решения задач

Решение:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.

Задача №3

Площадь круга, вписанного в треугольник: примеры решения задач

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач

Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры решения задач

Вот еще пример решения задачи с использованием формулы Герона.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач

У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.

Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.

Для решения этой задачи нужно использовать такие формулы:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.

Примеры решения задач:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: примеры решения задач

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач

Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: примеры решения задач

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.

Ответ: Радиус равен 6.

В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.

Видео: Математика | Вычисление площадей круга и его частей

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Окружность, вписанная в многоугольник или угол

Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.

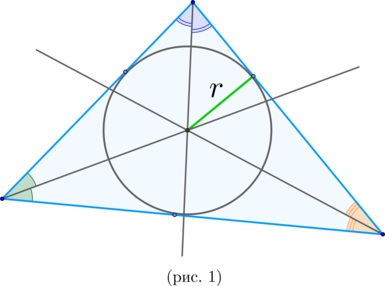
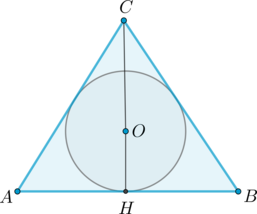
(blacktriangleright) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).

Площадь описанного треугольника ищется по формуле [{Large{S_{triangle}=pcdot r}},]

где (p) – полупериметр.

(blacktriangleright) Если в прямоугольный треугольник вписана окружность, (a, b) – катеты, (c) – гипотенуза, (r) – радиус этой окружности, то верна формула: [{large{r=dfrac{a+b-c}2}}]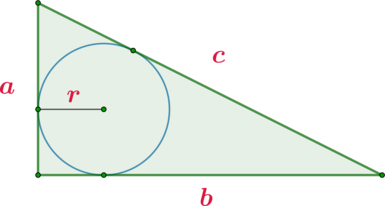

(blacktriangleright) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле

[{large{S_{text{опис.4-к}}=pcdot r}},]

где (p) – полупериметр.

(blacktriangleright) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).

(blacktriangleright) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).

(blacktriangleright) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).

Задание
1

#3106

Уровень задания: Равен ЕГЭ

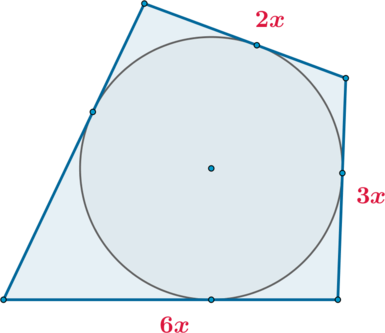
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как (2:3:6). Найдите большую сторону этого четырехугольника, если известно, что его периметр равен (54).

Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны. Следовательно, четвертая сторона равна ((2x+6x)-3x=5x). Тогда можно составить уравнение: [2x+3x+6x+5x=54quadLeftrightarrowquad 6x=20,25] (большая сторона равна (6x))

Ответ: 20,25

Задание
2

#652

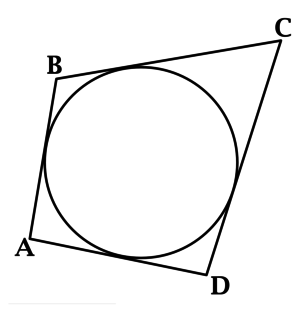
Уровень задания: Равен ЕГЭ

В четырёхугольник (ABCD) вписана окружность, (AB = 3,5), (AD = 4), (BC = 6,5). Найдите длину (CD).

Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны:
(AB + CD = AD + BC), откуда получаем (3,5 + CD = 4 + 6,5), значит, (CD = 7).

Ответ: 7

Задание
3

#2375

Уровень задания: Равен ЕГЭ

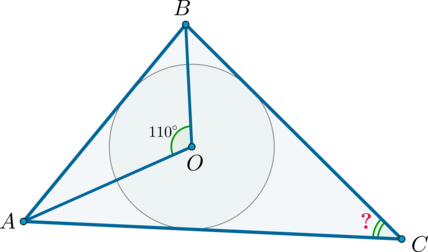
В треугольник (ABC) вписана окружность с центром в точке (O), причем (angle AOB=110^circ). Найдите (angle C) треугольника (ABC). Ответ дайте в градусах.

Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то (AO, BO) – биссектрисы углов (A, B) соответственно.

Следовательно, (angle BAO+angle
ABO=180^circ-110^circ=70^circ).
Также (angle A+angle B=2cdot (angle BAO+angle ABO)=140^circ), следовательно, (angle C=180^circ-(angle A+angle
B)=180^circ-140^circ=40^circ).

Ответ: 40

Задание
4

#3569

Уровень задания: Равен ЕГЭ

Боковые стороны равнобедренного треугольника равны (5), основание равно (6). Найдите радиус вписанной окружности.

Известно, что для любого треугольника (S_{triangle}=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности.
В нашем случае по формуле Герона (полупериметр (p=8)) (S_{triangle}=sqrt{8cdot 3cdot 3cdot 2}=4cdot 3=12). Следовательно, [r=dfrac Sp=dfrac{12}{0,5(5+5+6)}
= 1,5]

Ответ: 1,5

Задание
5

#3560

Уровень задания: Равен ЕГЭ

Около окружности, радиус которой равен (3), описан многоугольник, периметр которого равен (20). Найдите его площадь.

Так как для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности, то [S=dfrac{20}2cdot 3=30]

Ответ: 30

Задание
6

#3561

Уровень задания: Равен ЕГЭ

Сторона правильного треугольника равна (sqrt3). Найдите радиус окружности, вписанной в этот треугольник.

1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также являются высотами и медианами. Пусть (H) – точка касания окружности со стороной (AB) (то есть (OH) – радиус). Следовательно, (OHperp AB) (как часть высоты) и (OH=frac13CH) (как часть медианы, так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины).

Если (AC=2x=sqrt3), то (AH=x), следовательно, (CH=sqrt{4x^2-x^2}=xsqrt3), тогда [OH=dfrac13cdot CH=dfrac13cdot sqrt3cdot dfrac{sqrt3}2=0,5]

2 способ.
Площадь правильного треугольника со стороной (a) равна (S=dfrac{sqrt3}4a^2). Тогда по формуле (S=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности, имеем: [r=dfrac Sp=dfrac{frac{sqrt3}4cdot (sqrt3)^2}{0,5(sqrt3+sqrt3+sqrt3)}
=0,5]

Ответ: 0,5

Задание
7

#3562

Уровень задания: Равен ЕГЭ

Радиус окружности, вписанной в правильный треугольник, равен (dfrac{sqrt3}6). Найдите сторону этого треугольника.

Если (AC=2x), то (AH=x), следовательно, (CH=sqrt{4x^2-x^2}=xsqrt3), тогда [dfrac{sqrt3}6=OH=dfrac13cdot CH=dfrac{sqrt3}3xquadRightarrowquad
x=dfrac12quadRightarrowquad AC=2x=1]

2 способ.
Площадь правильного треугольника со стороной (a) равна (S=dfrac{sqrt3}4a^2). Тогда по формуле (S=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности, имеем: [dfrac{sqrt3}4a^2=dfrac{3a}2cdot rquadRightarrowquad a=2sqrt3r=1]

Ответ: 1

На этапе подготовки к ЕГЭ старшеклассники повторяют базовые определения и формулы, в том числе и по теме «Окружность, вписанная в многоугольник или угол». Достаточно подробное изучение данного раздела планиметрии осуществляется, как правило, в средней школе. В связи с этим необходимость повторения основных формул и понятий по теме «Окружность, вписанная в угол или многоугольник» на этапе подготовки к ЕГЭ возникает у многих выпускников. Поняв принцип решения подобных заданий, старшеклассники смогут рассчитывать на получение достаточно высоких баллов по итогам сдачи единого государственного экзамена.

Готовьтесь к ЕГЭ вместе с образовательным порталом «Школково»

Занимаясь перед прохождением аттестационного испытания, многие старшеклассники сталкиваются с проблемой поиска базовых понятий и формул для нахождения радиуса окружности, вписанной в правильный многоугольник, и других параметров. Далеко не всегда их легко найти в Интернете, как и, например, задачи на правильный шестиугольник. А школьного учебника может просто не оказаться под рукой в нужное время. Для того чтобы ликвидировать пробелы в знаниях по этому и другим математическим разделам, обратитесь к образовательному проекту «Школково». На нашем сайте представлен весь необходимый материал, изложенный доступно и понятно. Какими свойствами обладает окружность, вписанная в угол и многоугольник, и какие формулы необходимо знать для успешного решения задач по данной теме? Ответы на эти и другие вопросы вы найдете на сайте «Школково» в разделе «Теоретическая справка».

Чтобы подготовка к единому госэкзамену была действительно эффективной, рекомендуем также попрактиковаться в решении соответствующих задач. Большая база заданий представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.

УСТАЛ? Просто отдохни

Источник