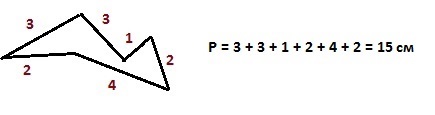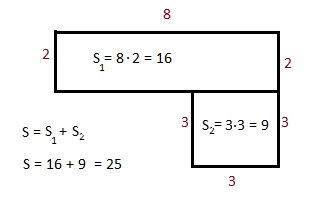Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.
Вот формула для нахождения площади прямоугольника:
S = a · b
В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.
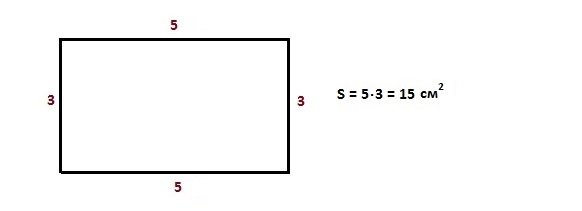
Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.
Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.
Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
3 · 5 =
15 (см2)
Ответ: площадь прямоугольника равна 15 см2.
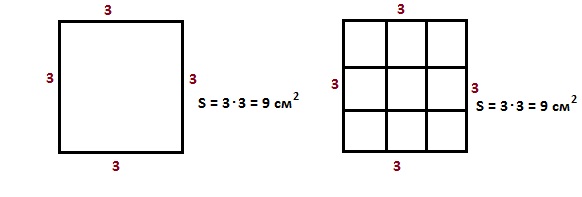
Теперь давайте найдём площадь квадрата со стороной 4 см.
Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.
4 · 4 =
16 (см2)
Ответ: площадь квадрата равна 16 см2.
Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.
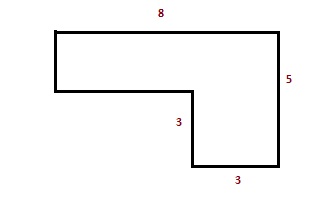
Найдите площадь фигуры, изображённой на рисунке.
Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.
А площади прямоугольников мы легко можем найти с помощью
известной формулы.
Напомним, что противоположные стороны прямоугольника равны.
Итак, стороны первого прямоугольника равны 5 см и 4 см.
5 · 4 =
20 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
Ширина этого прямоугольника равна 2 см.
7 – 4 = 3 (см) – длина второго прямоугольника
3 · 2 = 6
(см2) – площадь второго прямоугольника
Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.
20 + 6 = 26
(см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.
Найдём площадь первого прямоугольника.
Одна его сторона равна 4 см.
5 – 2 = 3 (см) – длина стороны первого прямоугольника
4 · 3 =
12 (см2) – площадь первого прямоугольника
Теперь найдём площадь второго прямоугольника.
7 · 2 =
14 (см2) – площадь второго прямоугольника
12 + 14 =
26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Решим следующую задачу.
Найдём площадь ещё одной фигуры, изображённой на рисунке.
Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.
Получилось 3 прямоугольника.
Найдём площадь первого прямоугольника.
7 · 2 =
14 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
7 – 4 = 3 (см) – длина одной стороны второго прямоугольника
8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника
Получается, что это квадрат, так как длина всех его сторон равна 3
см.
3 · 3 = 9
(см2) – площадь квадрата
И найдём площадь последнего прямоугольника.
Его ширина равна 3 см. Длина равна 7 см.
3 · 7 =
21 (см2) – площадь третьего прямоугольника
Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.
14 + 9 + 21 =
44 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 44 см2
Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:
И решим ещё одну задачу.
Найдите площадь незаштрихованной фигуры.
На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.
9 · 5 =
45 (см2) – площадь большего прямоугольника
5 · 3 =
15 (см2) – площадь меньшего прямоугольника
А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.
45 – 15 =
30 (см2) – площадь незаштрихованной фигуры
Ответ: площадь незаштрихованной фигуры равна 30 см2.
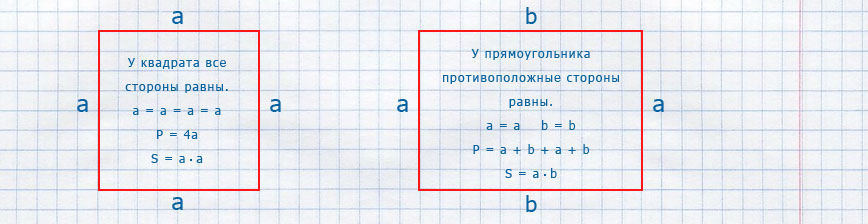
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
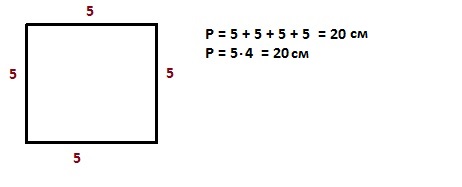
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
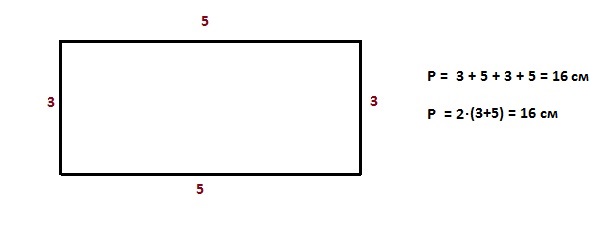
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
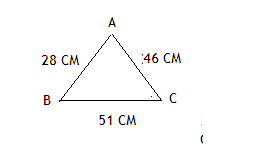
Задача 1
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
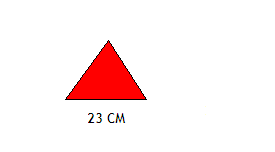
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
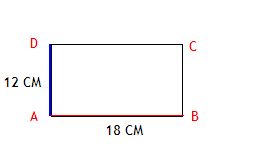
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
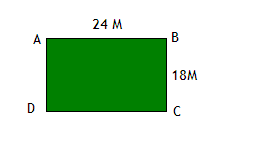
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
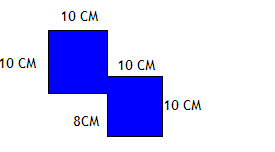
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
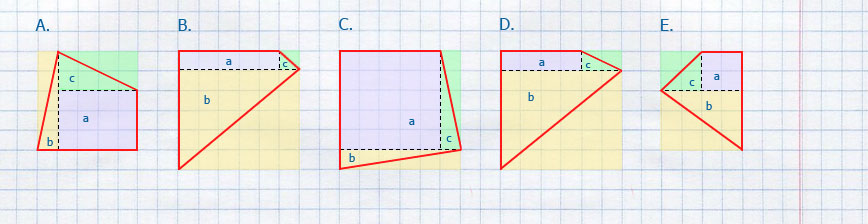
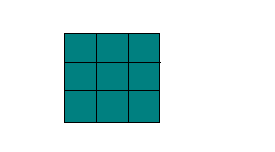
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
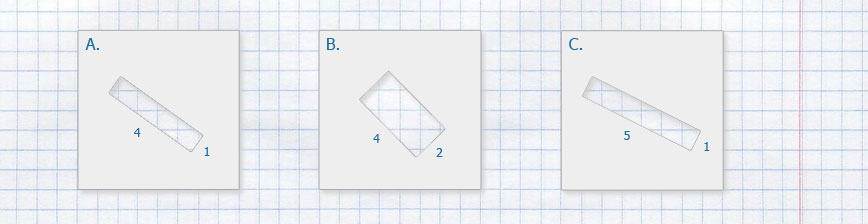
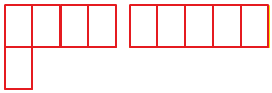
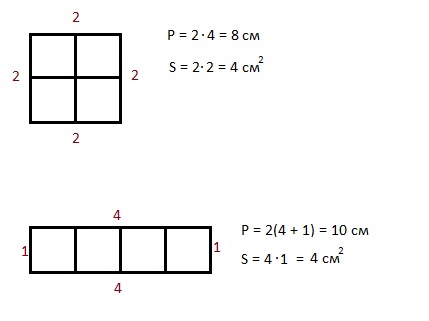
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
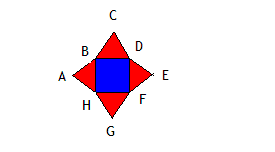
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
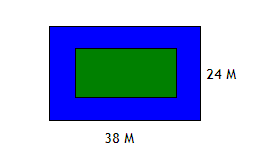
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
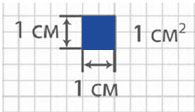
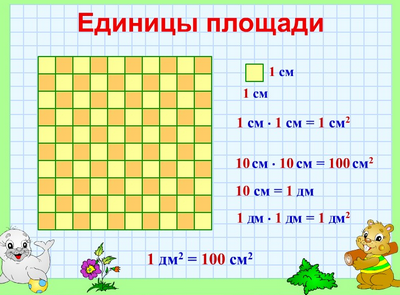
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
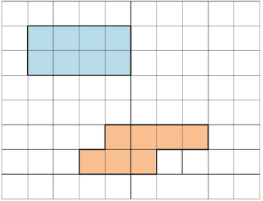
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
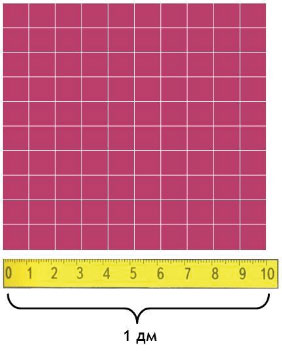
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
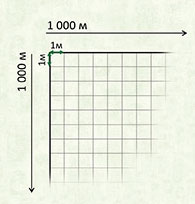
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
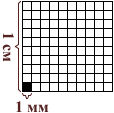
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
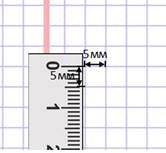
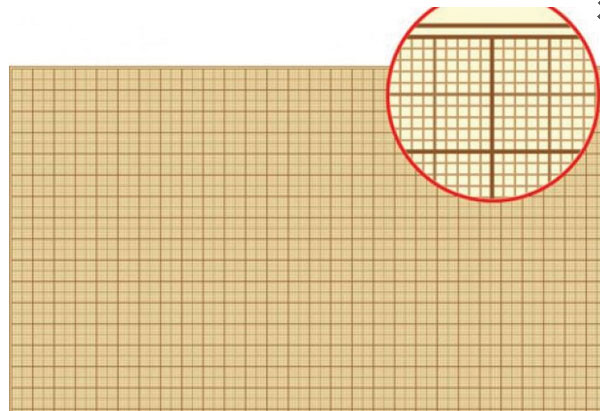
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 40. Урок 16,
Петерсон, Учебник, часть 2
Страница 44. Урок 17,
Петерсон, Учебник, часть 2
Страница 50. Урок 19,
Петерсон, Учебник, часть 2
Страница 58. Урок 23,
Петерсон, Учебник, часть 2
Страница 61. Урок 24,
Петерсон, Учебник, часть 2
Страница 85. Урок 35,
Петерсон, Учебник, часть 2
Страница 88. Урок 37,
Петерсон, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 3
Страница 47. Урок 16,
Петерсон, Учебник, часть 3
Страница 51. Урок 17,
Петерсон, Учебник, часть 3
3 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 1
Страница 84. Урок 30,
Петерсон, Учебник, часть 1
Страница 85. Урок 31,
Петерсон, Учебник, часть 1
Страница 87. Урок 32,
Петерсон, Учебник, часть 1
Страница 51. Урок 23,
Петерсон, Учебник, часть 3
Страница 70. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 27. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 29. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
Периметр прямоугольника – удвоенная сумма длины и высоты — 2∙(a+b)
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
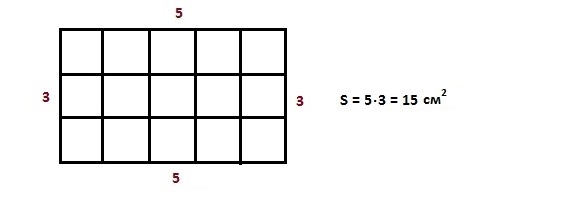
Разделим этот прямоугольник на квадраты
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
СОСТАВНЫЕ ФИГУРЫ
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты
Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
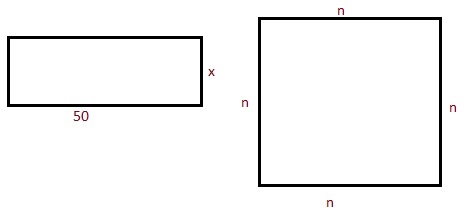
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
1. Вычислим сторону квадрата
4∙n = 80 — периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
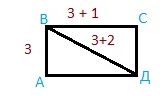
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
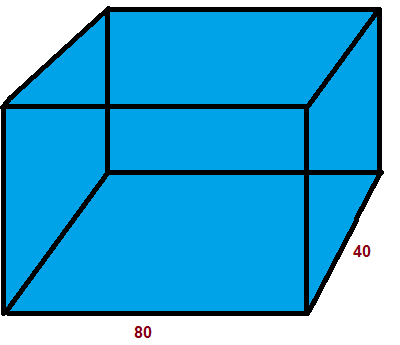
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см