Как найти площадь закрашенной фигуры огэ - Исправление недочетов и поиск решений вместе с Examum.ru

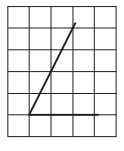
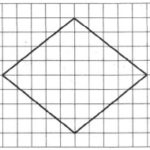
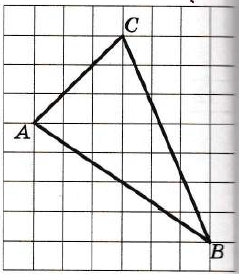
Я позволю себе также нетривиальный метод решения без использования теоремы Пифагора.

Дострою прямоугольник жёлтым цветом ABCD. Как мы видим на моём эскизе его площадь равна произведению клеток длинной стороны на клетки короткой стороны, точнее 4 х 3 = 12 клеток.

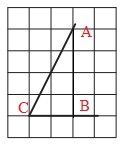
Далее я дострою голубой прямоугольник fBgh недостающего треугольника Bgh он занимает площадь 2 клетки или 1 х 2 = 2, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника, а точнее 1 клетку или 2 : 2 = 1.

Осталось ещё немного. Я дострою малиновый прямоугольник CDeg недостающего треугольника Deg он занимает площадь в 6 клеток или 3 х 2 = 6, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника а точнее 3 клетки или 6 : 2 = 3.

А теперь завершим расчёт:

Я отниму от площади большого прямоугольника ABCD 2 треугольника Bgh и Deg. Решаем:

12 — 1 — 3 = 8.

Мой ответ 8 клеток

Задача решена нетривиальным эксклюзивным методом с использованием не только логического, но и абстрактного мышления. Без квадратов катетов и квадрата гипотенузы.

Источник

Решение заданий №19(задания на
клетчатой бумаге)

1.Основные типы задач

1.
Определение тангенса угла;

2.
Определение площади фигуры (ромба, трапеции,
параллелограмма, треугольника);

3.
Определение расстояния от точки до прямой
(отрезка);

4.
Определение длины средней линии треугольника и
трапеции;

5.
Определение длины большего катета, большей
диагонали;

6.
Определение площади сложных или составных фигур;

7.
Определение градусной меры вписанного угла.

1.Определение
тангенса угла

Задача
1

Найдите
тангенс угла А треугольника ABC, изображённого
на рисунке 1.

Решение:

Ответ: 0,4.

Рис.1

Задача 2

Найдите
тангенс угла AOB, изображённого
на рисунке 3.

Решение:

1. Достроим до прямоугольного треугольника СОВ.

Ответ: 2.

Рис. 3

2. Определение площади фигуры

Задача 1

На
клетчатой бумаге с размером клетки 1×1 изображён параллелограмм (рис. 7).
Найдите его площадь.

Решение:

1. Проведем высоту.

2.
Основание 5

Высота 2

2. Найдем площадь

Ответ: 10.

Рис. 7

Задача 2

На
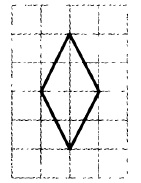
клетчатой бумаге с размером клетки 1×1 изображён ромб (рис. 9).
Найдите площадь этого ромба.

Решение:

1.
Проведем диагонали.

2.
Найдем площадь

Ответ: 30.

Рис. 9

3. Определение расстояния от
точки до прямой (отрезка)

Задача 1

На
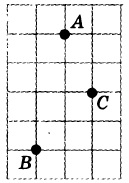
клетчатой бумаге с размером клетки 1×1 отмечены три
точки: A, B и C (рис. 11). Найдите расстояние от
точки A до середины отрезка BC.

Решение:

1. Построим отрезок ВС и

отметим
его середину т.О.

2.
Соединим т.А с т.О. Получа-

ем
нужное расстояние:

Ответ:
8

Рис. 11

4. Определение длины средней линии
треугольника и трапеции

Задача 1

На
клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC
(рис. 14). Найдите длину его средней линии, параллельной стороне AC.

Решение:

Средняя линия

Ответ:
4.

Рис. 14

Задача 2

На
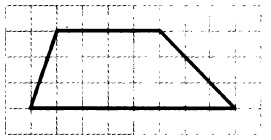
клетчатой бумаге с размером клетки 1×1 изображена трапеция (рис. 15). Найдите
длину её средней линии.

Основания
трапеции соответствен-но равны 7 и 1

Средняя
линия

Ответ:
4.

Рис.15

5. Определение длины большего катета, большей диагонали

Задача 1

На
клетчатой бумаге с размером клетки 1×1 изображён прямоугольный
треугольник (рис. 16). Найдите длину его большего катета.

Решение:

По
рисунку видно, что длина

большего
катета = 6.

Ответ:
6.

Рис. 16

6. Определение площади сложных
или составных фигур

Задача 1

На
клетчатой бумаге с размером клетки 1×1 изображена фигура (рис. 18). Найдите её
площадь.

Решение:

Посчитаем
количество клеток внутри закрашенной области: их 19

Ответ:
19.

Рис. 18

Задача 2

Площадь
одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке
19.

Решение:
1 способ (рис. 19.1)

Найдём
площадь данной фигуры по формуле Пика:

Ответ:
20,5.

Рис. 19

Рис. 19.1

Решение:
2 способ (рис.19.2)

Площадь
данной фигуры

равна
разности площади

квадрата
и двух треугольников:

Ответ:
20,5.

Рис. 19.2

Задачи для самостоятельно решения

I.
Определение
тангенса угла

1. Найдите тангенс угла А треугольника, изображённого на рисунке.

2. Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

3. Найдите тангенс угла AOB,
изображённого на рисунке.

4. Найдите тангенс углаAOB,
изображённого на рисунке.

5. Найдите тангенс углаAOB,
изображённого на рисунке.

6. Найдите тангенс угла AOB, изображённого на рисунке.

7. Найдите
тангенс углаAOB.

8. Найдите тангенс углаAOB.

9. Найдите тангенс угла AOB.

10.
Найдите тангенс угла, изображённого на рисунке.

II.
Определение площади фигуры (ромба, трапеции,
параллелограмма, треугольника)

1. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм.
Найдите его площадь.

2. На клетчатой бумаге с
размером клетки 1х1 изображён треугольник. Найдите его площадь.

3. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник.

4. На клетчатой бумаге с
размером клетки 1х1 изображён ромб. Найдите его площадь.

5. На клетчатой бумаге с
размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

6. На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите её площадь.

7. На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите её площадь.

III.
Определение расстояния от точки до прямой
(отрезка)

1. На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние от точки А до
прямой ВС. Ответ выразите в сантиметрах.

2. На клетчатой бумаге с
размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой ВС.
Ответ выразите в сантиметрах.

3. На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С. Найдите расстояние
от точки А до середины отрезка ВС. Ответ выразите
в сантиметрах.

4. На клетчатой бумаге с
размером клетки 1 см × 1 см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.

5. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены
точки А, В и С. Найдите расстояние
от точки А до прямой BC. Ответ выразите в сантиметрах.

IV.
Определение длины средней линии треугольника
и трапеции

1. На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.

2. На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.

3. На клетчатой бумаге с
размером клетки 1×1 изображён треугольник ABC. Найдите длину
его средней линии, параллельной стороне AC.

4. На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

5. На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

6. На клетчатой бумаге с
размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

V.
Определение длины большего катета, большей
диагонали

1. На клетчатой бумаге с
размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его
большего катета.

2. На клетчатой бумаге с
размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его
большего катета.

3. На клетчатой бумаге с
размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его
большего катета.

4. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину
его большей диагонали.

5. На клетчатой бумаге с
размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

VI.
Определение площади сложных или составных
фигур

1. На клетчатой бумаге с размером
клетки 1х1 изображена фигура. Найдите её площадь.

2. На клетчатой бумаге с
размером клетки 1х1 изображена фигура. Найдите её площадь.

3. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её
площадь.

4. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её
площадь.

5. Площадь одной клетки равна
1. Найдите площадь фигуры, изображённой на рисунке.

6. Площадь одной клетки равна
1. Найдите площадь фигуры, изображённой на рисунке.

VII.
Определение площади сложных или составных
фигур

1. Найдите угол ABC. Ответ дайте в градусах.

2. Найдите угол ABC. Ответ дайте в градусах.

3. Найдите угол ABC. Ответ дайте в градусах.

4. Найдите угол ABC. Ответ дайте в градусах.

5. Найдите угол ABC. Ответ дайте в градусах.

6. Найдите угол ABC. Ответ дайте в градусах.

II. Определение площади
фигуры (ромба, трапеции, параллелограмма, треугольника

III. Определение расстояния от точки до
прямой (отрезка)

IV. Определение расстояния от точки до
прямой (отрезка)

V. Определение длины большего катета,
большей диагонали

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.

Задание OM1901o

На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.

Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1902o

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.

Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее – 4 клеткам. Полусумма оснований:

( 8 + 4 ) / 2 = 6

Ответ: 6

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1903o

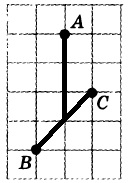
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Проведем необходимые отрезки:

Из рисунка можно вычислить длину – это 3.

Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1904o

Найдите тангенс острого угла, изображённого на рисунке.

Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:

Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.

Согласно определению тангенса, из треугольника ∆АВС можем записать:

tg∠C=AB/BC.

По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):

АВ=4, ВС=2.

Получаем:

tg∠C=4/2=2.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1905o

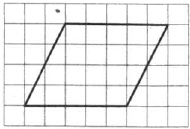
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Площадь параллелограмма вычисляется так:

S=a·h_a

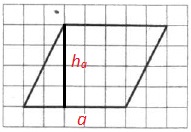
Обозначим a и h_a на рисунке:

Теперь определим их длины по рисунку:

a=5; h_a=4.

Вычисляем искомую площадь:

S=5·4=20.

Ответ: 20

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1906o

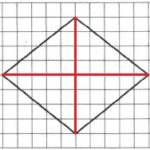
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.

Площадь ромба будем искать через его диагонали:

S=d₁·d₂/2

Линии диагоналей обозначим на рисунке красным:

Обозначим меньшую диагональ через d₁, большую – через d₂ (можно наоборот). Определим их длины из рисунка:

d₁=8; d₂=10.

Находим площадь фигуры:

S=8·10/2=40

Ответ: 40

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 18OM21R

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

: ОГЭ по математике

Вебинар на тему: «Задания по геометрии в ОГЭ-2021 по математике»

Ведущая: Фридман Елена Михайловна

→ презентация к вебинару

Рассмотрены задания из ОГЭ по геометрии:

— Планиметрия. Часть 1 (задания 15 – 18);

— Задание 25 из части 2.

№	Понятия и свойства
15	Треугольник. Медиана, высота, биссектриса, средняя линия, сумма углов, внешний угол, соотношения между сторонами и углами. Теорема косинусов. Четырехугольник. Параллелограмм (ромб, прямоугольник, квадрат), трапеция, их свойства. Признаки параллельности прямых.
16	Вписанные и описанные треугольники и четырехугольники. Касательные, хорды, углы, секущая, угол, образованный касательной и хордой, вписанный угол. Теорема синусов.
17	Площадь треугольника, четырехугольника, решение треугольника.
18	Задачи на клетчатой бумаге, площадь фигуры, центральный и вписанный углы, градусная мера дуги окружности
19	Выбор верного утверждения

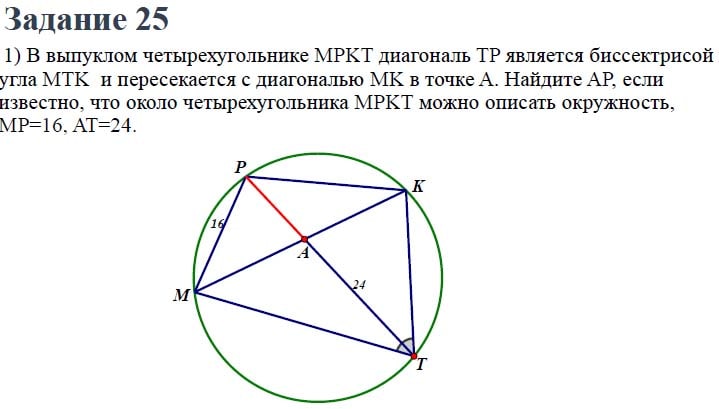
Примеры задач 25:

Связанные страницы:

Решение заданий Варианта №18 из сборника ОГЭ 2022 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.

ЧАСТЬ 1

Задание 1-5.
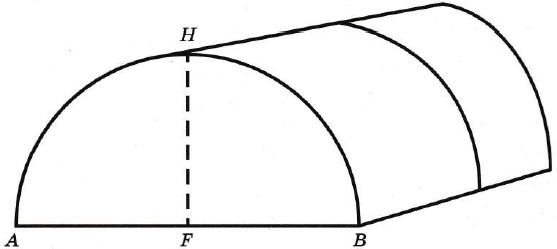
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.

Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы – одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.

Задание 6.
Найдите значение выражения frac{1}{frac{1}{21}+frac{1}{28}}.

Задание 7.
На координатной прямой отмечены числа х, у и z.

Какая из разностей у – z, у – x, x – z отрицательна?

1) у – z
2) у – x
3) x – z
4) ни одна из них

Задание 8.
Найдите значение выражения frac{2^{-6}cdot 2^{6}}{2^{-8}}.

Задание 9.
Решите уравнение х² – 35 = 2х.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 10.
Вероятность того, что новый утюг прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,85. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Задание 11.
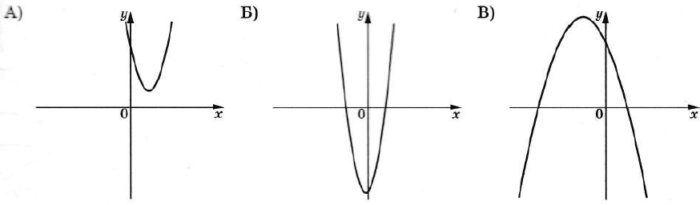
На рисунках изображены графики функций вида у = ах² + bх + c. Установите соответствие между графиками функций и знаками коэффициентов а и с.

ГРАФИКИ

КОЭФФИЦИЕНТЫ

1) а > 0‚ с < 0
2) а < 0, с > 0
3) а > 0, с > 0

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.
Работа постоянного тока (в джоулях) вычисляется по формуле A = I²Rt‚ где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите А (в джоулях), если t = 10 с, I = 4 A и R = 2 Ом.
Ответ задания: 320.

Задание 13.
Укажите решение неравенства

– 3 – x ≤ 4x + 7

1) (–∞; –0,8]
2) [–2; +∞)
3) (–∞; –2)
4) (–0,8; +∞)

Задание 14.
В 8:00 часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В 23:00 того же дня часы отставали на 15 минут. На сколько минут отставали часы спустя 36 часа после того, как они сломались?
Ответ задания: 36.

Задание 15.
В треугольнике АВС угол С равен 90°‚ АС = 14‚ АВ = 20. Найдите sin В.

Задание 16.
В окружности с центром О отрезки АС и BD – диаметры. Угол AOD равен 108°. Найдите угол АСВ. Ответ дайте в градусах.

Задание 17.
Площадь параллелограмма АВСD равна 96. Точка Е – середина стороны АВ. Найдите площадь треугольника СВЕ.

Задание 18.
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.

Задание 19.
Какие из следующих утверждений верны?

1) Если диагонали параллелограмма равны, то он является ромбом.
2) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Решите уравнение х⁴ = (3х – 4)².

Задание 21.
Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Ответ задания: 21.

Задание 22.
Постройте график функции y = x² – 11x – 2|x – 5| + 30 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
Ответ задания: –0,25; 0.

Задание 23.
Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что АВ = 9, ВС = 12, АС = 18, АК = 5, СN = 9. Найдите длину отрезка КN.
Ответ задания: 6.

Задание 24.
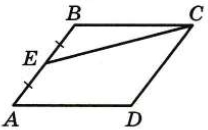
Сторона АD параллелограмма АВСD вдвое больше стороны АВ. Точка G – середина стороны АD. Докажите, что BG – биссектриса угла АBС.

Задание 25.
В трапеции АВСD основания АD и ВС равны соответственно 34 и 2, а сумма углов при основании АD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой СD, если АВ = 24.
Ответ задания: 13,5.

Источник варианта: Сборник ОГЭ 2022 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.7 / 5. Количество оценок: 3

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Слайд 2

Текст слайда:

Задания:

Демо-версия!

Слайд 3

Текст слайда:

№1

Найдите синус угла АОВ. В ответе укажите
значение синуса, умноженное на

Ответ

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

1. Вспомнить что называют синусом острого угла прямоугольного треугольника.

2. Записать формулу нахождения sinО.

Построение:

Слайд 4

Текст слайда:

№2

KarMaN01@yandex.ru

Информация

Слайд 5

Текст слайда:

№3

KarMaN01@yandex.ru

Информация

Слайд 6

Текст слайда:

№4

KarMaN01@yandex.ru

Информация

Слайд 7

Текст слайда:

№5

KarMaN01@yandex.ru

Информация

Слайд 8

Текст слайда:

№6

KarMaN01@yandex.ru

Информация

Слайд 9

Текст слайда:

№7

KarMaN01@yandex.ru

Информация

Слайд 10

Текст слайда:

№8

KarMaN01@yandex.ru

Информация

Слайд 11

Текст слайда:

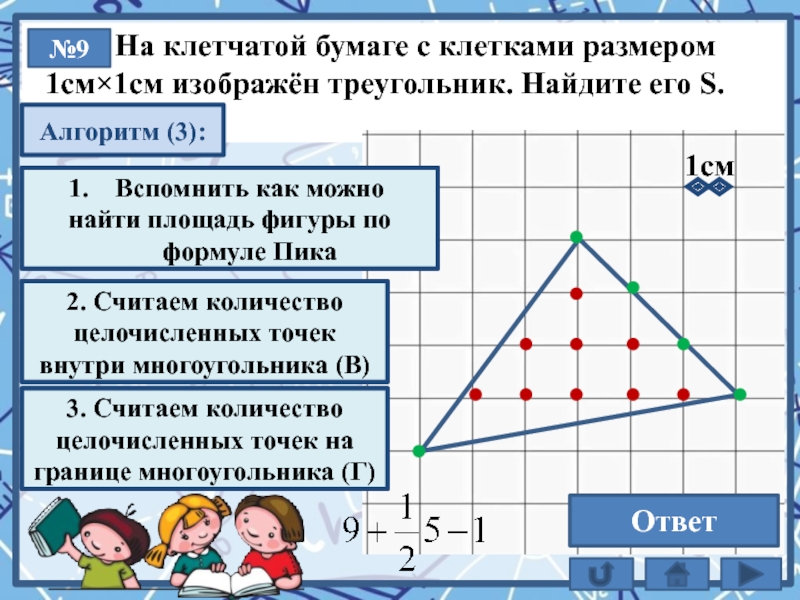
На клетчатой бумаге с клетками размером
1см×1см изображён треугольник. Найдите его S.

№9

10,5

Ответ

Алгоритм (3):

Площадь многоугоугольника с целочисленными вершинами равна сумме В + Г/2 – 1

Вспомнить как можно
найти площадь фигуры по формуле Пика

2. Считаем количество целочисленных точек внутри многоугольника (В)

1cм

3. Считаем количество целочисленных точек на границе многоугольника (Г)

Слайд 12

Текст слайда:

№10

KarMaN01@yandex.ru

Информация

Слайд 13

Текст слайда:

На клетчатой бумаге с клетками размером 1см×1см
изображён параллелограмм. Найдите его высоту,
опущенную на большую сторону.

№11

Ответ

Алгоритм (3):

3. Сравнить стороны и записать ответ к задаче.

1. Высота параллелограмма – перпендикуляр из вершины к противоположной стороне.

Вспомнить что называют высотой параллелограмма.

2. Провести высоты и из тр-ка АВН определить
сторону АВ

1cм

Слайд 14

Текст слайда:

№12

KarMaN01@yandex.ru

Информация

Слайд 15

Текст слайда:

№13

KarMaN01@yandex.ru

Информация

Слайд 16

Текст слайда:

№14

KarMaN01@yandex.ru

Информация

Слайд 17

Текст слайда:

№15

KarMaN01@yandex.ru

Информация

Слайд 18

Текст слайда:

№16

KarMaN01@yandex.ru

Информация

Слайд 19

Текст слайда:

№17

KarMaN01@yandex.ru

Информация

Слайд 20

Текст слайда:

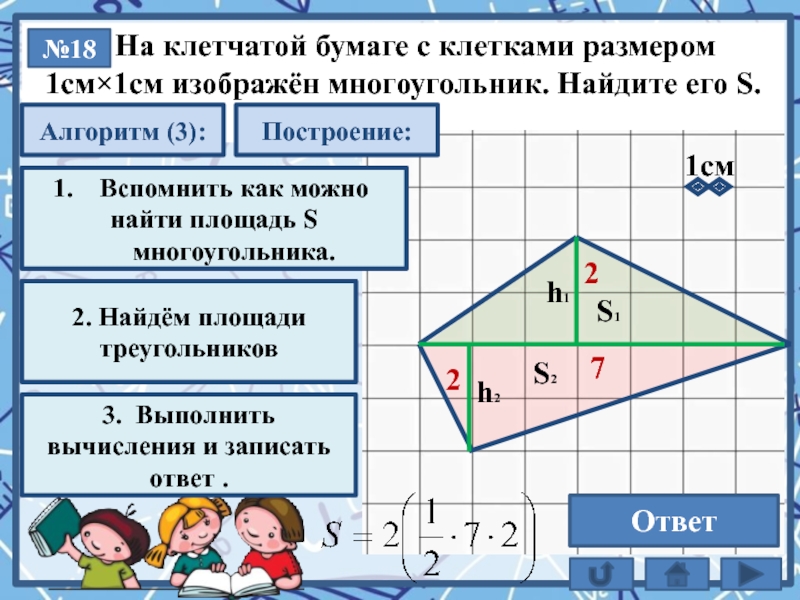
На клетчатой бумаге с клетками размером
1см×1см изображён многоугольник. Найдите его S.

№18

Ответ

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

1. Площадь многоугольника равна сумме площадей фигур из которых состоит (S1 + S2)

Вспомнить как можно
найти площадь S многоугольника.

2. Найдём площади треугольников

Построение:

1cм

Слайд 21

Текст слайда:

№19

KarMaN01@yandex.ru

Информация

Слайд 22

Текст слайда:

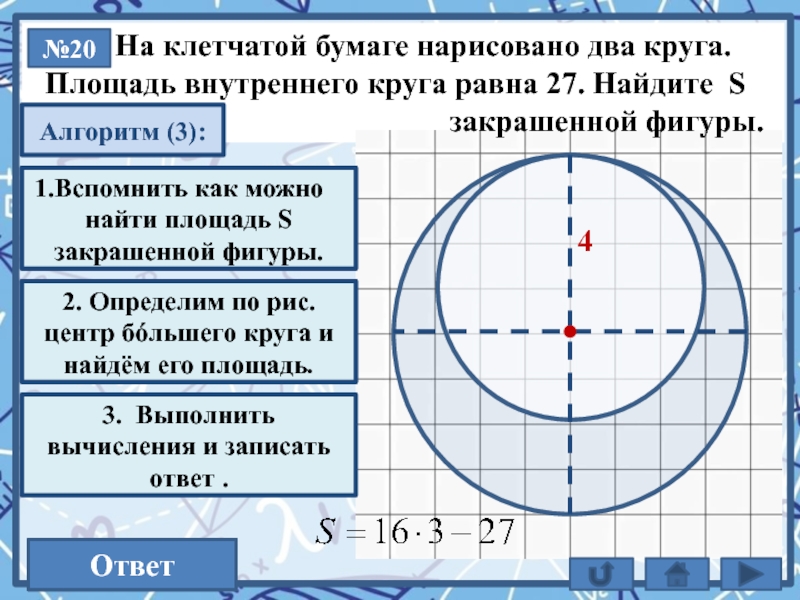
На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 27. Найдите S
закрашенной фигуры.

№20

Алгоритм (3):

3. Выполнить вычисления и записать ответ .

S = Sб – Sм

Вспомнить как можно
найти площадь S закрашенной фигуры.

2. Определим по рис. центр бóльшего круга и найдём его площадь.

Ответ

Слайд 23

Текст слайда:

Уважаемые пользователи, дорогие коллеги!
Если Вам понравился ресурс, то получить полную версию
Вы можете, написав мне на электронную почту:

Пожалуйста, в письме указывайте ФИО
Описание:
Презентация состоит из 24 рабочих слайдов
В ресурсе представлено 20 задач по заявленной теме
с подробным разбором решения.
Задачи соответствуют спецификации и кодификатору к демонстрационному варианту КИМ-2020 по математике, представленного на сайте ФИПИ
Предлагаю подробный разбор заданий №8 и №10
Спасибо за интерес к работе.
Желаю Вам интересных уроков и успешных учеников!
С уважением, КарМаН

KarMaN01@yandex.ru

Слайд 24

Текст слайда:

Титульный слайд

Фон слайдов

источники

Дети в классе

Презентация на тему Задание №18 ОГЭ математика 2021 с решениями, из раздела: Образование. Эта презентация содержит 27 слайда(ов). Информативные слайды и изображения помогут Вам заинтересовать аудиторию. Скачать конспект-презентацию на данную тему можно внизу страницы, поделившись ссылкой с помощью социальных кнопок. Также можно добавить наш сайт презентаций в закладки! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них. Все права принадлежат авторам презентаций.

Слайды и текст этой презентации
Открыть в PDF

Слайд 2

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до прямой ВС.

ЗАДАЧА №1

Слайд 3

Текст слайда:

ЗАДАЧА №1

ОТВЕТ: 3.

Слайд 4

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.

ЗАДАЧА №2

Слайд 5

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите длину его большей диагонали.

ЗАДАЧА №2

ОТВЕТ: 10.

Слайд 6

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки А, В и С. Найдите расстояние от точки А до середины ВС.

ЗАДАЧА №3

Слайд 7

Текст слайда:

ЗАДАЧА №3

ОТВЕТ: 6.

Слайд 8

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.

ЗАДАЧА №4

Слайд 9

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите его площадь.

ЗАДАЧА №4

ОТВЕТ: 21.

Слайд 10

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.

ЗАДАЧА №5

Слайд 11

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите ее площадь.

ЗАДАЧА №5

ОТВЕТ: 33.

Слайд 12

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.

ЗАДАЧА №6

Слайд 13

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена фигура. Найдите ее площадь.

ЗАДАЧА №6

ОТВЕТ: 26.

Слайд 14

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.

ЗАДАЧА №7

Слайд 15

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.

ЗАДАЧА №7

ОТВЕТ: 42.

Слайд 16

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.

ЗАДАЧА №8

Слайд 17

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен ромб. Найдите площадь ромба.

ЗАДАЧА №8

ОТВЕТ: 20.

Слайд 18

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите длину его средней линии, параллельной стороне АС.

ЗАДАЧА №9

Слайд 19

Текст слайда:

ЗАДАЧА №9

ОТВЕТ: 4,5.

Слайд 20

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.

ЗАДАЧА №10

Слайд 21

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображена трапеция. Найдите длину ее средней линии.

ЗАДАЧА №10

ОТВЕТ: 5,5.

Слайд 22

Текст слайда:

Найти тангенс угла АОВ, изображенного на рисунке.

ЗАДАЧА №11

Слайд 23

Текст слайда:

Найти тангенс угла АОВ, изображенного на рисунке.

ЗАДАЧА №11

ОТВЕТ: 3,5.

Слайд 24

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.

ЗАДАЧА №12

Слайд 25

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен параллелограмм. Найдите площадь этого параллелограмма.

ЗАДАЧА №12

ОТВЕТ: 14.

Слайд 26

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.

ЗАДАЧА №13

Слайд 27

Текст слайда:

На клетчатой бумаге с размером клетки 1 x 1 изображен треугольник. Найдите площадь этого треугольника.

ЗАДАЧА №13

ОТВЕТ: 17,5.

Источник

Урок 1	Геометрический смысл производной	—
Задание 1	Справочный материал: геометрический смысл производной
Задание 2	Прямая y = 7x — 5 параллельна касательной к графику функции. Найти абсциссу точки касания — Предварительный просмотр
Задание 3	Прямая ?=−4?−11 является касательной к графику квадратичной функции. Найти абсциссу точки касания
Задание 4	Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Задание 5	На рисунке изображен график производной функции . Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = — 2x – 11 или совпадает с ней.
Задание 6	Как найти значение производной в данной точке, если к графику функции проведена касательная
Задание 7	Найдите значение производной функции в точке ?_0=8.
Задание 8	На рисунке изображен график производной функции f(x)
Урок 2	Признаки возрастания и убывания функции. Точки экстремума.	—
Задание 1	Справочный материал: признаки возрастания и убывания функции, точки экстремума
Задание 2	В какой точке отрезка функция принимает наибольшее значение
Задание 3	В какой точке отрезка функция принимает наименьшее значение
Задание 4	Найдите сумму точек экстремума
Задание 5	Найти количество точек максимума функции по графику производной
Задание 6	Найти сумму целых целых точек на промежутках возрастания функции по графику производной
Задание 7	Найти длину наибольшего промежутка возрастания функции
Задание 8	Определите количество целых точек, в которых производная функции положительна.
Задание 9	Определите количество целых точек, в которых производная функции f(x) отрицательна.
Задание 10	Найти количество точек минимума функции по графику производной
Задание 11	Найти количество точек максимума функции по графику производной
Задание 12	По графику производной найти точку экстремума функции
Задание 13	По графику производной найти количество точек экстремума
Задание 14	В скольких точках производная функции отрицательна?
Задание 15	В скольких точках производная функции положительна?
Задание 16	По графику производной определить, в скольких точках функция возрастает
Задание 17	По графику производной определить, в скольких точках функция убывает
Задание 18	Определить по графику функции, в какой точке значение производной наибольшее
Задание 19	Определить по графику функции, в какой точке значение производной наименьшее
Урок 3	Физический смысл производной	—
Задание 1	Физический смысл производной
Задание 2	По уравнению координаты найти скорость точки
Задание 3	По уравнению координаты найти время движения точки
Задание 4	Сколько раз скорость точки обращалась в ноль
Урок 4	Первообразная	—
Задание 1	По графику y=F(x) найти количество решений уравнения f(x)=0
Задание 2	Пользуясь рисунком, вычислите F(8)-F(2)
Задание 3	По графику функции найти площадь закрашенной фигуры.

Источник

Слайды и текст этой презентации Открыть в PDF

Слайды и текст этой презентации
Открыть в PDF