Первый способ:
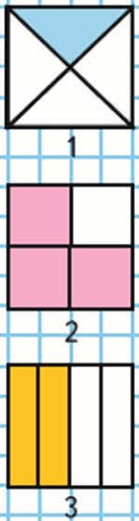
Всё поле разделено на квадраты со стороной 1 см. То есть площадь такого квадрата 1 кв. см.
Чтобы узнать площадь заштрихованной фигуры, достаточно посчитать количество заштрихованных
квадратов. В первой фигуре их всего 21, значит площадь заштрихованной фигуры 21
кв. см. Площадь второй фигуры попробуй сам вычислить точно так же.
Второй способ несколько длинней:
Мы видим квадрат со стороной 5
см.
Еще мы видим два не заштрихованных прямоугольника с сторонами 1 кв. см и 2 кв. см.
5х5=25 (кв. см) – площадь этого квадрата.
1х2=2 (кв. см) – площадь каждого не заштрихованного прямоугольника.
2х2=4 (кв. см) – площадь всей не заштрихованной части квадрата
Теперь чтобы найти площадь заштрихованной фигуры, нужно от площади квадрата
отнять площадь его не заштрихованной части.
25-4=21 (кв. см).
Площадь второй фигуры попробуй сам вычислить точно так же, с той лишь разницей,
что там изначально дан прямоугольник со сторонами 5 см и 7 см.
Узнай площадь каждого квадрата и закрашенной его части.
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 2. Страница 20. Номер №8
Решение
1) 2 * 2 = 4
(
с
м
2
)
− площадь первого квадрата;
2) 4 : 4 = 1
(
с
м
2
)
− площадь закрашенной части.
1) 2 * 2 = 4
(
с
м
2
)
− площадь первого квадрата;
2) 4 : 4 = 1
(
с
м
2
)
− площадь не закрашенной части;
3) 1 * 3 = 3
(
с
м
2
)
− площадь закрашенной части.
1) 2 * 2 = 4
(
с
м
2
)
− площадь первого квадрата;
2) 4 : 4 = 1
(
с
м
2
)
− площадь не закрашенной части;
3) 1 * 2 = 2
(
с
м
2
)
− площадь закрашенной части.
The area of the shaded region is the difference between two geometrical shapes which are combined together. By subtracting the area of the smaller geometrical shape from the area of the larger geometrical shape, we will get the area of the shaded region. Or subtract the area of the unshaded region from the area of the entire region that is also called an area of the shaded region.
Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).
Do Refer:
- Area of a Square
- Areas of Irregular Figures
- Area of a Polygon
Follow the below steps and know the process to find out the Area of the Shaded Region. We have given clear details along with the solved examples below.
- Firstly, find out the area of the large geometrical shape or outer region.
- Then, find the area of the small geometrical shape or inner region of the image.
- Finally, subtract an area of the small geometrical shape (entire region) from the large area of the small geometrical shape (shaded region).
- The resultant value is considered as the area of the shaded region.
Area of the Shaded Region Examples
Problem 1.
A regular hexagon is inscribed in a circle with a radius of 21cm. Find out the area of the shaded region?
Solution:
As per the given information,
Hexagon is inscribed in a circle.
Radius of the circle = 21cm.
Area of the circle = A=πr².
Substituting the radius (r) value in the above equation, we will get
A = π(21)².
A = 22 / 7(21 * 21).
A = 22(3*21).
A = 1386.
Area of the circle (A) = 1386 cm².
Area of the hexagon = 3√3/ 2 r².
Substitute the radius value in the above equation, we will get
A = 3√3/ 2 (21)².
A = 3√3/ 2 (441).
A = 1145.75
The area of the hexagon is equal to 1145 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 1386 – 1145 = 241 cm².
Therefore, the area of the shaded region is equal to 241 cm².
Problem 2.
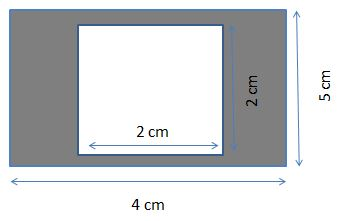
The square is inscribed in a rectangle. The side of the square is 2cm. The length and breadth of the rectangle is 4cm and 5cm. Find out the area of the shaded region?
Solution:
As per the given details,
The Square is inscribed in a rectangle.
Side of the square a = 2cm.
Length of the rectangle (l) = 4cm and breadth of the rectangle (b) =5cm.
Area of the square (A) = a²
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (2)² = 4cm².
Area of the rectangle (A) = l * b
Substitute the length and breadth values in the above equation, we will get
Area of the rectangle (A) = 4cm * 5cm = 20 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 20 – 4 = 16 cm².
Therefore, the Area of the shaded region is equal to 16cm².
Problem 3.
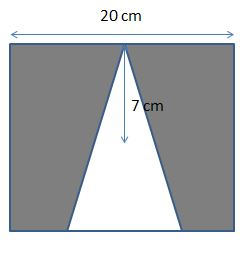
A Triangle is inscribed in a Square. The side of the square is 20cm and the radius of the triangle is 7cm. Calculate the area of the shaded region?
Solution:
As per the given information,
A triangle is inscribed in a square.
Side of the square (a) = 20cm.
Radius of the triangle (r) = 7cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (20)² = 400cm².
Area of the triangle (A)=πr².
Substitute the radius value in the above equation. Then we will get,
A = 22 / 7 (7)².
A = 22 * 7 =154.
The area of the triangle is equal to 154 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 400 – 154 = 246 cm².
Therefore, the Area of the shaded region is equal to 246 cm².
Problem 4.
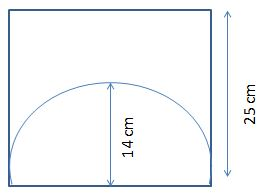
A semi-circle is inscribed in a square with a radius of 14cm. The side of the square is 25cm. Calculate the area of the shaded region?
Solution:
As per the given details,
A semi-circle is inscribed in a square.
Radius of the semi-circle (r) = 14cm.
Side of the square (a) = 25cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (25)² = 625 cm².
Area of the Semi – circle (A) = πr² / 2.
Substitute the radius of the semi-circle in the above equation, we will get
A = 22 / 7 (14)² / 2.
A = 22 / 7 (14 * 14) / 2.
A = 22 (2 * 14) / 2.
A = 22 * 14 = 308.
The area of the semi-circle is equal to 308 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 625 – 308 = 317 cm².
So, the Area of the shaded region is equal to 317 cm².
FAQs on finding the Area of a Shaded Region
1. What is the Area of the Shaded Region?
It is the difference between the area of the outer region and the inner region.
2. How to find the Area of the Shaded Region?
There are three steps to find the area of the shaded region. They are
i. Calculate the area of the outer region.
ii. Calculate the area of the inner region.
iii. Subtract the area of the inner region from the outer region.
3. What is the Formula for the Area of the Shaded Region?
The formula for the area of the shaded region is
Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).
Распространенной проблемой геометрии начала является вычисление площади стандартных фигур, таких как квадраты и круги. Промежуточным шагом в этом процессе обучения является объединение двух форм. Например, если вы нарисуете квадрат, а затем нарисуете круг внутри квадрата, чтобы круг касался всех четырех сторон квадрата, вы можете определить общую площадь за пределами круга внутри квадрата.
-
Распространенной ошибкой в этой задаче является использование диаметра круга в уравнении площади, а не радиуса. Будьте осторожны, чтобы убедиться, что у вас есть вся правильная информация, прежде чем начать работу.
Сначала вычислите площадь квадрата, умножив его длину стороны s:
площадь = с 2
Например, предположим, что сторона вашего квадрата равна 10 см. Умножьте 10 см х 10 см, чтобы получить 100 квадратных сантиметров.
Рассчитайте радиус круга, который равен половине диаметра:
радиус = 1/2 диаметра
Поскольку круг полностью помещается внутри квадрата, его диаметр составляет 10 см. Радиус составляет половину диаметра, который составляет 5 см.
Рассчитаем площадь круга, используя уравнение:
площадь = πr 2
Значение pi (π) составляет 3, 14, поэтому уравнение становится 3, 14 x 5 см 2. Итак, у вас квадрат 3, 14 х 25 см, что равно 78, 5 квадратных сантиметров.
Вычтите площадь круга (78, 5 см в квадрате) из площади квадрата (100 см в квадрате), чтобы определить площадь за пределами круга, но все еще внутри квадрата. Это становится 100 см 2 — 78, 5 см 2, что равно 21, 5 см в квадрате.
Предупреждения
Найдите площадь заштрихованной части квадрата!
Вопрос Найдите площадь заштрихованной части квадрата?, расположенный на этой странице сайта, относится к
категории Математика и соответствует программе для 5 — 9 классов. Если
ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска
похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему.
Для этого ключевые фразы введите в строку поиска, нажав на кнопку,
расположенную вверху страницы. Воспользуйтесь также подсказками посетителей,
оставившими комментарии под вопросом.