Содержание
- Расчет площади поперечного сечения круга
- Определение величины
- Область применения
- Способы расчета
- Как рассчитать поперечное сечение проводника
- Площадь поперечного сечения как электротехническая величина
- Цели расчета
- Соотношение диаметра кабеля с площадью его сечения
- Расчет сечения многожильного проводника
- Особенности самостоятельного расчета
- При помощи штангенциркуля
- С использованием линейки и карандаша
- Таблица соответствия диаметра проводов и площади их сечения
- Определение сечения проводника на вводе
- Вычисление сечения провода для линии розеток
- Подбор сечения для трехфазной линии 380 В с несколькими приборами
- Сечение проводов в домах старой застройки и предельная нагрузка
- Какой кабель выбрать для квартирной проводки
Расчет площади поперечного сечения круга
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
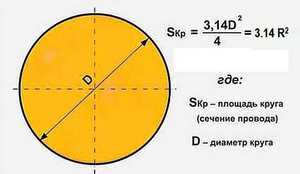
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
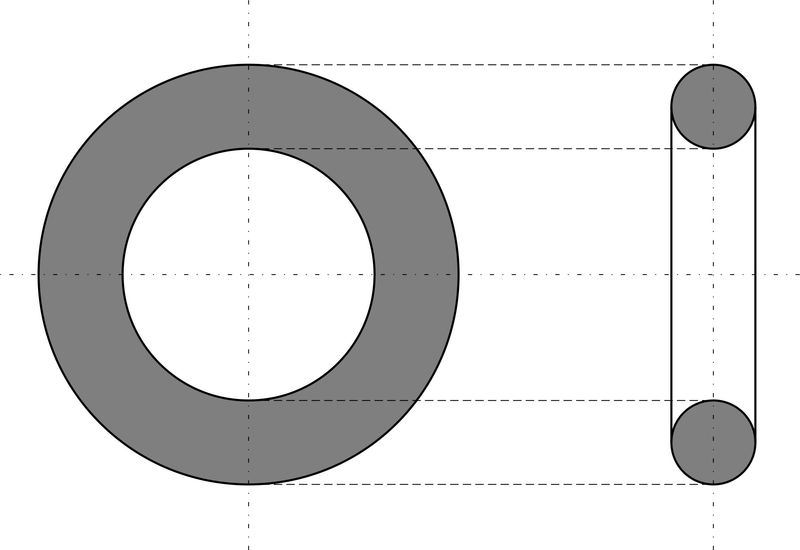
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Источник
Как рассчитать поперечное сечение проводника
Для правильного выбора и организации электролинии необходимо учитывать параметры и нагрузку проводников. Они представляют собой металлическую нить из меди, алюминия, стали, цинка, титана, никеля и обеспечивают передачу тока от его источника до потребителя. У проводников есть поперечное сечение – это фигура, образованная от их рассечения плоскостью поперечного направления. Если его подобрать неправильно, линия выйдет из строя или загорится при скачках напряжения.
Площадь поперечного сечения как электротехническая величина
В качестве примера сечения можно рассмотреть распил изделия под углом 90 градусов относительно поперечной оси. Контур фигуры, получившейся в результате, определяется конфигурацией объекта. Кабель имеет вид небольшой трубы, поэтому при распиле выйдет фигура в виде двух окружностей определенной толщины. При поперечном рассечении круглого металлического прута получится форма круга.
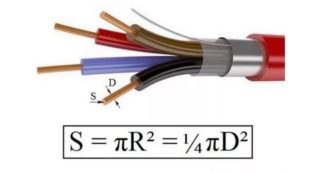
В электротехнике площадь ПС будет значить прямоугольное сечение проводника в отношении к его продольной части. Сечение жил всегда будет круглым. Измерение параметра осуществляется в мм2.
Начинающие электрики могут перепутать диаметр и сечение элементов. Чтобы определить, какая площадь сечения у жилы, понадобиться учесть его круглую форму и воспользоваться формулой:
- S – площадь круга;
- π — постоянная величина 3,14;
- R – радиус круга.
Если известен показатель площади, легко найти удельное сопротивление материала изготовления и длину провода. Далее вычисляется сопротивление тока.
Для удобства расчетов начальная формула преобразуется:
- Радиус – это ½ диаметра.
- Для вычисления площади π умножается на D (диаметр), разделенный на 4, или 0,8 умножается на 2 диаметра.
При вычислениях используют показатель диаметра, поскольку его неправильный подбор может вызвать перегрев и воспламенение кабеля.
Цели расчета
Рассчитывать параметры площади сечения проводника необходимо с несколькими целями:
- получение необходимого количества электричества для запитки бытовых приборов;
- исключение переплат за неиспользуемый энергоноситель;
- безопасность проводки и предотвращение возгораний;
- возможность подключения высокомощной техники к сети;
- предотвращение оплавления изоляционного слоя и коротких замыканий;
- правильная организация осветительной системы.
Оптимальное сечение провода для освещения – 1,5 мм2 для линии, 4-6 мм2 на вводе.
Соотношение диаметра кабеля с площадью его сечения
Определение посредством формулы площади поперечного сечения проводников занимает длительное время. В некоторых случаях уместно использовать данные из таблицы. Поскольку для организации современной проводки применяется медный кабель, в таблицу вносятся параметры:
- диаметр;
- сечение в соответствии с показателем диаметра;
- предельная мощность нагрузки проводников в сетях с напряжением 220 и 380 В.
| Диаметр жилы, мм | Параметры сечения, мм2 | Сила тока, А | Мощность медного проводника, кВт | |
| Сеть 220 В | Сеть 380 В | |||
| 1,12 | 1 | 14 | 3 | 5,3 |
| 1,38 | 1,5 | 15 | 3,3 | 5,7 |
| 1,59 | 2 | 19 | 4,1 | 7,2 |
| 1,78 | 2,5 | 21 | 4,6 | 7,9 |
| 2,26 | 4 | 27 | 5,9 | 10 |
| 2,76 | 6 | 34 | 7,7 | 12 |
| 3,57 | 10 | 50 | 11 | 19 |
Посмотрев данные в соответствующих колонках, можно узнать нужные параметры для электролинии жилого здания или производственного объекта.
Расчет сечения многожильного проводника
- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Особенности самостоятельного расчета

При помощи штангенциркуля
Способ оправдан, если будут измеряться параметры усеченного, или бракованного кабеля. К примеру, ВВГ может обозначаться как 3х2,5, но фактически быть 3х21. Вычисления производятся так:
- С проводника снимается изоляционное покрытие.
- Диаметр замеряется штангенциркулем. Понадобится расположить провод между ножками инструмента и посмотреть на обозначения шкалы. Целая величина находится сверху, десятичная – снизу.
- На основании формулы поиска площади круга S = π (D/2)2 или ее упрощенного варианта S = 0,8 D² определяется поперечное сечение.
- Диаметр равен 1,78 мм. Подставляя величину в выражение и округлив результат до сотых, получается 2,79 мм2.
Для бытовых целей понадобятся проводники с сечением 0,75; 1,5; 2,5 и 4 мм2.
С использованием линейки и карандаша
При отсутствии специального измерителя можно воспользоваться карандашом и линейкой. Операции выполняются с тестовым образом:
- Зачищается от изоляционного слоя участок, равный 5-10 см.
- Получившаяся проволока наматывается на карандаш. Полные витки укладываются плотно, пространства между ними быть не должно, «хвостики» направляются вверх или вниз.
- В конечном итоге должно получиться определенное число витков, их требуется посчитать.
- Намотка прикладывается к линейке так, чтобы нулевое деление совпадало с первой намоткой.
- Замеряется длина отрезка и делится на количество витков. Получившаяся величина – диаметр.
- Например, получилось 11 витков, которые занимают 7,5 мм. При делении 7,5 на 11 выходит 0,68 мм – диаметр кабеля. Сечение можно найти по формуле.
Точность вычислений определяется плотностью и длиной намотки.
Таблица соответствия диаметра проводов и площади их сечения
Если нет возможности пройти тестирование диаметра или сделать вычисление при покупке, допускается использовать таблицу. Данные можно сфотографировать, распечатать или переписать, а затем применять, чтобы найти нормативный или популярный размер жилы.
| Диаметр кабеля, мм | Сечение проводника, мм2 |
| 0,8 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1 |
| 1,38 | 1,5 |
| 1,6 | 2 |
| 1,78 | 2,5 |
| 2,26 | 4 |
| 2,76 | 6 |
| 3,57 | 10 |
При покупке электрокабеля понадобится посмотреть параметры на этикетке. К примеру, используется ВВНГ 2х4. Количество жил – величина после «х». То есть, изделие состоит из двух элементов с поперечным сечением 4 мм2. На основании таблицы можно проверить точность информации.
Чаще всего диаметр кабеля меньше, чем заявлен на упаковке. У пользователя два варианта – применять другой или выбрать с большей площадью сечения кабель по диаметру. Выбрав второй, понадобится проверить изоляцию. Если она не сплошная, тонкая, разная по толщине, остановитесь на продукции другого изготовителя.
Определение сечения проводника на вводе
Подбор сечения осуществляется так, чтобы допустимый ток жил за длительный период был больше номинала автомата. Например, в доме на ввод пущен медный трехжильный проводник ВВГнг, уложенный открытым способом. Оптимальное сечение – 4 мм2, поэтому понадобится материал ВВГнг 3х4.
После этого высчитывается показатель условного тока отключения для автомата с номиналом 25 А: 1,45х25=36,25 А. У кабеля с площадью сечения 4 мм2 параметры длительно допустимого тока 35 А, условного – 36,25 А. В данном случае лучше взять вводный проводник из меди сечением 6 мм2 и допустимым предельным током 42 А.
Вычисление сечения провода для линии розеток
Каждый электроприбор имеет показатели собственной мощности. Они замеряются в Ваттах и указываются в паспорте либо на наклейке на корпусе. Примером поиска сечения будет линия запитки для стиральной машины мощностью 2,4 кВт. При расчетах учитывается:
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.
Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Подбор сечения для трехфазной линии 380 В с несколькими приборами
Подключение нескольких видов бытовой техники к трехфазной линии предусматривает протекание потребляемого тока по трем жилам. В каждом из них будет меньшая величина, чем в двухжильном. На основании данного явления в трехфазной сети допускается применять кабель с меньшим сечением.
К примеру, в доме устанавливается генератор с мощностью 20 кВт и суммарной мощностью по трем фазам 52 А. На основании значений таблицы выйдет, что оптимальное сечение кабеля – 8,4 мм2. На основании формулы высчитывается фактическое сечение: 8,4/1,75=4,8 мм2. Чтобы подсоединить генератор мощностью 20 кВт на трехфазную сеть 380 В необходим медный проводник, сечение каждой жилы которого 4,8 мм2.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Какой кабель выбрать для квартирной проводки

В квартирах и домах допускается использовать провод с маркировкой:
- ПУНП – плоский проводник с медными жилами в ПВХ-оболочке. Рассчитан на напряжение номиналом 250 В при частоте 50 Гц.
Источник
В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
- 1. Через радиус
- 2. Через диаметр
- Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Ответ:
Объяснение:
Мы знаем что
Где — радиус
Т.к. , тогда
Мы знем что , отсюда
, теперь согласно уравнению
Как найти площадь круга, зная диаметр?
На этой странице находится вопрос Как найти площадь круга, зная диаметр?, относящийся к категории
Физика. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Физика. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Как рассчитать площадь круга — все формулы
На чтение 3 мин. Просмотров 17.3k.
Площадь круга часто требуется рассчитать в различных задачах и это не только задачи по геометрии, иногда знать как рассчитывается площадь круга важно знать и в некоторых текстовых задачах алгебры. Итак, давайте разбираться.
Что такое площадь круга
Площадь круга — это мера заполненности области внутри окружности, являющейся границей круга, выраженная в квадратных единицах (м2, см2, кв.ед.). В математике эти единицы могут разными, в физике же если вы определяете площадь круга — вы должны указать единицы в системе СИ, а это м2.
Визуально, площадь круга это величина закрашенной области на рисунке:
Как можно найти площадь круга
Если дан радиус круга
Здесь все зависит от того, какие вам величины даны в самом начале. Если вам дан радиус круга, то площадь круга определяется по формуле:
— число
. Число пи является одним из наиболее важных констант в математике, определяется как постоянное отношение длины окружности к ее диаметру в евклидовой плоскости. Другими словами:
π = длина окружности круга/диаметр этого круга.
Таким образом, приблизительное значение , наиболее известное, как: 3,14.
Это приблизительное значение, потому что число π — это то, что мы называем иррациональным числом. Оно не может быть записано как отношение двух целых чисел. Сегодня мы знаем более 12 000 миллиардов знаков после запятой. Однако до сих пор нет определенной модели, которая давала бы все эти значения.
Найти площадь круга можно и с помощью нашего онлайн калькулятора.
Найти площадь круга, зная его радиус. Онлайн калькулятор.
Введите радиус:
Площадь круга:
Площадь круга в π:
Если дан диаметр круга
Если известен диаметр круга, то площадь круга можно найти по формуле:
Найти площадь круга через диаметр онлайн
Площадь круга:
Площадь круга в π:
Если дана длина окружности
Так как длина окружности определяется по формуле: , то можно выразить радиус круга:
. Тогда площадь:
.
Найти площадь круга через длину окружности — онлайн калькулятор
Длина окружности круга (введите число):
Площадь круга:
Площадь круга в π:
Примеры расчета
Пример 1.
Рассчитать площадь круга, если известен радиус круга .
Решение: По формуле (1) находим .
Пример 2.
Найдите площадь, если дан диаметр круга .
Решение: По формуле (2) находим .
Вы видите, что находить площадь круга совсем не сложно, если известны все формулы и даны все необходимые для расчета величины.
( 12 оценок, среднее 4.58 из 5 )

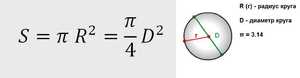




![Rendered by QuickLaTeX.com [boxed {S = pi frac{d^2}{4}} eqno (2)]](https://mathematics-repetition.com/wp-content/ql-cache/quicklatex.com-ea25733713ee06613a3902df2df79d2b_l3.png)