Как найти площадб равнобедренного треугольника

Как посчитать площадь равнобедренного треугольника

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как посчитать площадь равнобедренного треугольника

Чтобы посчитать площадь равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

равнобедренный треугольник

Чтобы вычислить площадь равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

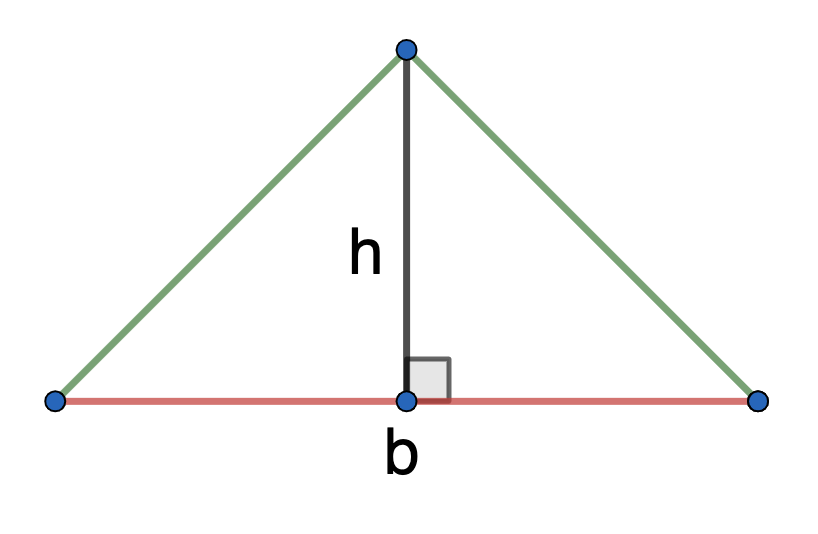
  • длина основания (b) и высота (h)
  • длину двух равных сторон (a) и угол β
  • длину двух равных сторон (a) и угол α
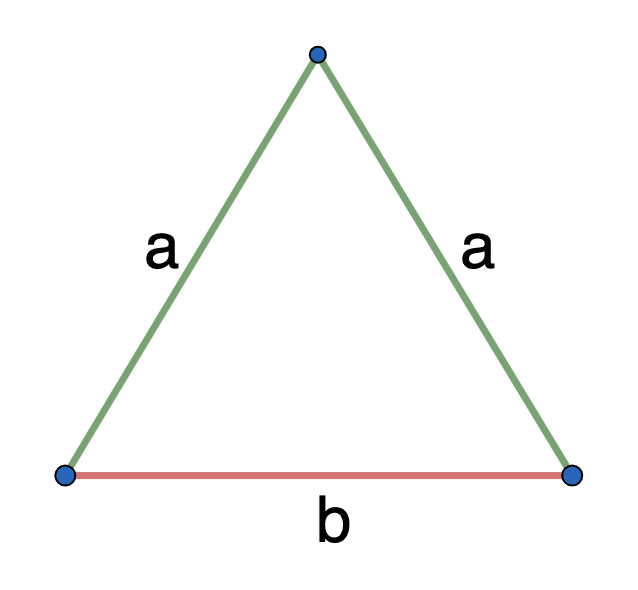
  • длину двух равных сторон (a) и длину основания (b)

Введите их в соответствующие поля и узнаете площадь равнобедренного треугольника (S).

Как посчитать площадь равнобедренного треугольника зная длину основания и высоту

Чему равна площадь равнобедренного треугольника если длина основания

b =

, а длина высоты

h =?

Ответ:

S =

0

Какова площадь равнобедренного треугольника (S) если известны длина основания (b) и высота (h)?

Формула

S = ½⋅b⋅h

Пример

Если основание b = 5 см, а высота h = 10 см, то:

S = ½⋅5⋅10 = 50/2 = 25 см2

Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между ними (β)

Чему равна площадь равнобедренного треугольника если длина сторон

a =

, а угол между ними

β =° ?

Ответ:

S =

0

Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между ними (β)?

Формула

S = ½⋅a2⋅sin β

Пример

Если сторона а = 10 см, а ∠β = 30°, то:

S = ½⋅102⋅sin30° = ½ ⋅100⋅0.5= 50/2 = 25 см2

Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между стороной и основанием (α)

Чему равна площадь равнобедренного треугольника если длина сторон

a =

, а угол

α =° ?

Ответ:

S =

0

Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между стороной и основанием (α)?

Формула

S = ½⋅a2⋅sin(180-2α)

Пример

Если сторона а = 10 см, а ∠α = 75°, то:

S = ½⋅102⋅sin(180-2⋅75)° = ½ ⋅100⋅0.5 = 50/2 = 25 см2

Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и длину основания (b)

Чему равна площадь равнобедренного треугольника если длина сторон

a =

, а длина основания

b =?

Ответ:

S =

0

Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и длина основания (b)?

Формула

S = ½⋅b⋅√(a+½⋅b)⋅(a-½⋅b)

Пример

Если сторона а = 10 см, а основание b = 5, то:

S =½⋅5⋅√(10+½⋅5)⋅(10-½⋅5)= 2.5⋅√12.5⋅7.5 ≈ 24.2 см2

См. также

Источник

Формула площади равнобедренного треугольника

  • по основанию и высоте

(S_bigtriangleup = frac{1}{2} b*h)

(b) — основание
(h) — высота

  • по двум сторонам

(S_bigtriangleup = frac{b}{4} sqrt{ 4a^2-b^2})

(b) — основание
(a) — стороны
(h) — высота

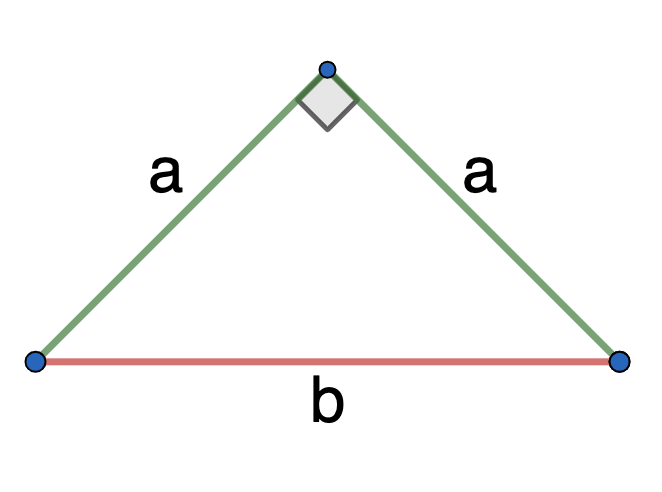
  • если в равнобедренном треугольнике прямой угол

(S_bigtriangleup = frac{1}{2} a^2)

(a) — равные стороны, между которыми 90°

Примеры

Найдите площадь равнобедренного треугольника, если боковая сторона равна 10, а основание 12.

Решение: Воспользуемся формулой подсчета по двум сторонам (S_bigtriangleup = frac{b}{4} sqrt{ 4a^2-b^2} = frac{10}{4} sqrt{ 4*12^2-10^2} = 54,5 )

Как найти площадь равнобедренного треугольника, зная, что основание равно 30, а высота, проведенная к основанию — 12.

Используем формулу (S_bigtriangleup = frac{1}{2} b*h = frac{1}{2} 30*12 = 180) . Ответ 180.

Чему равно основание равнобедренного треугольника, если нам известно, что его площадь равна 180, а высота, проведенная к основанию равна 30.

Решение: Используем первую формулу, из нее следует что (b = frac{S*2}{h} = 180*2/30 = 12)

b — основание
S — площадь треугольника
h — высота

Источник

Как найти площадь любого треугольника

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

  1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
  2. Поделите результат на два.
  • S — искомая площадь треугольника.
  • a — сторона треугольника.
  • h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

  1. Посчитайте произведение двух известных сторон треугольника.
  2. Найдите синус угла между выбранными сторонами.
  3. Перемножьте полученные числа.
  4. Поделите результат на два.
  • S — искомая площадь треугольника.
  • a и b — стороны треугольника.
  • α — угол между сторонами a и b.

Зная три стороны (формула Герона)

  1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
  2. Найдите произведение полученных чисел.
  3. Умножьте результат на полупериметр.
  4. Найдите корень из полученного числа.
  • S — искомая площадь треугольника.
  • a, b, c — стороны треугольника.
  • p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

  1. Найдите произведение всех сторон треугольника.
  2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
  • S — искомая площадь треугольника.
  • R — радиус описанной окружности.
  • a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

  • S — искомая площадь треугольника.
  • r — радиус вписанной окружности.
  • p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

  1. Посчитайте произведение катетов треугольника.
  2. Поделите результат на два.
  • S — искомая площадь треугольника.
  • a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

  1. Умножьте основание на высоту треугольника.
  2. Поделите результат на два.
  • S — искомая площадь треугольника.
  • a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
  • h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

  1. Умножьте квадрат стороны треугольника на корень из трёх.
  2. Поделите результат на четыре.
  • S — искомая площадь треугольника.
  • a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

  • 7 причин полюбить математику
  • ТЕСТ: Помните ли вы геометрию?
  • 10 хитрых головоломок со спичками для тренировки воображения
  • Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
  • ТЕСТ: Сможете ли вы решить простые математические примеры?

Источник


Загрузить PDF


Загрузить PDF

Равнобедренный треугольник – это треугольник, у которого две стороны равны. Равные (боковые) стороны пересекают третью сторону (основание) под одним углом, а точка пересечения равных сторон находится над серединой основания. В этом можно убедиться с помощью линейки и двух карандашей одинаковой длины: если наклонить треугольник в одну или другую сторону, кончики карандашей не соединятся. Такие свойства равнобедренного треугольника позволяют вычислить его площадь всего лишь по нескольким известным величинам.

  1. Изображение с названием Find the Area of an Isosceles Triangle Step 1

    1

    Выясните, как найти площадь параллелограмма. Квадраты и прямоугольники являются параллелограммами, как и любая другая четырехсторонняя фигура, у которой противоположные стороны параллельны. Площадь параллелограмма вычисляется по формуле: S = bh,[1]
     где «b» – основание (нижняя сторона параллелограмма), «h» – высота (расстояние от верхней до нижней стороны; высота всегда пересекает основание под углом 90°).

    • В квадратах и прямоугольниках высота равна боковой стороне, так как боковые стороны пересекают верхнюю и нижнюю стороны под прямым углом.

  2. Изображение с названием Find the Area of an Isosceles Triangle Step 2

    2

    Сравните треугольники и параллелограммы. Между этими фигурами существует простая связь. Если любой параллелограмм разрезать по диагонали, получатся два равных треугольника. Аналогично, если сложить два равных треугольника, получится параллелограмм. Поэтому площадь любого треугольника вычисляется по формуле: S = ½bh, что составляет половину площади параллелограмма.

  3. Изображение с названием Find the Area of an Isosceles Triangle Step 3

    3

    Найдите основание равнобедренного треугольника. Теперь вы знаете формулу для вычисления площади треугольника; осталось выяснить, что такое «основание» и «высота». Основание (обозначается как «b») – это сторона, которая не равна двум другим (равным) сторонам.

    • Например, если стороны равнобедренного треугольника равны 5 см, 5 см, 6 см, в качестве основания выберите сторону, которая равна 6 см.
    • Если все стороны треугольника равны (равносторонний треугольник), в качестве основания выберите любую сторону. Равносторонний треугольник является частным случаем равнобедренного треугольника, но его площадь вычисляется так же.[2]

  4. Изображение с названием Find the Area of an Isosceles Triangle Step 4

    4

    Опустите перпендикуляр на основание. Сделайте это из вершины треугольника, которая противоположна основанию. Помните, что перпендикуляр пересекает основание под прямым углом. Такой перпендикуляр является высотой треугольника (обозначается как «h»). Как только вы найдете значение «h», вы сможете вычислить площадь треугольника.

    • В равнобедренном треугольнике высота пересекает основание точно посередине.

  5. Изображение с названием Find the Area of an Isosceles Triangle Step 5

    5

    Посмотрите на половину равнобедренного треугольника. Обратите внимание, что высота разделила равнобедренный треугольник на два равных прямоугольных треугольника. Посмотрите на один из них и найдите его стороны:

    • Короткая сторона равна половине основания: {frac {b}{2}}.
    • Вторая сторона – это высота «h».
    • Гипотенуза прямоугольного треугольника является боковой стороной равнобедренного треугольника; обозначим ее как «s».

  6. Изображение с названием Find the Area of an Isosceles Triangle Step 6

    6

    Воспользуйтесь теоремой Пифагора. Если известны две стороны прямоугольного треугольника, его третью сторону можно вычислить по теореме Пифагора: (сторона 1)2 + (сторона 2)2 = (гипотенуза)2. В нашем примере теорема Пифагора запишется так: ({frac {b}{2}})^{2}+h^{2}=s^{2} .

    • Скорее всего, теорема Пифагора вам известна в такой записи: a^{2}+b^{2}=c^{2}. Мы употребляем слова «сторона 1», «сторона 2» и «гипотенуза», чтобы предотвратить путаницу с переменными из примера.

  7. Изображение с названием Find the Area of an Isosceles Triangle Step 7

    7

    Вычислите значение «h». Помните, что в формуле для вычисления площади треугольника есть переменные «b» и «h», но значение «h» неизвестно. Перепишите формулу, чтобы вычислить «h»:

  8. Изображение с названием Find the Area of an Isosceles Triangle Step 8

    8

    В формулу подставьте известные значения и вычислите «h». Эту формулу можно применить к любому равнобедренному треугольнику, стороны которого известны. Вместо «b» подставьте значение основания, а вместо «s» – значение боковой стороны, чтобы найти значение «h».

  9. Изображение с названием Find the Area of an Isosceles Triangle Step 9

    9

    Подставьте значения основания и высоты в формулу для вычисления площади треугольника. Формула: S = ½bh; подставьте в нее значения «b» и «h» и вычислите площадь. В ответе не забудьте написать квадратные единицы измерения.

    • В нашем примере основание равно 6 см, а высота равна 4 см.
    • S = ½bh
      S = ½(6 см)(4 см)
      S = 12 см2.

  10. Изображение с названием Find the Area of an Isosceles Triangle Step 10

    10

    Рассмотрим более сложный пример. В большинстве случаев вам будет дана более трудная задача, чем рассмотренная в нашем примере. Чтобы вычислить высоту, нужно извлечь квадратный корень, который, как правило, не извлекается нацело. В этом случае запишите значение высоты в виде упрощенного квадратного корня. Вот новый пример:

    Реклама

  1. Изображение с названием Find the Area of an Isosceles Triangle Step 11

    1

    Вычислите площадь по боковой стороне и прилежащему углу. Если вы знакомы с тригонометрическими функциями, площадь равнобедренного треугольника можно вычислить по боковой стороне и прилежащему углу. Например:[3]

    • Боковая сторона равнобедренного треугольника равна 10 см.
    • Угол θ между двумя равными сторонами равен 120°.

  2. Изображение с названием Find the Area of an Isosceles Triangle Step 12

    2

    Разделите равнобедренный треугольник на два равных прямоугольных треугольника. Для этого опустите перпендикуляр (высоту) из вершины треугольника, которая образована двумя равными сторонами, на основание.

    • Высота делит угол θ ровно пополам. Таким образом, один из углов прямоугольного треугольника равен ½θ, а в нашем примере (½)(120) = 60°.

  3. Изображение с названием Find the Area of an Isosceles Triangle Step 13

    3

    Вычислите высоту «h» с помощью тригонометрических функций. К прямоугольному треугольнику можно применить следующие тригонометрические функции: sin (синус), cos (косинус) и tg (тангенс). В нашем примере известна гипотенуза «s»; нужно найти «h», то есть катет, прилежащий к известному углу. Вспомните, что косинус = прилежащий катет/гипотенуза.

    • cos(θ/2) = h/s
    • cos(60°) = h/10
    • h = 10cos(60º)

  4. Изображение с названием Find the Area of an Isosceles Triangle Step 14

    4

    Вычислите значение второго катета. Теперь мы не знаем значение второго катета прямоугольного треугольника; обозначим его как «x». Вспомните, что синус = противолежащий катет/гипотенуза.

    • sin(θ/2) = x/s
    • sin(60º) = x/10
    • x = 10sin(60°)

  5. Изображение с названием Find the Area of an Isosceles Triangle Step 15

    5

    Обратите внимание, что второй катет прямоугольного треугольника равен половине основания равнобедренного треугольника. То есть b = 2x, потому что высота (первый катет) разделила основание пополам (на два катета, каждый из которых равен значению «x»).

  6. Изображение с названием Find the Area of an Isosceles Triangle Step 16

    6

    Подставьте значения «h» и «b» в формулу для вычисления площади. Теперь, когда вы знаете основание и высоту, подставьте их в формулу S = ½bh:

  7. Изображение с названием Find the Area of an Isosceles Triangle Step 17

    7

    Запишите универсальную формулу. Теперь, когда вы познакомились с полным процессом вычисления площади равнобедренного треугольника, можно пользоваться универсальной формулой, которая позволит сократить этот процесс. Если вы повторите описанный процесс без числовых значений и упростите ряд выражений, вы получите следующую универсальную формулу:[4]

    • S={frac {1}{2}}s^{2}sintheta
    • s – одна из двух боковых (равных) сторон.
    • θ – угол между двумя боковыми (равными) сторонами.

    Реклама

Советы

  • Если дан равнобедренный прямоугольный треугольник (с двумя равными катетами и прямым углом), вычислить его площадь очень просто. Один катет будет основанием, а второй – высотой, поэтому формула S = ½bh запишется так: S=½s2, где s – катет.
  • Из квадратного корня можно извлечь два значения – положительное и отрицательное, но в геометрических задачах отрицательным значением можно пренебречь. Например, высота треугольника не может быть отрицательной.
  • В некоторых задачах будут даны другие величины, например, основание и один угол равнобедренного треугольника. В этом случае действуйте так же: разделите равнобедренный треугольник на два равных прямоугольных треугольника, а затем найдите высоту с помощью тригонометрических функций.

Реклама

Об этой статье

Эту страницу просматривали 25 570 раз.

Была ли эта статья полезной?

Источник

Какие размеры треугольника известны:

Основание и высота

Основание и сторона

Укажите размеры:

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Треугольники бывают прямоугольный, равнобедренный, равносторонний.

Равнобедренный треугольник — это треугольник у которого две стороны равны. Эти равные стороны называют боковыми, а третью сторону равнобедренного треугольника называют основанием.

Формула площади равнобедренного треугольника

Чтобы посчитать площадь равнобедренного треугольника, необходимо знать размеры двух сторон треугольника.

Площадь равнобедренного треугольника расчитывается по формуле:

a
a
b
h

Через основание и высоту:

S = dfrac{1}{2}bh

Через основание и боковую сторону:

S = dfrac{b}{4} sqrt{4a^2 — b^2}

  • S — площадь треугольника
  • a — равные стороны
  • b — основание треугольника
  • h — высота

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти неизвестное число без уравнения
  • Как найти адиабатный показатель
  • Как найти второй аирподс в комнате
  • Как найти вписанную в треугольник окружность делит
  • Как найти хлорид кальция формула