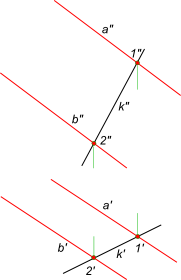
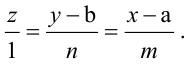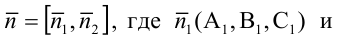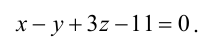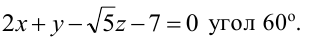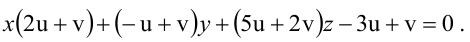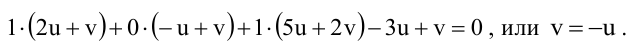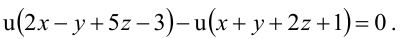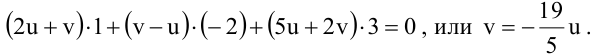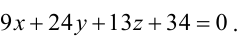3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
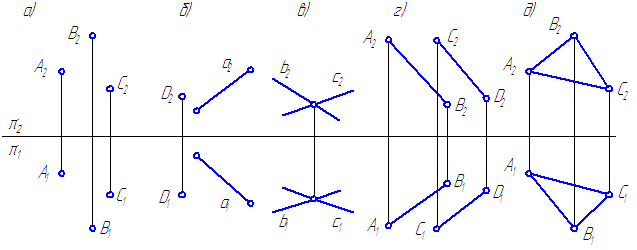
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
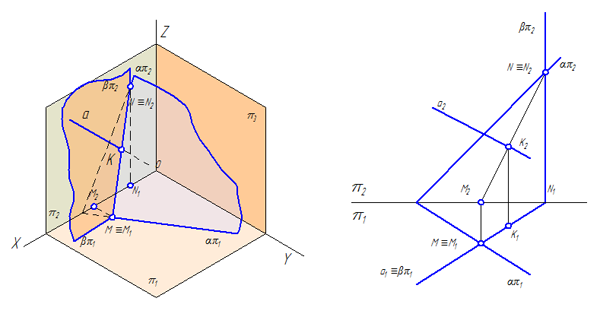
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α
Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.
Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
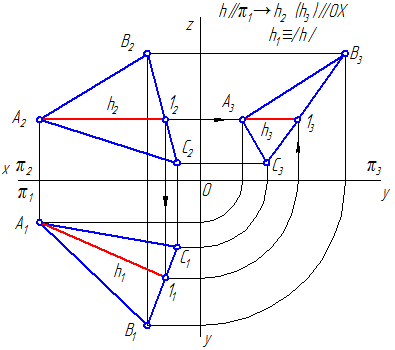
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
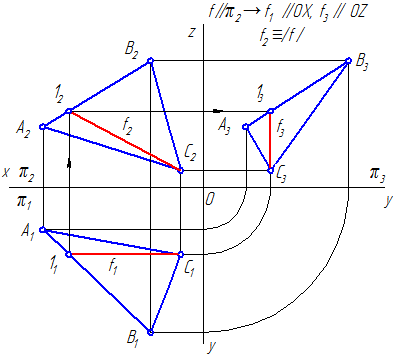
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
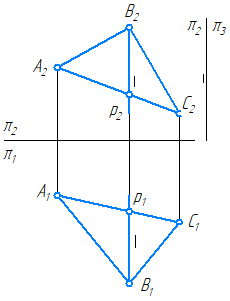
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
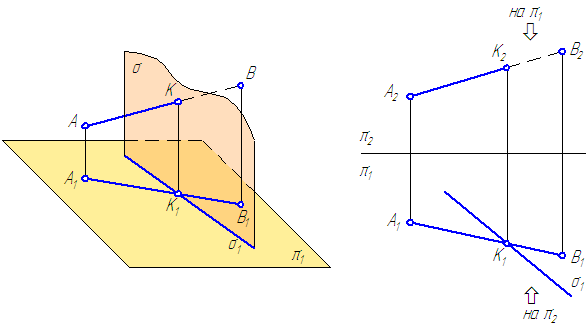
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
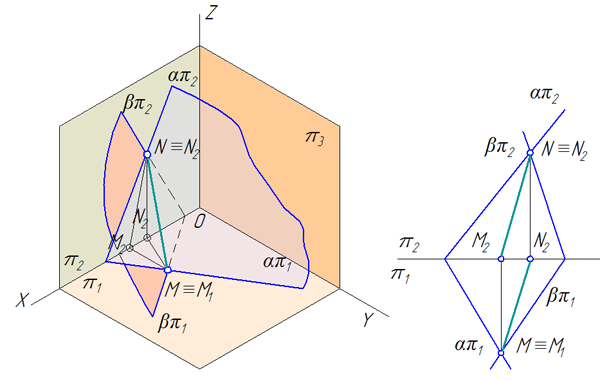
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
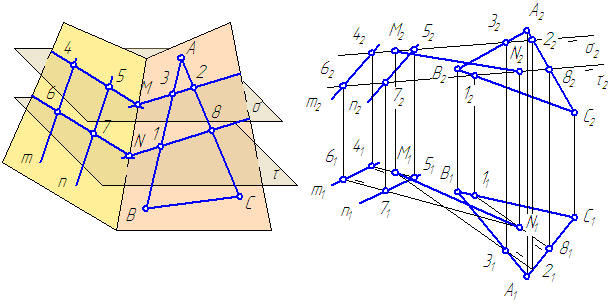
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
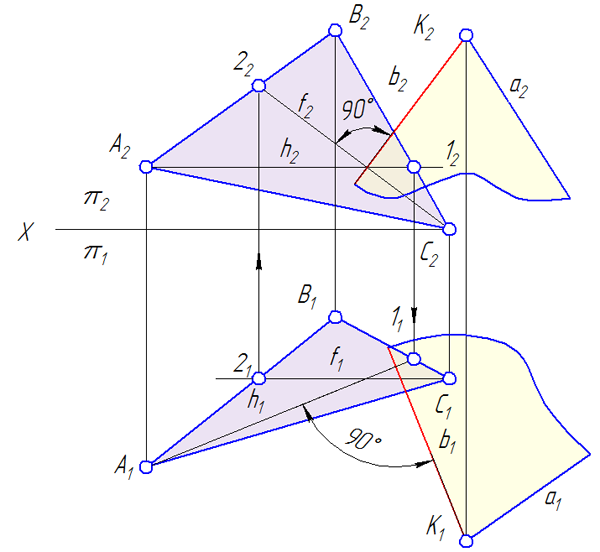
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
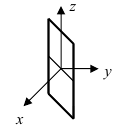
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
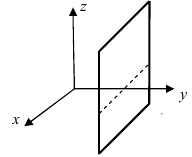
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 — плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
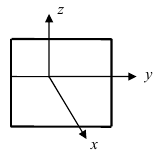
4. 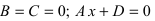
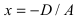
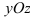
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 — уравнение описывает плоскость 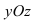
Рис. 40. Координатная плоскость 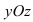
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 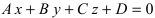
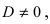
Введем следующие обозначения 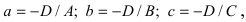
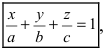
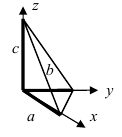
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
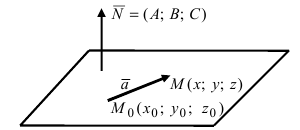
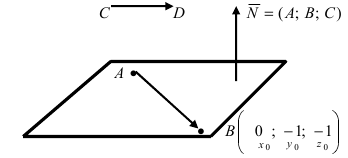
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 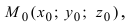
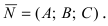
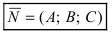
Возьмем на плоскости произвольную точку 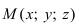
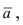
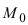
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 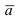
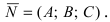
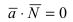
Пример:
Составить уравнение плоскости, проходящей через т. 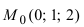
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 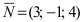
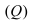
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 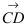
Решение:
Построим на искомой плоскости вектор 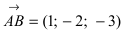
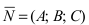
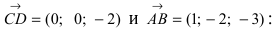
Уравнение плоскости, проходящей через заданную точку 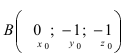
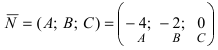
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 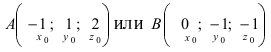
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 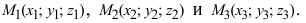
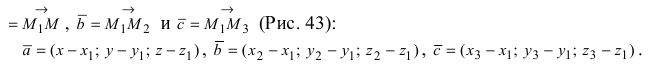
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 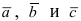
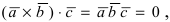
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 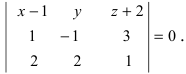
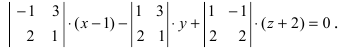
Основные задачи о плоскости в пространстве
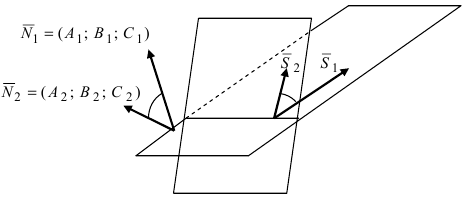
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 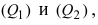
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 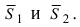
Рис.44. Угол между плоскостями.
В силу того, что 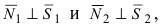
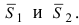
Следствие: Если плоскости перпендикулярны (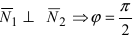
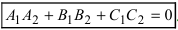
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 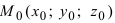
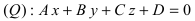
Пример:
На каком расстоянии от плоскости 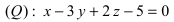
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 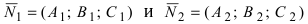
Пусть прямая проходит через точку 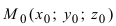
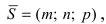
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 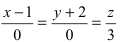
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 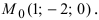
Пример:
Записать уравнение прямой 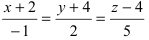
Решение:
Приравняем каждую дробь к параметру t: 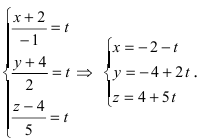
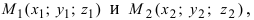
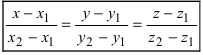
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
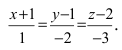
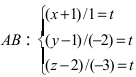
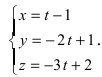
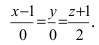
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением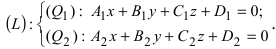
Пример:
Записать уравнение прямой 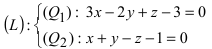
Решение:
Положив х = 0, получим СЛАУ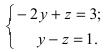
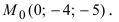
Запишем каноническое 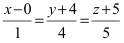
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 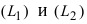
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (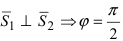
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 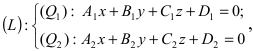
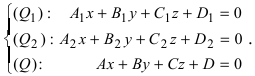
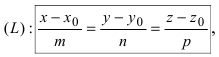
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 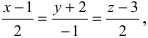
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 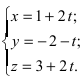
Найденное значение параметра 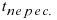
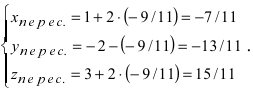
- Заказать решение задач по высшей математике
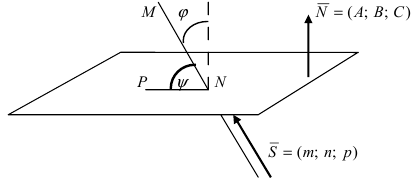
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 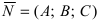
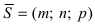
Рис. 45. Угол между прямой и плоскостью.
Угол 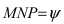
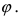
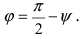
Следствие: Если прямая перпендикулярна плоскости (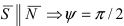
Следствие: Если прямая параллельна плоскости (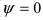
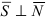
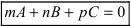
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 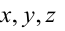

Вектор 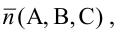
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 — плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 — плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 — плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 — плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 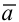
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 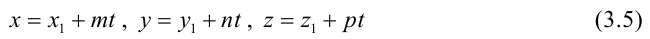
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 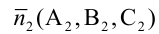
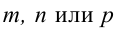
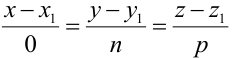
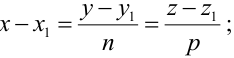
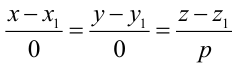
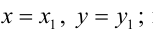
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 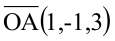
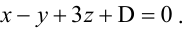
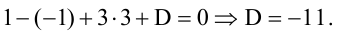
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением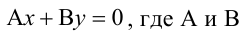
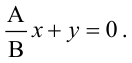
Решая квадратное уравнение 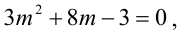
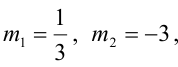
Пример:
Составьте канонические уравнения прямой: 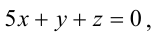
Решение:
Канонические уравнения прямой имеют вид:
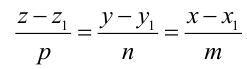
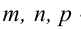
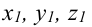
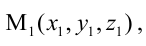
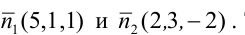
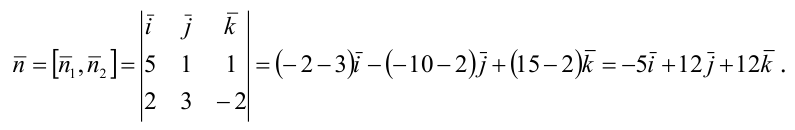
Пример:
В пучке, определяемом плоскостями 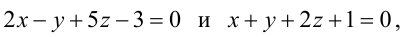
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 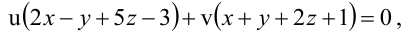
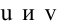
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 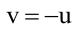
Т.к. и 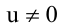
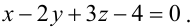
Значит, уравнение второй плоскости имеет вид: 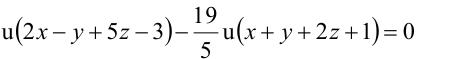
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
Прямая
принадлежит плоскости в том случае,
если эта прямая:
а/
имеет с плоскостью две общие и
нетождественные точки,
б/
имеет с плоскостью одну общую точку
и
эта прямая параллельна другой прямой,
принадлежащей этой п
лоскости.
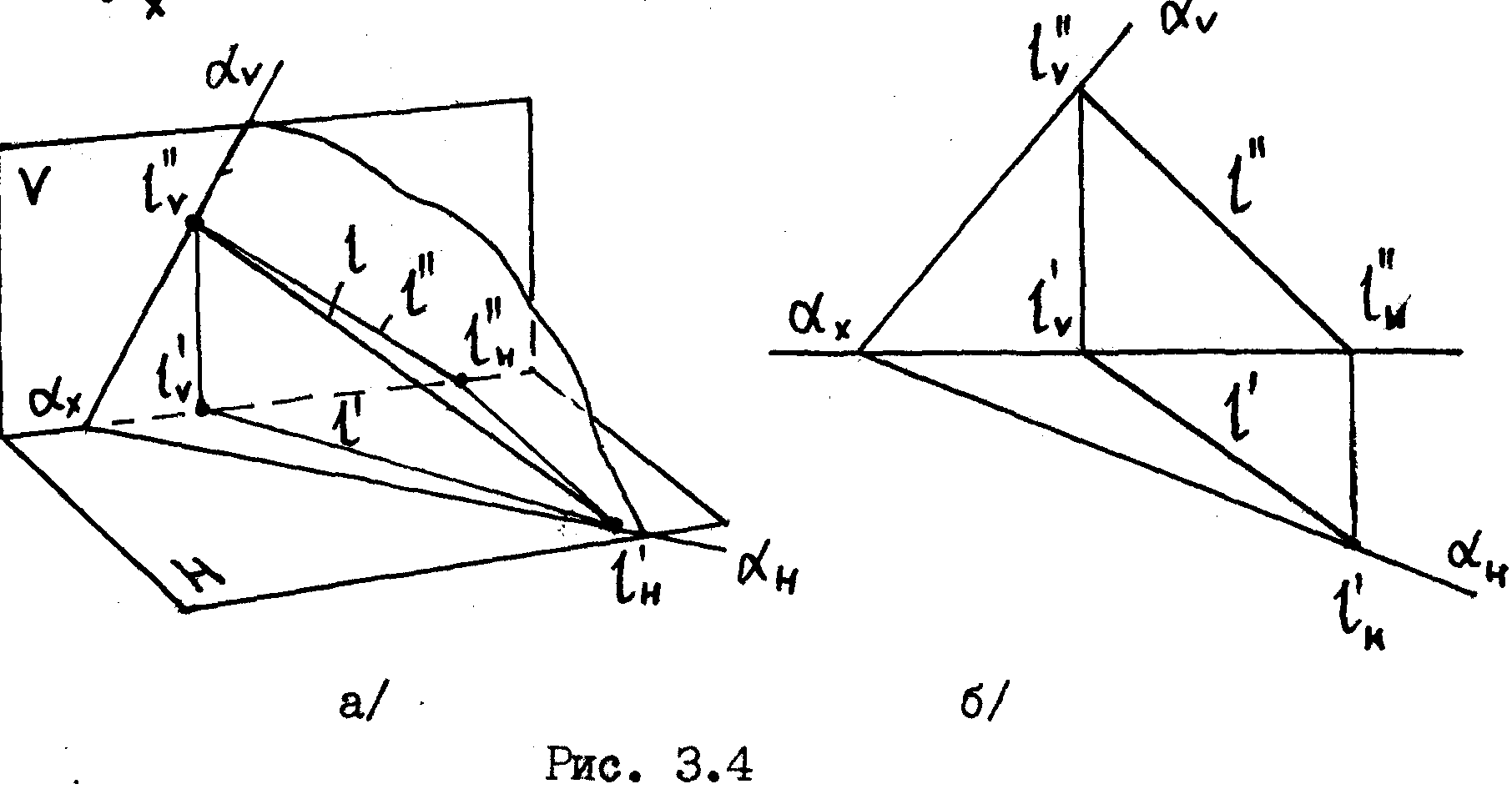
Примеры.
Плоскость
задана пересекающимися прямыми а
и b/рис.3.2/
Прямая
l
принадлежит плоскости»
т.к. имеет с ней две
общие
точки А
и
В
/рис.3.2а/,
Прямая
m
принадлежит
плоскости
,
т.к. имеет с ней общую
точку
К
и
эта прямая параллельна прямой С,
принадлежащей пло-
3.3
скости
/рис.3.26/.
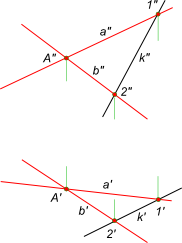
Прямая
n
принадлежит плоскости
,
т.к. имеет с ней общую точку Е
и эта прямая параллельна прямой а
/рис.З.Зв/.
3.3 Принадлежность точки плоскости.
Точка
принадлежит плоскости в том случае,
если она лежит на прямой, принадлежащей
этой плоскости.
Пример
Дана
фронтальная проекция точки М.
Построить горизонтальную проекцию этой
точки, если известно, что точка М
принадлежит плоскости треугольника
АВС/рис.3.3/.
Положение
точки М
можно
определить с помощью любой прямой,
проходящей через точку М
и принадлежащей плоскости треугольника.
В нашем примере в качестве такой прямой
взята прямая АМ.
3.4
Следы плоскости.
Следами
плоскости называются линии пересечения
данной плоскости с плоскостями проекций.
На
рис.3.4 приведено наглядное изображение
плоскости,
заданной следами /рис.3.4а/ и её изображение
на комплексном чертеже /рис.3.4б/.
н
—
горизонтальный след плоскости
,
3.4
v
-фронтальный след плоскости
x
-точка схода следов плоскости
Задание
плоскости следами, по своей сути, является
обычным заданием плоскости пересекающимися
прямыми. Но, в данном случае, это не
случайные, а такие прямые, которые,
помимо данной плоскости, принадлежат
еще и плоскостям проекций.
В
начертательной геометрии охотно
пользуются заданием
плоскости её следами,
т,к. такое задание
а/
обладает, по сравнению с другими
способами, большей наглядностью,
т.к. по расположению следов на эпюре
легко судить и о расположении самой
плоскости в пространстве,
б/
наиболее рационально,
т.к. требует для задания плоскости
построения всего двух прямых.
Обратить
внимание на особенности
задания плоскости следами.
а/
Следы плоскости выполняются тонкими
сплошными линиями,
такими
же,
как линии связи и оси проекций.
б/
На чертеже даются обозначения самих
следов, а их
проекции,
одна из которых совпадает
с самим следом,
а другая — с
осью проекций,
не обозначаются.
в/Следы
обозначаются той же буквой, что и сама
плоскость,
с добавлением индекса той плоскости
проекций, которой этот след принадлежит.
Принадлежность
прямой плоскости, заданной следами,
может быть определена следующим образом.
!Прямая
принадлежит плоскости в том случае,
если следы этой прямой принадлежат
одноименным следам данной плоскости.
3.5
Это
правило легко устанавливается из
рассмотрения рис.3.4.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Принадлежность прямой плоскости
Принадлежность прямой плоскости на комплексном чертеже определяется согласно аксиомам инцидентности или отношения принадлежности между элементами евклидова пространства, которые гласят:
— если точка A принадлежит прямой k, а прямая k принадлежит плоскости α, то точка A принадлежит плоскости α;
— если две точки A и B, принадлежащие прямой k, принадлежат плоскости α, то и прямая k принадлежит плоскости α.
Задача на принадлежность прямой плоскости может быть выражена следующим образом:
— заключить прямую k(k`, k») в;
— провести через прямую k(k`, k»)
плоскость α общего положения
Принадлежность прямой плоскости
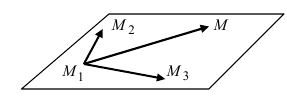
Положение плоскости α в пространстве определяется тремя точками:
— точка A ∉ k;
— точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k.
Проведя прямые через точки 1 и A и 2 и A получим искомую плоскость , заданную пересекающимися прямыми a и b соответственно.
Принадлежность прямой плоскости
Положение плоскости α в пространстве определяется двумя параллельными прямыми:
— a // b и точки 1 ∈ a и 2 ∈ b
— точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k.
Проведя прямые a // b через точки 1 и 2 соответственно получим искомую плоскость , заданную прямыми a // b.
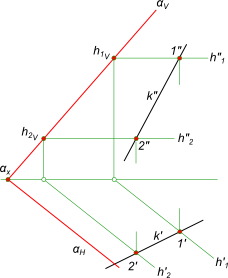
Провести через прямую k(k`, k») плоскость α общего положения, заданную следами
Принадлежность прямой плоскости
Положение плоскости α в пространстве определяется двумя параллельными прямыми — горизонталями плоскости:
— h1 // h2 и точки 1 ∈ h1 и 2 ∈ h2
— точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k.
Проведя прямые h1 // h2 через точки 1 и 2 соответственно, получим искомую плоскость α, заданную следами αH и αV.
+
Взаимное расположение прямой и плоскости в пространстве
Содержание:
-
Понятие плоскости и ее обозначения
- Понятие плоскости
- Обозначение плоскости
-
Как выяснить взаимное расположение прямой и плоскости
- Прямая пересекает плоскость
- Прямая принадлежит плоскости
- Прямая параллельна плоскости
- Различные способы задания прямой на плоскости
- Как найти угол между прямой и плоскостью
Понятие плоскости и ее обозначения
Понятие плоскости
Плоскости окружают нас со всех сторон. Примеры плоских поверхностей: стол, стены, пол и потолок, школьная доска, скамейка, экран, грани карандаша. Плоскость — одно из важнейших понятий геометрии и стереометрии, математики давно пытаются дать ее точное определение.
Евклид (III век до н. э.): «Поверхность есть то, что имеет только длину и ширину», «плоская поверхность есть та, которая одинаково расположена относительно прямых линий, на ней лежащих».
Фурье (1768-1830): «Плоскость есть геометрическое место всех прямых, перпендикулярных к данной прямой в данной на ней точке».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Лежандр (1752-1833): «Плоскость — это поверхность, с которой прямая, имея с ней две общие точки, совмещается всеми своими точками, где бы на плоскости ни были взяты эти точки».
Плоскость — это такая поверхность, в которой целиком лежит всякая прямая, соединяющая две любые точки этой поверхности.
Обозначение плоскости
Невозможно изобразить объект, бесконечно простирающийся в длину и ширину. Поэтому для плоскости приняты условные обозначения. На рисунке вместо плоскости изображают ее часть: параллелограмм или «облако» — овал, область с неровными краями.
Плоскость обозначают строчными буквами греческого алфавита: α (альфа), β (бета), γ (гамма) и т.д.
Как выяснить взаимное расположение прямой и плоскости
Есть три варианта взаимного расположения прямой и плоскости в пространстве:
- Прямая и плоскость пересекаются.
- Прямая принадлежит плоскости (лежит в ней).
- Прямая и плоскость параллельны.
Рассмотрим каждый вариант подробней.
Прямая пересекает плоскость
Прямая и плоскость пересекаются, если они имеют только одну общую точку.
Прямая принадлежит плоскости
Прямая принадлежит плоскости (лежит в плоскости), если все точки прямой лежат в плоскости. При этом достаточно, чтобы две любые точки данной прямой лежали в данной плоскости.
Аксиома 1
Все точки прямой лежат в плоскости, если хотя бы две точки данной прямой лежат в данной плоскости.
Прямая параллельна плоскости
Прямая, не лежащая в плоскости, пересекается с плоскостью или параллельна ей. Прямая и плоскость параллельны, если они не имеют общих точек. Отсутствие общих точек — признак параллельности прямой и плоскости.
Теорема 1
Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости.
Различные способы задания прямой на плоскости
Положение прямой определяют:
- Две заданные точки. Через две точки можно провести только одну прямую. Поэтому координаты точек в прямоугольной системе координат задают отрезок или прямую.
- Точка, через которую она проходит, и параллельная прямая.
- Точка и направляющий вектор.
- Точка и перпендикулярная прямая.
Как найти угол между прямой и плоскостью
Чтобы найти угол между прямой и плоскостью, нужно знать, каков угол между прямой и ее проекцией на эту плоскость.
На изображении прямая АВ пересекает плоскость γ, и является наклонной к этой плоскости. Проведем перпендикуляр АС. ВС — проекция наклонной АВ. Угол между АВ и γ будет равен ∠АВС прямоугольного ΔАСВ.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так






















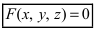
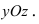
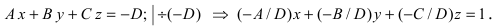
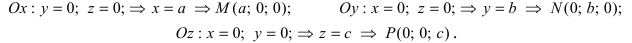
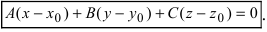
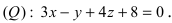
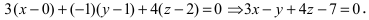
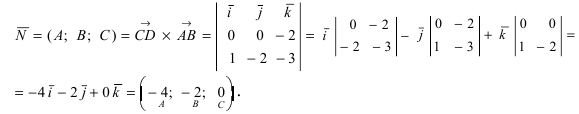
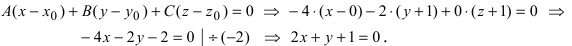

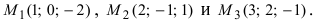
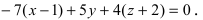
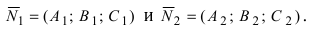
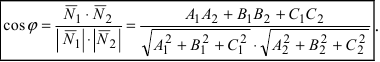
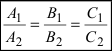
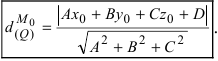
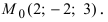
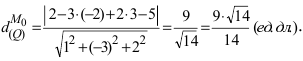
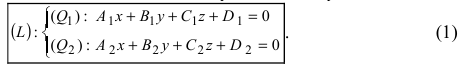
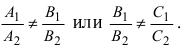

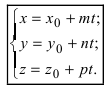
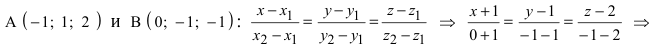
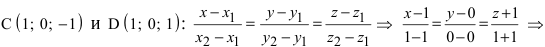
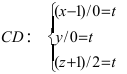
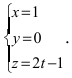

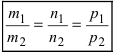
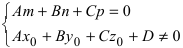 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);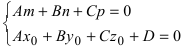 прямая лежит на плоскости;
прямая лежит на плоскости;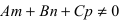 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.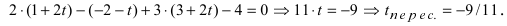
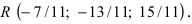
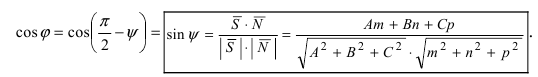
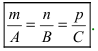
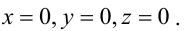
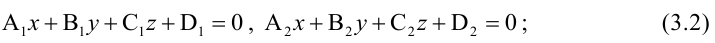
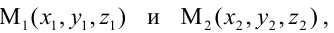 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: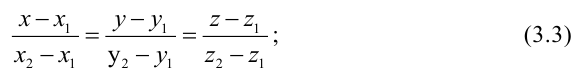
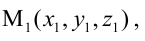 ей принадлежащей, и вектором
ей принадлежащей, и вектором 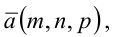 ей коллинеарным.
ей коллинеарным.