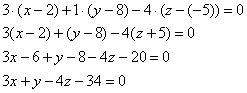Как найти плоскость параллельную данной плоскости



5.3.1. Как найти плоскость, параллельную данной?

Задача 137

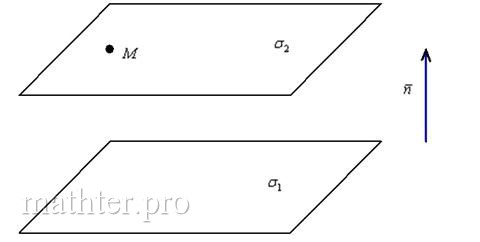
Найти плоскость, проходящую через точку  параллельно плоскости .

Решение: Обозначим известную плоскость через . По условию требуется найти плоскость , которая параллельна плоскости  и проходит через точку .  …Какие есть идеи? Немножко подумайте …

А ещё лучше выполнить схематический чертёж, который сразу поможет с идеей:

У параллельных плоскостей один и тот же вектор нормали. Добавить нечего =) Осталось оформить мат в два хода:

1) Из уравнения  найдём нормальный вектор .

2) Уравнение плоскости  составим по точке  и вектору :

Ответ:

Как выполнить проверку, я уже рассказал.  Продолжаем раскидывать стог сена пространственной геометрии:

5.3.2. Как найти расстояние от точки до плоскости?

5.2.4. Как составить уравнение плоскости по точке и вектору нормали?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн

С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения

Пусть задана точка M₀(x₀, y₀, z₀) и уравнение плоскости

Наша задача найти уравнение плоскости, проходящей через точку M₀ и параллельной плоскости (1)(Рис.1).

Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M₀(x₀, y₀, z₀) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M₀(x₀, y₀, z₀) удовлетворяла уравнению плоскости (1):

Решим (2) относительно D:

Подставляя значение D из (3) в (1), получим:

Уравнение (4) можно представить также в следующем виде:

Уравнение (5) является уравнением плоскости, проходящей через точку M₀(x₀, y₀, z₀) и параллельной плоскости (1).

Пример 1.

Найти уравнение плоскости, проходящей через точку M₀(1, −6, 2) и параллельной плоскости :

Решение.

Запишем коэффициенты нормального вектора плоскости (6):

Подставляя координаты точки M₀ и координаты нормального вектора в (3), получим:

Подставляя значения A, B, C, D в уравнение плоскости (1), получим:

Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:

Ответ.

Уравнение плоскости, проходящей через точку M₀(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:

Привет, сегодня поговорим про существование плоскости параллельной данной плоскости, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
существование плоскости параллельной данной плоскости , настоятельно рекомендую прочитать все из категории Стереометрия.

Теорема

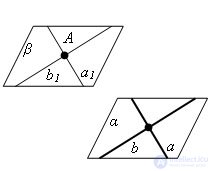
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну. 

Доказательство

Проведем в данной плоскости α какие-нибудь две пересекающиеся прямые a и b . Об этом говорит сайт https://intellect.icu . Через данную точку A проведем параллельные им прямые a1 и b1. Плоскость β, проходящая через прямые a1 и b1, по теореме о признаке параллельности плоскостей параллельна плоскости α. 

Предположим, что через точку A проходит другая плоскость β1, тоже параллельная плоскости α. Отметим на плоскости β1 какую-нибудь точку С, не лежащую в плоскости β. Проведем плоскость γ через точки A, С и какую-нибудь точку B плоскости α. Эта плоскость пересечет плоскости α, β и β1 по прямым b, a и с. Прямые a и с не пересекают прямую b, так как не пересекают плоскость α. Следовательно, они параллельны прямой b. Но в плоскости γ через точку A может проходить только одна прямая, параллельная прямой b. что противоречит предположению. Теорема доказана.

Понравилась статья про существование плоскости параллельной данной плоскости? Откомментируйте её Надеюсь, что теперь ты понял что такое существование плоскости параллельной данной плоскости
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия

Из статьи мы узнали кратко, но емко про существование плоскости параллельной данной плоскости

Плоскости в пространстве

§ 13.Параллельность плоскостей

13.1. Признаки параллельности плоскостей

При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев.

1. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Такие плоскости называются пересекающимися.

2. Две плоскости не имеют общей точки.

Определение. Две плоскости, не имеющие общей точки, называются параллельными.

Если плоскости α и β параллельны, то записывают: α ‖ β или β ‖ α. При этом также говорят, что плоскость α параллельна плоскости β или плоскость β параллельна плоскости α.

В п. 9.1 доказано, что в пространстве существуют параллельные плоскости. Но возникает вопрос: как определить, параллельны ли две данные плоскости? Ответить на этот вопрос помогают признаки параллельности двух плоскостей (т. 18, 19 и 24).

Теорема 18 (признак параллельности плоскостей). Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то данные плоскости параллельны.

Дано: α, β, a ⊂ α, b ⊂ α, a ∩ b = M; a ‖ β, b ‖ β (рис. 82).

Доказать: α ‖ β.

Доказательство. Рассуждаем методом от противного. Предположим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой c (см. рис. 82).

В плоскости α расположены прямая c и данные пересекающиеся прямые a и b. Так как из двух пересекающихся прямых не более чем одна может быть параллельна данной прямой, то прямая c пересекает, по крайней мере, одну из прямых a и b. Пусть прямая c пересекает прямую a в некоторой точке K: a ∩ c = K.

Имеем: прямая c, следовательно, и точка K лежат в плоскости β. Значит, прямая a пересекает плоскость β. Это противоречит условию теоремы (a ‖ β).

Также к противоречию с условием теоремы придём, если допустим, что пересекаются прямые c и b или прямая c пересекает обе прямые a и b.

Таким образом, предположив, что плоскости α и β не параллельны, мы пришли к противоречию. Это означает, что предположение неверно. Следовательно, α ‖ β. Теорема доказана. ▼

Теорема 19. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство. Пусть прямые a и b плоскости α пересекаются в точке M, прямые a1 и b1 плоскости β параллельны соответственно прямым a и b (рис. 83). Тогда по признаку параллельности прямой и плоскости имеем:

a ‖ a1, a1 ⊂ β ⇒ a ‖ β; b ‖ b1, b1 ⊂ β ⇒ b ‖ β.

Таким образом, пересекающиеся прямые a и b в плоскости α параллельны плоскости β. По предыдущей теореме плоскости α и β параллельны. Теорема доказана. ▼

Заметим, что доказанная теорема 19 также является признаком параллельности двух плоскостей и может быть доказана независимо от теоремы 18. Самостоятельно докажите теорему 19, не используя теорему 18.

Докажите самостоятельно, что две плоскости, перпендикулярные одной и той же прямой, параллельны.

13.2. Свойства параллельных плоскостей

Теорема 20. Прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.

Дано: α ‖ β, γ ∩ α = a, γ ∩ β = b (рис. 84).

Доказать: a ‖ b.

Доказательство. Прямые a и b лежат в одной плоскости γ. Эти прямые не имеют общей точки, так как плоскости α и β параллельны. Следовательно, прямые a и b параллельны по определению. Теорема доказана. ▼

Теорема 21. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Дано: α ‖ β, a ∩ α = A (рис. 85).

Доказать: a пересекает β.

Доказательство. Выберем в плоскости β любую точку C. Через эту точку и прямую a проведём плоскость γ.

Так как плоскость γ имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости γ прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости β, то точка B является точкой пересечения прямой a и плоскости β. Теорема доказана. ▼

Теорема 22. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

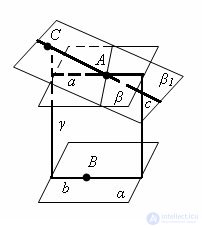
Дано: α ‖ β, α и γ пересекаются (рис. 86).

Доказать: β и γ пересекаются.

Доказательство. Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 21 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана. ▼

Вернёмся к вопросу о существовании параллельных плоскостей.

Теорема 23. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

Дано: α, M; M ∉ α (рис. 87).

Доказать: существует единственная плоскость β такая, что M ∈ β, β ‖ α.

Доказательство. В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании теоремы 19 плоскость β параллельна плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.

Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 22 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана. ▼

Данная теорема даёт способ построения в пространстве плоскости, параллельной данной плоскости.

ЗадаЧа. В кубе ABCDA1B1C1D1 через точку K — середину ребра A1D1 провести сечение, параллельное плоскости A1C1D.

Решение. Плоскость сечения пересекает плоскость AA1D1 по прямой KM, параллельной прямой A1D (почему?), а плоскость DCC1 — по прямой ME, параллельной прямой C1D (почему?). Треугольник KME — искомое сечение (рис. 88).

Самостоятельно постройте сечение этого куба плоскостью, проходящей через середину ребра AA1 параллельно плоскости A1C1D, и вы получите в сечении правильный шестиугольник.

Теорема 24. Две плоскости, параллельные третьей, параллельны.

Дано: α ‖ β, γ ‖ β (рис. 89).

Доказать: α ‖ γ.

Доказательство. Допустим, что плоскости α и γ пересекаются по некоторой прямой c. Выберем на прямой c произвольную точку M. Через эту точку проходят две различные плоскости α и γ, каждая из которых параллельна плоскости β. Это противоречит теореме 23. Значит, предположение было неверно. Поэтому α ‖ γ. Теорема доказана. ▼

Теорема 25. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

Дано: α ‖ β; a ‖ b; a ∩ α = A1, a ∩ β = B1;

b ∩ α = A2, b ∩ β = B2 (рис. 90).

Доказать: A1B1 = A2B2.

Доказательство. Проведём через параллельные прямые a и b плоскость γ (т. 3). Она пересекает параллельные плоскости α и β по параллельным прямым A1A2 и B1B2 (т. 20).

А так как a ‖ b, то четырёхугольник A1A2B2B1 — параллелограмм. Поэтому A1B1 = A2B2 (как противоположные стороны этого параллелограмма). Теорема доказана. ▼

Теорема 26. Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости.

Дано: α1 ‖ α2, l ⊥ α1.

Доказать: l ⊥ α2.

Проведите доказательство самостоятельно, построив две любые плоскости γ1 и γ2, проходящие через прямую l (рис. 91).

 ЗадаЧа 4.007. Построить сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку M основания ABCDE параллельно грани PAB (рис. 92).

Решение. Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани PAB, то: а) прямая пересечения плоскости α с плоскостью ABC (плоскостью основания пирамиды) должна быть параллельна AB; б) прямая пересечения плоскости α с гранью PAE — параллельна AP; в) прямая пересечения α с плоскостью грани PBC — параллельна PB; г) прямая пересечения плоскости α с плоскостью PAD — параллельна PA, поэтому проводим: 1) через точку M прямую KF ‖ AB, K ∈ BC, F ∈ AE; 2) прямую FH ‖ PA, H ∈ PE; 3) прямую KR ‖ PB, R ∈ PC; 4) прямую ML ‖ AP, L ∈ PD. Пятиугольник HLRKF — искомое сечение.

Доказательство проделайте самостоятельно.

Замечание. При внимательном анализе обнаруживается аналогия между свойствами параллельных плоскостей в пространстве и свойствами параллельных прямых на плоскости. Попробуйте, например, пользуясь рисунком 93, сформулировать и доказать «пространственный аналог теоремы Фалеса».

Геометрия, 10 класс

Урок №6. Параллельность плоскостей

Перечень вопросов, рассматриваемых в теме

1. Определение параллельных плоскостей;
2. Свойства параллельных плоскостей;
3. Признак параллельности плоскостей.

Глоссарий по теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Плоскости, которые не пересекаются, называются параллельными.

Основная литература:

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.

Дополнительная литература:

Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24

Теоретический материал для самостоятельного изучения

Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.

Определение. Плоскости, которые не пересекаются, называются параллельными.

Параллельные плоскости α и β обозначаются α∥β.

Изображение:

Пример 1.

Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

Пусть α и β — данные плоскости, a₁ и a₂ – пересекающиеся прямые в плоскости α, а b₁ и b₂ соответственно параллельные им прямые в плоскости β. 

Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.

Прямая a₁ параллельна прямой b₁, значит она параллельна и самой плоскости β.

Прямая a₂ параллельна прямой b₂, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).

 Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a₁ или a₂ пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a₁ или a₂ пересекает плоскость β, чего быть не может, так как прямые a₁ и a₂ параллельны плоскости β.

Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны. 

Теорема доказана.

Свойства параллельных плоскостей.

Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.

Доказательство. 

Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.

Плоскость α пересекается с плоскостью γ по прямой a.  

Плоскость β пересекается с плоскостью γ по прямой b. 

Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.

Доказательство.

Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.

Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.

Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD. 

По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.

Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Доказательство.

Пусть α||β, a пересекает α в точке А.

Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.

Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

Доказательство.

Пусть α||β, α и γ пересекаются.

Докажем, что плоскости β и γ пересекаются.

Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана. 

Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

Доказательство.

Пусть нам даны плоскость α и точка М, ей не принадлежащая.

Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a₁ и b₁, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a₁ и b₁, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку M проходит другая плоскость, например β₁, параллельная α.

Так как β₁ пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β₁ пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана. 

Рассмотрим несколько примеров на применение данных свойств.

Пример 2.

Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.

Доказательство.

Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А₁, эти прямые единственным образом определяют плоскость α.

Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .

Пример 3.

Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.

Доказательство.

Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.

Примеры и разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Три отрезка А₁А₂, В₁В₂ и С₁С₂, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны.

Доказательство.

Докажем параллельность А₁В₁ и А₂В₂.

Рассмотрим плоскость, проходящую через прямые А₁А₂ и В₁В₂

(она существует и единственная, т.к. прямые пересекаются).

В этой плоскости лежит четырехугольник А₁В₁А₂В₂, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А₁В₁ и А₂В₂ параллельны.

Аналогично доказывается параллельность В₁С₁ и В₂С₂. Из вышеперечисленного следует, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны по признаку параллельности плоскостей.

Верное решение:

Докажем параллельность А₁В₁ и А₂В₂.

Рассмотрим плоскость, проходящую через прямые А₁А₂ и В₁В₂

(она существует и единственная, т.к. прямые пересекаются).

В этой плоскости лежит четырехугольник А₁В₁А₂В₂, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А₁В₁ и А₂В₂ параллельны.

Аналогично доказывается параллельность В₁С₁ и В₂С₂. Из вышеперечисленного следует, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны по признаку параллельности плоскостей.

№2.

Тип задания: выделение цветом

Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.

Решение:

Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.

Ответ:

1) они параллельны

2) скрещиваются

3) пересекаются