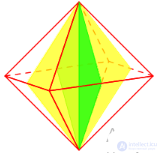
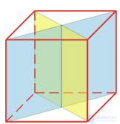
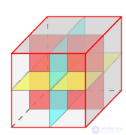
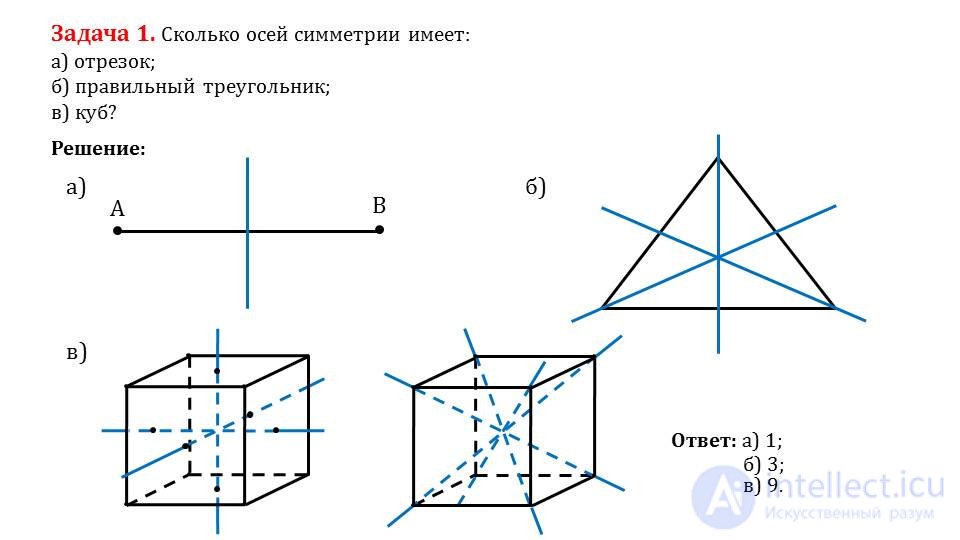
Характеристики гексаэдра (куба)
Число сторон у грани — 4
Общее число граней — 6
Форма грани квадрат
Число рёбер, примыкающих к каждой вершине — 3
Общее число вершин — 8
Общее число ребер — 12
У каждого ребра (красный) имеется три параллельных ребра (синий).
Количество пар параллельных ребер можно определить, умножив общее количество ребер на 3.
В кубе 18 пар параллельных ребер.
У каждого ребра (красный) имеются 8 перпендикулярных ему рёбер (синий). Определить количество пар перпендикулярных ребер можно умножив общее количество рёбер на 8 и разделив на 2.
Всего куб имеет 48 пар перпендикулярных рёбер.
У каждого ребра (красный) имеются 4 скрещивающихся с ним ребра.
Определить количество пар скрещивающихся рёбер можно умножив общее количество рёбер на 4 и разделив на 2.
Всего куб имеет 24 пары скрещивающихся рёбер.
Количество пар параллельных граней — 3
Расстояние между противоположными рёбрами можно определить по формуле
,где а — длина стороны
Длину диагонали куба можно определить по формуле

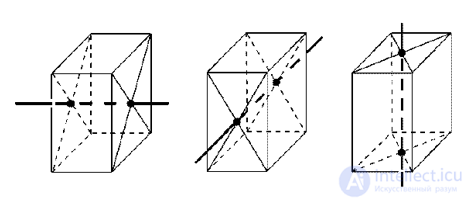
Куб имеет 9 осей симметрии.
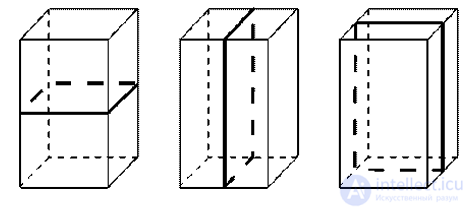
Три оси симметрии это прямые проходящие через центр параллельных граней куба:
Шесть осей симметрии это прямые соединяющие центры противолежащих рёбер куба:
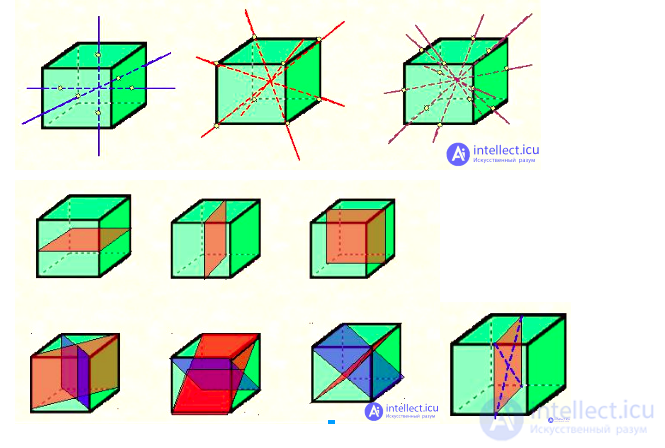
Куб имеет 9 плоскостей симметрии
Три плоскости проходят через центр параллельно граням
Шесть плоскостей проходят через центр по диагонали
Куб может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы куба
где a — длина стороны.
Сфера может быть вписана внутрь куба.
Радиус вписанной сферы куба

Радиус полувписанной сферы можно определить по формуле:
Площадь поверхности куба
Для наглядности площадь поверхности куба можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон куба (это площадь правильного четырехугольника — квадрата) умноженной на 6. Либо воспользоваться формулой:
Объем куба определяется по следующей формуле:
Привет, сегодня поговорим про центральная симметрия параллелепипеда, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников , настоятельно рекомендую прочитать все из категории Стереометрия.
1
симметрия параллелепипеда
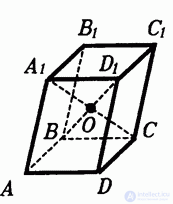
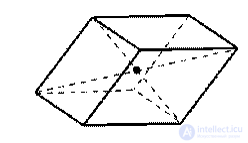
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Поэтому противоположные вершины параллелепипеда симметричны относительно этой точки. Следовательно, каждый параллелепипед имеет центр симметрии — точку пересечения его диагоналей (рис 1.).
В общем случае осей и плоскостей симметрии параллелепипед не имеет, Прямой, но не прямоугольный параллелепипед всегда имеет ось симметрии — прямую, проходящую через центры симметрии его оснований, и плоскость симметрии, проходящую через середины его боковых ребер.
Рисунок 1
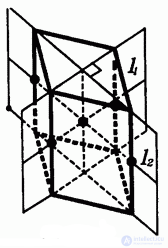
Если основания прямого параллелепипеда — ромбы (но не квадраты), то появляются еще две оси и две плоскости симметрии (Рис 2).
Рисунок 2
Найдите сами элементы симметрии прямоугольного параллелепипеда, среди граней которого нет квадратов.
Если среди граней прямоугольного параллелепипеда есть квадраты, то он является правильной четырехугольной призмой.
Центр симметрии прямоугольного параллелепипеда — точка пересечения диагоналей
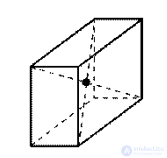
Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер.
Оси симметрии: три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
2 Симметрия в кубе
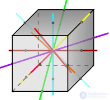
Куб имеет один центр симметрии – точку пересечения его диагоналей. Прямые а и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Обратите внимание, все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии.
Три плоскости симметрии, проходящие через середины параллельных ребер и шесть плоскостей симметрии , проходящие через противолежащие ребра.
3
центральная симметрия параллелепипеда
Теорема
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Доказательство
Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` — параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам.
Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам . Об этом говорит сайт https://intellect.icu . Теорема доказана.
симметрия многогранников
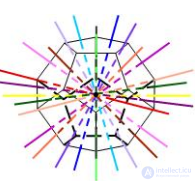
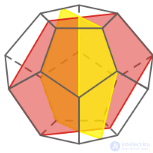
Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника.
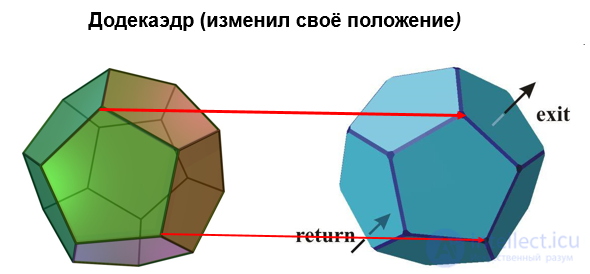
Рисунок Движение додекаэдра
Иначе говоря, под преобразованием симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани. Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении.
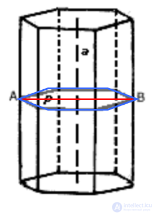
С самым распространенным примером симметрии мы встречаемся в случае прямой правильной n-угольной призмы. Пусть a – прямая, соединяющая центры оснований. Поворот вокруг a на любое целое кратное угла 360/n градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им.
Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия.
Риунок 10
Таблица 1 — Элементы симметрии правильных многогранников
|
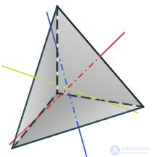
Тетраэдр |
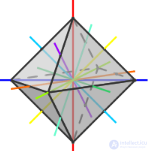
Октаэдр |
Икосаэдр |
Гексаэдр (куб) |
Додекаэдр |
|
| Количество граней | 4 | 8 | 20 | 6 | 12 |
| количество ребер | 6 | 12 | 30 | 12 | 30 |
| вершин | 4 | 6 | 12 | 8 | 20 |
| Центры симметрии | — | 1 | 1 | 1 | 1 |
| Оси симметрии | 3 | 9 | 15 | 9 | 15 |
 |
 |
 |
 |
 |
|
| Порскости симметрии | 6 | 9 | 15 | 9 | 15 |
 |
|
 |
|
 |
|
| Развертки | 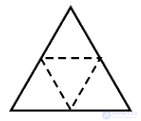 |
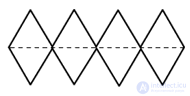 |
 |
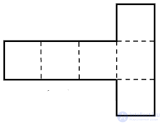 |
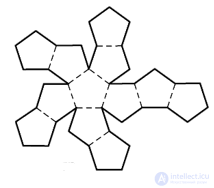 |
Теорема Эйлера Вершины + Грани — Ребра = 2.
Следующий серьезный шаг в науке о многогранниках был сделан в XVIII веке Леонардом Эйлером (1707-1783), который без преувеличения «проверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/n градусов вокруг прямой a есть произведение отражений относительно любых двух плоскостей, содержащих a и образующих относительно друг друга угол в 180/n градусов. (см. рис 10).
Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.
Рисунок 11
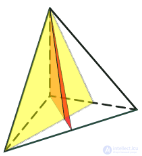
Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра.
Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии.
Задачи .
Сколько осей симметрии имеет отрезок, правильный треугольник, куб?
Тест «Правильные многогранники»
1. Сколько существует видов правильных многогранников?
- 13
- 5
- 4
- Много
2. Какие правильные многогранники имеют по 15 осей симметрии и 15 плоскостей симметрии? (несколько ответов)
- Тетраэдр
- Икосаэдр
- Додекаэдр
- Октаэдр
3. Какой из математиков установил соотношения между числом вершин, ребер и граней выпуклого многогранника?
- Платон
- Архимед
- Эйлер
- Кеплер
4. Согласно теории о связи структуры Земли с правильными многогранниками, проекции каких вписанных в земной шар фигур проступают в земной коре? (несколько ответов)
- Икосаэдр
- Гексаэдр
- Додекаэдр
- Октаэдр
5. Кто автор философской картины мира, где главную роль играют правильные многогранники?
- Эйлер
- Кеплер
- Архимед
- Платон
Вау!! 😲 Ты еще не читал? Это зря!
- понятие симметрии , виды симметрии ,
- симметрия шара , симметрия сферы ,
- симметрии в призме , симметрии в пирамиде ,
- свойство симметрии относительно точки ,
- симметрия относительно прямой , ось симметрии ,
- симметрия относительно точки , центр симметрии ,
- архимедовы тела ,
- тела кеплера — пуансона ,
- многогранники , классификация многогранников ,
- Симметрии в физике
- Суперсимметрия
- Трансляционная симметрия
- Симметрии в биологии
- Асимметрия
- диссимметрии
- сферическая симметрия
- аксиальная симметрия
- радиальная симметрия
- трансляционная симметрия
- двусторонняя (билатеральная) симметрия
- Симметрия в химии
- Анизотропия
- Симметрия в религии и культуре
Понравилась статья про центральная симметрия параллелепипеда? Откомментируйте её Надеюсь, что теперь ты понял что такое центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия
2.О симметриях правильных многогранников
2.1.О самосовмещениях фигуры
Ранее были рассмотрены фигуры (куб, правильная пирамида и др.), имеющие центр (ось, плоскость) симметрии. Каждая из этих фигур при симметрии относительно точки (прямой, плоскости) отображается на себя. В таком случае говорят, что при данной симметрии фигура Ф самосовмещается (совмещается сама с собой), а преобразование симметрии при этом называют самосовмещением фигуры Ф.
Вместе с тем, кроме упомянутых симметрий, существуют другие виды движений, а также композиции таких движений, при которых происходят самосовмещения данной фигуры. Например, повороты на углы 90, 180, 270 и 360° вокруг прямой, проходящей через центры параллельных граней куба, являются самосовмещениями этого куба (рис. 234). Можно убедиться, что различные композиции этих поворотов также являются самосовмещениями данного куба.
Рис. 234
Рис. 235
Самосовмещениями правильной треугольной пирамиды (рис. 235) являются такие движения пространства, как, например, повороты на углы 120, 240 и 360° вокруг прямой, содержащей высоту пирамиды, а также симметрия относительно плоскости, проходящей через эту высоту и боковое ребро. Композиции этих поворотов и плоскостных симметрий также являются самосовмещениями данной пирамиды.
Самосовмещениями правильного тетраэдра являются, например, такие движения пространства, как повороты на углы 120, 240 и 360° вокруг прямой, содержащей высоту этого тетраэдра, а также повороты на угол 180° вокруг прямых, проходящих через середины его скрещивающихся рёбер. Можно убедиться, что композиция любых двух из этих движений также является самосовмещением правильного тетраэдра.
Для движений пространства, самосовмещающих данную фигуру Ф, имеет место следующая теорема.
Теорема 1 (теорема о самосовмещениях фигуры).1. Если два движения пространства являются самосовмещениями фигуры Ф, то их композиция (в любом порядке) является также самосовмещением этой фигуры. 2. Если движение g является самосовмещением фигуры Ф, то обратное ему движение g–1 является также самосовмещением этой фигуры. 3. Тождественное преобразование Е пространства является самосовмещением любой фигуры.
Докажите эту теорему самостоятельно.
Как видно из приведённых выше примеров с кубом, правильной пирамидой и правильным тетраэдром, фигура Ф может иметь не единственное, а несколько самосовмещений. Множество всех самосовмещений фигуры Ф называют группой самосовмещений или группой симметрий этой фигуры.

Так что же собой представляет абстрактное понятие «группа»?
Предварительно рассмотрим следующий вопрос.
Пусть G — множество любых элементов (этим множеством может быть, например, множество Z всех целых чисел, множество Q всех рациональных чисел, множество R всех действительных чисел; а может быть и не числовое множество, например, множество всех преобразований плоскости или множество всех преобразований пространства). Если любым двум элементам а и b множества G ставится в соответствие по определённому правилу некоторый элемент с этого же множества G, то говорят, что на множестве G задана операция (точнее, бинарная операция: от лат. binarius — двойной) или множество G замкнуто относительно этой операции.
На числовых множествах такими операциями могут быть, например, операция сложения (которая обозначается символом «+», и тогда каждым двум числам a и b соответствует их сумма a + b) или операция умножения (которая обозначается символом «•», и тогда каждым двум числам a и b соответствует их произведение a•b).
Если G — множество всех преобразований пространства, то на этом множестве нами в п. 2.3 главы 1 была также определена операция — последовательное применение преобразований, которая обозначается символом «∘». Согласно этой операции любым двум преобразованиям g1 и g2 пространства соответствует их композиция g2 ∘ g1. Иногда композицию g2 ∘ g1 преобразований g1 и g2 называют произведением этих преобразований.
Бинарную операцию, которую вводят на множестве G, можно обозначать любым отвлечённым символом, например символом «*». Согласно вышесказанному, символ «*» принимает конкретный смысл: «+» — сложение чисел, «•» — умножение чисел, «∘» — последовательное применение преобразований.
Теперь введём определение понятия группы.
Определение. Непустое множество G элементов а, b, с, …, на котором определена операция «*», называется группой (относительно этой операции), если для любых элементов а, b, с, … множества G выполняются следующие условия: 1) a * (b * с) = (а * b) * с (т. е. операция «*» ассоциативна); 2) во множестве G существует такой элемент e, что для любого элемента a этого множества выполняется равенство: е * а = а * e = а (элемент е называют нейтральным элементом группы); 3) для любого элемента a множества G существует такой элемент а–1 этого же множества G, что справедливо равенство а * а–1 = а–1 * а = е (элемент a–1 называется обратным элементу a). Если, кроме того, для любых двух элементов а и b множества G выполняется равенство а * b = b * а (операция «*» коммутативна), то группа G называется коммутативной (или абелевой).
Рассмотрим некоторые примеры.
1) Множество всех целых чисел является группой относительно операции сложения, так как операция сложения целых чисел ассоциативна; роль нейтрального элемента группы играет число 0, а роль обратного элемента для любого целого числа a играет число –a. Но множество Z не является группой относительно операции умножения, так как обратным для любого целого числа a ≠ 1 является число a–1 = 
2) Множество Q всех рациональных чисел является группой относительно операции сложения (роль нейтрального элемента группы играет число 0), а множество Q всех рациональных чисел, отличных от нуля, является группой относительно операции умножения (роль нейтрального элемента группы играет число 1).
3) Множество всех векторов пространства является группой относительно операции сложения векторов (роль нейтрального элемента в группе играет нуль-вектор).
Все эти три группы являются абелевыми, так как операция сложения чисел и операция сложения векторов коммутативны.
4) Множество всех преобразований пространства является группой, так как: определённая на этом множестве операция — композиция преобразований обладает свойством ассоциативности (см. п. 2.3 главы 1); роль нейтрального элемента в группе преобразований играет тождественное преобразование Е (для любого преобразования g имеет место g ∘ E = E ∘ g = g (см. п. 2.2 главы 1)) и, наконец, для любого преобразования g существует обратное ему преобразование g –1 такое, что g ∘ g –1 = g –1 ∘ g = E (см. п. 2.3 главы 1).
5) Множество всех движений пространства является группой, так как композицией двух любых движений пространства является движение этого пространства, а преобразованием, обратным любому движению, является движение, и тождественное преобразование Е является движением, играющим роль нейтрального элемента этой группы.
6) Так как самосовмещения любой фигуры Ф происходят при движениях пространства и различных их композициях, причём композиция движений, а следовательно, и композиция самосовмещений данной фигуры обладает свойством ассоциативности, то с учётом утверждения теоремы 1 приходим к выводу: множество GФ всех самосовмещений любой фигуры Ф является группой, которую называют группой симметрий этой фигуры.
2.2.Об элементах симметрии правильного многогранника. Двойственные правильные многогранники
При сравнении самосовмещений правильного тетраэдра и правильной треугольной пирамиды можно обнаружить, что число различных самосовмещений правильного тетраэдра превосходит число самосовмещений правильной треугольной пирамиды, т. е. правильный тетраэдр «симметричнее» правильной треугольной пирамиды. Аналогично, если рассмотреть самосовмещения куба и любой правильной четырёхугольной призмы, то обнаружится, что куб «симметричнее» правильной четырёхугольной призмы. По-видимому, тем и объясняется тот факт, что правильные многогранники всегда привлекали к себе внимание людей своей «симметричностью», являясь «самыми симметричными» многогранниками из множества всех существующих многогранников.
Так как все самосовмещения любой фигуры образуют группу симметрий этой фигуры, то, естественно, представляет интерес, какие движения пространства образуют группу симметрий каждого из пяти правильных многогранников.
Прежде чем приступать к рассмотрению этого вопроса, введём необходимые в дальнейшем определения некоторых понятий.
Прямая, вокруг которой происходит поворот, самосовмещающий фигуру Ф, называется осью поворотной симметрии фигуры Ф. Например, осью поворотной симметрии правильной треугольной пирамиды (см. рис. 235) является прямая, содержащая высоту пирамиды.
Если самосовмещением фигуры является зеркальный поворот, то ось поворота называется осью зеркально-поворотной симметрии. Например, прямая, проходящая через центры параллельных граней куба (см. рис. 234), является его осью зеркально-поворотных симметрий с углами поворотов 90, 180, 270°; плоскостью симметрии при этом служит плоскость, проходящая через центр куба перпендикулярно оси вращения.
Центр симметрии, плоскость симметрии и оба вида осей симметрии, имеющиеся у фигуры Ф, называются её элементами симметрии. Каждому элементу симметрии фигуры соответствует определённое её самосовмещение — элемент группы симметрии этой фигуры.
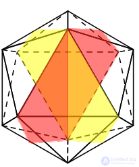
Далее заметим, что число вершин куба равно числу граней правильного октаэдра, а число вершин правильного октаэдра равно числу граней куба. Число рёбер у этих многогранников одно и то же. Поэтому куб и правильный октаэдр называют двойственными многогранниками. Более того, центры граней куба служат вершинами правильного октаэдра (см. задачу 2.348) (рис. 236), а центры граней правильного октаэдра — вершинами куба (см. задачу 2.355) (рис. 237).
Аналогично можно убедиться, что двойственными являются правильный икосаэдр и правильный додекаэдр, при этом центры граней правильного икосаэдра служат вершинами правильного додекаэдра (рис. 238), а центры граней правильного додекаэдра — вершинами правильного икосаэдра (рис. 239).
Рис. 236
Рис. 237
Рис. 238
Рис. 239
Так как любое самосовмещение правильного многогранника является самосовмещением двойственного ему правильного многогранника (почему?), то группы симметрий двойственных правильных многогранников совпадают. Поэтому для изучения групп симметрий каждого из правильных многогранников достаточно рассмотреть группы симметрий правильного тетраэдра, куба и правильного икосаэдра.
2.3.Группа симметрий правильного тетраэдра
Прямая, содержащая высоту ОР правильного тетраэдра РАВС (рис. 240), является осью поворотных симметрий этого тетраэдра с углами поворотов 120, 240° (поворот на угол 360° является тождественным преобразованием). Правильный тетраэдр имеет 4 такие оси поворотных симметрий.
Прямая DE, проходящая через середины D и Е противоположных рёбер СР и АВ правильного тетраэдра РАВС, перпендикулярна каждому из них. Поэтому прямая DE является также осью поворотной симметрии с углом поворота 180°. Правильный тетраэдр имеет 3 такие оси симметрии.
Плоскость, проходящая через ребро правильного тетраэдра и середину противоположного ребра, служит его плоскостью симметрии. Правильный тетраэдр имеет 6 таких плоскостей симметрии.
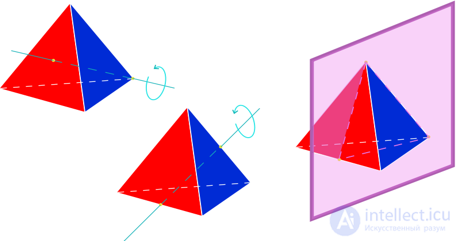
Исследуем вопрос о наличии у правильного тетраэдра оси зеркально-поворотной симметрии. В целях наглядности рассмотрим правильный тетраэдр Т = AB1CD1 вместе с кубом K = АBCDA1B1C1D1 (рис. 241).
Рис. 240
Рис. 241
Пусть a — прямая, проходящая через середины O и O1 противоположных рёбер АС и B1D1 правильного тетраэдра Т; α — плоскость, проходящая через центр М тетраэдра Т (он совпадает с центром куба K) и перпендикулярная прямой a.
При композиции поворота на угол 90° вокруг прямой a и симметрии относительно плоскости α происходит самосовмещение правильного тетраэдра Т. Самосовмещением тетраэдра T является и композиция Sα ∘ 
Таким образом, правильный тетраэдр имеет следующие элементы симметрии: 4 оси поворотных симметрий с углами поворота 120, 240°; 3 оси поворотных симметрий с углами поворота 180°; 3 оси зеркально-поворотных симметрий с углами поворотов 90, 270°; 6 плоскостей симметрии. Учитывая тождественное преобразование, находим, что элементы симметрии правильного тетраэдра определяют
4•2 +3 + 3•2 + 6 + 1 = 24
его симметрии, т. е. группа симметрий правильного тетраэдра состоит из 24 различных самосовмещений. Это число равно удвоенному числу плоских углов тетраэдра.
2.4. Группа симметрий куба
Найдём элементы симметрии куба (правильного гексаэдра).
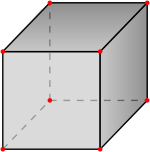
Точка М пересечения диагоналей куба (рис. 242) является его центром и служит центром симметрии этого куба.
Куб имеет 3 плоскости симметрии, каждая из которых проходит через центр куба параллельно его граням, и 6 плоскостей симметрии, каждая из которых проходит через его противоположные рёбра (см. рис. 242).
Прямая ОO1, проходящая через центры О и О1 параллельных граней ABCD и A1B1C1D1 куба (см. рис. 242), является осью поворотных симметрий с углами поворотов 90, 180, 270°. Так как у куба 3 пары параллельных граней, то он имеет 3 такие оси поворотных симметрий.
Прямая РK, проходящая через середины противоположных рёбер куба (см. рис. 242), является осью поворотной симметрии с углом поворота 180°. Куб имеет 6 таких осей симметрии.
Рис. 242
Рис. 243
Рис. 244
Так как треугольники A1BD и B1CD1 — правильные (почему?) (рис. 243) и диагональ AC1 перпендикулярна плоскостям этих треугольников (почему?), то прямая АС1 служит осью поворотных симметрий куба с углами поворотов 120, 240°. Куб имеет 4 такие оси симметрии.
Прямая ОО1 (см. рис. 242) является осью зеркально-поворотных симметрий с углами поворотов 90, 270°, где плоскостью симметрии служит плоскость, проходящая через центр М куба перпендикулярно прямой OO1. Куб имеет 3 такие оси зеркально-поворотных симметрий.
Наконец, пересечением куба и плоскости, проходящей через его центр M перпендикулярно диагонали AC1, является правильный шестиугольник (докажите это, рис. 244). Композиции поворотов на углы 60 и 300° вокруг прямой AC1 и симметрии относительно плоскости этого шестиугольника являются зеркальными поворотами куба. Поэтому прямая АС1 служит осью зеркально-поворотных симметрий куба. Куб имеет 4 такие оси симметрии.
Таким образом, у куба имеются следующие элементы симметрии: 1 центр симметрии; 9 плоскостей симметрии; 3 оси поворотных симметрий, каждая из которых с углами поворотов 90, 180, 270°; 4 оси поворотных симметрий, каждая из которых с углами поворотов 120, 240°; 6 осей поворотных симметрий с углом поворота 180°; 3 оси зеркально-поворотных симметрий (каждая с углами поворотов 90, 270°); 4 оси зеркально-поворотных симметрий (каждая с углами поворотов 60, 300°).
Учитывая тождественное преобразование, находим, что элементы симметрии куба определяют
1 + 9 + 3•3 + 4•2 + 6 + 3•2 + 4•2 + 1 = 48
его симметрий, т. е. группа симметрий куба состоит из 48 различных самосовмещений. Это число равно удвоенному числу плоских углов куба.
2.5.Группа симметрий правильного икосаэдра
Попробуем перечислить все элементы симметрии правильного икосаэдра.
Можно убедиться, что правильный икосаэдр J имеет центр, который является его центром симметрии. Пусть О — центр симметрии правильного икосаэдра J (рис. 245). Это означает, что если точка М1 — вершина икосаэдра J, то на прямой ОМ1 лежит ещё одна его вершина 
Рис. 245
Так как все грани правильного икосаэдра — равные правильные треугольники, то пирамида M1M2M3M4M5M6 является правильной пятиугольной. Поэтому прямая M1O проходит через центр основания этой пирамиды и служит её осью вращения, а следовательно, осью поворотных симметрий икосаэдра J с углами поворотов 
Пусть O1 — центр правильного треугольника М1M4M5 (см. рис. 245), являющегося гранью икосаэдра J. Тогда правильный треугольник 


Кроме того, правильный икосаэдр имеет 15 осей поворотных симметрий с углом поворота 180°, каждая из которых проходит через середины двух его рёбер, симметричных относительно центра O.
Плоскость, проходящая через центр О икосаэдра J перпендикулярно одной из его осей симметрии, является плоскостью симметрии этого икосаэдра. Правильный икосаэдр имеет 15 таких плоскостей симметрии.
Учитывая тождественное преобразование, находим, что элементы симметрии правильного икосаэдра определяют
1 + 6•4 + 6•4 + 10•2 + 10•2 + 15 + 15 + 1 = 120
его симметрий, т. е. группа симметрий правильного икосаэдра состоит из 120 самосовмещений. Это число равно удвоенному числу плоских углов правильного икосаэдра.
Так как правильный октаэдр двойствен кубу, а правильный додекаэдр — икосаэдру, то группа симметрий правильного октаэдра содержит 48 самосовмещений, а группа симметрий правильного додекаэдра — 120 самосовмещений. Число 120 вдвое больше числа плоских углов додекаэдра, а число 48 вдвое больше числа плоских углов правильного октаэдра.
Оказывается, справедлива следующая теорема, которую примем без доказательства.
Теорема. Число элементов группы симметрий правильного многогранника равно удвоенному числу его плоских углов.

|
Куб
Самый популярный многогранник из семейства Платоновых тел. |
Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма плоских углов
при каждой вершине равна 270°.
У куба 12 ребер, имеющих равную длину. Примем длину ребра куба за а и представим числовые характеристики его элементов.
| Сумма длин всех ребер | 12а |
|
| Площадь поверхности | 6а2 | |
| Объем | V = а3 | |
| Радиус описанной сферы |
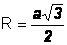
|
|
| Радиус вписанной сферы | r = a/2 |
Кубу свойственны все виды симметрии.
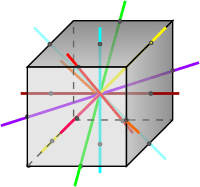
|
Центром симметрии является точка пересечения диагоналей куба. Через центр симметрии проходят 9 осей симметрии. Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через |
|
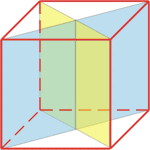
|
Плоскостей симметрии у куба также 9 и проходят они либо через противоположные |
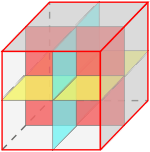
|
В мире нет места для некрасивой математики.
Готфрид Харди
Правильные многогранники — самые выгодные фигуры. И природа этим широко пользуется.
Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников.
Куб передает форму кристаллов поваренной соли NaCl.
Форму куба имеют кристаллические решётки многих металлов (Li, Na, Cr, Pb, Al, Au, и другие), кристалл алмаза, кристаллическая решётка
хлорида цезия CsCl.
В 2009 г. должно исполниться 500 лет со времени выхода в свет книги Луки Пачоли «Божественная пропорция»,
а следовательно, и изобретения Леонардо да Винчи для ее иллюстрации метода жестких ребер.
Леонардо изображал своим способом не только индивидуальные многогранники, но и, например, плотную упаковку кубов.
Этим изображением Леонардо на три века предвосхитил гипотезу о периодическом строении кристаллов, высказанную французскими
кристаллографами аббатом Рэнэ-Жюстом Гаюи (1743-1822) и морским офицером Огюстом Бравэ (1811-1863).


Можно сравнить этот рисунок Леонардо с похожей работой Маурица Эшера, относящейся к 1952 г., «Ячейки кубического пространства».
Не менее интересна другая работа Маурица Эшера.
В центре гравюры «Водопад» расположен комплекс конструкций, поднимающийся на фоне ландшафта с террасами.
Вертикальная ось создается двумя мощными башнями, каждая из которых увенчана острогранными многогранниками
слева — три пересекающиеся куба, а справа также три пересекающихся правильных октаэдра.
Маленькие домики примыкают к башням слева и справа в едином комплексе. Слева на первом плане картины изображен
маленький садик со странными, необычными подводными растениями. Центральным действием картины является ручей, который
падает на колесо и крутит его. Он течет слегка полого вниз и извивается, проходя через башни, при этом он трижды протекает
через точку, в которой уже проходил. Абсурдность доходит до нас через круг неправильных соединений куба.
В результате невольного восприятия зрительная точка оказывается самой ближней, а самая высокая точка становится самой низкой.
Водопад на картине Маурица Эшера осуществляет то,что мы считаем невозможным — вечное движение.
Тема: Симметрия в
кубе, в параллелепипеде, в призме и в пирамиде. Представление о правильных
многогранниках.
Цель:проверить в ходе занятия усвоение знаний
Предметные:геометрическое тело и
поверхность, многогранники: призма, пирамида, параллелепипед, правильные
многогранники, площадь полной и боковой поверхности многогранников.
Метапредметные: развивать логическое мышление и пространственное воображение при
построении геометрических тел и их элементов, умение
анализировать, сравнивать, делать выводы относительно площади пространственных
тел и их поверхностей.
Личностные: воспитывать познавательный интерес, внимательность при
построении пространственных тел, культуру труда, дисциплинированность на занятие.
I. Проверка знаний студентов. Тест по теме
«Многогранники и их основные свойства» (15 мин.)
II. Изучение нового материала.
План:
1) Симметрия:
определение и основные понятия.
2) Симметрия
в кубе.
3) Симметрия
в параллелепипеде.
4) Симметрия
в призме.
5) Симметрия
в пирамиде.
6) Представление
о правильных многогранниках.
(1) Однажды
Л.Н. Толстой сказал: «Стоя перед чёрной доской и рисуя на ней мелом разные
фигуры, я вдруг был поражён мыслью: почему симметрия приятна глазу? Что такое
симметрия? Это врождённое чувство. На чём же оно основано?».
? Как вы понимаете, что такое симметрия? Где мы
можем встретиться с симметрией? Приведите примеры симметрии в природе,
технике, архитектуре, быту.
Совершенно
верно. С симметрией мы встречаемся в природе, архитектуре, технике, быту. Мы
часто видим симметричные творения природы (листья, цветы, птицы, животные) или
творения человека (здания, техника) — все то, что окружает нас каждый день. В
быту: молотки, рубанки, лопаты, трубы. Мы смотрим на себя в зеркало и видим,
что части нашего лица симметричны друг другу. По улицам ездят автомобили,
автобусы, правая и левая части которых симметричны. Таким образом, симметрия
бывает не только на плоскости (кленовый лист), но и в пространстве (лицо).
В школьном курсе
геометрии вы изучали симметрию на плоскости. А сегодня на уроке мы рассмотрим с
вами симметрию в пространстве. Ни одно геометрическое
тело не обладают таким совершенством и красотой, как многогранник.
«Многогранников вызывающе мало, — написал когда-то Л. Кэролл, — но этот
весьма скромный по численности отряд сумел пробраться в самые глубины
различных наук».
«Симметрия» в переводе с греческого означает «соразмерность»
(повторяемость). Симметричные тела и предметы состоят из
равнозначных, правильно повторяющихся в пространстве частей. Особенно
разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или
меньшей симметричностью. Она является их важнейшим и специфическим свойством,
отражающим закономерность внутреннего строения.
Симметрия – это
закономерная повторяемость элементов (или частей) фигуры или какого-либо тела,
при которой фигура совмещается сама с собой при некоторых преобразованиях
(вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр
симметрии и плоскость симметрии.
1) Ось симметрии — воображаемая
ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с
собой в пространстве (
2) Центр симметрии — это точка
внутри многогранника, в которой пересекаются и делятся пополам прямые,
соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит
многогранник на 2 зеркально равные части (Р).
4) Степенью симметрии называется
совокупность всех элементов симметрии, которыми обладает данный многогранник. Например,
куб обладает высокой степенью симметрии, т.к. в нём присутствуют 3 оси
симметрии четвёртого порядка (3, четыре оси симметрии 3 — го порядка (4
, шесть
осей второго порядка (6 В точке пресечения осей симметрии
располагается центр симметрии куба. Кроме того в кубе можно провести 9
плоскостей симметрии (9Р).

Кубу
свойственны все виды симметрии.
а) Центр симметрии (центр куба) — точка
пресечения диагоналей куба.
б) Плоскости симметрии (9): 1) 3 плоскости
симметрии, проходящие через середины параллельных ребер; 2) 6 плоскостей
симметрии, проходящие через противолежащие ребра.
в) Оси симметрии (13): 1) 3 оси,
проходящие через центры противолежащих граней; 2) 4 оси симметрии, проходящие
через противолежащие вершины; 3) 6 осей, проходящие через середины противолежащих
рёбер.
(3) Симметрия в параллелепипеде.
а) Центр симметрии — точка пересечения
диагоналей прямоугольного параллелепипеда.
б) Плоскость симметрии. 3 плоскости
симметрии, проходящие через середины параллельных рёбер.
в) Оси симметрии. 3 оси симметрии,
проходящие через точки пересечения диагоналей противолежащих граней
(4) Симметрия в призме.
1) Симметрия прямой призмы. Одна плоскость
симметрии, проходящая через середины боковых рёбер.
2) Симметрия правильной призмы.
а) Центр симметрии. При чётном числе
сторон основания центр симметрии — это точка пересечения диагоналей правильной
призмы.
б) Плоскости симметрии: 1) плоскость,
проходящая через середины боковых рёбер; 2) при чётном числе сторон основания —
плоскости, проходящие через противолежащие рёбра.

в)
Ось симметрии: а) при чётном числе сторон основания — ось симметрии
проходит через центры оснований; б) оси симметрии, проходящие через точки
пресечения диагоналей противолежащих боковых граней.
(5) Симметрия в пирамиде.
а) Плоскости симметрии: при четном
числе сторон основания — а) плоскости, проходящие через противолежащие боковые
ребра, и б) плоскости, проходящие через медианы, проведенные к основанию
противолежащих боковых граней.

четном числе сторон основания — ось симметрии проходит через вершину
правильной пирамиды и центр основания.
(6) Самостоятельная работа студентов по теме »
Представление о правильных многогранниках». Задание: заполнить
таблицу «Правильные многогранники».
|
Определение правильного |
Изображение |
Число граней (Г) |
Число вершин (В) |
Число рёбер (Р) |
Форма |
Число |
Сумма |
|
Тетраэдр |
|
||||||
|
Куб |
|
||||||
|
Октаэдр |
|
||||||
|
Икосаэдр |
|
||||||
|
Додекаэдр |
|
Обсуждение
и проверка заполненной таблицы.
III. Рефлексия:
1) Что нового я сегодня
узнал на уроке?
2) Чему научился
на уроке?
3) Что вызвало
трудности?
IV. Д/з: 1)
конспект урока; 2) изготовить модели правильных многогранников из любого
материала: картон, пластмасса, дерево, нитки или др. (развёртки даны в учебнике
Атанасян «Геометрия» , 10 — 11 класс); 3) написать мини — сочинение
«Геометрия вокруг нас».