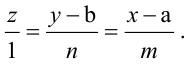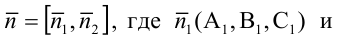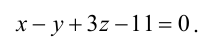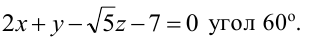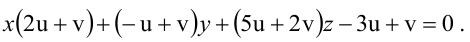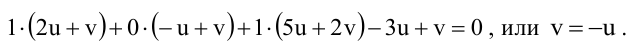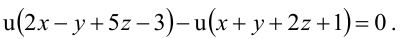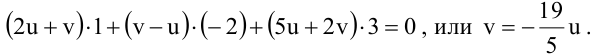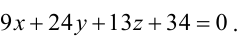Взаимное расположение прямой и плоскости в пространстве допускает три случая. Прямая и плоскость могут пересекаться в одной точке. Они могут быть параллельны. Наконец, прямая может лежать в плоскости. Выяснение конкретной ситуации для прямой и плоскости зависит от способа их описания.
Предположим, что плоскость π задана общим уравнением π: Ax + By + Cz + D = 0, а прямая
L — каноническими уравнениями (x — x0)/l = (y — y0)/m = (z — z0)/n. Уравнения прямой дают координаты точки M0(x0; у0; z0) на прямой и координаты направляющего вектора s = {l; m; n} этой прямой, а уравнение плоскости — координаты ее нормального вектора n = {A; B; C}.
Если прямая L и плоскость π пересекаются, то направляющий вектор s прямой не параллелен плоскости π. Значит, нормальный вектор n плоскости не ортогонален вектору s, т.е. их скалярное произведение не равно нулю. Через коэффициенты уравнений прямой и плоскости это условие записывается в виде неравенства A1 + Bm + Cn ≠ 0.
Если прямая и плоскость параллельны или прямая лежит в плоскости, то выполняется условие s ⊥ n, которое в координатах сводится к равенству Al + Bm + Cn = 0. Чтобы разделить случаи «параллельны» и «прямая принадлежит плоскости «, нужно проверить, принадлежит ли точка прямой данной плоскости.
Таким образом, все три случая взаимного расположения прямой и плоскости разделяются путем проверки соответствующих условий:
Если прямая L задана своими общими уравнениями:
то проанализировать взаимное расположение прямой и плоскости π можно следующим образом. Из общих уравнений прямой и общего уравнения плоскости составим систему трех линейных уравнений с тремя неизвестными
Если эта система не имеет решений, то прямая параллельна плоскости. Если она имеет единственное решение, то прямая и плоскость пересекаются в единственной точке. Последнее равносильно тому, что определитель системы (6.6)
отличен от нуля. Наконец, если система (6.6) имеет бесконечно много решений, то прямая принадлежит плоскости.
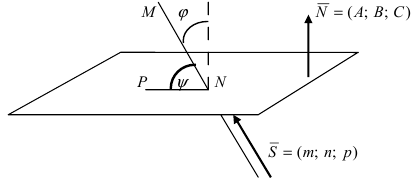
Угол между прямой и плоскостью. Угол φ между прямой L: (x — x0)/l = (y — y0)/m = (z — z0)/n и плоскостью π: Ax + By + Cz + D = 0 находится в пределах от 0° (в случае параллельности) до 90° (в случае перпендикулярности прямой и плоскости). Синус этого угла равен |cosψ|, где ψ — угол между направляющим вектором прямой s и нормальным вектором n плоскости (рис. 6.4). Вычислив косинус угла между двумя векторами через их координаты (см. (2.16)), получим
Условие перпендикулярности прямой и плоскости эквивалентно тому, что нормальный вектор плоскости и направляющий вектор прямой коллинеарны. Через координаты векторов это условие записывается в виде двойного равенства
A/l = B/m = C/n. (6.8)
3.1. Основные сведения из теории
Пусть прямая задана каноническими
уравнениями
:
,
а плоскость –
общим уравнением
:
.
1. Угол между прямой и плоскостью равен
углу между направляющим вектором
прямой и нормальным вектором
плоскости и вычисляется по формуле
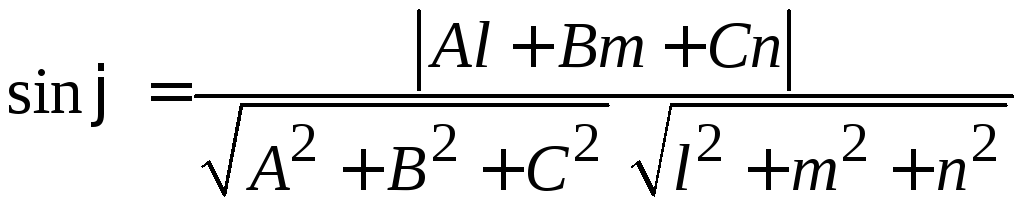
(3.1)
2. Условие параллельности прямой и
плоскости имеет вид
.
Оно равносильно условию ортогональности
векторов
и
3. Условие перпендикулярности прямой и
плоскости имеет вид
.
Оно равносильно условию коллинеарности
векторов
и
.
4. Условие принадлежности прямой
плоскости
записывается в виде
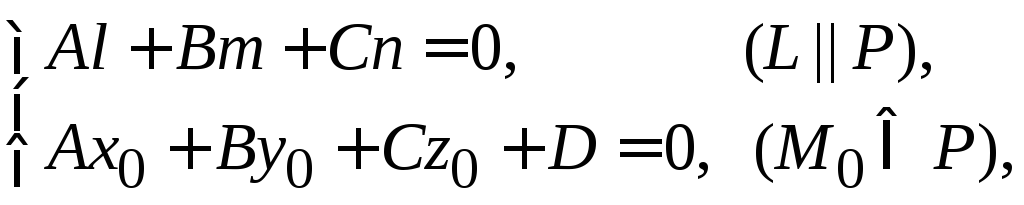
где
координаты точки
,
принадлежащей прямой.
3.2. Решение типовых задач
Задача 3.1. Найти острый угол между
прямойи плоскостью
.
Решение. Направляющий вектор прямой
равен.
Нормальный вектор плоскости равен.
По формуле (3.1)

.
Ответ:
Задача 3.2. При
каком значении
прямая
:

:
?
Решение. Согласно
условию задачи прямая
задана как линия пересечения двух
плоскостей. Нормальный вектор первой
плоскости равен,
нормальный вектор второй плоскости
равен.
Направляющий вектор прямой равен(см. формулу (2.6)):

Условие параллельности
прямой
и плоскости
это условие ортогональности направляющего
вектора прямойи нормального вектора плоскости
,
т. е..
Умножая, получаем
.
Таким образом, уравнение плоскости
будет
.
Ответ:
Задача 3.3. При каких значенияхи
прямая
лежит в плоскости
?
Решение. Прямая
будет параллельна плоскости, если ее
направляющий вектор
будет ортогонален нормальному вектору
плоскости,
т. е..
Запишем это условие:
Прямая будет принадлежать плоскости,
если координаты точки
,
через которую проходит прямая,
удовлетворяют уравнению плоскости:.
Отсюда получаем, что
При решении задачи мы воспользовались
формулой (3.2).
Ответ:
Задача 3.4. Найти точку пересечения
прямой:
и плоскости
:
Решение. Запишем уравнения прямой
в параметрическом виде
Подставляя выражения для
в уравнение плоскости
,
получим
Теперь следует подставить значение
параметра
в параметрические уравнения прямой
.
Находим.
Ответ:
Полезная
формула. Если прямаяпересекается с плоскостью
,
то точке пересечения
отвечает значение параметра
.
(3.3)
Задача 3.5. Найти уравнение плоскости,
проходящей через прямую:
перпендикулярно плоскости
:
Р
имеет два направляющих вектора
и
и проходит через точку
(рис. 3.1). Согласно формуле (1.9) ее уравнение
будет иметь вид

или
.
Окончательно:
.
Ответ:.
З
3.6.Известны
координаты вершин тетраэдра:
Найти уравнение и длину его высоты
.
Р
ешение.Данный тетраэдр мы
рассматривали в задаче 1.10. Уравнение
основанияимеет вид
.
В качестве направляющего векторавысоты
можно выбрать нормальный вектор грани
,
т. е.(рис. 3.2). Кроме того, нам известны
координаты точки,
через которую проходит высота.
Воспользуемся каноническими уравнениями
прямой (2.3). Тогда получим
:
.
Высоту
можно найти по формуле (1.5), определяющей
расстояние от точкидо грани
:
.

(Напомним, что
– это коэффициенты в общем уравнении
плоскости,
и они равны,
,
,
.)
Ответ: :
;

Задача 3.7. Даны прямые:
и
:
.
Найти уравнение плоскостипроходящей через прямую
параллельно прямой
Решение. Векторы
и
являются направляющими векторами
плоскости(рис. 3.3). Точка
принадлежит плоскости
.
Решаем задачу, используя формулу (1.9):

или
.
Окончательно:
.
Ответ: .
Задача 3.8. Составить уравнение
плоскости, проходящей через прямую:
и точку
.
Решение.Прямаяпроходит через точку
и ее направляющий вектор равен
.
Произвольная точкабудет принадлежать искомой плоскости
,
если векторы
и
компланарны:
(рис. 3.4), т. е.

Это и есть уравнение плоскости
.
Подставляем координаты:
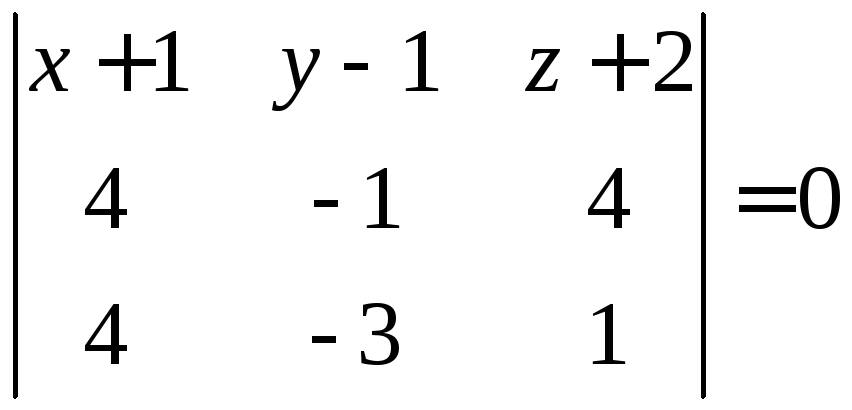
или
.
Окончательно:
.
Ответ: .
Полезная
формула. Уравнение
плоскости, проходящей через прямую
:
и точку
,
не лежащую на этой прямой, имеет вид

Задача 3.9. Доказать,
что прямые
:
:
лежат в одной плоскости и найти уравнение
этой плоскости.
Р
Первая прямая проходит через точку
и ее направляющий вектор
.
Вторая прямая проходит через точкуи ее направляющим вектором является
.
Очевидно, что прямые лежат в одной
плоскости, если векторы,
и
компланарны:
(рис. 3.5), т. е.

Подставим заданные координаты:

Это означает, что прямые
и
лежат в одной плоскости. Векторы
и
не коллинеарны. Следовательно, эти
прямые пересекаются.
Найдем уравнение
плоскости
,
в которой лежат прямыеи
.
Очевидн
что произвольная точкабудет принадлежать плоскости, если
векторы,
,
компланарны:
(рис. 3.6), т. е.

Это и есть уравнение искомой плоскости.
Подставляем координаты и вычисляем
определитель разложением по элементам
первой строки. Получаем
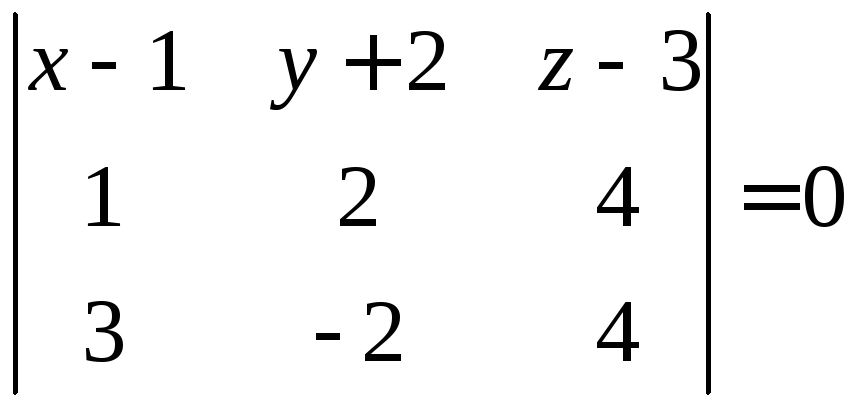
или
.
Окончательно:
.
Ответ: .
Полезные
формулы. Две прямые
:
:
лежат в одной плоскости, если
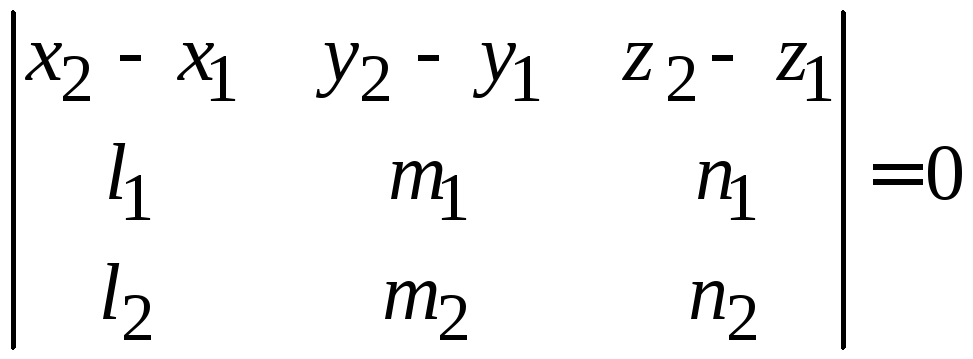
(3.5)
Если прямые пересекаются, то уравнением
этой плоскости будет

(3.6)
Замечание.
Прямые скрещиваются (т. е. не лежат в
одной плоскости) тогда и только тогда,
когда
и равенство (3.5) несправедливо.
Задача
3.10.Найти уравнение плоскости,
проходящей через две параллельные
прямые:
:
:
.
Р
ешение.Ясно, что направляющие
векторы этих прямых равны.
Первая прямая проходит через точку,
вторая
через точку.
Произвольная точкапринадлежит искомой плоскости
,
если векторы,
и
компланарны:
(рис. 3.7), т. е.
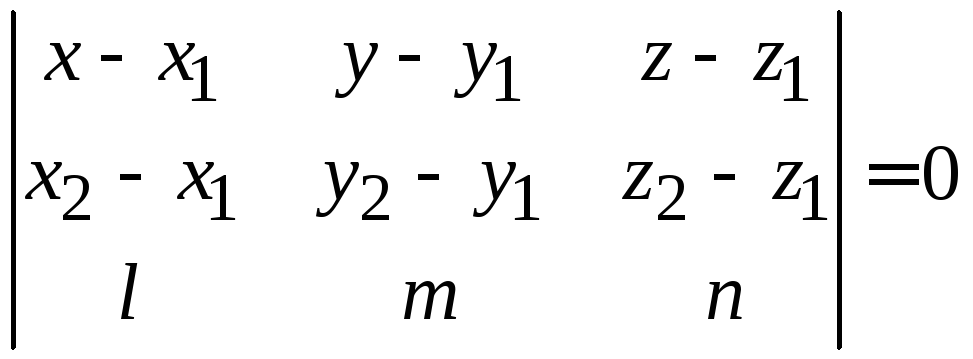
Подставляя заданные координаты, находим
уравнение плоскости

или
.
Окончательно:
.
Ответ: .
Полезная
формула. Уравнение плоскости, проходящей
через две параллельные прямые (,
)
:
:
,
имеет вид

(3.7)
Замечание. В задачах 1.3, 1.9, 3.5, 3.8–3.10
без труда можно указать два направляющих
вектора искомых плоскостей. Поэтому
решение этих задач аналогично решению
задачи 1.2. Если эти направляющие векторы
явно не обозначены в ходе решения, то
найдите их самостоятельно. Подумайте,
что общего в формулах (1.7)–(1.9), (3.4)–(3.7).
З
3.11.Найти координаты проекцииточки
на плоскость
:
.
Решение.Находим параметрические
уравнения прямой,
проходящей через точкуперпендикулярно плоскости
.
В качестве направляющего векторапрямой
можно выбрать нормальный вектор
плоскости
,
т. е. положить(рис. 3.8). Параметрические уравнения
прямойбудут (см. формулу (2.2)):
По формуле (3.3) находим значение параметра
,
при котором прямая пересекает плоскость.
Получим.
Подставим это значение в параметрические
уравнения прямой и вычислим координаты
точки
Ответ:
Задача 3.12.
Найти координаты
точки
,
симметричной точкеотносительно плоскости
:
.
Р
результатом решения предыдущей задачи.
Точка
– проекция
точки
на плоскость. Координаты точки
можно найти, используя соотношения:
(рис. 3.9). Следовательно,
Ответ:
Задача 3.13. Найти
координаты проекции
точки
на прямую
:
.
Р
Найдем уравнение плоскости
,
перпендикулярной прямойи проходящей через точку
.
В качестве нормального вектораплоскости
можно выбрать направляющий вектор
прямой
,
т. е. положить(рис. 3.10). Тогда уравнение плоскости
:
или
Параметрические уравнения прямой
имеют вид
Далее решаем аналогично задаче 3.11.
Координаты точки
находим с помощью формулы (3.3). Получаем
,
Ответ:
З
3.14.Найти координаты точки,
симметричной точкеотносительно прямой
:
Решение.
Воспользуемся результатом задачи 3.13.
Точка
проекция точки
на прямую
.
Координаты точки
можно найти, используя соотношения:
(рис. 3.11). Следовательно,
Ответ:
Задача 3.15. Найти расстояние между
параллельными прямыми
.
Р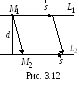
длину перпендикуляра ,
опущенного из точки
,
через которую проходит прямая,
на прямую.
Для этого построим параллелограмм со
сторонамии
(рис. 3.12). Здесь
– точка, через которую проходит прямая
,
анаправляющий вектор прямых (так как
прямые параллельны, то).
Площадьпараллелограмма вычисляется с помощью
векторного произведения векторови
:
.
Расстояние
получим, разделив площадь параллелограмма
на длину его стороны
:
Ответ:
Полезная
формула. Если заданы две параллельные
прямые
;
,
то расстояние
между
ними вычисляется по формуле

где
и
точки, через которые проходят прямые
и
соответственно,
их направляющий вектор.
Задача 3.16. Найти расстояние между
скрещивающимися прямыми:
Р
Прямая
проходит через точку
и ее направляющий вектор
.
Прямаяпроходит через точку
и ее направляющий вектор
.
Известно, что если прямые скрещиваются,
то существуют две параллельные плоскостии
такие, что прямая
лежит в плоскости
,
а прямая
в плоскости
.
Направляющие векторыи
будут направляющими векторами этих
плоскостей.
Построим параллелепипед,
сторонами которого являются векторы
(рис. 3.13). Найдем его объем. Для этого
вычислим смешанное произведение
Таким образом, объем
Теперь найдем площадь основания
параллелепипеда (см. решение задачи
3.15):

Расстояние
между
скрещивающимися прямыми будет равно
Ответ:
Полезная
формула. Если заданы две скрещивающиеся
прямые

то расстояние между ними вычисляется
по формуле
Здесь
и
– точки, через
которые проходят прямые
и
соответственно,
и
– их направляющие
векторы.
Замечание. Кратко опишем другой
способ решения задачи 3.16. Сначаланайдем
уравнение плоскости
(проделайте это самостоятельно). Оно
будет
.
Расстояние
равно расстоянию от точки
до плоскости
.
Теперь все следует из формулы (1.5):
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.6.1. Взаимное расположение прямой и плоскости
Рассмотрим плоскость и прямую
, заданную точкой
и направляющим вектором
.
Существует три варианта взаимного расположения прямой и плоскости:
1) прямая пересекает плоскость в некоторой точке ;
2) прямая параллельна плоскости: ;
3) прямая лежит в плоскости: . Да, так вот нагло взяла, и лежит.
Как выяснить взаимное расположение прямой и плоскости?
Это заметно проще, чем выяснить взаимное расположение двух прямых.Изучим аналитические условия, которые позволят нам ответить на данный вопрос.
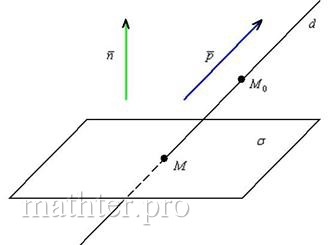
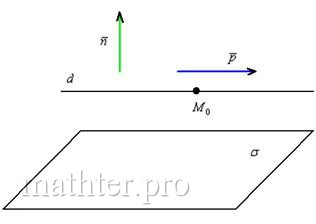
Выполним схематический чертёж, на котором прямая пересекает плоскость:
1) Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор
не ортогонален нормальному вектору плоскости. Из этого следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля:
.
В координатах это условие запишется следующим образом:
Если же данные векторы ортогональны, то их скалярное произведение равно нулю: , и прямая либо параллельна плоскости, либо лежит в ней.
Разграничим эти случаи:
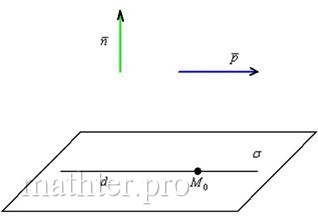
2) Если прямая параллельна плоскости (рисунок внизу слева), то любая точка прямой не удовлетворяет уравнению плоскости:
. Таким образом, условие параллельности прямой и плоскости записывается системой:
3) Если прямая лежит в плоскости (рис. справа) то любая точка прямой удовлетворяет уравнению плоскости:
, и аналитические условия данного случая запишутся системой:
Алгоритм выяснения взаимного расположения прямой и плоскости достаточно примитивен – всего в два шага. Кроме того, оформляя задачи, можно обойтись вообще без составления системы:
Задача 160
Выяснить взаимное расположение прямой, заданной точкой и направляющим вектором
, и плоскости
.
Решение: вытащим нормальный вектор плоскости: .
Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: , значит, данные векторы ортогональны и прямая либо параллельна плоскости, либо лежит в ней.
Подставим координаты точки в уравнение плоскости:
Получено верное равенство, следовательно, точка лежит в данной плоскости, и вообще все точки прямой лежат в ней.
Ответ: прямая лежит в плоскости
Самостоятельно:
Задача 161
Выяснить взаимное расположение плоскости и прямой
.
Решение и ответ в конце книги.
И после небольшой разминки начинаем накидывать «блины» на штангу:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 — плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
4. 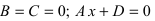
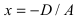
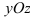
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 — уравнение описывает плоскость 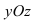
Рис. 40. Координатная плоскость 
Другие уравнения плоскости
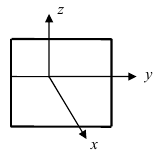
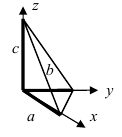
1. Уравнение плоскости в отрезках. Пусть в уравнении 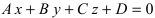
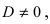
Введем следующие обозначения 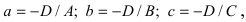
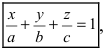
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
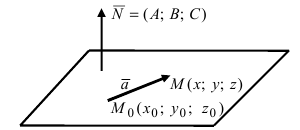
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 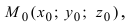
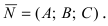
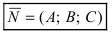
Возьмем на плоскости произвольную точку 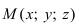
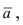
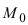
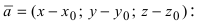
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 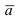
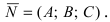
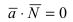
Пример:
Составить уравнение плоскости, проходящей через т. 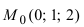
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 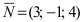
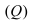
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 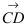
Решение:
Построим на искомой плоскости вектор 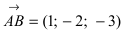
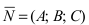
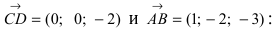
Уравнение плоскости, проходящей через заданную точку 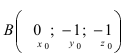
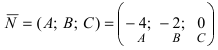
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 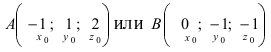
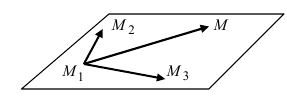
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 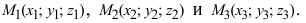
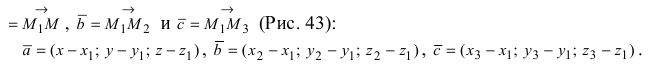
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 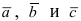
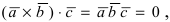
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 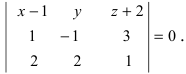
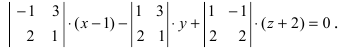
Основные задачи о плоскости в пространстве
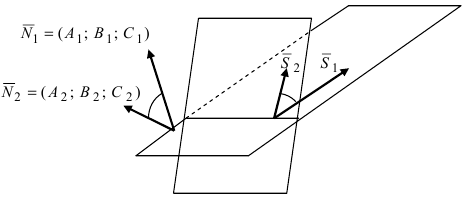
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 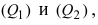
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 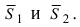
Рис.44. Угол между плоскостями.
В силу того, что 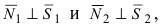
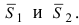
Следствие: Если плоскости перпендикулярны (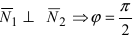
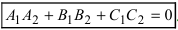
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 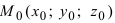
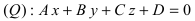
Пример:
На каком расстоянии от плоскости 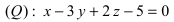
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 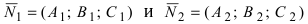
Пусть прямая проходит через точку 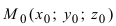
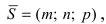
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 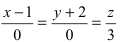
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 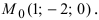
Пример:
Записать уравнение прямой 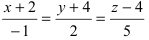
Решение:
Приравняем каждую дробь к параметру t: 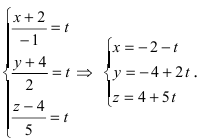
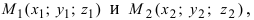
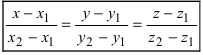
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
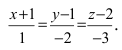
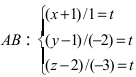
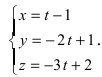
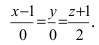
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением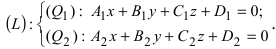
Пример:
Записать уравнение прямой 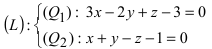
Решение:
Положив х = 0, получим СЛАУ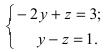
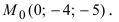
Запишем каноническое 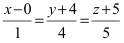
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 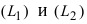
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (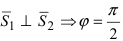
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 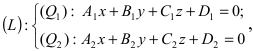
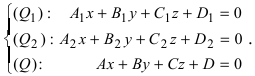
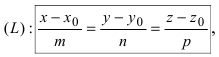
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 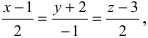
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 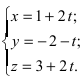
Найденное значение параметра 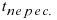
- Заказать решение задач по высшей математике
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 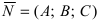
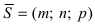
Рис. 45. Угол между прямой и плоскостью.
Угол 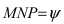
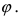
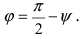
Следствие: Если прямая перпендикулярна плоскости (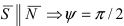
Следствие: Если прямая параллельна плоскости (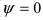
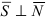
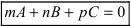
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 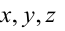

Вектор 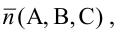
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 — плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 — плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 — плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 — плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 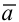
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 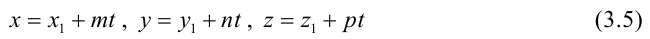
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 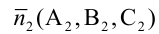
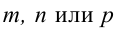
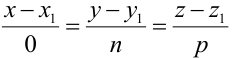
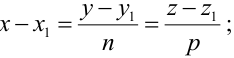
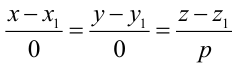
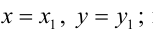
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 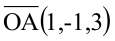
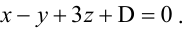
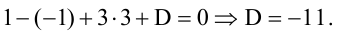
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением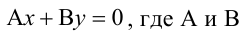
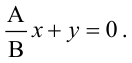
Решая квадратное уравнение 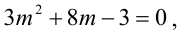
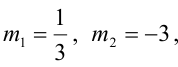
Пример:
Составьте канонические уравнения прямой: 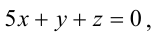
Решение:
Канонические уравнения прямой имеют вид:
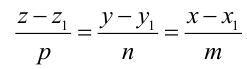
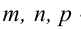
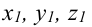
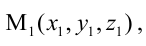
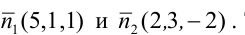
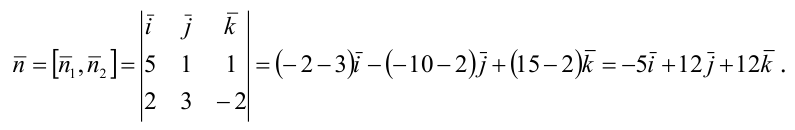
Пример:
В пучке, определяемом плоскостями 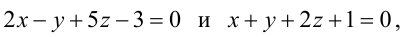
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 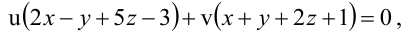
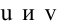
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 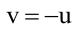
Т.к. и 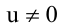
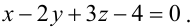
Значит, уравнение второй плоскости имеет вид: 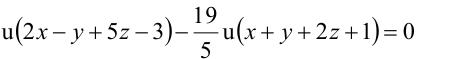
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
Взаимное расположение прямой и плоскости в пространстве
Содержание:
-
Понятие плоскости и ее обозначения
- Понятие плоскости
- Обозначение плоскости
-
Как выяснить взаимное расположение прямой и плоскости
- Прямая пересекает плоскость
- Прямая принадлежит плоскости
- Прямая параллельна плоскости
- Различные способы задания прямой на плоскости
- Как найти угол между прямой и плоскостью
Понятие плоскости и ее обозначения
Понятие плоскости
Плоскости окружают нас со всех сторон. Примеры плоских поверхностей: стол, стены, пол и потолок, школьная доска, скамейка, экран, грани карандаша. Плоскость — одно из важнейших понятий геометрии и стереометрии, математики давно пытаются дать ее точное определение.
Евклид (III век до н. э.): «Поверхность есть то, что имеет только длину и ширину», «плоская поверхность есть та, которая одинаково расположена относительно прямых линий, на ней лежащих».
Фурье (1768-1830): «Плоскость есть геометрическое место всех прямых, перпендикулярных к данной прямой в данной на ней точке».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Лежандр (1752-1833): «Плоскость — это поверхность, с которой прямая, имея с ней две общие точки, совмещается всеми своими точками, где бы на плоскости ни были взяты эти точки».
Плоскость — это такая поверхность, в которой целиком лежит всякая прямая, соединяющая две любые точки этой поверхности.
Обозначение плоскости
Невозможно изобразить объект, бесконечно простирающийся в длину и ширину. Поэтому для плоскости приняты условные обозначения. На рисунке вместо плоскости изображают ее часть: параллелограмм или «облако» — овал, область с неровными краями.
Плоскость обозначают строчными буквами греческого алфавита: α (альфа), β (бета), γ (гамма) и т.д.
Как выяснить взаимное расположение прямой и плоскости
Есть три варианта взаимного расположения прямой и плоскости в пространстве:
- Прямая и плоскость пересекаются.
- Прямая принадлежит плоскости (лежит в ней).
- Прямая и плоскость параллельны.
Рассмотрим каждый вариант подробней.
Прямая пересекает плоскость
Прямая и плоскость пересекаются, если они имеют только одну общую точку.
Прямая принадлежит плоскости
Прямая принадлежит плоскости (лежит в плоскости), если все точки прямой лежат в плоскости. При этом достаточно, чтобы две любые точки данной прямой лежали в данной плоскости.
Аксиома 1
Все точки прямой лежат в плоскости, если хотя бы две точки данной прямой лежат в данной плоскости.
Прямая параллельна плоскости
Прямая, не лежащая в плоскости, пересекается с плоскостью или параллельна ей. Прямая и плоскость параллельны, если они не имеют общих точек. Отсутствие общих точек — признак параллельности прямой и плоскости.
Теорема 1
Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости.
Различные способы задания прямой на плоскости
Положение прямой определяют:
- Две заданные точки. Через две точки можно провести только одну прямую. Поэтому координаты точек в прямоугольной системе координат задают отрезок или прямую.
- Точка, через которую она проходит, и параллельная прямая.
- Точка и направляющий вектор.
- Точка и перпендикулярная прямая.
Как найти угол между прямой и плоскостью
Чтобы найти угол между прямой и плоскостью, нужно знать, каков угол между прямой и ее проекцией на эту плоскость.
На изображении прямая АВ пересекает плоскость γ, и является наклонной к этой плоскости. Проведем перпендикуляр АС. ВС — проекция наклонной АВ. Угол между АВ и γ будет равен ∠АВС прямоугольного ΔАСВ.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так

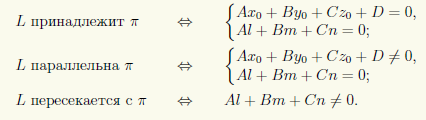
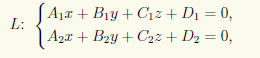
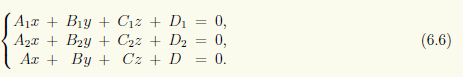
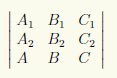
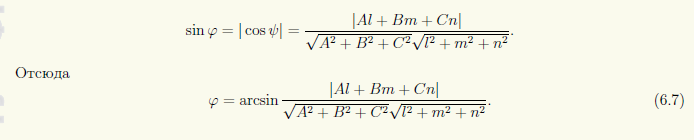






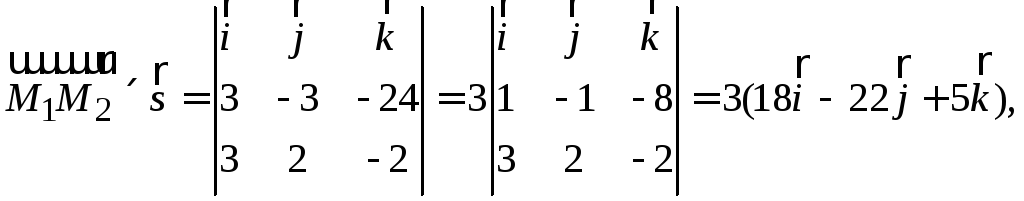






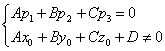
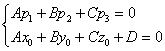
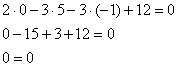
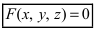
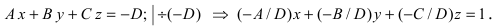
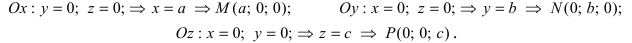
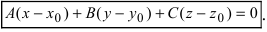
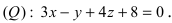
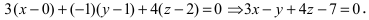
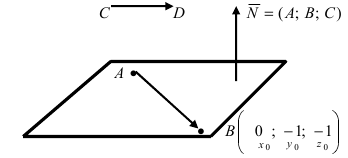
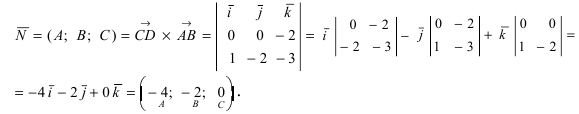
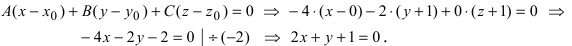

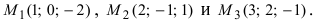
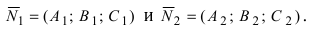
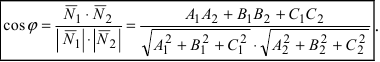
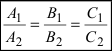
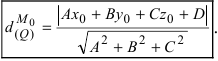
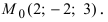
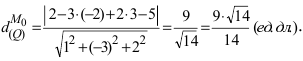
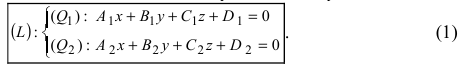
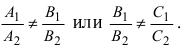

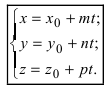
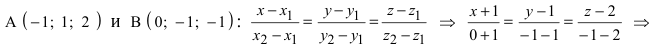
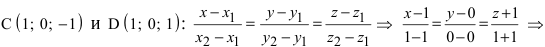
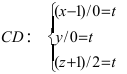
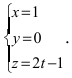
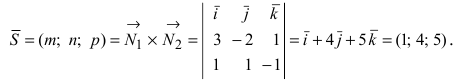
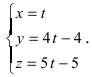
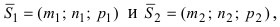

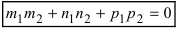
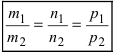
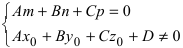 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);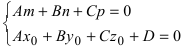 прямая лежит на плоскости;
прямая лежит на плоскости;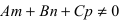 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.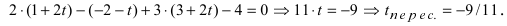
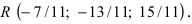
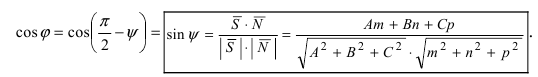
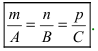
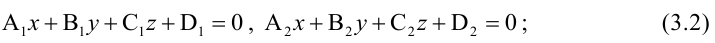
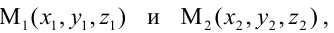 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: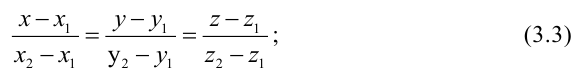
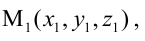 ей принадлежащей, и вектором
ей принадлежащей, и вектором 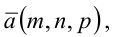 ей коллинеарным.
ей коллинеарным.