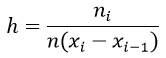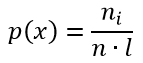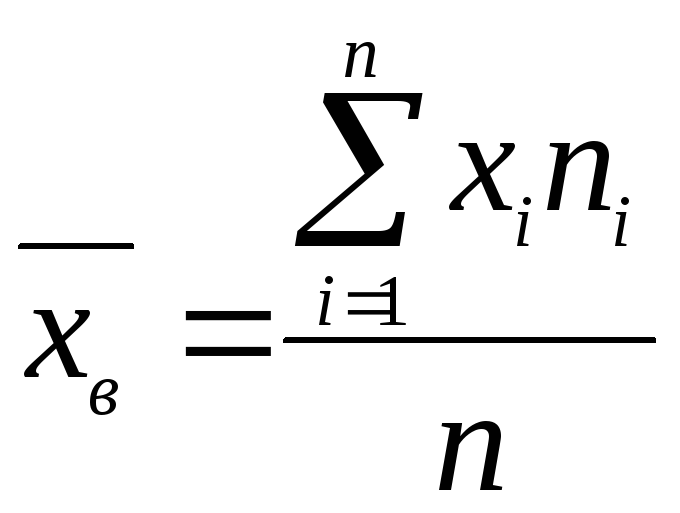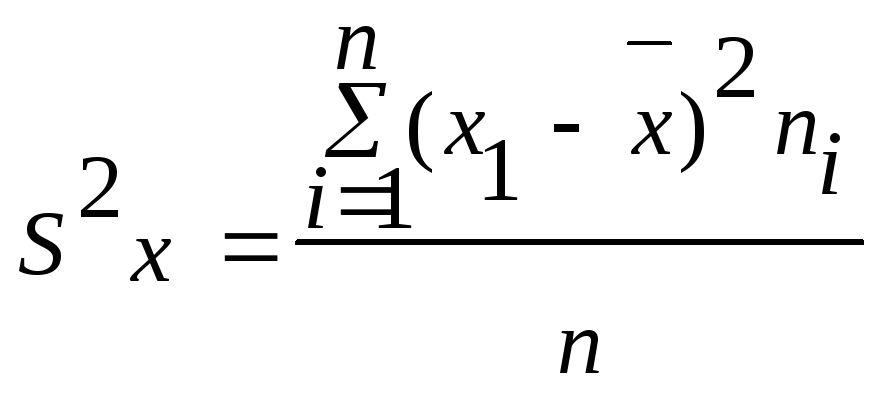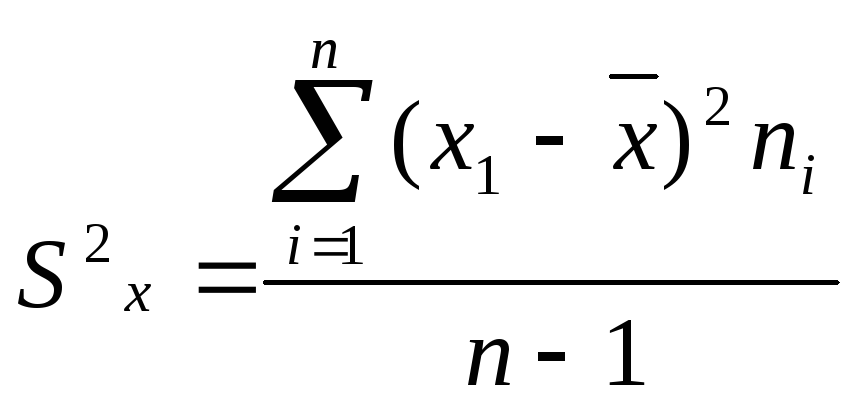Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:
xi-xi-1
Высоты гистограммы определяется по формуле:
Формула размаха выборки R:
R=xmax−xmin
Количество интервалов в выборке определяется по формуле:
k≈1+log2n≈1+3,221·lgn
Длина l интервала гистограммы, формула:
l=R/n
Формула эмпирической плотности распределения выборки имеет вид:
хi — значения частот;
ni — частоты;
wi — относительные частоты;
n — объём выборки;
В водоёме проведены измерения температуры воды в течение 20 дней.
Статистика отчета измерений:
11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16
Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.
Решение.
По условию задачи объем выборки равен 20.
Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:
11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21
Найдем размах выборки
R=21-11=10
Количество интервалов в выборке равно:
k≈log220+1≈5,32
Округляя до целого числа, имеем
k=5
Определим длину каждого интервала
l=10/5=2
Получаем таблицу интервалов
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
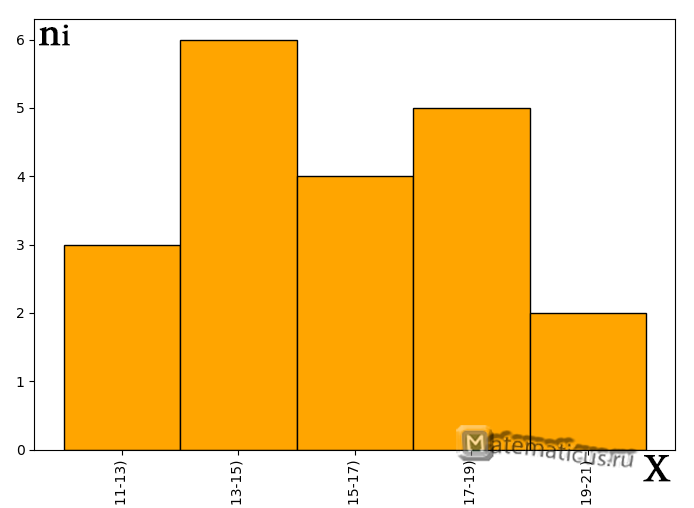
| 1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
Таблица относительных частот и эмпирическая плотность распределения частоты
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
График гистограммы относительных частот
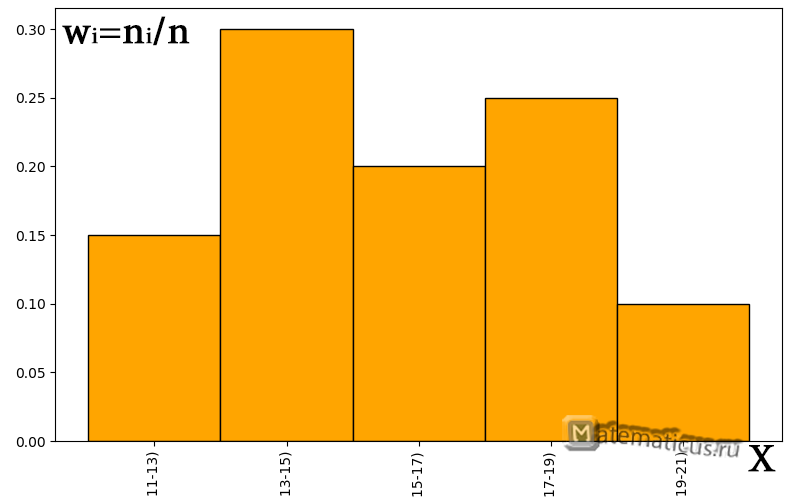
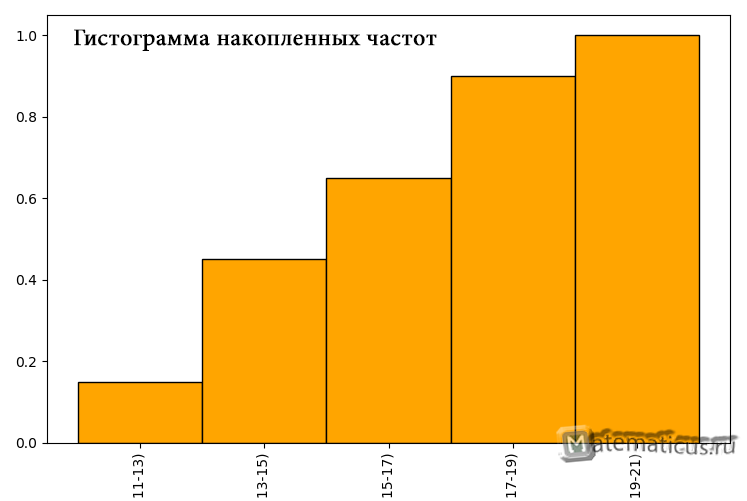
График гистограммы накопленных частот
Полигон в статистике — это график (или ломанная линия), отрезки которой соединяют точки с координатами хi, wi в прямоугольной системе координат между собой (см. рисунок ниже) и наглядно показывает распределение частот как для количественных, так и порядковых значений переменных, то плотность распределения случайной величины.
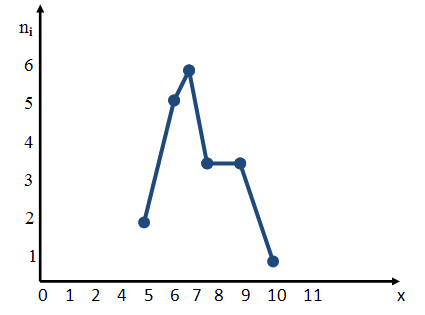
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Пример графика полигона частот хi, ni
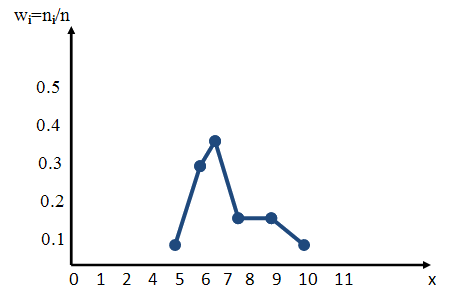
Пример графика полигона относительных частот хi, wi
22811
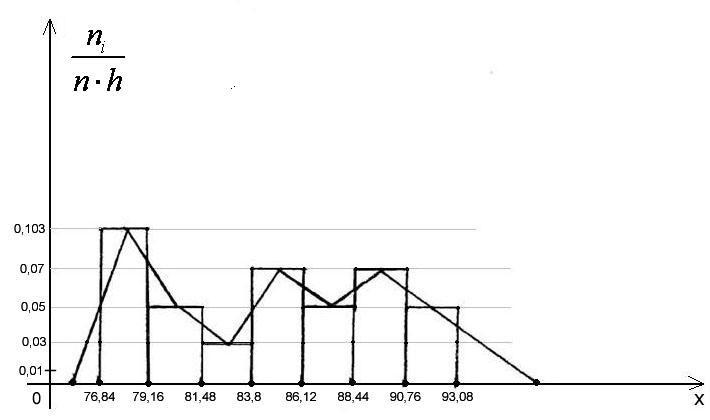
Гистограмма и полигон плотности относительных частот
f*=-плотность
относительных частот.
—
длина соответствующего интервала
К=1+3,32ּlg(n)
— количество классов (интервалов)
Плотность
относительных частот f*
показывает,
какая доля объектов совокупности
приходится на единицу интервала.
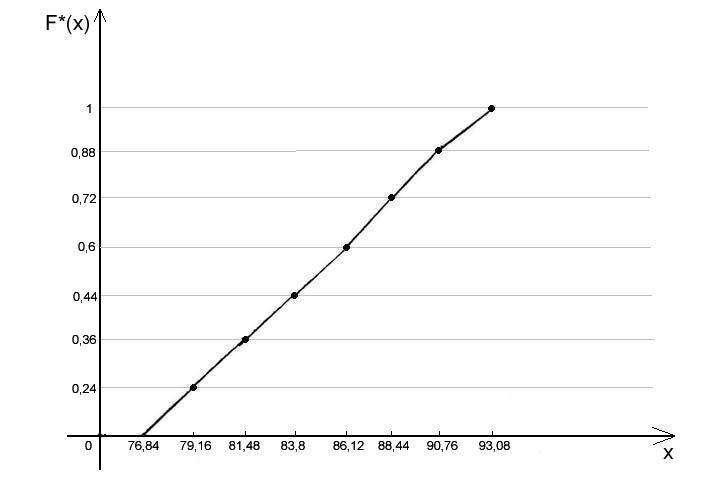
Геометрическое
представление эмпирической функции
распределения F*(x)
называется кумулятой
или кумулятивной
кривой.
,
где
—
накопленная абсолютная частота признака.
1.3. Числовые характеристики вариационного ряда
Для
того, чтобы количественно охарактеризовать
самые существенные свойства распределения,
а также для того, чтобы можно было
сравнить разные распределения, вычисляют
средние показатели — выборочные
числовые характеристики.
В
статистике используются различные
величины в зависимости от того, какие
цели при анализе материала ставит
исследователь. Понятием средней величины
пользуемся в тех случаях, когда требуется
определить средний надой по стаду,
средний привес, средний прирост стада,
средние клинические показатели
деятельности сердца, лёгких, среднего
состава крови и во многих других случаях.
Различают
следующие виды средних величин: средняя
арифметическая, средняя геометрическая,
средняя квадратическая, средняя
гармоническая, мода и медиана.
Наиболее
распространенным видом средних величин
является средняя арифметическая, которая
бывает простой и взвешенной.
Возможны
следующие случаи:
1.
Результаты наблюдения не сведены в
вариационный ряд или все частоты равны
единице или одинаковы. Тогда вычисляют
простую среднюю арифметическую
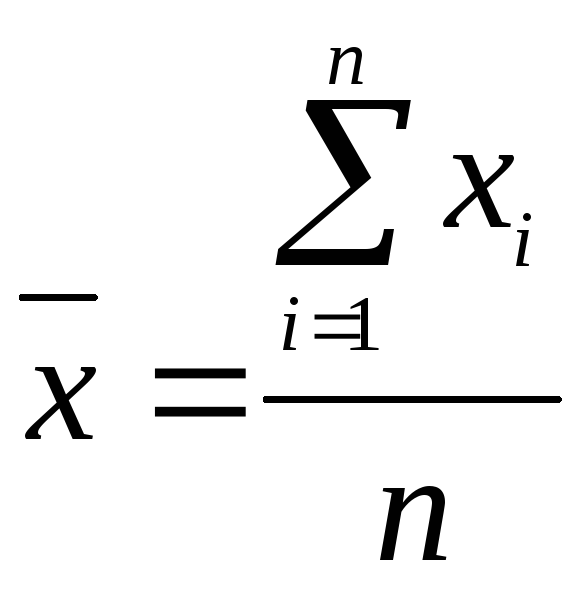
где
хi
– значение признака
n
– объём результатов (число наблюдений).
2.
Частоты ni
отличны друг от друга, то есть значения
признака хi
повторяются. В этом случае вычисляют
среднюю арифметическую взвешенную
(выборочную среднею)
3.
Распределение интервальное. В этом
случае вместо хi
берут середину интервалов
Математические
ожиданием
(или средним значением) дискретной
случайной величины Х, имеющий закон
распределения, называется число, равное
сумме произведений всех её значений на
соответствующие им вероятности.
Обозначаются
М(Х)
Дисперсия
характеризует рассеяние значений
признака относительно выборочной
средней
.
Выборочная
дисперсия
–
это среднее арифметическое значение
квадратов отклонения признака от
выборочной средней.
Для
её вычисления применяют формулу
В
случае, если общее число вариант мало
(n<30),
лучше применять формулу
Выборочное
среднее квадратичное отклонение
Sx
находят по формуле
,
а
исправленное выборочное среднее
квадратичное отклонение S
по формуле
Коэффициент
вариации V
– это выборочное процентное отношение
выборочного среднего квадратичного
отклонения к выборочной средней
Коэффициент
вариации показывает изменчивость
признака.
Если
Сv
>
20% -изменчивость значительная; если 10%
< Cv
<
20%- средняя; если Cv
<
10%- незначительная.
Коэффициент
вариации позволяет сравнивать изменчивость
признаков, имеющих разные единицы
измерения.
В
качестве описательных характеристик
вариационного ряда используется медиана,
мода, размах вариации (выборки) и т.д.
Размахом
вариации
называется число
R=Xmax
—
Xmin,
где
Хmax-наибольший,
Xmin-наименьший
вариант ряда.
Медиана
– это значение варианта, который делит
ранжированный ряд на равные по числу
вариант части.
4
7 12 8 9 5 7 13 15
Ме
= 12 Ме
=
Если
признак Хпредставлен интервально:
медианному
интервалу соответствует первая
накопленная частота превосходящая
n/2.
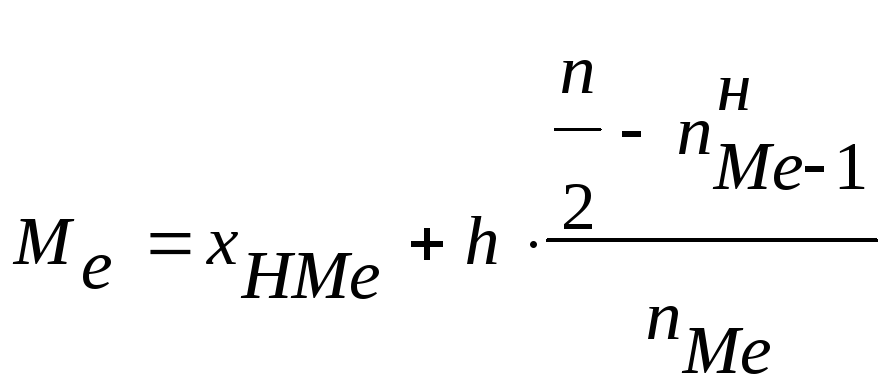
где
—
нижняя граница медианного интервала
–шаг
разбиения, ширина класса
–накопленная
частота интервала, предшествующего
медианному интервалу
—
абсолютная частота медианного интервала.
Модой
называется вариант, имеющий наибольшую
частоту.
Класс
с наибольшей частотой называется
модальным.
Для
определения моды интервальных рядов
служит формула
,
где
— нижняя граница модального интервала
–ширина
класса
–абсолютная
частота модального интервала
–абсолютная
частота интервала предшествующего
модальному
–абсолютная
частота интервала следующего за
модальным.
При
изучении распределений, отличных от
нормального, возникает необходимость
количественно оценить это различие.
Вводят специальные характеристики:
асимметрию и эксцесс.
Для
нормального распределения эти
характеристики равны нулю.
Асимметрией
теоретического распределения
называют
отношение центрального
момента
третьего порядка к кубу среднего квадрата
отклонения.
Центральным
моментом порядка k
случайной
величины X
называется математическим ожиданием
величины (X
– M(X))k,
обозначается через μk.
Таким
образом, по определению
μk
= M(X
– M(X))k.
В
частности, μ2
= D(X),
то есть центральный момент 2-го порядка
есть дисперсия
μ1
= M(X
– M(X))
= 0
Для
дискретной случайной величины
Среди
моментов высших порядков особое значение
имеют центральные моменты 3-го и 4-го
порядков, называемых соответственно
коэффициентами асимметрии и эксцесса.
Коэффициентом
асимметрии («скошенности») А
случайной
величины X
называется величина
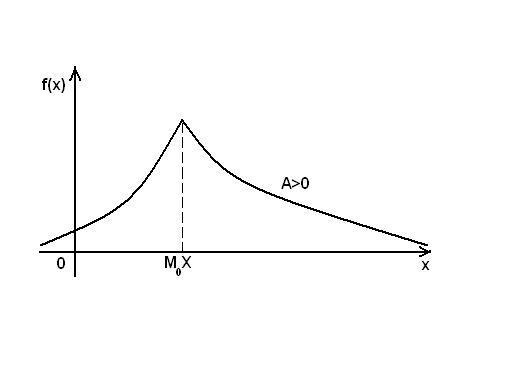
Если
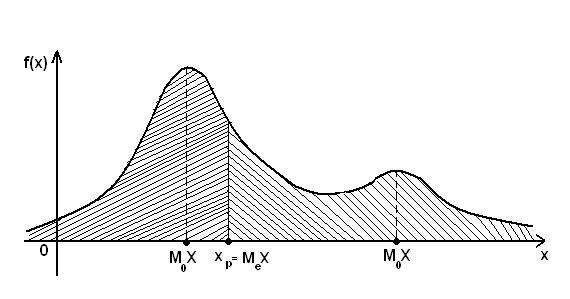
А > 0, то кривая распределения более
полога справа от М0(X);
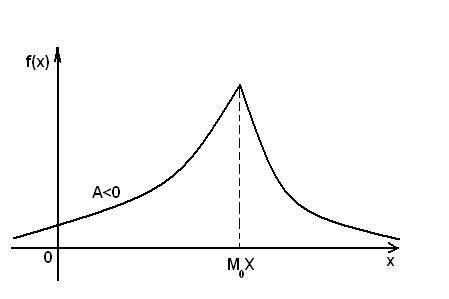
если
А < 0, то кривая распределения более
полога слева от М0(X).
Коэффициентом
эксцесса («островершинности»)
Е
случайной величины X
называется величина
Величина
Е характеризует островершинность или
плосковершинность распределения.
Для
нормального закона распределения А = 0
и Е = 0; остальные распределения сравниваются
с нормальным: если
Е
> 0 – более островершинные, а распределения
«плосковершинные» имеют Е < 0
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Полигон и гистограмма
ni — частоты;
wi — относительные частоты;
n — объём выборки;
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
| 1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
Таблица относительных частот и эмпирическая плотность распределения частоты
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/ Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
График гистограммы относительных частот
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Источник
Как найти плотность относительных частот
В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.
Пусть требуется измерить некоторую величину . Результаты измерений
естественно рассматривать как значения случайных величин , полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить . Следовательно, возникает задача оценить параметр . Для решения задачи рассмотрим случайную величину
Это обстоятельство приводит к мысли построить статистические характеристики:
Первая представляет среднее арифметическое наблюденных значений случайной величины и статистическую дисперсию — во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины и к дисперсии
При ограниченности наблюдений эксперимента заменой и на и совершаем погрешность, а при небольшом числе наблюдений величины , являются случайными величинами. Возникает задача об оценке неизвестных параметров , случайной величины на основе экспериментальных данных, т.е. задача — найти подходящие значения этих параметров.
Множество результатов измерений величины называется выборкой объема . Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину рассматривать как случайную величину, функцию распределения которой
Полученный статистический материал , , . наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д.
Если выборка объема содержит различных элементов , причем встречается раз, то число называется частотой элемента , а отношение называется относительной частотой элемента . Очевидно, что
Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы ‘, а вторая — их частоты (относительные частоты .
Полигоном частот (относительных частот) выборки называется ломаная с вершинами в точках ( , ( ( , ).
Функция , где — объем выборки, а — число значений в выборке, меньших , называется эмпирической функцией распределения. Функция служит оценкой неизвестной функции распределения , т.е. .
Пусть теперь — непрерывная случайная величина с неизвестной плотностью вероятности . Для оценки по выборке разобьем область значений на интервалы длины . Обозначим через середины интервалов, а через число элементов выборки, попавших в указанный интервал. Тогда — оценка плотности вероятности в точке . В прямоугольной системе координат построим прямоугольники с основаниями и высотами , т.е. площади прямоугольника, равной относительной частоте данного разряда. Полученная таким образом фигура называется гистограммой выборки.
Пример 156. Имеются данные о количестве студентов в 30 группах физико-математического факультета:
| 26 | 25 | 25 | 26 | 25 | 23 |
| 23 | 24 | 19 | 23 | 20 | 19 |
| 22 | 24 | 24 | 23 | 20 | 23 |
| 24 | 19 | 21 | 18 | 21 | 18 |
| 20 | 18 | 18 | 21 | 15 | 15 |
Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.
Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:
| 15 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 2 | 4 | 2 | 4 | 3 | 1 | 5 | 4 | 3 | 2 |
Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками.
Пример 157. Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
| Кол-во баллов | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кол-во школьников | 2 | 3 | 2 | 4 | 12 | 10 | 8 | 9 |
Составить статистическое распределение количества школьников по количеству набранных баллов и построить полигон относительных частот.
Решение. Пусть = <количество набранных баллов>, a = <относительные частоты>. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
| X | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0,04 | 0,06 | 0,04 | 0,08 | 0,24 | 0,2 | 0,16 | 0,18 |
Чтобы построить полигон относительных частот, отложим на оси абсцисс значения , а на оси ординат — относительные частоты . После этого последовательно соединим полученные точки отрезками.
Пример 158. В 2002 году количество служб, представляющих гражданам жилищные субсидии, по сельским районам области распределено следующим образом:
Построить эмпирическую функцию распределения.
Решение. Найдем сначала статистический ряд распределения числа служб в районах области.
Эмпирическую функцию распределения находим аналогично интегральной функции (см. §13 ) [перейти].
Пример 159. Построить гистограмму следующей выборки объема 50
1 3 — 7 5 2 7 — 12 10 3 12 — 17 20 4 17 — 21 8 5 21 — 28 7
Решение. Найдем плотность относительной частоты для каждого интервала и заполним последний столбец таблицы:
Построим на оси абсцисс заданные интервалы и проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся на расстояниях, равных соответствующим плотностям относительной частоты .
Из способа построения гистограммы следует, что полная ее площадь равна единице.
Пример 160. Число школ Ярославской области в 2002 — 2003 учебном году по малым городам и районам составило:
Построить гистограмму распределения числа школ по районам области.
Решение. Выберем границы интервалов и составим по данной выборке следующую таблицу
1 13 — 17 6 2 17 — 20 3 3 20 — 25 4 4 25 — 31 4
Аналогично предыдущему примеру строим гистограмму числа школ, распределенных по малым городам и районам области.
«Сглаживая» полученную гистограмму, получаем «похожесть» данного дискретного закона распределения на классический показательный (непрерывный) закон. В этом и заключается основное предназначение гистограмм выборок.
На каких методах основано изучение статистических данных?
Основные задачи математической статистики.
Какие способы отбора из генеральной совокупности вы знаете?
Какая выборка называется представительной?
В чем отличие вариационного от статистического ряда?
Для чего используется полигон частот?
Свойства эмпирической функции распределения.
В каком случае и для чего строятся гистограммы?
I. 311. Записать выборку 2, 7, 3, 5, 4, 10, 5, 5, 2, 8, 10, 2, 7, 7, 7, 5, 4, 2, 4, 7, 8 в виде: а) вариационного ряда; б) статистического ряда.
312. Найдите эмпирическую функцию распределения для выборки, представленной вариационным рядом:
313. Имеются данные о количестве сельских населенных пунктов районов Ярославской области с численностью населения более 500 человек:
Большесельский — 4, Борисоглебский — 2, Брейтовский — 1, Гаврилов-Ямский — 2, Даниловский — 2, Любимский — 1, Мышкинский — 0, Некоузский — 6, Некрасовский — 5, Первомайский — 2, Переславский — 11, Пошехонский — 0, Ростовский — 11, Рыбинский — 12, Тутаевский — 3, Угличский — 4, Ярославский — 27.
Найдите вариационный ряд количества населенных пунктов Ярославской области с численностью населения более 500 человек. Постройте полигон частот.
314. В 2002 году количество крупных и средних промышленных предприятий по районам ( в том же порядке, что и в предыдущей задаче) области распределено следующим образом:
Постройте полигон частот и эмпирическую функцию распределения.
315. Количество учащихся, получивших аттестат с медалью, в 2001 году по городам и районам Ярославской области:
г. Ярославль — 280, г. Рыбинск — 66, г. Ростов — 61, г. Переславль — 27, г. Углич — 32, г. Тутаев — 36;
Большесельский — 8, Борисоглебский — 3, Брейтовский — 11, Гаврилов-Ямский — 7, Даниловский — 19, Любимский — 11, Мышкинский — 3, Некоузский — 15, Некрасовский — 7, Первомайский — 6, Переславский — 1, Пошехонский — 8, Ярославский — 30.
Найдите вариационный ряд распределения медалистов, размах варьирования и среднее число медалистов по городам и районам области.
316. Посевные площади картофеля (тыс. гектаров) в сельских хозяйствах Ярославской области по районам:
1,5; 1,5; 0,6; 1,3; 0,9; 0,9; 0,6; 1,3; 1,1; 0,6; 1,1; 0,9; 1,6; 1,3; 0,8; 0,4; 1,1.
Найдите статистический ряд распределения посевных площадей и постройте полигон относительных частот.
II. 317. Построить гистограмму выборки, представленной в виде таблицы частот. Объем выборки .
— Сумма частот вариант интервала
318. Построить гистограмму выборки объема , представленной в виде таблицы частот:
Источник
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more