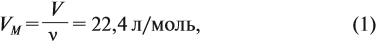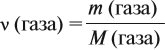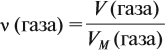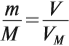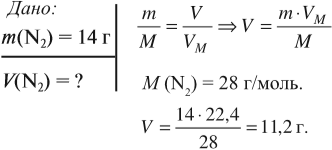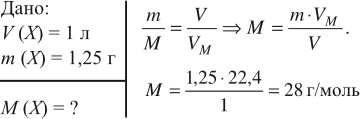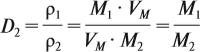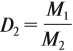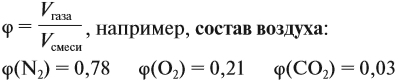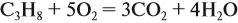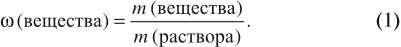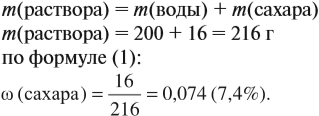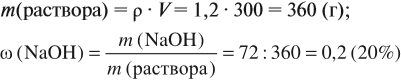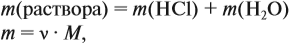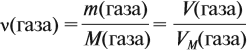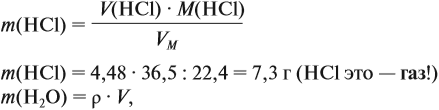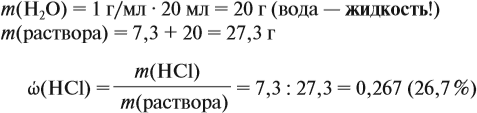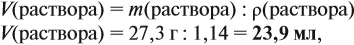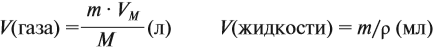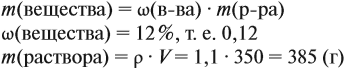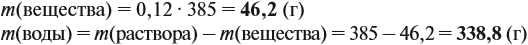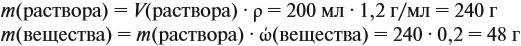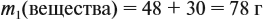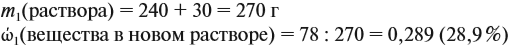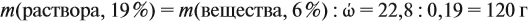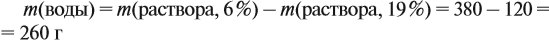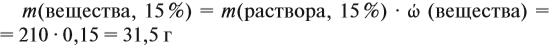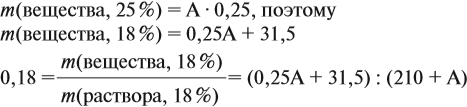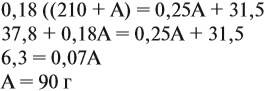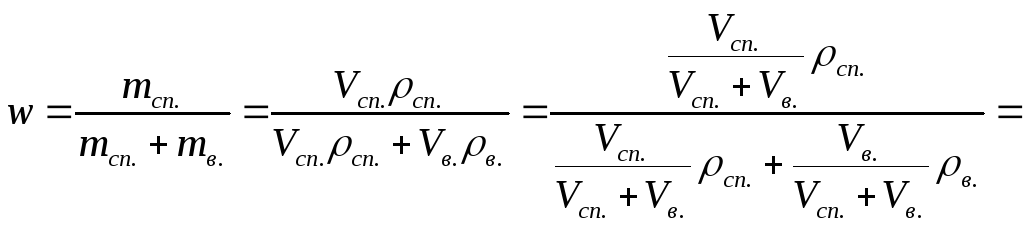Как найти плотность газа в растворе

В ходе решения таких задач рекомендуется придерживаться алгоритма:

• внимательно прочитать условие задачи и выяснить, что у вас спрашивают;
• написать соответствующую формулу и проанализировать её;
• найти числовые значения требуемых величин, каждый раз записывая вначале формулу, а затем расчёт, учитывая размерность величин.

Задачи по теме «Газы»

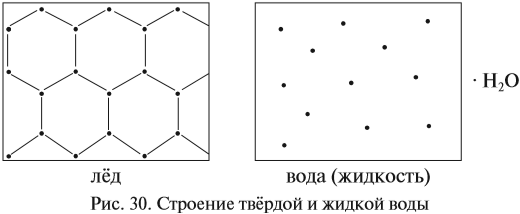
Известно, что вещества при нормальных условиях (н. у.) могут находиться в трёх агрегатных состояниях: твёрдом, жидком, газообразном. В твёрдом и жидком состояниях между молекулами (атомами) вещества имеются довольно сильные взаимодействия, в результате чего частицы находятся на небольших расстояниях друг от друга (рис. 30).

В газах расстояния между частицами очень велики, и силы взаимодействия ничтожны (рис. 31).

Поэтому равные объёмы любых газов содержат одинаковое число молекул. Это формулировка закона АВОГАДРО.

Следствием этого закона является:

1 моль любого газа при нормальных условиях (н. у.) занимает объём 22,4 литра.

Эта величина (22,4 л/моль) является молярным объёмом газа (V_М):

где V_M — молярный объём газа, моль/л; V — объём газа, л; ν — количество вещества газа, моль.

Таким образом, зная массу газа, можно определить:

Но для того же газа из формулы (1) имеем:

Отсюда для любого газа выполняется соотношение:

Задача 3. Какую массу имеет кислород объёмом 7 л?

Задача 4. Какой объём занимает азот массой 14 г?

Задача 5. Чему равна молярная масса газа, 1 л которого имеет массу 1,25 г?

Ответ. Молярная масса неизвестного газа 28 г/моль.

Пользуясь этими формулами, можно рассчитать объём, массу, молярную массу газа, например:

Известно, что

где ρ — плотность газа (г/л), поэтому:

ПОМНИТЕ! Эти формулы можно использовать лишь тогда, когда данные задачи (плотность газа, его объём) измерены при н. у.: 273 К, 1 атм.

Из формулы (3) вытекает понятие об относительной плотности газов (D_x). Эта величина, равная отношению плотностей двух газов:

где ρ₁ и М₁ — плотность и молярная масса одного газа, а ρ₂ и М₂ — плотность и молярная масса другого газа.

Относительная плотность газа показывает, во сколько раз данный газ тяжелее второго газа. Пользуясь этой формулой, можно легко определить молярную массу данного газа:

Выполняя такие расчёты, следует помнить, что:

• любая смесь газов, например воздух, именуется в задачах словом «газ»;
• средняя молярная масса воздуха, как показывают расчёты, равна 29 г/моль;
• по умолчанию, если не сказано иного, расчёты ведут для н. у.: 273 К, 1 атм.

Задача 6. Определить молярную массу газа, если:

а) плотность его равна 1,25 г/л;
б) плотность его по кислороду равна 0,75.

Решение.

Состав смеси газов, как правило, измеряют в объёмных процентах φ (фи).

Второе следствие, при помощи которого была экспериментально подтверждена гипотеза Авогадро (гипотеза стала законом уже после смерти автора!), заключается в следующем: объемы реагирующих газов относятся как их коэффициенты в соответствующем уравнении реакции.

Это следствие позволяет решать задачи «в уме», если известны объёмы реагирующих газов или количества вещества для них.

Задача 7. Какой объём кислорода потребуется для сжигания 6 л пропана?

Из уравнения реакции:

видно, что молярное соотношение пропана и кислорода составляет 1 : 5. Таким образом, объём кислорода в пять раз больше объёма пропана.

Ответ. Требуется 5 · 6 = 30 л кислорода.

Задачи для самостоятельного решения

3. Определить массы газов:

а) хлороводорода, объёмом 56 л;
б) озона О₃, объёмом 14 л.

4. Определить объёмы газов:

а) хлороводорода, массой 72 г;
б) аммиака NH₃, массой 3,4 г.

5. Определить молярные массы газов, если:

а) 2 л газа имеет массу 2,86 г;
б) 10 г газа занимает объём 7,47 л.

6. Определить молярную массу газа, если:

а) плотность его равна 1,52 г/л;
б) плотность по кислороду равна 1,81.

7. Какой объем занимает смесь, состоящая из 4 г метана и 22 г пропана?

8. Какой газ имеет большую массу: этан, объёмом 56 л или бутан, объёмом 44,8 л?

9. Существуют ли газообразные соединения серы легче воздуха?

10. Определите, не выполняя расчёт, какой из газов тяжелее воздуха: Не, Ar, CO₂, CH₄, N₂, O₂.

Задачи по теме «Способы выражения концентрации растворов»

Для того чтобы определить массовую долю растворенного вещества, нужно воспользоваться формулой:

Ответ может быть дан в долях (единицы): ω = 0,15; или в процентах: ω% = 15 %.

Задача 8. В 200 г воды растворили 16 г сахара. Определить ω(сахара) в полученном растворе.

Решение. В данном случае масса раствора неизвестна. Но:

Задача 9. В 300 мл раствора (ρ = 1,2 г/мл) содержится 72 г NаОН. Определить ω(NаОН) в этом растворе.

Решение. В этом случае масса раствора неизвестна, но известен объём. Найдём массу раствора:

Задача 10. В 20 мл воды растворили 4,48 л хлороводорода. Определить ω(НСl) в соляной кислоте. Плотность раствора равна 1,14 г/мл.

Решение. При растворении хлороводорода в воде получена соляная кислота, её масса равна:

где ν — количество вещества, моль; M — молярная масса вещества, причём для газов

откуда

где ρ — плотность воды (1 г/мл); V — объём воды, мл

Обратите внимание: в 20 мл воды растворили 4,48 л газа, но суммарный объём отнюдь не равен (4,48 + 0,02), т. е. 4,5 литра! Суммарный объём этого раствора равен:

т. е. при растворении более 4 литров газа объём жидкого раствора увеличился менее чем на 4 миллилитра!

Выводы.

1. Объёмы жидкостей и объёмы растворяемых газов суммировать нельзя.
2. При растворении в жидкости газы сжимаются более чем в 1000 раз.
3. Объёмы жидкостей и газов рассчитывают (исходя из значения массы) по-разному:

где m — масса, г; М — молярная масса, г/моль; V — объём (жидкости в мл, газа — в л); ρ — плотность жидкости, г/мл.

Пользуясь формулой (1) нетрудно рассчитать и массу раствора, и массу растворённого вещества. Но при этом следует учитывать, что обычно в задачах говорится (упоминается) о «5 %-ном растворе», «16 %-ном растворе» и т. д., т. е. массовая доля вещества выражена в процентах. В этом случае легко видеть, что:

• в 5 %-ном растворе ω(вещества) = 0,05;
• в 16 %-ном растворе ω(вещества)= 0,16 и т. д.

Зная массовую долю вещества в растворе, можно определить:

Задача 11. Сколько граммов соли и воды нужно взять для приготовления 350 мл (ρ = 1,1 г/мл) 12 %-ного раствора?

Решение. Из формулы (1) получаем формулу (2):

где ρ — плотность раствора (1,1 г/мл); V — объём раствора (350 мл), тогда

Задача 12. Сколько граммов 8 %-ного раствора можно приготовить, имея 64 г NaCl?

Решение. Из формулы (3):

Такие задачи можно решать, составляя пропорции. При этом следует знать, что массовая доля (в %) вещества показывает, сколько граммов вещества содержится (растворено) в 100 граммах раствора: 5 %-ный раствор ⇒ 5 г вещества в 100 граммах раствора.

Задача 13. Сколько мл 15 %-ного раствора (ρ = 1,1 г/мл) можно приготовить из 22,5 г вещества?

Обратите внимание: в пропорции в одном столбце должны совпадать и размерность, и наименование компонента, о котором идёт речь.

Задача 14. К 200 мл 20 %-ного раствора (ρ = 1,2 г/мл) добавили 30 г того же вещества. Определить массовую долю вещества в полученном растворе.

Решение. Определим в начале массу исходного раствора и растворённого вещества:

При добавлении новых порций растворяемого вещества, его масса увеличивается:

На ту же величину увеличивается масса раствора:

Задача 15. Сколько граммов 19 %-ного раствора и воды нужно взять для получения 380 г 6 %-ного раствора?

Решение. При добавлении воды масса растворённого вещества не меняется. Поэтому рассчитаем массу растворённого вещества в 6 %-ном растворе (столько же его будет и в 19 %-ном растворе):

Теперь можно рассчитать массу 19 %-ного раствора:

Теперь задумаемся: почему возросла масса исходного 19 %-ного раствора? Потому, что добавили воду. Значит, масса воды равна:

Ответ. Нужно добавить 260 г воды.

В случаях, когда изменяется и масса раствора, и масса вещества, нужно прибегнуть к приёму, когда неизвестная величина (о ней спрашивается в вопросе задачи), принимается за известную, и обозначается А.

Задача 16. Сколько граммов 25 %-ного раствора нужно добавить к 210 г 15 %-ного раствора, чтобы получить 18 %-ный раствор?

Решение. Пусть нужно добавить А граммов 25 %-ного раствора, тогда масса 18 %-ного раствора составит (210 + А) г. Определим массу вещества в 15 %-ном растворе:

аналогично:

Решим полученное уравнение:

Ответ. Нужно добавить 90 г 25 %-ного раствора.

Задачи для самостоятельного решения

11. В 300 г раствора содержится 45 г поваренной соли. Определить ω (NaСl) в этом растворе.

12. В 300 мл воды растворили 100 г сахара. Определить ω (сахара) в полученном растворе.

13. В 2 л раствора (пл. = 1,05 г/мл) содержится 105 г соли. Определить ω(соли) в этом растворе.

14. В 200 мл воды растворили 56 л аммиака NH₃. Определить ω (NH₃) в этом растворе.

15. Бромоводород объёмом 5,4 л затрачен на приготовление 8 %-ного раствора (пл. = 1,057 г/мл). Найти объём полученного раствора.

16. Сколько граммов воды и сахара нужно взять для приготовления 3 литров 30 %-ного сиропа? (Пл. = 1,13 г/мл.)

17. Какой объём 25 %-ного раствора можно приготовить из 150 г соли, если плотность раствора равна 1,2 г/мл?

18. К 500 мл 32 %-ной кислоты (ρ = 1,2 г/мл) добавили 1 л воды. Вычислить массовую долю кислоты в полученном растворе.

19. Смешали 25 г 16 %-ного раствора КОН с 30 мл 20 %-ного раствора КОН (плотность 1,2 г/мл). Вычислить массовую долю щёлочи в полученном растворе.

20. К 220 г 20 %-ного раствора поваренной соли добавили 44 мл воды и 36 г этой же соли. Вычислить массовую долю соли в полученном растворе.

21. Определить массу воды, которую нужно выпарить из 1 кг 3 %-ного раствора сульфата меди II для получения 5 %-ного раствора.

22. Сколько граммов воды нужно добавить к 50 г 70 %-ной уксусной кислоты, чтобы получить 5 %-ный уксус?

23. После добавления соды к 200 мл 16 %-ного раствора её (ρ = 1,17 г/мл) массовая доля вещества возросла до 20 %. Определить массу добавленной соды.

24. Какой объём 96 %-ной кислоты (ρ = 1,86 г/мл) необходимо добавить к 5 л 30 %-ной кислоты (ρ = 1,3 г/мл), для того чтобы получить 40 %-ный раствор?

Способы выражения состава.

Способ выражения состава	Обозначение содержания компонента А	Международные обозначения
Название величины	Значение величины	в жидкой фазе	в газовой фазе
Молярная доля		x	y	х, у
Массовая доля				w
Относительная молярная доля		X	Y	X, Y
Относительная массовая доля				W
Молярная концентрация		Cx	Cy	c
Массовая концентрация
Объёмная доля		xV	y	φ

Примечание:
объёмная доля для газов равна молярной
доле и обозначается y;
объёмная доля для жидкостей обозначается
также как и молярная доля х,
но, поскольку для жидкостей это разные
величины, в скобках делается пометка,
например х
= 10% (об.).
Допускается также использование нижнего
индекса х_v.

Расчёт плотности и вязкости.

Плотность газа при температуре Т
(К) и давлении р:

,
где.

Здесь Т₀ = 273 К,р₀
= 760 ммHg= 1,013·10⁵Па,V_m
= 22,4 м³/кмоль.

Плотность смеси газов:

.

Плотность смеси жидкостей:

;

формула плохо применима к смесям
жидкостей со значительным объёмным
эффектом смешения, таким как вода–этанол.

Плотность суспензий:

.

Вязкость газа при температуре Т
(К):

,

где С– постоянная Сатерленда [1,
табл.V].

Вязкость смеси газов:

.

Для коксового, генераторного и подобных
им газов:

,

где Т_{кр i}– критическая температураi-го
компонента, К [1, табл.XI].

Вязкость смеси жидкостей

через молярные доли:

;

через объёмные доли:

.

Вязкость суспензий:

при

;

при

.

Семинар 2.

Задача 1.

Определить объём воды и 96%-го (объёмные
%) раствора этанола необходимые для
получения 1 м³40%-го раствора
этанола. Температуру жидкостей принять
равной 20°С.

Дано: φн= 96% (об.), φк= 40% (об.), V40% = 1 м3, t= 20°C.

Найти: Vв ,V96% .

Схема аппарата:

Решение.

В зависимости от способа приготовление
растворов объёмные доли могут быть
рассчитаны по двум различным формулам:

(1) и(2)

Вторая формула применима к растворам,
приготовленным в лабораторных условиях,
когда определённый объём спирта
помещается в мерный цилиндр, а затем
объём доводится дистиллированной водой
до метки.

В промышленности, где имеют дело с
большими объёмами, применима первая
формула, которую мы и будем использовать
в дальнейших расчётах.

Выведем формулу для пересчёта объёмных
долей в массовые:

(3).

Аналогично могут быть получены формулы
для пересчёта массовых долей в молярные
и молярных долей в массовые, соответственно:

(4),(5).

Таблица пересчёта одних концентраций
в другие приведена в [1, с. 283, табл. 6.2], в
начале главы 6 «Основы массопередачи.
Абсорбция».

По формуле (3) производим пересчёт
объёмных долей в массовые для 40%-го и
96%-го растворов:

,.

Исходя из ближайших табличных значений
плотностей водных растворов этанола,
найдём плотности наших растворов методом
линейной интерполяции:

Плотности водных растворов этилового спирта при 20оС [1, табл.IV].
Масс. % спирта.	Плотность, кг/м3.
100	789
80	843
60	891
40	935
20	969
0	998

Из подобия большого и малого
(заштрихованного) треугольников получаем
соотношения:

;.

Следовательно, плотности 40 и 96%-ного
растворов соответственно равны:

,.

Рассчитаем массу 40%-го раствора этанола:

.

Рассчитаем массу этанола, содержащегося
в растворе:

.

Рассчитаем массовый расход 96%-го раствора
этанола:

.

Рассчитаем массу воды, необходимой для
разбавления 96%-го раствора:

.

Рассчитаем объём 96%-го раствора этанола:

.

Рассчитаем объём воды, необходимой для
разбавления 96%-го раствора:

.

Рассчитаем объёмный эффект смешения:

.

Задача 2.

При синтезе аммиака из водорода и азота
на выходе из реактора получают смесь,
содержащую 12% (об.) аммиака, 22% (об.) азота
и 66% (об.) водорода. Температура смеси
500°С, давление 30 МПа. Определить
плотности компонентов и плотность
смеси.

Расчеты массы (объема, количества вещества) продукта реакции, если одно из веществ дано в виде раствора с определенной массовой долей растворенного вещества

Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:

1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:

* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:

* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:

После чего следует рассчитать массу растворенного вещества по формуле 1.

2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:

3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.

4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:

Если  в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.

5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:

Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:

Рассмотрим пару примеров расчетных задач по этой теме.

Пример 1

Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.

Решение:

1) Рассчитаем массу чистой серной кислоты:

m(H₂SO₄) = w(H₂SO₄) ∙ m(р-ра H₂SO₄)/100% = 147 г ∙ 20% /100%  = 29,4 г

2) Рассчитаем количество вещества (моль) серной кислоты:

n(H₂SO₄) = m(H₂SO₄) / M(H₂SO₄) = 29,4 г/98 г/моль =  0,3 моль.

3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:

H₂SO₄ + Ba(NO₃)₂ = BaSO₄↓ + 2HNO₃

4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:

n(BaSO₄)/n(H₂SO₄) = k(BaSO₄)/k(H₂SO₄), где n — количество вещества, а k — коэффициент в уравнении реакции,

можем записать:

n(BaSO₄) = n(H₂SO₄) ∙ k(H₂SO₄)/k(BaSO₄) = 0,3 моль ∙ 1/1 = 0,3 моль

5) Тогда масса осадка, т.е. сульфата бария, может  быть рассчитана следующим образом:

m(BaSO₄) = M(BaSO₄) ∙ n(BaSO₄) = 233 г/моль ∙ 0,3 моль = 69,9 г

Пример 2

Какой объем газа (н.у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.

Решение:

1) Рассчитаем массу раствора соляной кислоты:

m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г

Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:

m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г

2) Рассчитаем количество вещества хлороводорода:

n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;

3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:

FeS + 2HCl = FeCl₂ + H₂S↑

4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:

n(HCl)/n(H₂S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и H₂S соответственно

Следовательно:

n(H₂S) = n(HCl)/2 = 0,5/2 = 0,25 моль

5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = V_m ∙ n(газа), тогда:

V(H₂S) = V_m ∙ n(H₂S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л

Автор: С.И. Широкопояс https://scienceforyou.ru/

Как определить плотность раствора

Раствор характеризуется объемом, концентрацией, температурой, плотностью и другими параметрами. Плотность раствора меняется в зависимости от массы и концентрации растворенного вещества.

Инструкция

Ключевой формулой для плотности является ρ=m/V, где ρ – плотность, m – масса раствора, V – его объем. Плотность может выражаться, например, в килограммах на литр, или в граммах на миллилитр. В любом случае, она показывает, сколько вещества по массе приходится на единицу объема.

Масса раствора складывается из массы жидкости и массы растворенного в ней вещества: m(раствора)=m(жидкости)+m(растворенного вещества). Масса растворенного вещества и объем раствора могут быть найдены из известного значения концентрации и молярной массы.

Пусть, например, в задаче дана молярная концентрация раствора. Она обозначается химической формулой соединения в квадратных скобках. Так, запись [KOH]=15 моль/л означает, что в одном литре раствора содержится 15 моль вещества гидроксида калия.

Молярная масса KOH составляет 39+16+1=56 г/моль. Молярные массы элементов можно посмотреть в таблице Менделеева, они указываются обычно снизу от наименования элемента. Количество вещества, масса вещества и его молярная масса связаны соотношением ν=m/M, где ν – количество вещества (моль), m – масса (г), M – молярная масса (г/моль).

Растворы, помимо жидкостных, бывают еще и газовыми. В этом случае необходимо понимать, что в равных объемах газа, близкого к идеальному, при одних и тех же условиях содержится одно и то же число молей. К примеру, при нормальных условиях один моль любого газа занимает объем Vm=22,4 л/моль, который назван молярным объемом.

В решении задачи на плотность газового раствора может понадобиться соотношение, устанавливающее связь между количеством вещества и объемом: ν=V/Vm, где ν – количество вещества, V – объем раствора, Vm – молярный объем, постоянная величина для данных условий. Как правило, в подобных задачах обговаривается, что условия являются нормальными (н.у.).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Здравствуйте!

Калькуляторы для расчета инженерных физических величин.

1. Плотность вещества

2. Плотности газов при стандартных условиях

3. Расчет массы по плотности и объему вещества.

4. Расчет объему по плотности и массы вещества.

5. Плотность жидкости при смешивании нескольких веществ

6. Расчет плотности смеси газов

7. Удельный вес вещества

8. Кинематическая вязкость вещества

9. Плотность воды от температуры

СЛЕВА ТАБЛИЧКИ ДЛЯ ВЫБОРА

В платных разделах сайта калькулятора можно посчитать один раз в день.

Новости

Корректировок калькулятора нет.

Плотность некоторых веществ:
Плотность поваренной соли 2,165 г/см³
Плотность этилового спирта 0,7893 г/см³
Плотность глюкозы 1,5620 г/см³
Плотность сахара 1,587 г/см³
Плотность аммиака 0.7723 (н.у.)
Плотность хлорида бария 3,92 (20 °C)
Плотность серной кислоты 1,8356 г/см³
Плотность соляной кислоты 1.19 г/см³
Плотность азотной кислоты 1,513 г/см³
Плотность уксусной кислоты 1,0492 г/см³
Плотность ортофосфорной кислоты 1,685 (жидк)
Плотность борной кислоты 1,435 (+15 °C)
Плотность бромоводородной кислоты газ (25 °C), 3,307 г/л, жидкий (−68 °C) 2,17 г/см³
Плотность гидроксида натрия 2,13 г/см³
Плотность гидроксида калия 2,044 г/см³
Плотность гидроксида бария 4,5 (20 °C)
Плотность гидроксида лития 1,46 (25 °C)