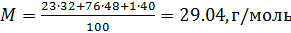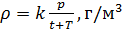Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
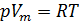
где:


R — универсальная газовая постоянная,
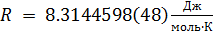
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём 
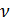
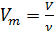
Также известно, что
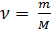
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
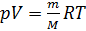
Как известно, плотность вещества

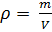
Из (4) и (5) выведем уравнение для плотности газа

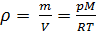
и введём обозначение параметра
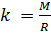
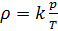
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
Молярные массы этих веществ воздуха будут соответственно равны:
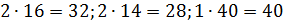
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
Теперь, зная значение константы

Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 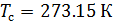
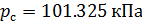
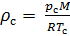
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 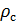
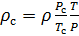
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 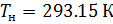
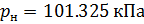

В уравнениях (10) и (11) используем значения параметров воздуха 
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.
Рис. 3 Система измерения давления и температуры
Листинг 1 — Программа опроса измерительного преобразователя давления и температуры
#include <SFE_BMP180.h>
SFE_BMP180 pressure;
double T,P;
void setup()
{
Serial.begin(9600);
pressure.begin();
}
void loop()
{
P = getPressure();
Serial.println(P+0.5, 2);
Serial.println(T+0.54, 2);
delay(1000);
}
double getPressure(){
char status;
status = pressure.startTemperature();
if (status != 0){
delay(status); // ожидание замера температуры
status = pressure.getTemperature(T);
if (status != 0){
status = pressure.startPressure(3);
if (status != 0){
delay(status); // ожидание замера давления
status = pressure.getPressure(P,T);
if (status != 0){
return(P);
}
}
}
}
}
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Листинг 2 – Определение плотности газа по результатам измерения давления и температуры
import numpy as np
import matplotlib.pyplot as plt
import serial
from drawnow import drawnow
import datetime, time
from pykalman import KalmanFilter
#вводим матрицу перехода и матрицу наблюдений
transition_matrix = [[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]]
observation_matrix = [[1, 0, 0, 0],
[0, 0, 1, 0]]
#вводим и инициируем матрицу измерений
initial_state_mean = [101000,
0,
28,
0]
#параметры уравнения состояния идеального газа:
#универсальная газовая постоянная R, [Дж/(моль*К)]
R = 8.314459848
#молярная масса воздуха M, [г/моль]
M = 29.04
#коэффициент k = M/R, [г/(Дж*К)]
k = M / R
#абсолютная температура, [K]
K = 273.16
#стандартное (нормальное) давление, [Па]
Pn = 101325
#определяем количество измерений
# общее количество измерений
str_m = input("введите количество измерений: ")
m = eval(str_m)
# количество элементов выборки
mw = 16
#настроить параметры последовательного порта
ser = serial.Serial()
ser.baudrate = 9600
port_num = input("введите номер последовательного порта: ")
ser.port = 'COM' + port_num
ser
#открыть последовательный порт
try:
ser.open()
ser.is_open
print("соединились с: " + ser.portstr)
except serial.SerialException:
print("нет соединения с портом: " + ser.portstr)
raise SystemExit(1)
#определяем списки
l1 = [] # для значений 1-го параметра
l2 = [] # для значений 2-го параметра
t1 = [] # для моментов времени
lw1 = [] # для значений выборки 1-го параметра
lw2 = [] # для значений выборки 2-го параметра
n = [] # для значений моментов времени
nw = [] # для значений выборки моментов времени
l1K = [] # для фильтрованных значений 1-го параметра
l2K = [] # для фильтрованных значений 2-го параметра
ro = [] # для плотности газовой среды
#подготовить файлы на диске для записи
filename = 'count.txt'
in_file = open(filename,"r")
count = in_file.read()
count_v = eval(count) + 1
in_file.close()
in_file = open(filename,"w")
count = str(count_v)
in_file.write(count)
in_file.close()
filename = count + '_' + filename
out_file = open(filename,"w")
#вывод информации для оператора на консоль
print("nпараметры:n")
print("n - момент времени, с;")
print("P - давление, Па;")
print("Pf - отфильтрованное значение P, Па;")
print("T - температура, град. С;")
print("Tf - отфильтрованное значение T, град. С;")
print("ro - плотность воздуха, г/м^3;")
print("nизмеряемые значения величин параметровn")
print('{0}{1}{2}{3}{4}{5}n'.format('n'.rjust(3),'P'.rjust(10),'Pf'.rjust(10),
'T'.rjust(10),'Tf'.rjust(10),'ro'.rjust(10)))
#считываение данных из последовательного порта
#накопление списков
#формирование текущей выборки
i = 0
while i < m:
n.append(i)
nw.append(n[i])
if i >= mw:
nw.pop(0)
ser.flushInput() #flush input buffer, discarding all its contents
line1 = ser.readline().decode('utf-8')[:-1]
line2 = ser.readline().decode('utf-8')[:-1]
t1.append(time.time())
if line1:
l = eval(line1)
#l = np.random.normal(l,100.0)
l1.append(l)
lw1.append(l1[i])
if i >= mw:
lw1.pop(0)
if line2:
l = eval(line2)
#l = np.random.normal(l,1.5)
l2.append(l)
lw2.append(l2[i])
if i >= mw:
lw2.pop(0)
#-------------------------
initial_state_mean = [l1[i],0,l2[i],0]
kf1 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean)
if i == 0:
measurements = np.array( [ [l1[i], l2[i]],
[initial_state_mean[0], initial_state_mean[2]] ] )
measurements = np.array( [ [l1[i], l2[i]],
[l1[i-1], l2[i-1]] ] )
kf1 = kf1.em(measurements, n_iter=2)
(smoothed_state_means, smoothed_state_covariances) = kf1.smooth(measurements)
l1K.append(smoothed_state_means[0, 0])
l2K.append(smoothed_state_means[0, 2])
#плотность воздуха в рабочих условиях
#ro.append( k * l1K[i]/( l2K[i] + K) )
#плотность воздуха, приведенная к стандартным условиям
ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/K/l1K[i]) )
#плотность воздуха, приведенная к нормальным условиям
#ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/(K+20)/l1K[i]) )
print('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
i += 1
ser.close()
time_tm = t1[m - 1] - t1[0]
print("nпродолжительность времени измерений: {0:.3f}, c".format(time_tm))
Ts = time_tm / (m - 1)
print("nпериод опроса датчика: {0:.6f}, c".format(Ts))
#запись таблицы в файл
print("nтаблица находится в файле {}n".format(filename))
for i in np.arange(0,len(n),1):
out_file.write('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}n'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
#закрыть файл с таблицей
out_file.close()
now = datetime.datetime.now() #получаем дату и время
#выводим графики
plt.figure('давление')
plt.plot( n, l1, "b-", n, l1K, "r-")
plt.ylabel(r'$давление, Па$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.figure('температура')
plt.plot( n, l2, "b-", n, l2K, "r-")
plt.ylabel(r'$температура, degree С$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.figure('плотность воздуха')
plt.plot( n, ro, "r-")
plt.ylabel(r'$плотность воздуха, г/м^3$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.show()
Результаты расчёта представлены листингом и рис. 4, 5, 6.
Интерфейс пользователя и таблица результатов расчёта
введите количество измерений: 33
введите номер последовательного порта: 6
соединились с: COM6
параметры:
n - момент времени, с;
P - давление, Па;
Pf - отфильтрованное значение P, Па;
T - температура, град. С;
Tf - отфильтрованное значение T, град. С;
ro - плотность воздуха, г/м^3;
измеряемые значения величин параметров
n P Pf T Tf ro
0 101141.000 101141.000 28.120 28.120 1295.574
1 101140.000 101140.099 28.190 28.183 1295.574
2 101140.000 101140.000 28.130 28.136 1295.574
3 101141.000 101140.901 28.100 28.103 1295.574
4 101140.000 101140.099 28.100 28.100 1295.574
5 101141.000 101140.901 28.110 28.109 1295.574
6 101141.000 101141.000 28.100 28.101 1295.574
7 101139.000 101139.217 28.100 28.100 1295.574
8 101138.000 101138.099 28.090 28.091 1295.574
9 101137.000 101137.099 28.100 28.099 1295.574
10 101151.000 101149.028 28.100 28.100 1295.574
11 101136.000 101138.117 28.110 28.109 1295.574
12 101143.000 101142.052 28.110 28.110 1295.574
13 101139.000 101139.500 28.100 28.101 1295.574
14 101150.000 101148.463 28.110 28.109 1295.574
15 101154.000 101153.500 28.120 28.119 1295.574
16 101151.000 101151.354 28.110 28.111 1295.574
17 101141.000 101142.391 28.130 28.127 1295.574
18 101141.000 101141.000 28.120 28.121 1295.574
19 101142.000 101141.901 28.110 28.111 1295.574
20 101141.000 101141.099 28.120 28.119 1295.574
21 101142.000 101141.901 28.110 28.111 1295.574
22 101146.000 101145.500 28.120 28.119 1295.574
23 101144.000 101144.217 28.130 28.129 1295.574
24 101142.000 101142.217 28.130 28.130 1295.574
25 101142.000 101142.000 28.140 28.139 1295.574
26 101142.000 101142.000 28.130 28.131 1295.574
27 101146.000 101145.500 28.150 28.147 1295.574
28 101142.000 101142.500 28.190 28.185 1295.574
29 101146.000 101145.500 28.230 28.225 1295.574
30 101146.000 101146.000 28.230 28.230 1295.574
31 101146.000 101146.000 28.220 28.221 1295.574
32 101150.000 101149.500 28.210 28.211 1295.574
продолжительность времени измерений: 6.464, c
период опроса датчика: 0.201998, c
таблица находится в файле 68_count.txt
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Ссылки на источники информации
- ГОСТ 8.586.5-2005. URL
- ГОСТ Р 8.740 – 2011. URL
- Ideal gas law. URL
- Standard conditions for temperature and pressure. URL
Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.
Идеальный газ
Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:
- пренебрежение размерами молекул;
- силы молекулярного взаимодействия не учитываются;
- соударение атомов и молекул абсолютно упруго;
- газ находится в термодинамическом равновесии.
Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.
Газовые законы
Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:
- при постоянном давлении уменьшить температуру;
- при постоянной температуре увеличить давление.
Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.
В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.
Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.
Комбинированный закон
Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:
где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.
Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.
Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.
Пример использования калькулятора
Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.
Заключение
Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
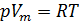


R — универсальная газовая постоянная,
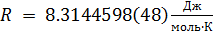
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём 
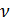
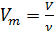
Также известно, что
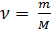
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
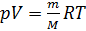
Как известно, плотность вещества

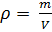
Из (4) и (5) выведем уравнение для плотности газа

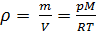
и введём обозначение параметра
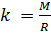
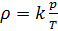
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
Молярные массы этих веществ воздуха будут соответственно равны:
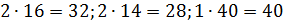
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
Теперь, зная значение константы
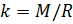

Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 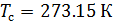
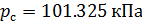
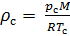
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 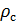
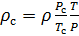
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 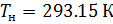
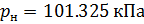

В уравнениях (10) и (11) используем значения параметров воздуха 
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
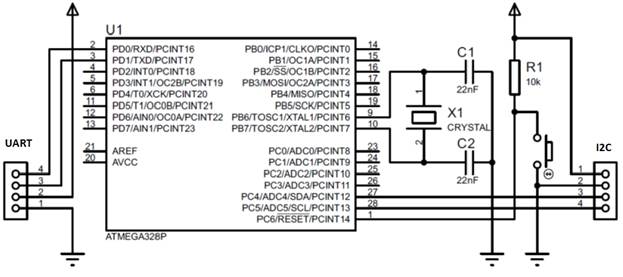
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Результаты расчёта представлены листингом и рис. 4, 5, 6.
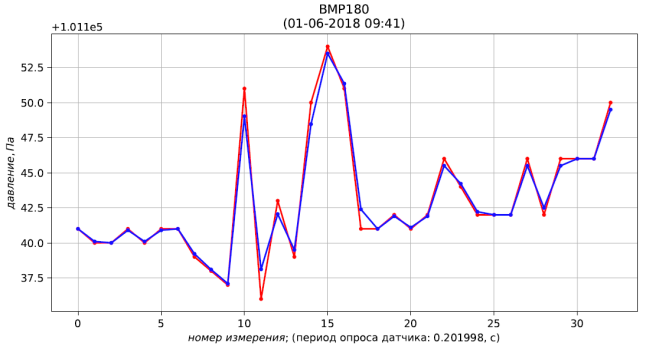
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
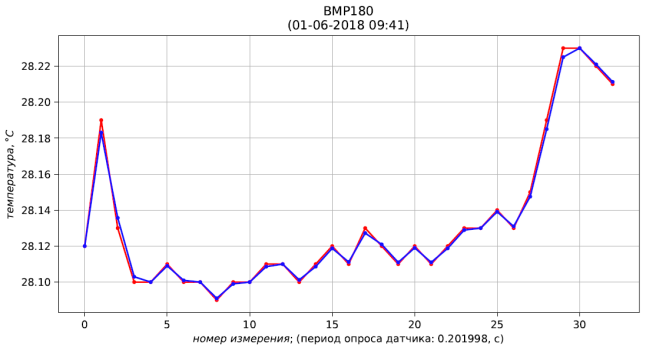
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Density is mass per unit volume. Finding the density of a gas is the same as finding the density of a solid or liquid. You have to know the mass and the volume of the gas. The tricky part with gases is that you are often given pressures and temperatures with no mention of volume. You have to figure it out from the other information.
How to Find Density of a Gas
- Calculating the density of a gas usually involves combining the formula for density (mass divided by volume) and the ideal gas law (PV = nRT).
- ρ = PM/RT, where M is molar mass.
- The ideal gas law is a good approximation of the behavior of real gases.
- Usually, with this type of problem, you are given the type of gas and enough other variables to solve the ideal gas law problem.
- Remember to convert temperature to absolute temperature and watch your other units.
Density of a Gas Example Calculation
This example problem will show how to calculate density of a gas when given the type of gas, the pressure, and the temperature.
Question: What is the density of oxygen gas at 5 atm and 27 °C?
First, let’s write down what we know:
Gas is oxygen gas or O2.
Pressure is 5 atm
Temperature is 27 °C
Let’s start with the Ideal Gas Law formula.
PV = nRT
where
P = pressure
V = volume
n = number of moles of gas
R = gas constant (0.0821 L·atm/mol·K)
T = absolute temperature
If we solve the equation for volume, we get:
V = (nRT)/P
We know everything we need to find the volume now except the number of moles of gas. To find this, remember the relationship between number of moles and mass.
n = m/MM
where
n = number of moles of gas
m = mass of gas
MM = molecular mass of the gas
This is helpful since we needed to find the mass and we know the molecular mass of oxygen gas. If we substitute for n in the first equation, we get:
V = (mRT)/(MMP)
Divide both sides by m:
V/m = (RT)/(MMP)
But density is m/V, so flip the equation over to get:
m/V = (MMP)/(RT) = density of the gas.
Now we need to insert the values we know.
MM of oxygen gas or O2 is 16+16 = 32 grams/mole
P = 5 atm
T = 27 °C, but we need absolute temperature.
TK = TC + 273
T = 27 + 273 = 300 K
m/V = (32 g/mol · 5 atm)/(0.0821 L·atm/mol·K · 300 K)
m/V = 160/24.63 g/L
m/V = 6.5 g/L
Answer: The density of the oxygen gas is 6.5 g/L.
Another Example
Calculate the density of carbon dioxide gas in the troposphere, knowing the temperature is -60.0 °C and the pressure is 100.0 millibar.
First, list what you know:
- P = 100 mbar
- T = -60.0 °C
- R = 0.0821 L·atm/mol·K
- carbon dioxide is CO2
Right off the bat, you can see some units don’t match up and that you need to use the periodic table to find the molar mass of carbon dioxide. Let’s start with that.
- carbon mass = 12.0 g/mol
- oxygen mass = 16.0 g/mol
There is one carbon atom and two oxygen atoms, so the molar mass (M) of CO2 is 12.0 + (2 x 16.0) = 44.0 g/mol
Converting mbar to atm, you get 100 mbar = 0.098 atm. Converting °C to K, you get -60.0 °C = 213.15 K.
Finally, all of the units agree with those found in the ideal gas constant:
- P = 0.98 atm
- T = 213.15 K
- R = 0.0821 L·atm/mol·K
- M = 44.0 g/mol
Now, plug the values into the equation for the density of a gas:
ρ = PM/RT = (0.098 atm)(44.0 g/mol) / (0.0821 L·atm/mol·K)(213.15 K) = 0.27 g/L
Sources
- Anderson, John D. (1984). Fundamentals of Aerodynamics. McGraw-Hill Higher Education. ISBN 978-0-07-001656-9.
- John, James (1984). Gas Dynamics. Allyn and Bacon. ISBN 978-0-205-08014-4.
- Khotimah, Siti Nurul; Viridi, Sparisoma (2011). «Partition function of 1-, 2-, and 3-D monatomic ideal gas: A simple and comprehensive review». Jurnal Pengajaran Fisika Sekolah Menengah. 2 (2): 15–18.
- Sharma, P. V. (1997). Environmental and Engineering Geophysics. Cambridge University Press. ISBN 9781139171168. doi:10.1017/CBO9781139171168
- Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. ISBN 978-0-321-69686-1.
Плотность газа при заданном давлении и температуре газа Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Молярная масса: 44.01 Грамм на моль —> 0.04401 Килограмм на моль (Проверьте преобразование здесь)
Давление газа: 0.215 паскаль —> 0.215 паскаль Конверсия не требуется
Температура газа: 45 Кельвин —> 45 Кельвин Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2.5289668094834E-05 Килограмм на кубический метр —>2.5289668094834E-05 Грамм на литр (Проверьте преобразование здесь)
Плотность газа при заданном давлении и температуре газа формула
Плотность газа = (Молярная масса*Давление газа)/([R]*Температура газа)
ρgas = (Mmolar*Pgas)/([R]*Tg)
Плотность — физическое свойство газа
Плотность газа r вычисляют по формуле ( по ГОСТ 30319.1-96)
r = т/V.
Плотность определяют с помощью плотномеров любого типа (пикнометрических, ареометрических, вибрационных, акустических, радиационных и др.) или косвенным методом (измерением параметров состояния среды, определения ее состава и проведения расчета).
В зависимости от технико-экономической целесообразности плотность контролируемых сред допускается рассчитывать:
- вручную,
- с помощью таблиц и графиков,
- с применением вычислительных машин;
- частично или полностью автоматизированных устройств.
Плотность газа в идеально газовом состоянии определяют по известным значениям давления р и температуры Т по формуле
rи = 103 × M × p/(R × T).
За молярную массу М принимают массу одного киломоля вещества в килограммах.
Молярную массу определяют по формуле
,
где Аj — масса килограмм-атома j-го элемента, входящего в состав молекулы;
пj — количество атомов j-го элемента молекулы.
3.2.2 Плотность реального газа (далее — газ) определяют с учетом фактора сжимаемости газа z по формуле
.
Плотность газа при стандартных условиях определяется при р = рc и Т = Тc т.е. по соотношению
.