Плотность — намотка
Cтраница 3
Коэффициент плотности намотки нити в бобине выражается отношением кажущейся плотности материала бобины к плотности элементарных нитей.
[31]
Под плотностью намотки понимают величину удельного давления между витками провода, а также между проводом и поверхностью каркаса.
[32]
Следовательно, плотность намотки витков должна подчиниться косинусоидальному закону распределения. На рис. 8.6 показана форма отклоняющих катушек. Для уменьшения влияния краевых полей края катушек отгибаются.
[33]
Задача 3.20. Плотность намотки витков катушки составила 10 витков на 1 см. Добавлением числа витков плотность намотки доведена до 15 витков на 1 см. Во сколько раз увеличится сопротивление и индуктивность катушки, если считать диаметр добавленных витков, материал и площадь поперечного сечения проволоки прежними.
[34]
При изменении плотности намотки изменяется только число витков.
[35]
При этом повышается плотность намотки и при оплетке лентой снижаются утолщения ленты по внутренним углам галет. Получаемые окна между гильзой и обмог-кой могут быть использованы для прохода внутренних выводов обмоток.
[36]
Для равномерной по плотности намотки пленок в рулоны применяют устройства с периферийным и центральным приводами. Намоточные устройства с периферийным приводом просты по конструкции, компактны и служат обычно для намотки эластичных пленок со скоростью до 30 м / мин. Устройство состоит из приводного барабана, по торцам которого установлены наклонные рейки. По рейкам может перемещаться штанга с шестернями на концах. Пленка наматывается на закрепленную на штанге бобину вследствие фрикционного сцепления наматываемой пленки, бобины и приводного вала. По мере увеличения диаметра рулон пленки откатывается по рейке от приводного вала, сохраняя с ним постоянный контакт, обеспечивающий непрерывную намотку рулона до необходимого размера. Недостатки устройств с периферийным приводом — затрудненные операции резки пленки, перезаправки и смены рулонов, особенно при скоростях намотки более 15 м / мин.
[38]
В целях сохранения плотности намотки лент в процессе работы кабеля ( при нагреве) накладывают бандажи из шпагата 15 и 19 поверх части обмотки 12 на длине трубчатой части наконечников с захватом участков замков и части поясной обмотки / Л Бандаж 19 накладывают на длине, равной примерно двукратному диаметру заделки в корешке, и располагают симметрично ( вверх и вниз) от среза оболочки кабеля.
[39]
При нарушении регулировки плотности намотки фильтрующего материала регулируют ее. Плотность намотки фильтрующего материала на нижние катушки регулируется фрикционной муфтой. Поворот гайки фрикционной муфты по ( против) часовой стрелке увеличивает ( уменьшает) передаваемый крутящий момент, а, следовательно, и натяжение материала. Фильтрующий материал должен наматываться на нижние катушки с уплотнением, не вызывающим разрушение материала. Проскальзывание фильтрующего материала по решеткам не допускается.
[40]
Коэффициент 1 25 учитывает плотность намотки. Прибавление к результату величины от 1 до 3 мм учитывает место, занимаемое прокладками. В случае обмотки с большим количеством слоев следует прибавлять к результату 2 — 3 мм, при небольшом числе витков достаточно прибавить 1 мм.
[41]
Коэффициент 1 25 учитывает плотность намотки. Прибавление к результату величины от 1 до 3 мм учитывает место, занимаемое прокладками. Если в обмотке большое количество слоев, следует прибавлять к результату 2 — 3 мм, при небольшом числе витков достаточно прибавить 1 мм.
[42]
В длинном соленоиде с плотностью намотки п вдали от его концов расположен намагниченный стержень, имеющий магнитный момент рм, ориентированный вдоль оси соленоида.
[43]
При переработке бобин с очень малой плотностью намотки ( рыхлых бобин) наблюдаются слеты витков нити при перемотке, что приводит к повышению обрывности; при переработке бобин с неравномерной плотностью намотки изготовленная ткань неравномерно окрашивается; в ней появляются стяжки и полосатость, а штучные изделия ( например, чулки) получаются различной длины.
[45]
Страницы:
1
2
3
4
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
НИТИ ХИМИЧЕСКИЕ
МЕТОД ОПРЕДЕЛЕНИЯ ПЛОТНОСТИ И ТВЕРДОСТИ НАМОТКИ
ГОСТ 11307-65
БЗ 8—95
Издание официальное
ИПК ИЗДАТЕЛЬСТВО СТАНДАРТОВ Москва
УДК 677.4.001.4:006.354 Групп» М99
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
НИТИ ХИМИЧЕСКИЕ
Метод определения плотности
и твердости намотки I ОС I
11307-65
Kemical fried. Method of the tarmination of windey density
Д«т» введения 1.07.66
Настоящий стандарт распространяется на химические нити в бобинах и устанавливает метод определения плотности и твердости намотки.
(Измененная редакция, Изм. № 2, 3).
1. МЕТОД ОТБОРА ПРОБ
1.1. Отбор проб — по ГОСТ 6611.0 со следующим дополнением: для проведения испытаний отбирают 10 бобин. Бобины должны быть правильной геометрической формы без повреждений и вмятин.
(Измененная редакция, Изм. Ns 2).
2. АППАРАТУРА
2.1. Для проведения испытания применяют:
весы, обеспечивающие погрешность взвешивания не более 1 % от взвешиваемой массы по ГОСТ 24104;
линейку по ГОСТ 427, штангенциркуль по ГОСТ 166 или устройство для определения размеров бобин, обеспечивающие погрешность измерения не более ±1 мм.
(Измененная редакция, Изм. № 2, 3).
Издание официальное Перепечатка воспрещена
© ИПК Издательство стандартов, 1996 Переиздание с изменениями
ГОСТ 11307-65 С. 2
3. ПОДГОТОВКА К ИСПЫТАНИЮ
3.1. Отобранные бобины перед испытанием выдерживают в климатических условиях по ГОСТ 10681. В этих же условиях проводят испытание. Длительность выдерживания перед испытанием по ГОСТ 6611.1.
(Измененная редакция, Изм. N° 2).
4. ПРОВЕДЕНИЕ ИСПЫТАНИЯ
4.1. Определение плотности намотки
4.1.1. Каждую бобину в отдельности взвешивают с погрешностью не более 1 % от взвешиваемой массы.
Параллельно определяют массу 10 патронов с погрешностью не более 1 % от взвешиваемой массы.
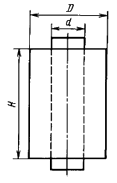
4.1.2. Линейные размеры бобины и патрона измеряют в точках, указанных на черт. 1—4, с погрешностью ±1 мм.
С. 3 ГОСТ 11307-65
(Измененная редакция, Изм. № 2, 3).
4.1.3. При использовании линейки допускается вместо измерения высот (Я, h, hu Л2) проводить измерение соответствующих образующих (L, /, /„ (j).
(Измененная редакция, Изм. № 2).
4.2 — 4.2.5 (Исключены, Изм. № 3).
5. ОБРАБОТКА РЕЗУЛЬТАТОВ
5.1. Плотность намотки (Я) в г/см3 вычисляют по формуле
где М — средняя масса нити в бобине, г;
Ун — средний объем намотки нити, см3.
Вычисление проводят с точностью до третьего десятичного знака с последующим округлением до второго десятичного знака.
5.1.1. Среднюю массу нити в бобине (М) в граммах вычисляют по формуле
М= тх~ т2, где /и, — средняя масса бобины, г; т2 — средняя масса патрона, г.
5.1.2. Средний объем намотки нити в бобине (Кн) в см3 вычисляют по формулам:
в цилиндрических бобинах (см. черт. 1)
Тг х Я (Д3 — rf2) н» 4 ■ 103
где Я — средняя высота патрона, занятого нитью, мм;
D— средний диаметр бобины, мм; d — средний диаметр патрона, мм;
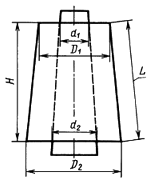
в одноконусных бобинах (см. черт. 2)
К = —3<D} + Dt— D2 + D-d-drd-d)*
ун = (ff+а • ц+з .
где Я, — средний диаметр верхнего основания бобины, мм;
D2 — средний диаметр нижнего основания бобины, мм;
ГОСТ 11307-65 С. 4
d, — средний диаметр патрона у верхнего основания бобины, мм; d2 — средний диаметр патрона у нижнего основания бобины, мм; L — средняя образующая бобины, мм;
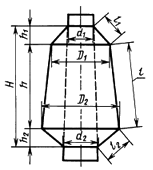
в трехконусных бобинах (см. черт. 3)
K = —^[hl(D} + ~dl Dl + d~] )+h(D}+DrD2 + D~l) +
+ Л2( D+ Z) 2 • </2 + d ) — H( d] + rf, • d2 + d )) и
■(Di + ~drDl + d~*) +
+ i П — 0,2S(D2 — Ъ,У ■ ( D] + D, Ъ2 + Z>j) + ]| T — 0,25 <D2 — x
*(D+D2 d2 + d) — Ц7 -ОЛЩ-d^ (rf + drd2 + d$) | ,
где Л, — средняя высота верхнего конуса бобины, мм;
А — средняя высота среднего конуса бобины, мм;
Л2 — средняя высота нижнего конуса бобины, мм;
— средний диаметр патрона у верхнего основания верхнего конуса бобины, мм;
d2 — средний диаметр патрона у нижнего основания конуса бобины, мм;
Z), — средний диаметр верхнего основания среднего конуса бобины, мм;
D2 — средний диаметр нижнего основания среднего конуса бобины, мм;
_/, — средняя образующая верхнего конуса бобины, мм;
— средняя образующая нижнего конуса бобины, мм;
/ — средняя образующая среднего конуса бобины, мм;
I — средняя образующая патрона, занятого нитью, мм;
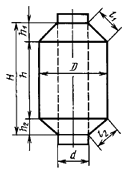
в биноконусных бобинах (см. черт. 4)
Кн = —^~г А.( D2 + d D+ d2) + —A Z)2 + н 12 I03 1 ‘ 4 10*
12 Ю3 2 ‘ 4 I03
12 103
К. = .(D2 + Dd+d2)+j^hD2 +
С. 5 ГОСТ 11307-65
Л/2— 0.25(0 ‘(D2 + D.d+d2)_±Jl.d2
+ 12. 1()3 4-10»
где_5 — средний диаметр патрона, мм;
D — средний диаметр бобины, мм.
5.1 —5.1.2. (Измененная редакция, Изм. № 2).
5.2. (Исключен, Изм. № 3).
Разделы 6 и 7 (Исключены, Изм. № 2).
Приложения 1—8 (Исключены, Изм. № 2). Приложение 9 (Исключено, Изм. № 3).
ГОСТ 11307-65 С. 6
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Министерством химической промышленности СССР
РАЗРАБОТЧИКИ
В.П. Галицин, канд.хим.наук; Ю.А. Толкачев; Л.А. Гордеева, канд.техн.наук; Л.В. Жир
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ ПОСТАНОВЛЕНИЕМ Государственного комитета стандартов, мер и измерительных приборов СССР от 12.07.65
3. Периодичность проверки — 5 лет
4. ВЗАМЕН ГОСТ 8871-58 в части п. 53-56
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер пункта |
|
ГОСТ 166-89 |
2.1 |
|
ГОСТ 427-75 |
2.1 |
|
ГОСТ 6611.0-73 |
1.1 |
|
ГОСТ 6611.1-73 |
3.1 |
|
ГОСТ 10681-75 |
3.1 |
|
ГОСТ 24104-88 |
2.1 |
6. Ограничение срока действия снято Постановлением Госстандарта от
30.03.92 № 312
7. ПЕРЕИЗДАНИЕ (сентябрь 1996 г.) с Изменениями № 1, 2, 3, утвержденными в июле 1973 г., августе 1981 г., марте 1992 г. (ИУС 8-73, 10-81, 6-92)
Редактор Р.Г Гнер<кмская Технический редактор В.И.Прусаком Корректор М С.Кабашола Компьютерная верстка А. Н. Золотаревой
Изд. лиц. №021007 от 10.08.95. Сдано в набор 19.11.96. Подписано в печать 15.11%. _Усл.печ.л. 0,47. Уч.-издл. 0,37. Тираж 148 экз. С 4131 За*. 668._
И ПК Издательство стандартов 107076, Москва, Колодезный пер., 14.
Набрано в Издательстве на ПЭВМ Филиал И ПК Издательство стандартов — тип. “Московский печатник» Москва, Лялин пер., 6

- Подробности
- Категория: Учеба
Страница 20 из 37
Площадь сечения катушки, перпендикулярного к направлению обмоточных проводов, непосредственно занятая обмоточными проводами, называется обмоточным пространством катушки (рис. 8.6) и равно
(8.1) где h — высота обмоточного пространства; а — ширина обмоточного пространства.
Если Dвн — внутренний диаметр обмотки катушки, а Dнар — ее наружный диаметр, то
(8-2)
Обычно рекомендуется соотношение высоты обмоточного пространства к его ширине h/a=(2-6), но это соотношение не является обязательным.
Использование обмоточного пространства будет тем лучше, чем большая часть его заполнена чистой медью. Эта величина характеризуется коэффициентом заполнения катушки по меди, который равен отношению площади, занятой медью, к площади обмоточного пространства:
(8.3)
Поскольку в качестве обмоточного провода в большинстве случаев применяется провод круглого сечения, то сечение меди одного провода q=πd2/4, где d — диаметр медной жилы провода; площадь катушки, занятая медью, если катушка имеет w витков, SM= (nd2/4)w.

Рис. 8.6. Обмоточное пространство катушки и укладка обмоточного провода:
а — рядовая; б — шахматная
Подставляя это выражение в (8.3) и учитывая (8.1), получим
(8.4)
Совершенно очевидно, что значение коэффициента заполнения по меди желательно иметь наибольшим. Величина коэффициента заполнения по меди зависит от следующих факторов:
- профиля медной жилы. Обмотка катушки, выполненная из прямоугольного обмоточного провода, будет иметь более высокое значение kз.м, так как прямоугольный провод можно уложить более плотно, чем круглый;
- толщины изоляции обмоточного провода. Чем толще изоляция, тем меньшую площадь занимает медь и тем ниже значение kз.м. Обычно принимается: для обмоточных проводов с эмалевой изоляцией kз.м.= (0,45-0,55); для проводов с изоляцией из пряжи и с комбинированной изоляцией kз.м=(0,28-0,35);
- сечения обмоточного провода. Чем больше сечение, тем выше значение kэ.м. Это объясняется не только тем, что провод крупного сечения можно уложить более плотно, но и тем, что радиальная толщина изоляции меняется незначительно при изменении диаметра провода, и для тонких проводов по отношению к сечению меди занимает большую площадь;
- способа намотки. Различают три способа намотки: рядовая (рис. 8.6, а), когда витки одного слоя располагаются достаточно плотно друг к другу и находятся точно над витками предыдущего слоя — наиболее распространенный способ; шахматная (рис. 8.6,б), когда витки слоя расположены в промежутках между витками предыдущего слоя — способ очень трудоемкий в изготовлении; когда витки хотя и расположены слоями, но точной укладки их не производится — применяется в катушках с большим числом витков из провода малого диаметра (0,14-0,3 мм).
В зависимости от способа намотки меняется ее плотность, а следовательно, меняется и значение kз.м. Наибольшую плотность и наибольшее значение kз.м. имеет шахматная обмотка, но из-за большой трудоемкости она почти не применяется. Наименьшую плотность и наименьшее значение kз.м. имеет дикая намотка, поскольку выполнить рядовую намотку при очень малых диаметрах обмоточного провода практически невозможно из-за огромной трудоемкости.
Величиной, характеризующей плотность намотки и возможность ее изготовления, является обмоточный коэффициент заполнения
(8.5)
В зависимости от способа намотки значение обмоточного коэффициента заполнения следующее: дикая обмотка kз.об.=0,6-0,75; рядовая обмотка kз.об.= 0,75-0,85; шахматная обмотка kз.об.=0,85 -0,95. При очень тщательной укладке витков достаточно большого диаметра (больше 1 мм) при рядовой, обмотке можно получить kз.об.=0,9-0,95. Обмоточный коэффициент заполнения при выполнении обмотки из меди прямоугольного сечения kз.об.=0,94-0,93.
Еще по теме:
Текст ГОСТ 11307-65 Нити химические. Метод определения плотности намотки
ГОСТ 11307-65
Группа М99
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
НИТИ ХИМИЧЕСКИЕ
Метод определения плотности и твердости намотки
Kemical fried. Method of the tarmination of windey density
Дата введения 1966-07-01
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Министерством химической промышленности СССР
РАЗРАБОТЧИКИ
В.П.Галицин, канд. хим. наук; Ю.А.Толкачев; Л.А.Гордеева, канд. техн. наук; Л.В.Жир
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ ПОСТАНОВЛЕНИЕМ Государственного комитета стандартов, мер и измерительных приборов СССР от 12.07.65
3. Периодичность проверки — 5 лет
4. ВЗАМЕН ГОСТ 8871-58 в части п.53-56
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер пункта |
|
ГОСТ 166-89 |
2.1 |
|
ГОСТ 427-75 |
2.1 |
|
ГОСТ 6611.0-73 |
1.1 |
|
ГОСТ 6611.1-73 |
3.1 |
|
ГОСТ 10681-75 |
3.1 |
|
ГОСТ 24104-88 |
2.1 |
6. Ограничение срока действия снято Постановлением Госстандарта от 30.03.92 N 312
7. ПЕРЕИЗДАНИЕ (сентябрь 1996 г.) с Изменениями N 1, 2, 3, утвержденными в июле 1973 г., августе 1981 г., марте 1992 г. (ИУС 8-73, 10-81, 6-92)
Настоящий стандарт распространяется на химические нити в бобинах и устанавливает метод определения плотности и твердости намотки.
(Измененная редакция, Изм. N 2, 3).
1. МЕТОД ОТБОРА ПРОБ
1.1. Отбор проб — по ГОСТ 6611.0 со следующим дополнением: для проведения испытаний отбирают 10 бобин. Бобины должны быть правильной геометрической формы без повреждений и вмятин.
(Измененная редакция, Изм. N 2).
2. АППАРАТУРА
2.1. Для проведения испытания применяют:
весы, обеспечивающие погрешность взвешивания не более 1% от взвешиваемой массы по ГОСТ 24104;
линейку по ГОСТ 427, штангенциркуль по ГОСТ 166 или устройство для определения размеров бобин, обеспечивающие погрешность измерения не более ±1 мм.
(Измененная редакция, Изм. N 2, 3).
3. ПОДГОТОВКА К ИСПЫТАНИЮ
3.1. Отобранные бобины перед испытанием выдерживают в климатических условиях по ГОСТ 10681. В этих же условиях проводят испытание. Длительность выдерживания перед испытанием по ГОСТ 6611.1.
(Измененная редакция, Изм. N 2).
4. ПРОВЕДЕНИЕ ИСПЫТАНИЯ
4.1. Определение плотности намотки
4.1.1. Каждую бобину в отдельности взвешивают с погрешностью не более 1% от взвешиваемой массы.
Параллельно определяют массу 10 патронов с погрешностью не более 1% от взвешиваемой массы.
4.1.2. Линейные размеры бобины и патрона измеряют в точках, указанных на черт.1-4, с погрешностью ±1 мм.
|
|
|
|
Черт.1 |
Черт.2 |
|
|
|
|
Черт.3 |
Черт.4 |
(Измененная редакция, Изм. N 2, 3).
4.1.3. При использовании линейки допускается вместо измерения высот (,
,
,
) проводить измерение соответствующих образующих (
,
,
,
).
(Измененная редакция, Изм. N 2).
4.2-4.2.5 (Исключены, Изм. N 3).
5. ОБРАБОТКА РЕЗУЛЬТАТОВ
5.1. Плотность намотки () в г/см
вычисляют по формуле
,
где — средняя масса нити в бобине, г;
— средний объем намотки нити, см
.
Вычисление проводят с точностью до третьего десятичного знака с последующим округлением до второго десятичного знака.
5.1.1. Среднюю массу нити в бобине () в граммах вычисляют по формуле
,
где — средняя масса бобины, г;
— средняя масса патрона, г.
5.1.2. Средний объем намотки нити в бобине () в см
вычисляют по формулам:
в цилиндрических бобинах (см. черт.1)
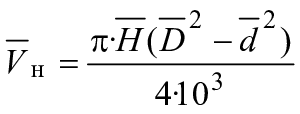
где — средняя высота патрона, занятого нитью, мм;
— средний диаметр бобины, мм;
— средний диаметр патрона, мм;
в одноконусных бобинах (см. черт.2)
и
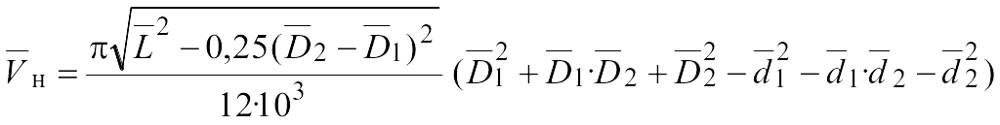
где — средний диаметр верхнего основания бобины, мм;
— средний диаметр нижнего основания бобины, мм;
— средний диаметр патрона у верхнего основания бобины, мм;
— средний диаметр патрона у нижнего основания бобины, мм;
— средняя образующая бобины, мм;
в трехконусных бобинах (см. черт.3)
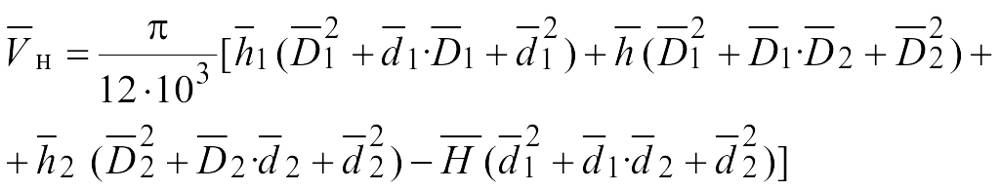
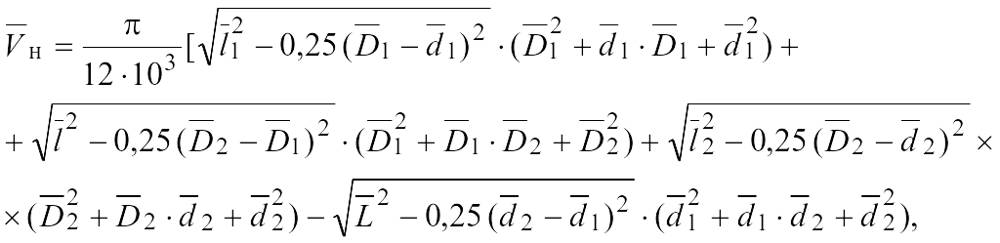
где — средняя высота верхнего конуса бобины, мм;
— средняя высота среднего конуса бобины, мм;
— средняя высота нижнего конуса бобины, мм;
— средний диаметр патрона у верхнего основания верхнего конуса бобины, мм;
— средний диаметр патрона у нижнего основания конуса бобины, мм;
— средний диаметр верхнего основания среднего конуса бобины, мм;
— средний диаметр нижнего основания среднего конуса бобины, мм;
— средняя образующая верхнего конуса бобины, мм;
— средняя образующая нижнего конуса бобины, мм;
— средняя образующая среднего конуса бобины, мм;
— средняя образующая патрона, занятого нитью, мм;
в биноконусных бобинах (см. черт.4)
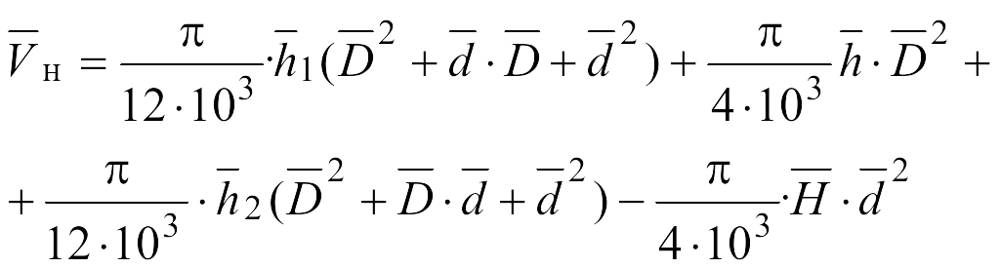
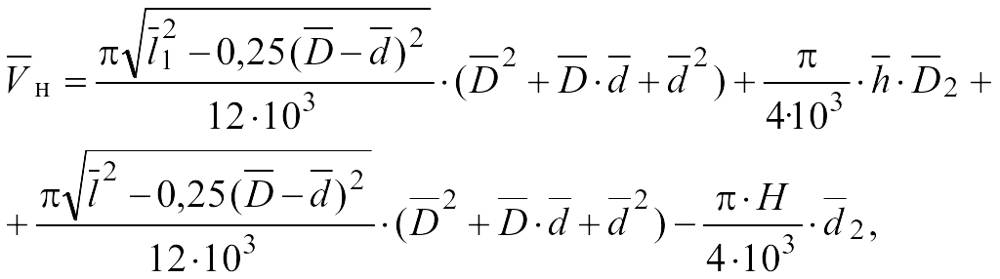
где — средний диаметр патрона, мм;
— средний диаметр бобины, мм.
5.1.-5.1.2. (Измененная редакция, Изм. N 2).
5.2. (Исключен, Изм. N 3).
Разделы 6 и 7 (Исключены, Изм. N 2).
Приложения 1-8 (Исключены, Изм. N 2).
Приложение 9 (Исключено, Изм. N 3).
Электронный текст документа
и сверен по:
М.: Издательство стандартов, 1996
Содержание книги
Предыдующая страница
§16. Превращение энергии в электрических и магнитных явлениях
16.9 Превращения энергии при изменении индуктивности цепи.
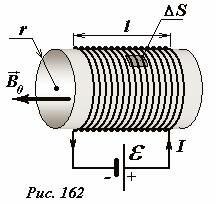
Энергия магнитного поля соленоида зависит от индуктивности последнего. Поэтому при изменении размеров соленоида или изменении материала сердечника в цепи происходят процессы, приводящие к изменению энергии магнитного поля. Для поддержания постоянного электрического тока в цепи, содержащей соленоид, присутствие источника ЭДС обязательно (Рис. 162). Следовательно, нам необходимо принимать во внимание не только изменения магнитного поля соленоида, но и процессы, протекающие на других участках цепи, в том числе и источнике.
Рассмотрим подробно превращения энергии при изменении радиуса соленоида. Для наглядности можно считать, что обмотка соленоида изготовлена из упругой проволоки, способной растягиваться. Прежде всего, обратим внимание, что на обмотку соленоида действуют силы со стороны магнитного поля, создаваемого электрическим током в самой обмотке.
Найдем силы, действующие на обмотку длинного соленоида с плотной намоткой, для которого можно пренебречь краевыми эффектами. Магнитное поле внутри такого соленоида является однородным, вектор индукции направлен вдоль оси соленоида, а его модуль равен
(~B_0 = mu_0 nI) , (1)
где (~n = frac{N}{l}) — плотность намотки, равная числу витков на единицу длины соленоида, I — сила тока в обмотке. Вне соленоида магнитное поле отсутствует.
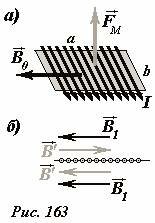
Выделим на поверхности соленоида малую площадку площадью (Delta S = ab) (Рис. 163а). Сила Ампера, действующие на участки витков обмотки, находящиеся на выделенной площадке, направлена перпендикулярно направлению тока и вектору индукции поля. Модуль этой силы рассчитывается по формуле
(~F = I N_1 B_1 b) , (2)
где (N_1 = na) — число витков, лежащих на площадке, B1 — индукция магнитного поля, создаваемого всеми элементами соленоида, кроме лежащих на площадке.
Вспомните расчет силы, действующей на заряженную пластину конденсатора со стороны электрического поля. При выводе формулы для этой силы мы также учитывали напряженность поля, создаваемого всеми зарядами, кроме находящихся на площадке. Мы показали, что напряженность этого поля в два раза меньше напряженности суммарного поля.
Чтобы определить требуемую индукцию поля, представим суммарное поле в виде суммы полей[~vec B’] — создаваемого током площадки и (~vec B_1) — создаваемого всеми остальными участками обмотки (Рис. 163б). Внутри соленоида эти векторы направлены одинаково и их сумма равна индукции суммарного поля (B’ + B_1 = B_0). Вне соленоида эти векторы направлены противоположно и их сумма равна нулю (B’ — B_1 = 0). Из этих соотношений следует, что индукция поля, действующего на выделенную площадку, в два раза меньше индукции суммарного поля внутри соленоида (~B_1 = frac{B_0}{2}). Таким образом, на выделенную площадку действует сила, которая рассчитывается по формулам
(~F = I N_1 B_1 b = I n frac{B_0}{2} ab = frac{mu_0 n^2 I^2}{2} ab = frac{(mu_0 n I)^2}{2 mu_0} ab = frac{B^2_0}{2 mu_0} ab) . (3)
Найденная сила пропорциональна площади выделенной площадки и направлена перпендикулярно ей, поэтому можно говорить о давлении магнитного поля на поверхность соленоида. Существенно, что величина этого давления равна плотности энергии магнитного поля вблизи площадки
(~p = frac{F}{Delta S} = frac{B^2_0}{2 mu_0} = w_M) . (4)
аналогично тому, что давление электрического поля на поверхность проводника со стороны электрического поля равно плотности энергии этого поля.
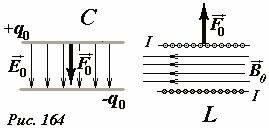
Продолжим сравнение действия электрического поля в конденсаторе и магнитного поля в соленоиде. Самое существенное отличие заключается в направлении действия силы (Рис. 164). На обкладки конденсатора действует сила, направленная внутрь, в сторону части пространства, занятого полем. Если предоставить пластинам возможность двигаться, то сила их взаимодействия приведет к уменьшению расстояния между пластинами, уменьшению объема, занятого полем, уменьшению суммарной энергии поля (при неизменном заряде на пластКурсивное начертаниеинах). При этом энергия электрического поля переходит в кинетическую энергию движущихся пластин.
На обмотку соленоида со стороны магнитного поля действует сила, направленная наружу, в сторону противоположную части пространства, занятого полем. Если обмотка соленоида способна расширятся, то силы взаимодействия приведут к увеличению радиуса обмотки, увеличению объема, занятого полем, увеличению его суммарной энергии (при неизменной силе тока в обмотке). Таким образом, мы приходим к парадоксальному выводу: магнитное поле совершает работу и при этом его энергия увеличивается – отсюда уже недалеко до «вечного двигателя»! Не стоит обольщаться этим «гениальным изобретением», достаточно вспомнить, что для поддержания тока в цепи, в ней должен быть источник, обладающий энергией и отдающий ее в цепь. Кроме того, при движении зараженной пластины в электрическом поле распределение зарядов и их величина могут оставаться неизменными. При движении проводника в магнитном поле распределение электрических токов и их величина изменяются вследствие явления электромагнитной индукции.
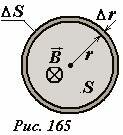
Рассмотрим, какие изменения произойдут в рассматриваемой системе, показанной на рис. 162, при увеличении радиуса обмотки на малую величину Δr (то есть при увеличении площади сечения на величину ΔS — Рис. 165). Изменение силы тока в цепи описывается уравнением закона Ома для полной цепи
(~varepsilon + varepsilon_{ind} = IR) , (5)
где R — полное сопротивление цепи, εind — ЭДС индукции, возникающей в соленоиде, которая определяется законом Фарадея
(~varepsilon_{ind} = -frac{Delta Phi}{Delta t}) , (6)
где (~Phi = NSB = nlS (mu_0 n I) = mu_0 n^2 lSI) — магнитный поток через все N витков катушки (l — длина обмотки). На основании этих законов запишем уравнение
(~varepsilon = IR + frac{Delta Phi}{Delta t}) ,
которое, как обычно, умножим на малую величину заряда Δq, протекающего по цепи за малый промежуток времени Δt, в результате получим соотношение
(~varepsilon Delta q = IR Delta q + frac{Delta Phi}{Delta t} Delta q = IR Delta q + I Delta Phi) . (7)
В данном случае поток через соленоид может изменяться по двум причинам – изменения силы тока и изменения площади поперечного сечения соленоида. Пусть в некоторый момент времени сила тока в обмотке равнялась I, а площадь сечения S, затем за малый промежуток времени Δt сила тока изменилась на ΔI, а площадь — на ΔS. Тогда изменения магнитного потока можно представить в виде
(~Delta Phi = mu_0 n^2 l Delta(IS) = mu_0 n^2 l ((I + Delta I)(S + Delta S) — IS) = mu_0 n^2 l (S Delta I + IDelta S)) ,
на последнем шаге преобразований мы пренебрегли произведением малых величин ΔIΔS. Подставим полученное выражение в уравнение (7)
(~varepsilon Delta q = IR Delta q + I Delta Phi = IR Delta q + I mu_0 n^2 l (S Delta I + IDelta S) = IR Delta q + mu_0 n^2 l S I Delta I + mu_0 n^2 I^2 l Delta S) . (8)
Выясним теперь смысл каждого члена этого уравнения, тем более, что некоторые из них уже встречались нам ранее: [varepsilon Delta q] — работа источника ЭДС по перемещению заряда Δq; [~IR Delta q = I^2 R Delta t] — количество теплоты, выделившееся в цепи при прохождении заряда Δq; [~mu_0 n^2 l S I Delta I = mu_0 n^2 Delta left( frac{I^2}{2}right) Sl = Delta left( frac{mu_0 n^2 I^2}{2}right) Sl = Delta left( frac{B^2}{2mu_0}right) Sl] — (здесь (B = mu_0 n I) — индукция магнитного поля внутри соленоида) изменение энергии магнитного поля вследствие изменения силы тока в соленоиде (изменение энергии поля в первоначальном объеме соленоида);
- наконец, последнее слагаемое преобразуется к виду (~mu_0 n^2 I^2 l Delta S = 2 left( frac{B^2}{2mu_0}right) Delta V) и равно удвоенной (!?) энергии магнитного поля в части приращенного объема соленоида ΔV. Смысл половины этого слагаемого, то есть (~left( frac{B^2}{2mu_0}right) Delta V) , понятен – это увеличение энергии поля вследствие увеличения его объема, осталось найти смысл оставшейся величины (~left( frac{B^2}{2mu_0}right) Delta V) . Мы не случайно начали рассуждения данного раздела рассмотрения сил, действующих на обмотку – эти силы увеличивают размер соленоида, следовательно, совершают работу. В результате совершения этой работы увеличивается механическая энергия обмотки – если она упругая и деформируемая, то увеличивается энергия ее упругой деформации, возможно, что часть этой энергии идет на увеличение кинетической энергии расширяющихся витков. Выяснение этих деталей требует более конкретного описания механических свойств обмотки. Не будем их конкретизировать, покажем, что оставшееся слагаемое действительно равно работе сил поля над расширяющейся обмоткой. Еще раз взглянем на выделенную на боковой поверхности соленоида площадку (Рис. 162, 163) со сторонами a и b, на нее действует сила pab (p — давление поля). При смещении этой площадки на расстояние Δr в направлении действия силы, магнитное поле совершает работу (~delta A = F Delta r = pab Delta r = p Delta V_{ab}) , где (Delta V_{ab}) — изменение объема соленоида при смещении рассматриваемой площадки. Так как давление на все точки поверхности соленоида одинаково, то суммарная работа поля по смещению всех участков его поверхности будет равна (A = p Delta V) , где ΔV — полное изменение объема соленоида. Используя формулу (4) для давления магнитного поля, получим, что работа по расширению соленоида равна
(~A = left( frac{B^2}{2mu_0}right) Delta V) .
Таким образом, энергетический баланс и в этом случае сходится: работа, совершенная источником ЭДС по перемещению заряда (varepsilon Delta q), расходуется на:
- — преодоление сил сопротивления (в результате чего выделяется теплота (delta Q = IR Delta q));
- — увеличение энергии поля, как вследствие изменения его индукции (и плотности энергии) (~Delta W_B = Delta left( frac{B^2}{2mu_0}right) V) , так и вследствие изменения объема, занятого полем (~Delta W_V = left( frac{B^2}{2mu_0}right) Delta V);
- — увеличение механической энергии обмотки, которая возрастает благодаря работе поля (~Delta W_{obm} = A = left( frac{B^2}{2mu_0}right) Delta V).
Следующая страница