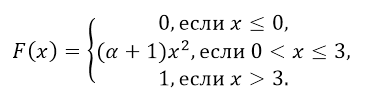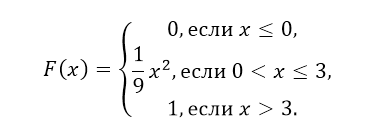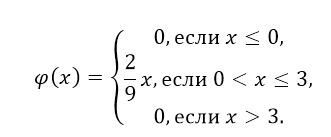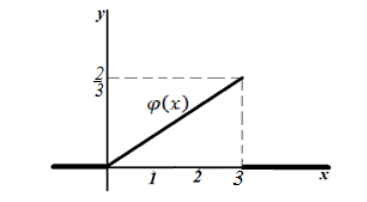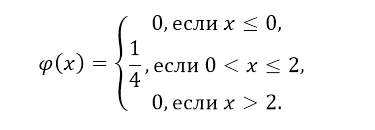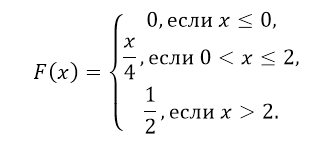Как найти плотность распределения статистика - Исправление недочетов и поиск решений вместе с Examum.ru

Вопрос 11. Плотность
распределения (абсолютная и относительная).

Группировка — это расчленение
изучаемой статистической совокупности
на части по одному или нескольким
группировочным признакам. Правильно
проведенная группировка в значительной
мере обеспечивает достоверность всего
статистического исследования.

Вариация
— различие значений
признака у разных единиц одновременно
существующей совокупности.

Частоты – f – это
численности отдельных вариаций или
каждой группы вариационного ряда. Сумма
всех частот называется объемом
совокупности и определяет число элементов
всей совокупности.

Показатель численности групп представлен
либо частотой (абсолютные числа), либо
частостью (удельным весом каждой группы
— относительные), либо как те и другие
совместно (в двух параллельных столбцах).

Частость — относительное выражение
частоты, представляет собой отношение
частоты к сумме частот.

Вариационные ряды — ряды
распределения, построенные по
количественному признаку,
определение интервала группировки
должно соответствовать переходу от
одного качества к другому.

Если приходится иметь дело с вариационным
рядом с неравными интервалами, то для
сопоставимости нужно частоты или
частости привести к единице интервала.
Полученное отношение называется
плотностью распределения:

Отношения частот или частостей к
величинам интервала называются плотностью
распределения.

Абсолютной плотностью распределения

называется число, показывающее, сколько
единиц совокупности приходится на
единицу размера интервала в отдельных
группах ряда

Относительная плотность распределения

определяется как частное от деления
частности W отдельной группы ряда на
единицу размера интервала

Абсолютная плотность распределения	Относительная плотность распределение

Плотность распределения используется
как для расчета обобщающих показателей,
так и для графического изображения
вариационных рядов с неравными
интервалами.

Огива и кумулята
распределения по урожайности

Источник

Определение плотности распределения

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Как нам уже известно, случайную величину можно задавать с помощью таблицы или с помощью функции распределения вероятности. Предположим теперь, что случайная величина $X$ является непрерывной, а функция распределения вероятности $F(x)$ непрерывна и дифференцируема в своей области определения. Тогда для такой случайной величины существует еще один способ её задания — задания с помощью плотности распределения.

Определение 1

Плотностью распределения $varphi (x)$ непрерыной случайной величины называется первая производная от функции распределения вероятности $F(x)$.

Примечание 1

!!! Подчеркнем, что данное понятие не применимо к дискретной случайной величине.

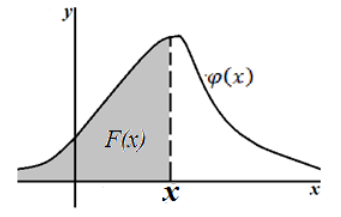
Геометрически, плотность распределения связана с функцией распределения вероятностей следующим образом: площадь криволинейной трапеции, ограниченной графиком плотности распределения и находящейся по левую сторону от величины $x$ и есть функция распределения вероятности (рис. 1).

Рисунок 1. Связь функций $varphi (x)$ и $F(x)$.

То есть:

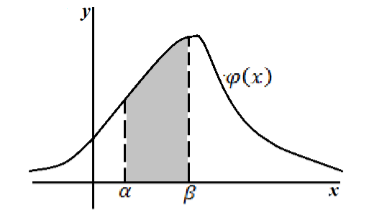
Геометрический смысл: вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной графиком функции распределения $varphi left(xright)$ и прямыми $x=alpha ,$ $x=beta $ и $y=0$ (рис. 2).

Рисунок 2. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.

«Определение плотности распределения» 👇

Примеры задач на понятие плотности распределения

Пример 1

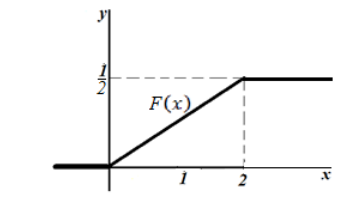
Пусть функция распределения $F(x)$ случайной величины $X$ имеет следующий вид:

Рисунок 3.

а) Найти значение $alpha $.

б) Найти плотность распределения $varphi left(xright)$.

в) Построить график плотности распределения.

г) Найти вероятность попадания случайной величины в интервал $left(1,2right)$

Решение:

а) Так как необходимо найти плотность распределения, то случайная величина $X$ является непрерывной.

Тогда, при $x=3$, получим, что $(alpha +1)x^2=1$, то есть

[9alpha +9=1,] [9alpha =-8,] [alpha =-frac{8}{9}.]

То есть:

Рисунок 4.

б) Так как $varphi (x)$ = $F'(x)$, то получим:

Рисунок 5.

в) Построим график функции $varphi left(xright)$.

Рисунок 6.

г) Воспользовавшись геометрическим смыслом функции плотности распределения получим, что нам нужно найти площадь криволинейной трапеции, ограниченной функцией $y=frac{2}{9}x$ и прямыми $x=1,$ $x=2$ и $y=0$.

Таким образом, получим:

[Pleft(1

Пример 2

Найти функцию распределения непрерывной случайной величины и построить её график, если плотность распределения имеет вид:

Рисунок 7.

Решение.

При решении будем использовать следующую формулу: $Fleft(xright)=intlimits^x_{-infty }{varphi (x)dx}$

begin{enumerate}
item При $xle 0$, по формуле, получим:

[Fleft(xright)=intlimits^x_{-infty }{varphi (x)dx}=intlimits^x_{-infty }{0dx}=0]

item При $0
[Fleft(xright)=intlimits^x_{-infty }{varphi (x)}=intlimits^0_{-infty }{0dx}+intlimits^x_0{frac{dx}{4}}=0+frac{x}{4}-0=frac{x}{4}]

item При $x>2$, по формуле, получим:

[Fleft(xright)=intlimits^x_{-infty }{varphi (x)}=intlimits^0_{-infty }{0dx}+intlimits^2_0{frac{dx}{4}}+intlimits^x_2{0dx}=0+frac{1}{2}-0+0=frac{1}{2}]

end{enumerate}

Таким образом, функция распределения имеет вид:

Рисунок 8.

Построим её график.

Рисунок 9.

Примечание 2

!!! Заметим, что, так как дана плотность распределения, то случайная величина является непрерывной. Следовательно, функция $F(x)$ также должна быть непрерывной (как и получилось в нашем примере). Это может служить косвенной проверкой правильности решения такого рода задач.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 20.02.2023

Источник

Как найти плотность распределения

Плотность распределения удобна тем, что с ее помощью окрестность больших (меньших) значений случайной величины СВ легко представить в графической форме. С общетеоретической точки зрения ее легко найти, исходя из определения. Поэтому имеет смысл сосредоточиться на построении плотности вероятности исходя из данных наблюдений, то есть с помощью методов математической статистики.

Инструкция

Начните работу с построения таблицы статистического ряда. Здесь придерживаются следующего порядка действий: 1. Весь диапазон значений имеющихся опытных данных (статистической совокупности, выборки) разбейте на интервалы (разряды), которых не должно быть как слишком много, так и слишком мало (в каждом должно произойти достаточное усреднение). В таблице укажите границы этих разрядов.2. Подсчитайте число наблюдений, приходящихся на каждый разряд (при попадании значения на границу разряда можно добавить 1 как к левому, так и к правому разряду или по 0,5 для каждого).3. Вычислите частоты разрядов в соответствии с p*i= ni/n, где n – общее число наблюдений, а ni – число наблюдений, приходящихся на i-й разряд

Графическое изображение статистического ряда называется гистограммой. Порядок ее построения состоит в том, что на оси абсцисс откладываются разряды и на них (как на основаниях) строятся прямоугольники, площади которых равны частотам данных разрядов. Очевидно, что высоты этих прямоугольников равны относительным плотностям, также внесенным в таблицу статистического ряда. Рассмотрите статистический ряд, составленный из n=100 ошибок измерения дальности с помощью дальномера (см. рис. 1).

Для данного примера гистограмма имеет вид (рис. 2).

Сумма частот всех разрядов очевидно равна единице. Поэтому и площадь под гистограммой – единица, что является аналогом условия нормировки плотности вероятности. Таким образом, если через верхние основания прямоугольников гистограммы провести непрерывную кривую («округлить» гистограмму), то она, в первом приближении, и будет предполагаемой плотностью вероятности наблюдаемой случайной величины. По виду этой кривой можно сделать предположение о законе распределения. В данном примере следует остановиться на распределении Гаусса.

Для завершения процесса работы, необходимо оценить параметры распределения. Так, для гауссовского распределения — это математическое ожидание и дисперсия. Их оценки на основе статистического ряда вычисляются следующим образом: пусть число выбранных разрядов (интервалов) r, а середины интервалов лежат в точках ai. Тогда (см. рис. 3).На рисунке 3 приведена и аналитическая запись искомой плотности вероятности (плотности распределения).

Источники:

Тихонов В.И. Статистическая радиотехника. – М.: Радио и связь, 1982. – 624 с.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

— функцию
распределения вероятностей;

—
математическое ожидание;

—
дисперсию;

— среднее
квадратическое отклонение;

— вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

—
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

—
составить функцию плотности распределения и построить ее график;

— найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

— найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник