Как найти плотность треугольник

Плотность вещества

О чем эта статья:

Масса

Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.

До недавнего времени в Международном бюро мер и весов в Париже хранился цилиндр массой один килограмм. Цилиндр был изготовлен из сплава иридия и платины и служил для всего мира эталоном килограмма. Правда, со временем его масса изменилась, и пришлось придумать новый эталон — электромагнитные весы.

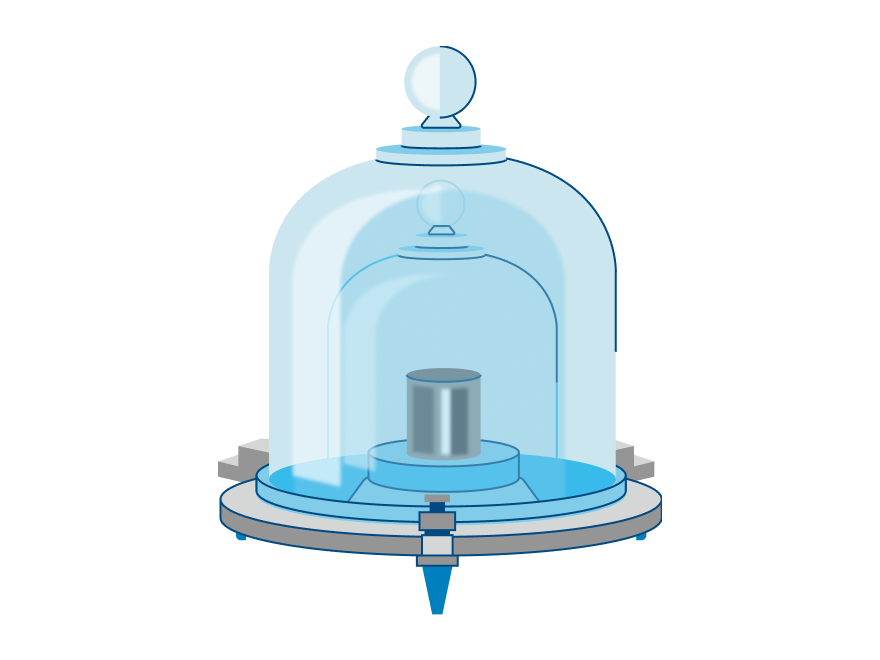
Высота этого цилиндра была приблизительно равна 4 см, но чтобы его поднять, нужно было приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.

Второй закон Ньютона

F = ma

a — ускорение [м/с 2 ]

В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6,67 · 10 −11 м 3 · кг −1 · с −2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне. 🙃

Откуда берется масса

Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.

Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.

Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

Скажем, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

Формула объема параллелепипеда

V = abc

А для цилиндра будет справедлива такая формула:

Формула объема цилиндра

V = Sh

S — площадь основания [м 2 ]

Плотность вещества

Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объему.

Формула плотности вещества

р — плотность вещества [кг/м 3 ]

m — масса вещества [кг]

V — объем вещества [м 3 ]

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Площадь равнобедренного треугольника — формулы вычисления

Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.

Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.

Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;

через угол между двумя сторонами и величину одной из них;

по двум сторонам;

через синус противолежащего основанию угла;

зная синус прилежащего угла и др.

Площадь равнобедренного треугольника через высоту

Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.

У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.

И общая их площадь сводится к:

b — размер основания;

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.

Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

Площадь равнобедренного треугольника через синус угла

В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.

В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Формула площади равнобедренного треугольника через тангенс угла

Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.

Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90 0 — угол OPQ.

SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2

Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.

Here is the simple online DMV (i.e) Density Mass Volume Magic Triangle Calculator to calculate the volume of an object using magic triangle method. The DMV triangle tells the relationship between density, mass and volume of the triangle. Mass (Kg) is a measure of the amount of matter in an object, while density (Kg/m₃) is the amount of mass per unit volume of the object. This Density Mass Volume Calculator works based on the DMV Triangle formula, Volume = Mass / Density.

Here is the simple online DMV (i.e) Density Mass Volume Magic Triangle Calculator to calculate the volume of an object using magic triangle method. The DMV triangle tells the relationship between density, mass and volume of the triangle. Mass (Kg) is a measure of the amount of matter in an object, while density (Kg/m₃) is the amount of mass per unit volume of the object. This Density Mass Volume Calculator works based on the DMV Triangle formula, Volume = Mass / Density.

Узнайте, как рассчитать плотность, массу или объем твердого объекта с помощью этого удобного визуального инструмента.

Canva

Что такое плотность?

Плотность — это мера того, насколько компактный (плотный) объект. Если объект имеет большую плотность, чем вода, объект утонет в воде. Если он имеет меньшую плотность, чем вода, он будет плавать.

Как определить плотность твердого объекта

Чтобы рассчитать плотность объекта, нам нужно знать массу и объем объекта. Затем мы можем подставить эти значения в следующее уравнение для расчета плотности объекта:

Эта формула часто записывается с использованием следующих символов:

• ρ : плотность
• m: масса
• V: объем

Используя эти символы в качестве переменных, наша формула теперь выглядит так:

Треугольник масса-плотность-объем помогает нам визуализировать отношения между этими тремя переменными.

Canva

Что такое треугольник плотность-масса-объем?

Треугольник плотность-масса-объем (изображенный выше) — это визуальный инструмент, который мы можем использовать, чтобы выяснить, как вычислить плотность, массу или объем твердого объекта, если нам известны два оставшихся значения. Треугольник разделен на три части: плотность занимает верхнюю часть, а масса и объем — две нижние части.

Положение каждого элемента треугольника показывает нам, как они соотносятся друг с другом через формулу выше ( плотность = масса / объем или ρ = м / об ).

Как рассчитать плотность

Если мы хотим вычислить плотность, мы просто скрываем плотность в треугольнике и смотрим, что остается. Поскольку масса выше объема, мы делим массу на объем, чтобы получить плотность.

Как рассчитать массу

Если мы хотим вычислить массу, мы просто скрываем массу в треугольнике и смотрим, что остается. Поскольку плотность и объем находятся рядом, мы умножаем плотность на объем, чтобы получить массу.

Как рассчитать объем

Если мы хотим рассчитать объем, мы просто закрываем объем в треугольнике и смотрим, что остается. Поскольку масса выше плотности, мы делим массу на плотность, чтобы получить объем.

Примеры проблем с процессами и решениями

Давайте рассмотрим несколько примеров проблем и решим их, используя треугольник плотность-масса-объем, описанный выше.

В этом первом примере нам нужно вычислить плотность этой прямоугольной призмы или кубоида.

Пример 1

Сплошная прямоугольная коробка имеет длину 6 см , ширину 4 см и высоту 5 см . Позанимайтесь плотность коробки, если масса коробки 200 г .

Этот вопрос просит нас определить плотность. Следовательно, нам понадобится формула для плотности (Density = Mass / Volume) .

Однако в вопросе указывается масса коробки, но не указывается объем, поэтому нам нужно определить объем коробки, прежде чем мы сможем вычислить плотность.

Поскольку коробка имеет форму куба, объем можно определить, умножив длины трех сторон вместе:

Теперь, когда у нас есть объем, можно рассчитать плотность:

Во втором примере нам нужно вычислить массу треугольной призмы.

Пример 2

Определите массу этой треугольной призмы, если плотность равна 3 г / см³ .

На этот раз нас просят вычислить массу, поэтому нам понадобится формула для массы (Масса = Плотность * Объем) .

В этом вопросе нам дается плотность, но не объем, поэтому давайте начнем с вычисления объема треугольной призмы. Площадь поперечного сечения призмы можно найти по формуле Площадь = ½ * (Основание * Высота) .

Теперь объем призмы можно найти, умножив эту площадь на длину:

Теперь, когда у нас есть объем, мы можем вычислить массу треугольной призмы:

Вопросы и Ответы

Вопрос: Емкость — это прямоугольная призма. Его размеры 50 см X 40 см X 10 см. Если он наполнен водой, какова масса воды?

Ответ: Сначала определите объем прямоугольной призмы, умножив три измерения вместе: 50, умноженное на 40, умноженное на 10, получится 20 000 см ^ 3. Теперь, поскольку 1 см ^ 3 — это то же самое, что 1 г воды, ответ — 20 000 г (или 20 кг).

Вопрос: Сколько массы в прямоугольной призме высотой 100, длиной 25 и шириной 3?

Ответ: Сначала найдите объем, умножив числа, чтобы получить 7500. Теперь умножьте этот ответ на плотность прямоугольной призмы, чтобы получить массу.

Вопрос: Как рассчитать плотность куба?

Ответ: Сначала определите объем куба, отсчитав длину стороны куба.

Затем разделите массу (указанную в вопросе) на объем.

Вопрос: Что такое плотность?

Ответ: Плотность можно вычислить, разделив массу на объем.

Вопрос: Деревянный блок — это прямоугольная призма. Его длина — 8 см, длина одной из двух сторон идеального квадрата — 2 см, масса деревянного блока на электронных весах составляет 150 граммов, какова плотность деревянного блока?

Ответ: Сначала определите объем блока 32 см ^ 3 (8 раз по 2 раза по 2).

Затем разделите 150 на 32, чтобы получить 4,6875 г / см ^ 3.

На этой странице находится вопрос Использую»волшебный треугольник» , напишите формулы для расчета : плотность — ?. Здесь же – ответы на него,
и похожие вопросы в категории Физика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Треугольник Шварца — сферический треугольник, который можно использовать для создания мозаики на сфере, возможно с наложением, путём отражений треугольника относительно сторон. Треугольники классифицированы в работе немецкого математика Карла Шварца 1873 года^[1].

Треугольники Шварца можно определить в более общем виде как мозаики на сфере, евклидовой или гиперболической плоскости. Каждый треугольник Шварца на сфере определяет конечную группу, в то время как на евклидовой плоскости они определяют бесконечные группы.

Треугольник Шварца представляется тремя рациональными числами (p q r), каждое из которых задаёт угол в вершине. Значение n/d означает, что угол в вершине треугольника равен d/n развёрнутого угла. 2 означает прямоугольный треугольник. Если эти числа целые, треугольник называется треугольником Мёбиуса и он соответствует мозаике без перекрытий, а группа симметрии называется группой треугольника. На сфере имеется 3 треугольника Мёбиуса и ещё одно однопараметрическое семейство. На плоскости имеется три треугольника Мёбиуса, а в гиперболическом пространстве имеется семейство треугольников Мёбиуса с тремя параметрами и нет исключительных объектов^[en].

Пространство решенийПравить

Фундаментальная область в виде треугольника (p q r) может существовать в различных пространствах в зависимости от суммы обратных величин этих целых:

  Сфера

  Евклидова плоскость

  Гиперболическая плоскость

Проще говоря, сумма углов треугольника в евклидовой плоскости равна π, в то время как на сфере сумма углов больше π, а на гиперболической плоскости сумма меньше π.

Графическое представлениеПравить

Треугольник Шварца представляется графически как треугольный граф. Каждая вершина соответствует стороне (зеркалу) треугольника Шварца. Каждое ребро помечено рациональным значением, соответствующим порядку отражения, которое равно π/внешний угол.

Schwarz triangle (p q r) on sphere

Schwarz triangle graph

Рёбра с порядком 2 представляют перпендикулярные зеркала, которые в этой диаграмме можно опускать. Диаграмма Коксетера — Дынкина представляет эти треугольные графы без рёбер порядка 2.

Можно использовать группу Коксетера для более простой записи, как (p q r) для циклических графов, (p q 2) = [p,q] для прямоугольных треугольников) и (p 2 2) = [p]×[].

Список треугольников ШварцаПравить

Треугольники Мёбиуса на сфереПравить

(2 2 2) или [2,2]	(3 2 2) или [3,2]	…
(3 3 2) или [3,3]	(4 3 2) или [4,3]	(5 3 2) или [5,3]

Треугольники Шварца с целыми числами, также называемые треугольниками Мёбиуса, включают однопараметрическое семейство и три исключительных^[en] случая:

1. [p,2] или (p 2 2) – диэдральная симметрия,      
2. [3,3] или (3 3 2) – Тетраэдральная симметрия,      
3. [4,3] или (4 3 2) – Октаэдральная симметрия^[en],      
4. [5,3] или (5 3 2) – Икосаэдральная симметрия,      

Треугольники Шварца на сфере, сгруппированные по плотностиПравить

Треугольники Шварца (p q r), сгруппированные по плотности^[en]:

Плотность	треугольник Шварца
1	(2 3 3), (2 3 4), (2 3 5), (2 2 n)
d	(2 2 n/d)
2	(3/2 3 3), (3/2 4 4), (3/2 5 5), (5/2 3 3)
3	(2 3/2 3), (2 5/2 5)
4	(3 4/3 4), (3 5/3 5)
5	(2 3/2 3/2), (2 3/2 4)
6	(3/2 3/2 3/2), (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7	(2 3 4/3), (2 3 5/2)
8	(3/2 5/2 5)
9	(2 5/3 5)
10	(3 5/3 5/2), (3 5/4 5)
11	(2 3/2 4/3), (2 3/2 5)
13	(2 3 5/3)
14	(3/2 4/3 4/3), (3/2 5/2 5/2), (3 3 5/4)
16	(3 5/4 5/2)
17	(2 3/2 5/2)
18	(3/2 3 5/3), (5/3 5/3 5/2)
19	(2 3 5/4)
21	(2 5/4 5/2)
22	(3/2 3/2 5/2)
23	(2 3/2 5/3)
26	(3/2 5/3 5/3)
27	(2 5/4 5/3)
29	(2 3/2 5/4)
32	(3/2 5/45/3)
34	(3/2 3/2 5/4)
38	(3/2 5/4 5/4)
42	(5/4 5/4 5/4)

Треугольники на евклидовой плоскостиПравить

Плотность 1:

1. (3 3 3) – 60-60-60 (равносторонний)
2. (4 4 2) – 45-45-90^[en] (равнобедренный прямоугольный)
3. (6 3 2) – 30-60-90^[en]
4. (2 2 ∞) — 90-90-0 «треугольник»

Плотность 2:

1. (6 6 3/2) — 120-30-30 треугольник

Плотность ∞:

1. (4 4/3 ∞)
2. (3 3/2 ∞)
3. (6 6/5 ∞)

Треугольники на гиперболической плоскостиПравить

(7 3 2)	(8 3 2)	(5 4 2)
(4 3 3)	(4 4 3)	(∞ ∞ ∞)
Фундаментальные области треугольников (p q r)

Плотность 1:

• (2 3 7), (2 3 8), (2 3 9) … (2 3 ∞)
• (2 4 5), (2 4 6), (2 4 7) … (2 4 ∞)
• (2 5 5), (2 5 6), (2 5 7) … (2 5 ∞)
• (2 6 6), (2 6 7), (2 6 … (2 6 ∞)
• (3 3 4), (3 3 5), (3 3 6) … (3 3 ∞)
• (3 4 4), (3 4 5), (3 4 6) … (3 4 ∞)
• (3 5 5), (3 5 6), (3 5 7) … (3 5 ∞)
• (3 6 6), (3 6 7), (3 6 … (3 6 ∞)
• …
• (∞ ∞ ∞)

Плотность 2:

• (3/2 7 7), (3/2 8 8), (3/2 9 9) … (3/2 ∞ ∞)
• (5/2 4 4), (5/2 5 5), (5/2 6 6) … (5/2 ∞ ∞)
• (7/2 3 3), (7/2 4 4), (7/2 5 5) … (7/2 ∞ ∞)
• (9/2 3 3), (9/2 4 4), (9/2 5 5) … (9/2 ∞ ∞)
• …

Плотность 3:

• (2 7/2 7), (2 9/2 9), (2 11/2 11) …

Плотность 4:

• (7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11) …

Плотность 6:

• (7/4 7 7), (9/4 9 9), (11/4 11 11) …

Плотность 10:

• (3 7/2 7)

Треугольник Шварца (2 3 7) является наименьшим гиперболическим треугольником Шварца и представляет особый интерес. Его группа треугольника (или, более точно, группа фон Дика сохраняющих ориентацию изометрий с индексом 2) является группой треугольников (2,3,7)^[en], которая является универсальной группой для всех групп Гурвица^[en] — максимальных групп изометрий римановых поверхностей. Все группы Гурвица являются факторгруппами группы треугольников (2,3,7) и все поверхности Гурвица покрываются мозаиками из треугольников Шварца (2,3,7). Наименьшая группа Гурвица — это простая группа порядка 168, вторая наименьшая неабелева простая группа, которая изоморфна PSL(2,7) и ассоциирована с поверхностью Гурвица рода 3, — это квартика Клейна^[en].

Треугольник (2 3 замощает поверхность Больца, высокосимметричную (но не являющуюся поверхностью Гурвица) поверхность рода 2.

Треугольники с одним нецелым углом, перечисленные выше, впервые классифицированы Антони В. Кнаппом (англ. Anthony W. Knapp) в статье 1968 года^[2]. Список треугольников с несколькими нецелыми углами даны в статье Клименко и Сакума 1998 года^[3].

См. такжеПравить

• Список однородных многогранников по порождающим треугольникам Шварца
• Символ Витхоффа^[en]
• Построение Витхоффа
• Однородный многогранник
• Невыпуклый однородный многогранник^[en]
• Плотность политопа^[en]
• Тетраэдр Гурса
• Правильные однородные мозаики^[en]
• Однородные мозаики на гиперболической плоскости

ПримечанияПравить

ЛитератураПравить

СсылкиПравить

• Weisstein, Eric W. Schwarz triangle (англ.) на сайте Wolfram MathWorld.
• KlitzingPolytopes The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra