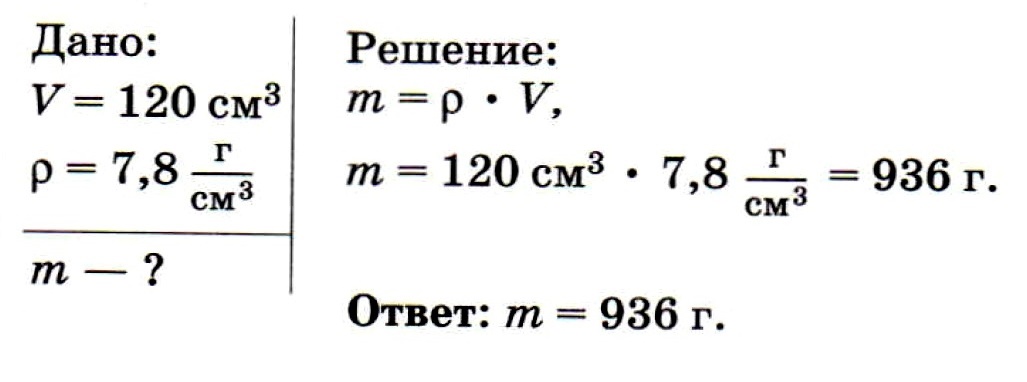Как найти плотность в математике 7 класс

Задачи на плотность, массу и объем с решением

Формулы, используемые по теме «Задачи на плотность, массу и объем с решением»

Название величины	Обозначение	Единицы измерения	Формула
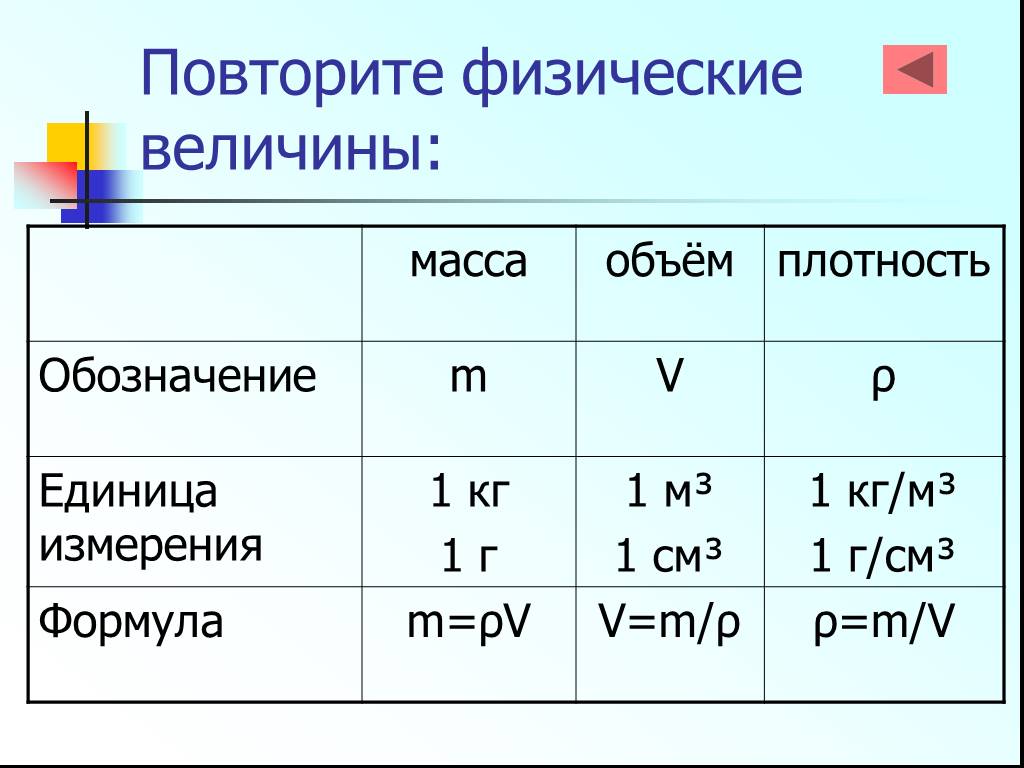
Масса	m	кг	m = ρ * V
Объем	V	м3	V = m / ρ
Плотность	ρ	г/см3, кг/м3	ρ = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Найдите плотность молока, если 206 г молока занимают объем 200 см³?

---

Задача № 2.
 Определите объем кирпича, если его масса 5 кг?

---

Задача № 3.
 Определите массу стальной детали объёмом 120 см³

---

Задача № 4.
 Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м³) меньше плотности стали (ρ₁ = 7800 кг/м³). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

---

Задача № 5.
 Определите плотность мела, если масса его куска объемом 20 см³ равна 48 г. Выразите эту плотность в кг/м³ и в г/см³.

Ответ: Плотность мела 2,4 г/см³, или 2400 кг/м³.

---

Задача № 6.
 Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

ОТВЕТ: 160 кг.

Указания к решению. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м³ • 0,04 м² • 5 м = 160 кг.

---

Задача № 7.
 Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

---

Задача № 8 (повышенной сложности).
 Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

---

Задача № 9 (олимпиадный уровень).
 Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м³

Задачи на плотность,
массу и объем с решением

---

Справочный материал для
«Задачи на плотность, массу и объем«

Таблица плотности веществ.

Как, зная только массу, рассчитать плотность?

1. Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
2. Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
3. Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
4. Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
5. Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
6. Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
7. Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

---

Задачи на плотность,
массу и объем с решением

ВОПРОСЫ ОТ ПОЛЬЗОВАТЕЛЕЙ САЙТА

Публикуем популярные вопросы от наших пользователей, оставленные в поле Комментариев. Прежде чем написать свой вопрос, проверьте: нет ли похожей задачи в начале статьи в разделе «Примеры решения задач» или среди вопросов в данном разделе!

Вопрос № 1. Длина стального листа 120 см, ширина 60 см, толщина 10 мм. Определить массу одного листа.

ОТВЕТ:≈ 56 кг.

Вопрос № 2. Какова масса платинового стержня, объём которого равен 21 дм³ ?

ОТВЕТ: 451,5 кг.

Вопрос № 3. Определить плотность бензина, если бак с бензином ёмкостью 20 литров имеет массу 14,2 кг?

Ответ: 710 кг/м³

Вопрос № 4. Масса бетонного блока, имеющего форму параллелепипеда, равна 12 кг. Какой станет масса блока, если одну его сторону увеличить в 2 раза, вторую – в 2,5 раза, а третью оставить без изменения?

ОТВЕТ: 60 кг.

Вопрос № 5. Сколько рейсов должен сделать самосвал грузоподъемностью 5 т, чтобы перевезти 100 м³ гранита? Плотность гранита 2600 кг/м³.

ОТВЕТ: 52 рейса.

Вопрос № 6. Плотность некоторого раствора 1300 кг/м³. После того как в этот раствор добавили 10 л воды (деминерализованной) плотность этого раствора стала 1290 кг/м³. Сколько литров раствора было с исходной плотностью?

ОТВЕТ: 290 литров.

---

Конспект урока по физике в 7 классе «Задачи на плотность, массу и объем с решением». Выберите дальнейшие действия:

• Перейти к теме: «ЗАДАЧИ на силу тяжести и вес тела».
• Вернуться к Списку конспектов по физике для 7-11 классов
• Найти конспект через Кодификатор ОГЭ по физике
• Найти конспект через Кодификатор ЕГЭ по физике

Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.

Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.

Сегодня мы познакомимся с такой характеристикой как плотность. Она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.

Связь массы, объема и вещества, из которого состоит тело

Рассмотрим опыт, представленный на рисунке 1.

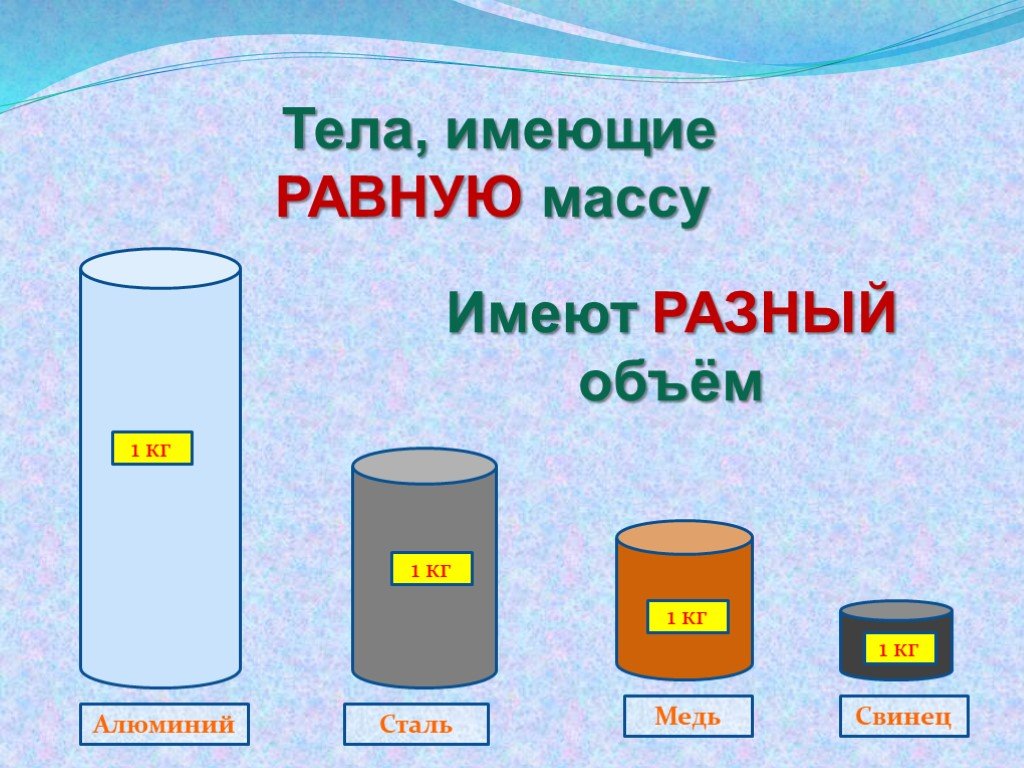
Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.

Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.

В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.

Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.

На рисунке изображены 2 тела массой $100 space г$: лед, железо и золото.

Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.

Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.

Определение плотности вещества

Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.

Рассмотрим два тела объемом $1 space м^3$ каждое. Если они будут состоять из разных веществ, то их массы тоже будут разными.

Итак, алюминий такого объема будет иметь массу 2700 кг, а свинец такого же объема ( $1 space м^3$) будет имеет массу 11 300 кг.

На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.

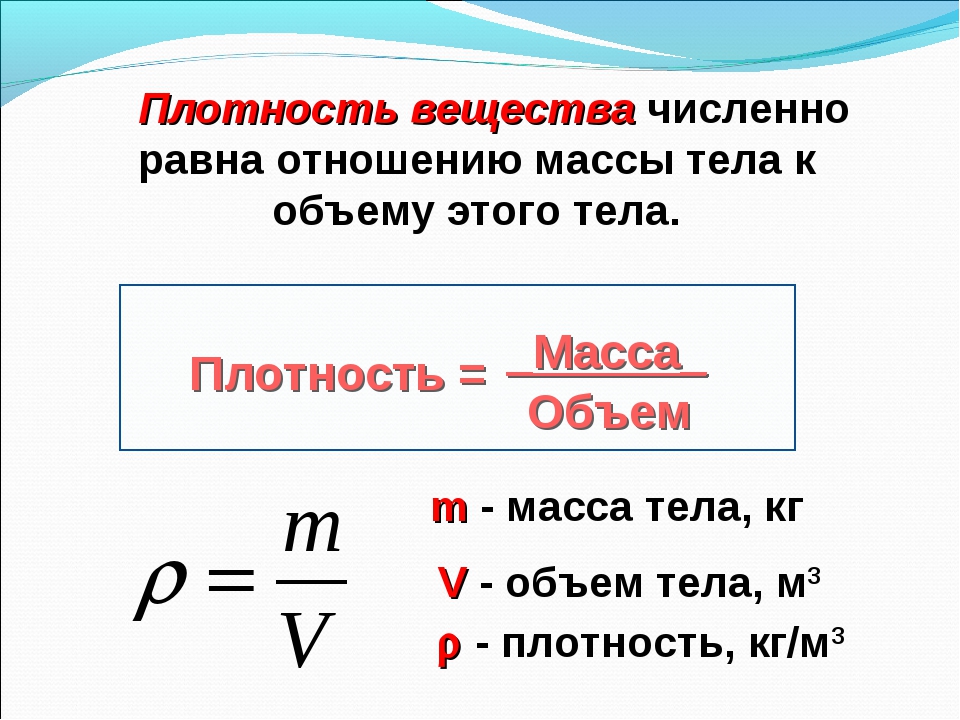
Плотность показывает, чему равна масса вещества, взятого в объеме  $1 space м^3$ (или  $1 space см^3$). Чтобы найти плотность вещества, нужно массу тела разделить на его объем.

По какой формуле можно рассчитать плотность вещества? Дадим определение.

Плотность  — это физическая величина, которая равна отношению массы тела к его объему:
$плотность = frac{масса}{объем}$
или
$rho = frac{m}{V}$,
где $rho$ (“ро”) — плотность вещества, $m$ — масса тела, $V$ — объем тела.

Единицы измерения плотности

Какова единица плотности в СИ?
В СИ плотность вещества измеряется в килограммах на кубический метр ($1 frac{кг}{м^3}$).

Какие еще единицы плотности вам известны?
Часто используется другая единица измерения — граммы на кубический сантиметр ($1 frac{г}{см^3}$) (рисунок 4).

Иногда нам потребуется переводить плотность веществ, выраженную в $frac{кг}{м^3}$ в $ frac{г}{см^3}$.

Давайте выразим плотность мрамора ($2700 frac{кг}{м^3}$) в $frac{г}{см^3}$:

$$rho = 2700 cdot frac{1 space кг}{1 space м^3} = 2700 cdot frac{1000 space г}{1 space 000 space 000 space см^3} = frac{2700}{1000} cdot frac{г}{см^3} = 2.7 frac{г}{см^3}$$

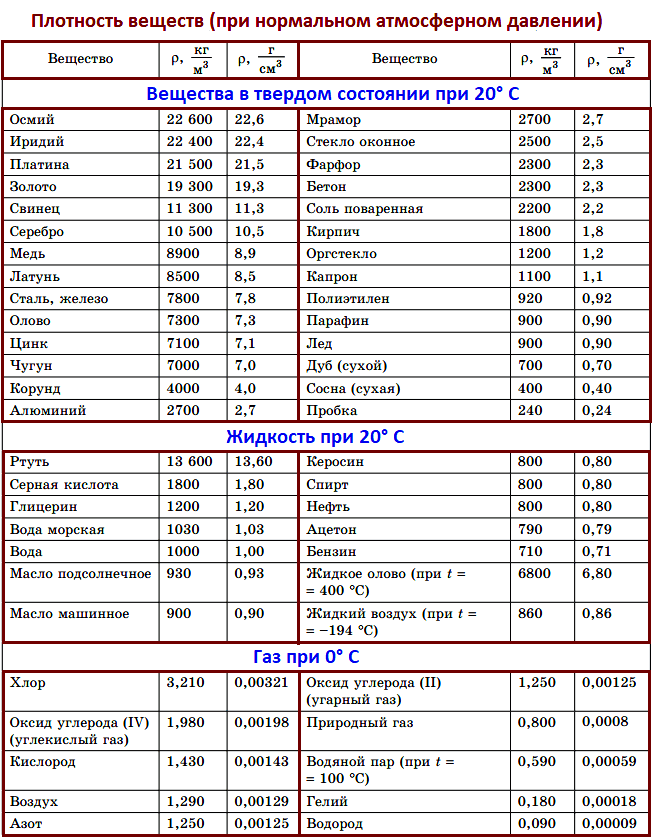
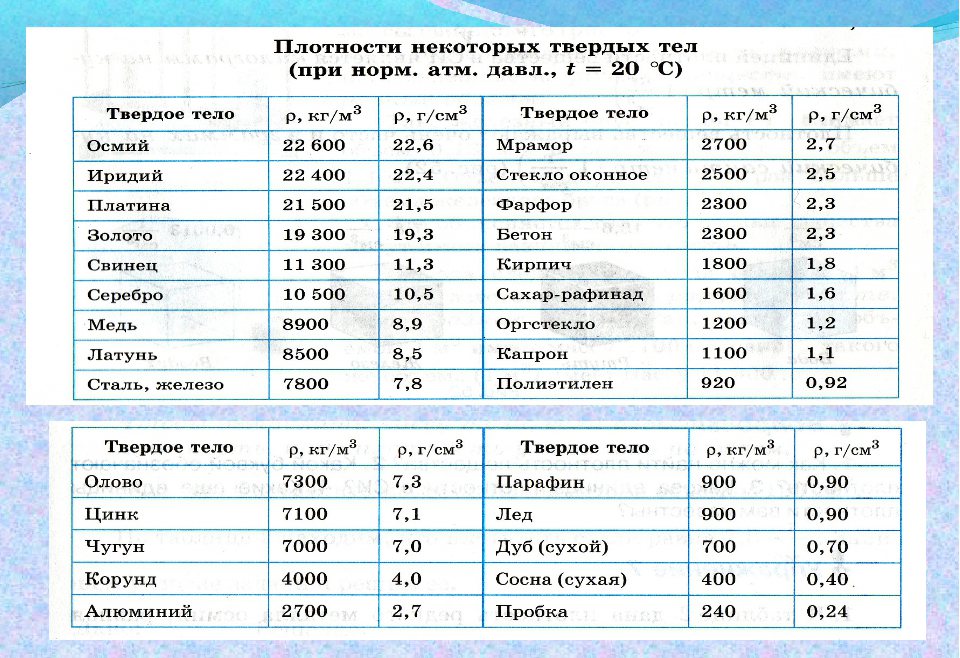
Таблицы плотности некоторых тел и веществ

Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна. 

Например, плотность воды составляет $1000 frac{кг}{м^3}$, льда — $900 frac{кг}{м^3}$, водяного пара — $0.590 frac{кг}{м^3}$ (рисунок 5).

Плотности различных твердых тел

Твердое тело	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Твердое тело	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Осмий	22 600	22,6	Мрамор	2700	2,7
Иридий	22 400	22,4	Стекло	2500	2,5
Платина	21 500	21,5	Фарфор	2300	2,3
Золото	19 300	19,3	Бетон	2300	2,3
Свинец	11 300	11,3	Кирпич	1800	1,8
Серебро	10 500	10,5	Сахар	1600	1,6
Медь	8900	8,9	Оргстекло	1200	1,2
Латунь	8500	8,5	Капрон	1100	1,1
Сталь, железо	7800	7,8	Полиэтилен	920	0,92
Олово	7300	7,3	Парафин	900	0,90
Цинк	7100	7,1	Лед	900	0,90
Чугун	7000	7,0	Дуб сухой	700	0,70
Корунд	4000	4,0	Сосна сухая	400	0,40
Алюминий	2700	2,7	Пробка	240	0,24

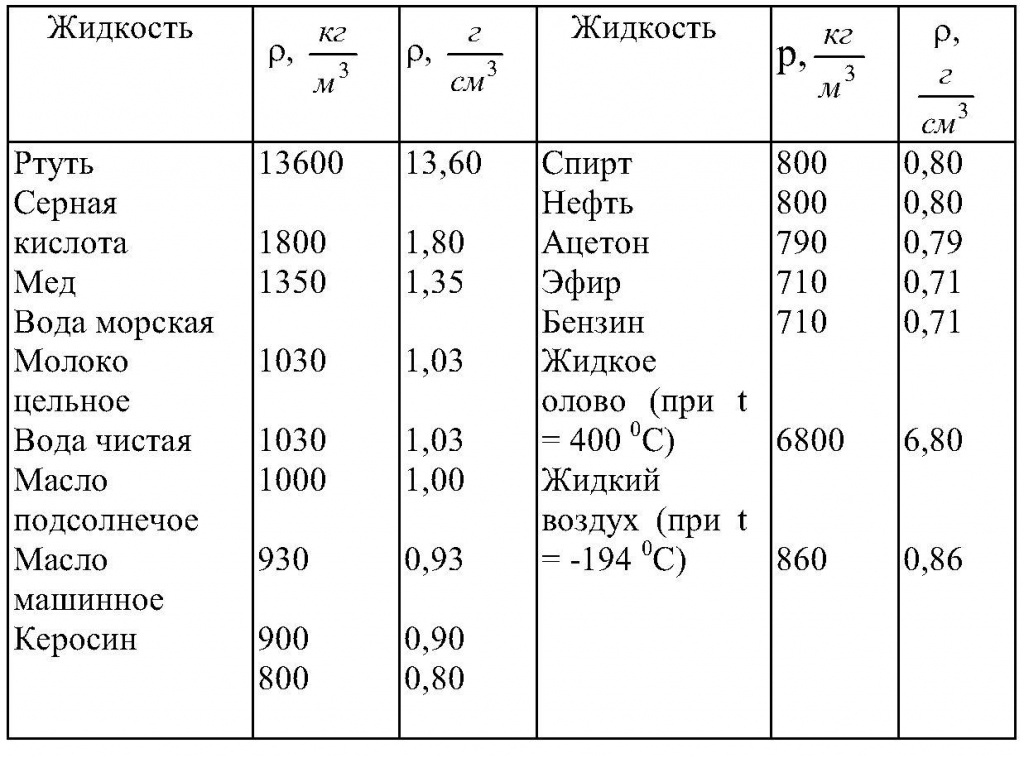
Плотности различных жидкостей

Жидкость	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Жидкость	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Ртуть	13 600	13,60	Керосин	800	0,80
Серная кислота	1800	1,80	Спирт	800	0,80
Мед	1350	1,35	Нефть	800	0,80
Вода морская	1030	1,03	Ацетон	790	0,79
Молоко цельное	1030	1,03	Эфир	710	0,41
Вода чистая	1000	1,00	Бензин	710	0,71
Масло подсолнечное	930	0,93	Жидкое олово (при $400^{circ}$)	6800	6,80
Масло машинное	900	0,90	Жидкий воздух (при $-194^{circ}$)	860	0,86

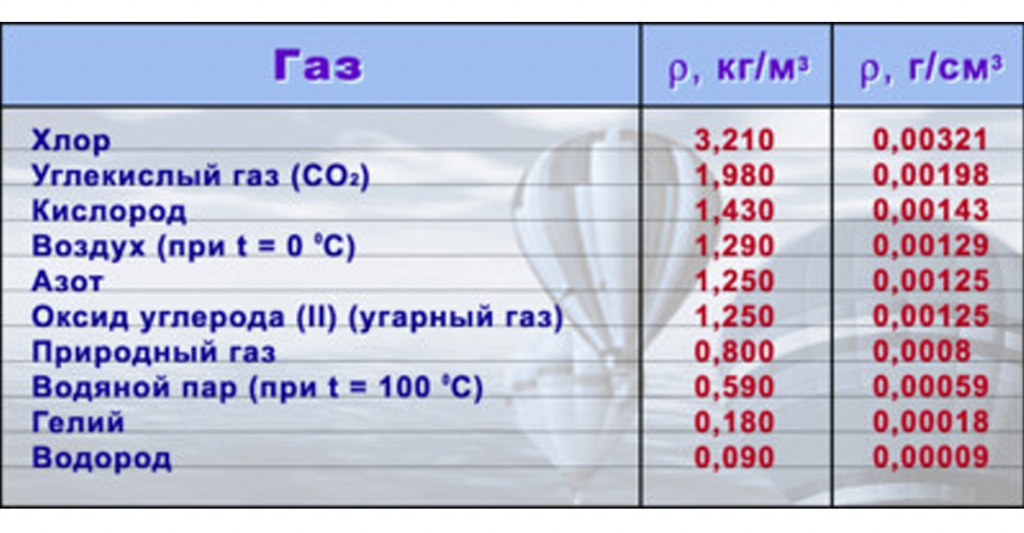
Плотности различных газов

Газ	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$	Газ	$rho, frac{кг}{м^3}$	$rho, frac{г}{см^3}$
Хлор	3,210	0,00321	Угарный газ	1,250	0,00125
Углекислый газ	1,980	0,00198	Природный газ	0,800	0,0008
Кислород	1,430	0,00143	Водяной пар (при $100^{circ}$)	0,590	0,00059
Воздух (при $0^{circ}C$	1,290	0,00129	Гелий	0,180	0,00018
Азот	1,250	0,00125	Водород	0,090	0,00009

Примеры задач на расчет плотности вещества

Посмотреть ответ

Скрыть

Переведем литры в кубические метры ($1 space л = 0.001 space м^3$): 
$30 cdot 0.001 = 0.03 space м^3$.

Дано:
$V = 30 space л$
$m =  21.3 space кг$

$rho -?$

Показать решение и ответ

Скрыть

Дано:
$а = 3 space м$
$b = 10 space см$
$c = 50 space см$
$m = 75 space кг$

$rho -?$

Показать решение и ответ

Скрыть

Больше задач с подробными решениями смотрите в отдельном уроке.

Упражнения

Посмотреть ответ

Скрыть

Показать ответ

Скрыть

Показать ответ

Скрыть

Дано:
$m = 12 space г$
$V = 100 space см^3$

$rho — ?$

Показать решение и ответ

Скрыть

Дано:
$а = 2.5 space см$
$b = 1 space см$
$с = 0.7 space см$
$m = 0.32 space г$

$rho — ?$

Показать решение и ответ

Скрыть

Взвесим шарик, мы узнаем его массу. Чтобы определить его объем, мы можем использовать измерительный цилиндр с водой. Для этого нужно опустить шарик в воду, и посмотреть, до какого уровня теперь поднялась воды. Разность этого объема и первоначального объема жидкости будет равна объему шарику.

Зная его массу и объем, мы сможем рассчитать его плотность по формуле: $rho = frac{m}{V}$.

Решение:

#239

Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!

Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.

Читать дальше!

Что такое формула плотности?

Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:

р = м / В

Где,

V – объем & m – масса объекта.

Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:

V = м / п

Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:

т = р * V

Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.

Как найти плотность объекта по массе и объему (шаг за шагом):

Рассчитать плотность с помощью этого расчет плотности очень просто. Вы можете найти любое из трех значений, введя два значения в формулу. Вот пример для каждого расчета:

Проведите по!

Пример:

Объект весил около 150 г и объем 90 см3. Найти плотность объекта?

Решение:

Формула:

р = м / В

Вот,

m = 150 г

V = 90 см3

Так,

р = 150/90

p = 1,66 г · см-3

как определить плотность объем по и массе:

Вы можете легко определить объем объекта, изменив уравнение плотности. Давайте посмотрим на пример:

Пример:

Какой у тела объем, если его масса 500 г, а плотность 4 см-3?

Решение:

Формула:

V = м / п

Вот,

м = 500г

р = 4 см-3

Так,

V = 500/4

V = 125 см3

Как найти массу объекта с учетом плотности и объема:

Расчет массы по объему и плотности становится простым. Просто следуйте следующему примеру:

Пример:

Объем объекта 200 см3, а плотность 9 см-3, какова масса объекта?

Решение:

Формула:

т = р * V

Вот,

V = 200 см3

р = 9 см-3

Так,

т = (9) * (200)

м = 1800г

Какая плотность воды?

Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:

Стол

Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.

Столы

Как пользоваться калькулятором плотности:

Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!

Входы:

• Прежде всего, выберите во вкладке то, что вам нужно найти.
• Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
• Наконец, нажмите кнопку “Рассчитать”.

Выходы:

Как только вы заполните все поля, калькулятор покажет:

• Плотность объекта
• Масса объекта
• Объем объекта
• Корень кубический из объема

Заметка:

Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.

Заключение:

Плотности широко используются для идентификации чистых веществ и определения состава различных видов смесей. В реальной жизни это полезно, когда выясняется, что что-то будет плавать в воде, и важно при расчете объема и массы вещества. Когда дело доходит до расчетов, запишите онлайн-калькулятор плотности, который поможет вам в кратчайшие сроки найти взаимосвязь между массой, объемом и плотностью вещества.

Others Languages:Density Calculator, Yoğunluk Hesaplama, Kalkulator Gęstości, Kalkulator Kepadatan, Dichte Rechner, 密度 計算, 밀도 계산, Výpočet Hustoty, Cálculo De Densidade, Calcul Densité, Calculadora De Densidad, Calcolo Densità, حساب الكثافة, Tiheys Laskuri, Massefylde Beregning, Tetthets Kalkulator.

Задача 1 

Определить плотность серной кислоты, если бидон емкостью 35 литров вмещает 63 кг кислоты

Задача 2

Металлическая деталь массой 949 г. имеет объем 130 куб. дм. Какой это металл? 

Задача 3

Чугунный шар имеет массу 70 кг, а объем 10 дм.³ Определить, сплошной этот шар или полый (с пустотами).

Задача 4

Масса чугунной плиты — 64 кг. Определить массу мраморной плиты таких же размеров.

Задача 5

Найдите плотность молока, если 206 г молока занимают объем 200 см³?

Задача 6

Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Задача 7

Определите плотность мела, если масса его куска объемом 20 см³ равна 48 г. Выразите эту плотность в кг/м³ и в г/см³.

Задача 8

Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

Задача 9

Брусок, масса которого 21,6 г. имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

Задача 10

Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

Задача 11

Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

Задача 12

Картофелина массой 59 г. имеет объем 50 см.³. Определите плотность картофеля и выразите ее в килограммах на кубический метр.

Задача 13

Подсолнечное масло объемом 1 литр имеет массу 920 грамм. Определите плотность масла. Выразите ее в килограммах на кубический метр.

Задача 14

Точильный брусок, масса которого 300 грамм, имеет размер 15*5*2 см. Определите плотность вещества из которого он сделан.

Задача 15

Какая из двух ложек одинаковой массы — стальная или серебряная — имеет большие размеры?

Задача 16

Из какого металла может быть изготовлен деталь, если ее масс 3,9 кг., а объем 500 см.³?

Задача 17

Сплав состоит из олова массой 2,92 кг. и свинца массой 1,13 кг. Какова плотность сплава, если считать, что объем сплава равен сумме объемов его составных частей?

Задача 18

Какова плотность бензина, если 12 литров имеют массу 8,52 кг.?

Задача 19

В пол литровую бутылку налито 465 грамм подсолнечного масла. Какова плотность масла?

Задача 20

Тщательным совместным растиранием смешали по 100 г парафина, буры и воска. Какова средняя плотность получившейся смеси, если плотность этих веществ равна соответственно 0,9 г/см³, 1,7 г/см ³, 1 г/см³ ?

Задача 21

Определите плотность стекла из которого сделан куб массой 857,5 г, если площадь всей поверхности куба равна 294 см². 

Задача 22

В сообщающиеся сосуды налита ртуть. В один сосуд добавили воду, высота столба которого 4 см. Какой высоты должен быть столб некоторой жидкости в другом сосуде, чтобы уровень ртути в обоих сосудах был одинаков, если плотность жидкости в 1,25 раза меньше плотности воды?  

Задача 23

Вес тела в воде в 2 раза меньше, чем в воздухе. Какова плотность вещества тела?

Задача 24

Тело весит в воздухе 3 Н, в воде 1,8 Н и в жидкости неизвестной плотности 2,04 Н. Какова плотность этой неизвестной жидкости? 

Задача 25

В заброшенном парке дети откопали слиток. На нем было выгравировано старинными буквами, что слиток состоит из двух частей золота и трех частей серебра, и его объем составляет V=357 см³ . Какова масса слитка?

Задача 26
В цирке клоун одной левой поднимает огромную гирю, на которой написано 500 кг. На самом деле масса гири в сто раз меньше. Объем этой гири 0,2 м³. Вычисли плотность цирковой гири.

Задача 27

Печальный дядя Боря хотел сам сварить себе суп, и у него получилось пол кастрюли зеленой гадости. Объем этой гадости, которую дядя Боря не отважился попробовать, 0,001 м³.
Масса этого кубического дециметра гадости 1 кг 300 г. Вычисли плотность дяди Бориной гадости.

Задача 28

Ученый с мировым именем Иннокентий решил плотно пообедать и с аппетитом съел комплексный обед из трех блюд. Масса первого блюда — 550 граммов, объем — 0,0005 м³. Масса второго — 150 грамм, объем — 0,0002 м³.

Задача 29

Масса компота — 1 кг 100 грамм, объем — 0,0011 м³. Как вычислить среднюю плотность плотного обеда, который ученый с мировым именем съел без хлеба?

Задача 30

После того как трое мышей на дне рождения мышки Мушки угостились одним крупным куском хозяйственного мыла, их общая масса увеличилась на 540 г. Мыло до того, как мыши его съели, имело размеры 10 см, 12 см, 3 см. Определите плотность уже не существующего мыла.

Задача 31

Стакан, заполненный до краев водой, имеет массу m¹ = 214,6 г. Когда в этот стакан с водой поместили небольшой камень массой 29,8 г и часть воды вылилась наружу, масса стакана с содержимым оказалась равной m² = 232 г.  Определить плотность вещества камня.

Задача 32

В сосуд, заполненный водой, бросают кусок  алюминиевого сплава. После того, как часть воды вылилась из сосуда, масса его с оставшейся водой и куском сплава увеличилась на 25 г. Когда вместо воды использовали жидкое масло плотностью 0,9 г/см.³ и повторили измерения, то масса сосуда с маслом и куском сплава увеличилась на 26 г. Определите плотность сплава.

Задача 33

Какая жидкость налита в емкость объемом 125 л, если ее масса оказалась равной 88 кг 750 г.?

Задача 34Котелок ёмкостью 3 литра плотно набили снегом и повесили над костром. Когда снег растаял, котелок оказался на 1/4 своего объёма наполнен водой. Какова была плотность снега в котелке, если плотность воды составляет ρ = 1000 кг/м³? Ответ выразить в кг/м³.

Задача 35

Скульптор изваял три фигуры одинаковой массы из мрамора, сухого дуба и льда. Определите, из какого вещества сделана каждая фигура.

Задача 36

Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

Задача 37

Определить объем оловянного бруска массой 146 г.

Задача 38

Вычислите массу тела по его плотности и объему.

Вещество	Плотность вещества p, г/см3	Объем тела V, см3	Масса тела m, г
Полученная экспериментально	Вычисленная по формуле
картофель	0,67	48

Задача 39

Вычислите объем тела по его плотности и массе.

Вещество	Плотность вещества p, г/см3	Объем тела V, см3	Масса тела m, г
Получено экспериментально	Вычислено по формуле
пластилин	1,4			16,2

Задача 40

Определите объем кирпича, если его масса 5 кг?

Задача 41

Определите массу стальной детали объёмом 120 см³

Задача 42

Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Задача 43

Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

Задача 44

В куске кварца содержится небольшой самородок золота. Масса куска равна 100 г, а его средняя плотность 

 г/см

. Определите массу золота, содержащегося в куске кварца, если плотность кварца 2,65 г/см

, а плотность золота 19,4 г/см³.

Задача 45

Для накачивания керосина в бак используется насос производимостью 20 кг в минуту. Определите время, необходимое для наполнения бака,если его длина 2 м, ширина 150 см, высота 1800 мм.

Задача 46

Золото можно расплющить до толщины 0,0001 мм. Какую площадь поверхности металла (или дерева) можно покрыть такими пластинками, изготовленными из золота массой 2,316 г. Плотность золота 19,3 г/см

Задача 47

В чистой воде растворена кислота. Масса раствора 240 г, его плотность 1,2 г/см³. Определите массу кислоты, содержащейся в растворе, если плотность кислоты 1,8 г/см³. Принять объем раствора равным сумме объема его составных частей. Плотность воды 1 г/см³.

Задача 48

В воздушный шарик накачали порцию воздуха. При этом масса возросла в 4 раза, а объём – вдвое. Во сколько раз возросла плотность воздуха в шарике?

Задача 49

Подсчитайте, во сколько раз отличаются плотности воды и спирта.

Задача 50

Найдите ошибку в рассуждении: плотность 1 м³ керосина 800 кг/м³. Тогда плотность 2 м³ керосина будет 1600 кг/м³.

Задача 51

Для измерения плотности пластилина взяли его кусок массой 100 г. Как изменятся результаты измерений, если будет взят кусок массой 200 г

Задача 52

Чтобы отлить бетонный фундамент, вырыли траншею объёмом 2 м³. Для её заполнения влили 4800 кг бетона. Вычислите плотность бетона.

Задача 53

Объём одной комнаты в квартире равен 40 м³. Какую массу имеет воздух, находящийся в комнате?

Задача 54

Чтобы заполнить банку доверху, потребовалось 4,1 кг меда. Вычислите объём банки.

Задача 55

Масса шара объёмом 1,5 м³ составляет более 3 т. Верно ли, что плотность вещества шара более 2 т/м³?

Задача 56

Объём куба массой 80 кг составляет более 10 дм³. Правда ли, что металл, из которого сделан куб, имеет плотность более 80 кг/дм³?

Задача 57

Плотность золота 19 г/см³. Верно ли, что золотой кубик с объёмом более 10 см³ будет иметь массу более 100 г?

Задача 58

Плотность мёда 1,35 г/см³. Правда ли, что порция мёда при объёме более 100 см³ будет иметь массу более 200 г?

Задача 59

Верно ли, что объём воздуха массой 13 кг более 10 м³?

Задача 60

Верно ли, что водород массой менее 1 кг имеет объём более 10 м³?

Задача 61

Плотность вещества картофеля составляет 1,2 г/см³. Выразите это значение в кг/м³. Почему это значение намного больше табличного?

Задача 62

В кастрюлю объёмом 7,3 л положили 5,7 кг картофеля и доверху залили водой. Ее понадобилось 2,3 л. Найдите плотность картофелины.

Задача 63

Имеются ли пустоты в чугунной отливке (литой детали) массой 34 кг, если объём формы для литья был 5 дм³?

Задача 64

После рейса в бензобаке автобуса осталось более 50 кг бензина. Что можно сказать про объём бензобака?

Задача 65

Масса канистры, заполненной машинным маслом, равна 19,5 кг. Масса пустой канистры 1,5 кг. Каков её объём?

Задача 66

Трёхлитровую стеклянную банку наполовину заполнили мёдом. На сколько увеличилась масса банки?

Задача 67

Площадь пола овощехранилища равна 40 м², а высота слоя картофеля не должна превышать 60 см. Какая масса картофеля может находиться в таком овощехранилище?

Задача 68

Вычислите, поместится ли в большой 120-литровой алюминиевой бочке 110 кг спирта?

Задача 69

Сколько воды выльется из полного стеклянного сосуда при всыпании в него 340 г свинцовой дроби?

Задача 70

В кружку с 50 г мёда долили ещё 200 мл молока. На сколько возросла масса кружки?

Задача 71

В банку опустили свинцовый шар объёмом 20 см³ и долили 100 мл керосина. На сколько возросла масса банки?

Задача 72

Изготовили ящик объемом 3 м³. Насыпав в него песка, обнаружили, что ящик заполнен на четверть. На сколько увеличилась масса ящика?

Задача 73

В мензурку, где находится 150 мл воды, опускают стальной кубик массой 10 г. На сколько увеличится объём содержимого мензурки?

Задача 74

В мензурку, где находится 150 мл воды, опускают стальной кубик массой 10 г. До какой отметки поднимется уровень воды в мензурке?

Задача 75

На какой отметке будет уровень воды в мензурке при вливании туда 100 г воды и 100 г подсолнечного масла?

Задача 76

На какой отметке установится уровень воды в мензурке при вливании туда 100 г воды и 100 мл ртути?