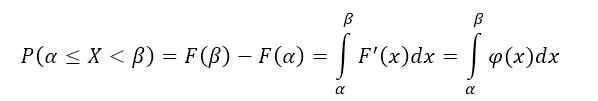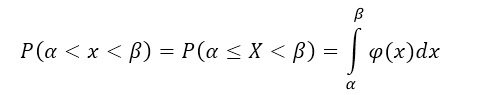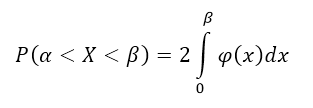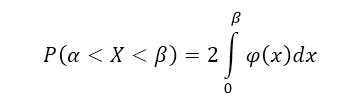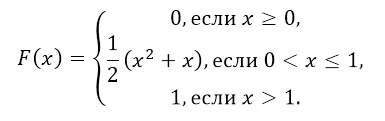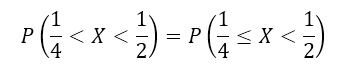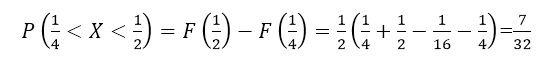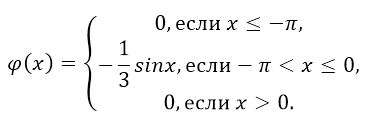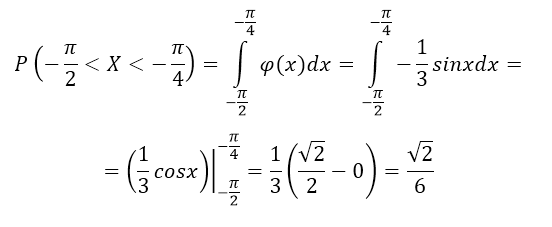Как найти плотность вероятности на интервале - Исправление недочетов и поиск решений вместе с Examum.ru

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

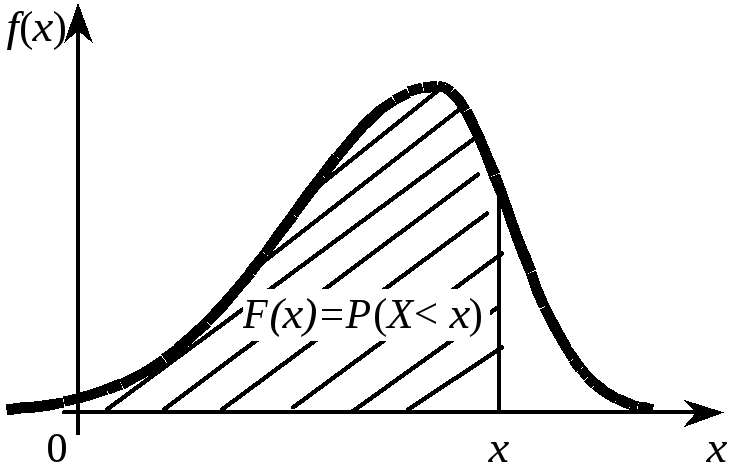
Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

— функцию
распределения вероятностей;

—
математическое ожидание;

—
дисперсию;

— среднее
квадратическое отклонение;

— вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

—
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

—
составить функцию плотности распределения и построить ее график;

— найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

— найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Непрерывная
случайная величина может быть задана
не только с помощью функции распределения.
Введем понятие плотности
вероятности
непрерывной случайной величины.

Рассмотрим
вероятность попадания непрерывной
случайной величины на интервал [х,
х
+ Δх].
Вероятность такого события

P(х
≤ X
≤ х
+ Δх)
= F(х+
Δх)
– F(х),

т.е.
равна приращению функции распределения
F(х)
на этом участке. Тогда вероятность,
приходящаяся на единицу длины, т.е.
средняя плотность вероятности на участке
от х
до х+
Δх,
равна

Переходя к пределу
Δх
→ 0, получим плотность вероятности в
точке х:

представляющую
производную функции распределения
F(х).
Напомним, что для непрерывной случайной
величины F(х)
– дифференцируемая функция.

Определение.
Плотностью
вероятности
(плотностью
распределения)
f(x)
непрерывной
случайной величины Х называется
производная ее функции распределения

f(x)
= F′(x).

(4.8)

Про случайную
величину Х
говорят, что она имеет распределение с
плотностью f(x)
на определенном участке оси абсцисс.

Плотность вероятности
f(x),
как и функция распределения F(x)
является одной из форм закона распределения.
Но в отличие от функции распределения
она существует только для непрерывных
случайных величин.

Плотность вероятности
иногда называют дифференциальной
функцией
или дифференциальным
законом распределения.
График плотности вероятности называется
кривой
распределения.

Пример 4.4.
По данным примера 4.3 найти плотность
вероятности случайной величины Х.

Решение.
Будем находить плотность вероятности
случайной величины как производную от
ее функции распределения f(x)
= F‘(x).

◄

Отметим свойства
плотности вероятности непрерывной
случайной величины.

1.
Плотность
вероятности – неотрицательная функция,
т.е.

f(x)
≥ 0,

(4.9)

как
производная монотонно неубывающей
функции F(x).

2.
Вероятность
попадания непрерывной случайной величины
Х в интервал [α,
β,]
равна
определенному интегралу от ее плотности
вероятности в пределах от α
до β,
т.е.

(4.10)

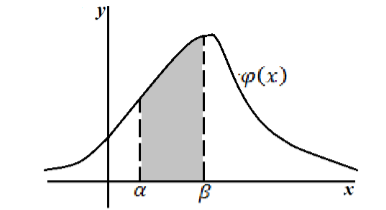
Геометрически
вероятность попадания в интервал [α,
β,]
равна площади фигуры, ограниченной
сверху кривой распределения и опирающейся
на отрезок [α,
β,]
(рис.4.4).

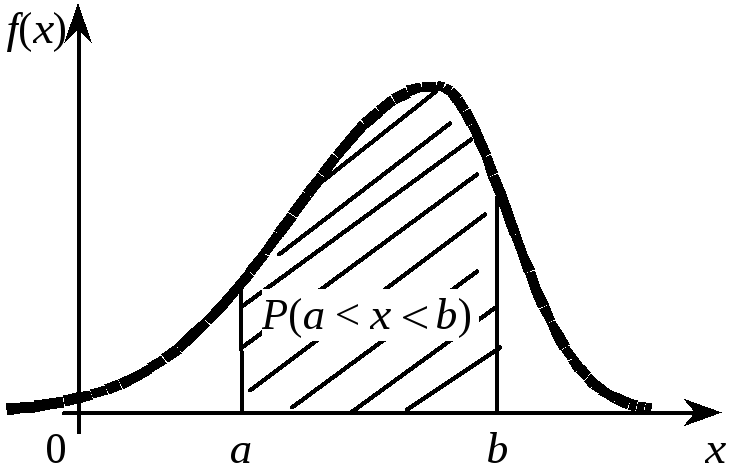
Рис. 4.4 Рис.
4.5

3.
Функция
распределения непрерывной случайной
величины может быть выражен через
плотность вероятности по формуле:

.	(4.11)

Геометрически
функция распределения равна площади
фигуры, ограниченной сверху кривой
распределения и лежащей левее точки х
(рис. 4.5).

4.
Несобственный
интеграл в бесконечных пределах от
плотности вероятности непрерывной
случайной величины равен единице:

.	(4.12)

Геометрически
свойства 1
и 4
плотности вероятности означают, что ее
график – кривая распределения – лежит
не ниже оси абсцисс, а полная площадь
фигуры, ограниченной кривой распределения
и осью абсцисс, равна единице.

Пример 4.5.
Функция f(x)
задана в виде:

Найти: а) значение
А;
б) выражение функции распределения
F(х);
в) вероятность того, что случайная
величина Х
примет значение на отрезке [0; 1].

Решение.
а) Для того, чтобы f(x)
была плотностью вероятности некоторой
случайной величины Х,
она должна быть неотрицательна,
следовательно, неотрицательным должно
быть и значение А.
С учетом свойства 4
находим:

,
откуда А
=
.

б) Функцию
распределения находим, используя
свойство 3:

Если x
≤ 0, то f(x)
= 0 и, следовательно, F(x)
= 0.

Если 0 < x
≤ 2, то f(x)
= х/2
и, следовательно,

Если х
> 2, то f(x)
= 0 и, следовательно

в) Вероятность
того, что случайная величина Х
примет значение на отрезке [0; 1] находим,
используя свойство 2:

=
0,25. ◄

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Пусть нам задана функция плотности распределения непрерывной случайной величины. Тогда с её помощью мы можем найти вероятность того, что случайная величина попадет в интервал $(alpha ,beta )$.

Для начала вспомним несколько свойств функции распределения вероятности $F(x)$, которые понадобятся нам в дальнейшем.

Свойство 1: Для любых $X$ выполняется равенство:

Сформулируем и докажем следующую теорему:

Вероятность того, что непрерывная случайная величина $X$ примет значение из интервала $(alpha ,beta )$ равна значению определенного интеграла от $alpha $ до $beta $ плотности распределения $varphi (x)$.

Доказательство.

Используя свойство 1, имеем:

[Pleft(alpha le XИспользуя формулу Ньютона-Лейбница, получим:

Рисунок 1.

Так как случайная величина $X$ непрерывна, то и функция распределения $F(x)$ также непрерывна. Следовательно, по свойству 2, получим:

Рисунок 2.

ч. т. д.

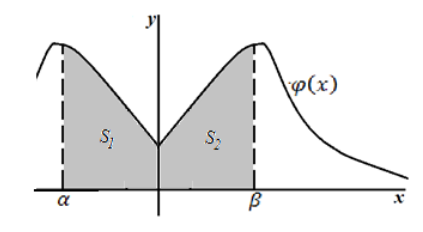
Геометрически данную теорему можно интерпретировать следующим образом: Вероятность попадания случайной непрерывной величины $X$ в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной кривыми $y=varphi left(xright), x=alpha ,$ $x=beta $ и $y=0$ (рис. 1).

Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.

Следствие 1: Если плотность распределения $varphi (x)$ — четная функция, а значения $alpha и beta $ равны по абсолютной величине (по модулю), причем $alpha ne beta $, то вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ можно найти по формуле:

Рисунок 4.

«Вероятность попадания непрерывной величины в заданный интервал » 👇

Этот факт может быть легко показан геометрически:

Рисунок 5.

Очевидно, что $S_1=S_2$.

Используя геометрический смысл плотности распределения, и получаем, что

Рисунок 6.

Примеры задач на нахождение вероятности попадания непрерывной случайной величины в заданный интервал

Пример 1

Функция распределения имеет вид:

Рисунок 7.

Найти вероятности попадания случайной величины в интервал $(frac{1}{4},frac{1}{2})$.

Решение: Очевидно, что функция $F(x)$ непрерывна на сей области определения (в том числе непрерывна справа на всем интервале $(frac{1}{4},frac{1}{2})$). Значит по свойству 2, получим

Рисунок 8.

Теперь, пользуясь свойством 1, получим:

Рисунок 9.

Ответ: $frac{7}{32}$.

Пример 2

Плотность распределения задана в виде:

Рисунок 10.

Найти вероятности попадания случайной величины в интервал $(-frac{pi }{2},-frac{pi }{4})$.

Решение: Используя теорему 1, получим:

Рисунок 11.

Ответ: $frac{sqrt{2}}{6}$.

Пример 3

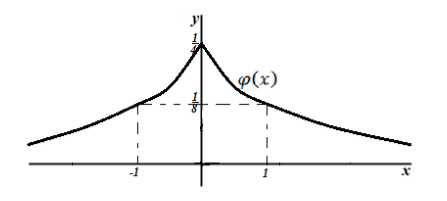
Функция плотности распределения имеет вид:

[varphi left(xright)=frac{1}{4x^2+4}]

Построить график плотности распределения и найти вероятность попадания случайной величины в интервал $left(-2,2right).$

Решение: Построим график функции $varphi left(xright)$:

Рисунок 12.

Функция $varphi left(xright)$ четна, концы интервала $left(-2,2right)$ симметричны относительно начала координат, следовательно, по следствию 1, получаем:

[Pleft(-2Ответ: $frac{1}{2}arctg2.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник