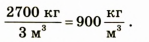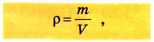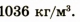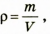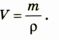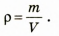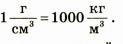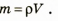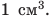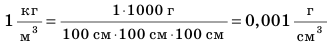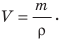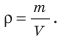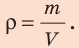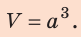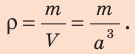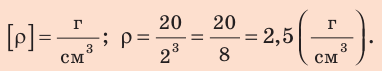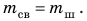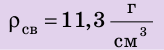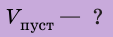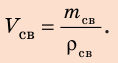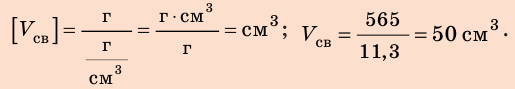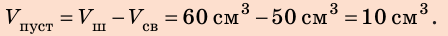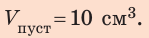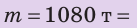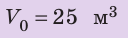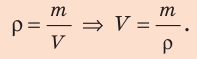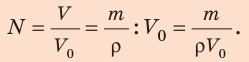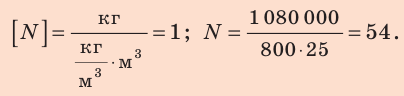Как найти плотность вещества бруска

Цель работы: Научиться определять
плотность твердого тела.

Приборы и материалы:

1. Весы с разновесами;
2. Линейка ученическая;
3. Твердые тела, плотность, которых надо
   определять.

Теория.

Плотность – это физическая величина, которая
равна отношению массы тела к его объему: (1)

В СИ единицей плотности является килограмм на
кубический метр:

Очень часто плотность вещества выражается в
граммах на кубический сантиметр:

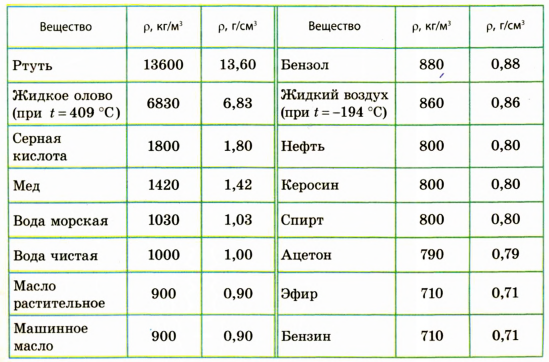
Например: Вода имеет плотность 1
гсм³; ртуть – 13600 гсм³; железо – 7, 8
гсм³; воздух – 0,0013 гсм³.

Пример: Плотность чугуна 7000 кгм³.
Выразите ее в гсм³.

Сначала килограммы переведем в граммы, а
кубические метры в кубические сантиметры: р =
7000кгм³ = 7000 *1000 кг10⁶ см³ = 7 гсм³.

Плотность одного и того же вещества в твердом,
жидком и газообразном состояниях различна.

Работа №1. Определение плотности вещества
брусков.

Определить плотность брусков из древесины,
пластмассы и металлов.

Указания к работе.

1. Напишите формулу (1) и обдумайте, что нужно
   измерять для определения плотности вещества.
   Составьте таблицу для занесения результатов
   измерений и вычислений.
2. Измерьте массу тел.
3. Измерьте размеры тел и определите их объем.
4. Рассчитайте по формуле (1) плотность данных тел.
5. Результаты измерений и вычислений занесите в
   таблицу 1.
6. Сравните полученные результаты с данными из
   таблиц плотностей.
7. Оцените погрешности вычислений физических
   величин.
8. Ответьте на следующие вопросы:

— Плотность воды 1000 кгм³ . Что это
означает?
— Как можно определить наличие пустот в телах,
если известно из какого вещества они сделаны?

Таблица №1. Параметры брусков.

Таблица №2. Плотность вещества
брусков.

Работа №2. Определение плотности вещества
тела в форме параллелепипеда со сквозной
цилиндрической выемкой.

Определить плотность деревянного тела в форме
параллелепипеда со сквозной цилиндрической
выемкой.

Указания к работе.

1. Напишите формулу (1) и обдумайте, что нужно
   измерять для определения плотности вещества
   твердого тела.
2. Измерьте массу тела.
3. Измерьте размеры тела и определите его объем.
4. Измерьте радиус и высоту воздушного цилиндра в
   теле. Вычислить объем воздушного цилиндра.
5. Вычислите объем древесины.
6. Рассчитайте плотность древесины по формуле (1).
7. Результаты измерений и вычислений занесите в
   таблицы № №1,2,3.
8. Определите сорт древесины по таблице
   плотностей.
9. Оцените погрешности физических величин.
10. Решите задачу (1): Кусок металла массой 461,5 г
    имеет объем 65 см3. Что это за металл?

Таблица №1. Параметры бруска.

Таблица №2. Параметры воздушного
цилиндра.

Таблица №3 Плотность вещества
твердого тела.

Работа №3 Определение плотности вещества тела
в форме параллелепипеда с шестью
цилиндрическими выемками.

Указания к работе.

1. Напишите формулу (1) и обдумайте, что нужно
   измерять для определения плотности данного
   твердого тела.
2. Измерьте массу тела.
3. Измерьте размеры тела и определите его объем.
4. Измерьте радиус и высоту воздушных цилиндров в
   теле. Определите их суммарный объем.
5. Вычислите объем древесины.
6. Рассчитайте плотность древесины по формуле (1).
7. Результаты измерений и вычислений занесите в
   таблицу №№ 1,2,3.
8. Оцените погрешности физических величин.
9. Решите задачу (1): Три кубика – из мрамора, льда и
   латуни имеют одинаковый объем. Какой из них имеет
   большую массу, а какой меньшую.

Таблица №1 Параметры бруска.

Таблица №2. Параметры воздушных
цилиндров.

Таблица №3. Плотность вещества
тела.

Задачи(1,2,5).

1. Чугунный шар при объеме 125 см³ имеет массу
   800 г. Сплошной или полый этот шар?
2. Картофелина массой 59 г. имеет объем 50 см³.
   Определите плотность картофеля и выразите ее в
   килограммах на кубический метр (кгм³).
3. Из какого металла изготовлена втулка
   подшипника, если ее масса 3,9 кг, а объем 500 см³?
4. Точильный брусок, масса которого 300 г, имеет
   размер 15*5*2 см. Определите плотность вещества, из
   которого он сделан.
5. Определите массу мраморной плиты, размер
   которой 1,0*0,8*0,1 м.
6. Как определить плотность неизвестной жидкости,
   используя только стакан, воду и весы с
   разновесом?
7. Как определить плотность неизвестной жидкости,
   используя стакан и весы с разновесом из латуни?
8. Деталь, отлитая из меди, имеет массу М. Какую
   массу m имела деревянная модель детали, если
   известны плотности меди и дерева?
9. Начертите график зависимости плотности воды
   данной массы от температуры. Температура воды
   изменяется от 0 до 8⁰ С.
10. Начертите график зависимости объема воды
    данной массы от температуры. Температура воды
    изменяется от 0 до 8⁰ С.

Литература:

1. Лукашик В.И. Сборник задач по физике 7-8 класс,
   Москва, “Просвещение”, 1994.
2. Лукашик В.И. Физическая олимпиада. Москва,
   “Просвещение”, 1999.
3. Мякишев Г.Я., Буховцев Б.Б. Физика 10 класс, Москва,
   “Просвещение”, 2000.
4. Перышкин А.В. Физика, 7 класс, Москва, “Дрофа”,
   2004.
5. Рымкевич А.П. Сборник задач по физике. Москва,
   “Просвещение”. 2000.

Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!

Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.

Читать дальше!

Что такое формула плотности?

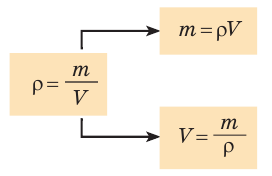
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:

р = м / В

Где,

V – объем & m – масса объекта.

Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:

V = м / п

Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:

т = р * V

Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.

Как найти плотность объекта по массе и объему (шаг за шагом):

Рассчитать плотность с помощью этого расчет плотности очень просто. Вы можете найти любое из трех значений, введя два значения в формулу. Вот пример для каждого расчета:

Проведите по!

Пример:

Объект весил около 150 г и объем 90 см3. Найти плотность объекта?

Решение:

Формула:

р = м / В

Вот,

m = 150 г

V = 90 см3

Так,

р = 150/90

p = 1,66 г · см-3

как определить плотность объем по и массе:

Вы можете легко определить объем объекта, изменив уравнение плотности. Давайте посмотрим на пример:

Пример:

Какой у тела объем, если его масса 500 г, а плотность 4 см-3?

Решение:

Формула:

V = м / п

Вот,

м = 500г

р = 4 см-3

Так,

V = 500/4

V = 125 см3

Как найти массу объекта с учетом плотности и объема:

Расчет массы по объему и плотности становится простым. Просто следуйте следующему примеру:

Пример:

Объем объекта 200 см3, а плотность 9 см-3, какова масса объекта?

Решение:

Формула:

т = р * V

Вот,

V = 200 см3

р = 9 см-3

Так,

т = (9) * (200)

м = 1800г

Какая плотность воды?

Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:

Стол

Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.

Столы

Как пользоваться калькулятором плотности:

Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!

Входы:

• Прежде всего, выберите во вкладке то, что вам нужно найти.
• Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
• Наконец, нажмите кнопку “Рассчитать”.

Выходы:

Как только вы заполните все поля, калькулятор покажет:

• Плотность объекта
• Масса объекта
• Объем объекта
• Корень кубический из объема

Заметка:

Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.

Заключение:

Плотности широко используются для идентификации чистых веществ и определения состава различных видов смесей. В реальной жизни это полезно, когда выясняется, что что-то будет плавать в воде, и важно при расчете объема и массы вещества. Когда дело доходит до расчетов, запишите онлайн-калькулятор плотности, который поможет вам в кратчайшие сроки найти взаимосвязь между массой, объемом и плотностью вещества.

Others Languages:Density Calculator, Yoğunluk Hesaplama, Kalkulator Gęstości, Kalkulator Kepadatan, Dichte Rechner, 密度 計算, 밀도 계산, Výpočet Hustoty, Cálculo De Densidade, Calcul Densité, Calculadora De Densidad, Calcolo Densità, حساب الكثافة, Tiheys Laskuri, Massefylde Beregning, Tetthets Kalkulator.

Тела, состоящие из различных веществ, при одинаковой массе будут иметь различные объемы, а при одинаковых объемах — различные массы. Происходит это из-за того, что каждое вещество имеет определенную плотность, которая описывается формулой $rho = frac{m}{V}$.

На данном уроке мы рассмотрим задачи на нахождение массы, объема или плотности по другим известным параметрам тел и их подробные решения. Вам понадобятся табличные значения плотностей различных веществ, из которых состоят тела, — их вы можете найти здесь.

Задача №1

Определите массу бензина, спирта, меда объемом $10 space л$.

$m_б, m_с, m_м — ?$

Показать решение и ответ

Скрыть

Задача №2

Медная кастрюля имеет массу $0.5 space кг$. Если кастрюлю такого же размера изготовить из стали, какая у нее будет масса?

Дано:
$m_1 = 0.5 space кг$
$rho_1 = 8900 frac{кг}{м^3}$
$rho_2 = 7800 frac{кг}{м^3}$
$V_1 = V_2 = V$

$m_2 — ?$

Показать решение и ответ

Скрыть

Задача №3

Металлический кусок имеет объем $200 space см^3$ и массу $540 space г$. Из какого металла этот кусок? Какова его плотность?

Дано:
$V = 200 space см^3$
$m = 540 space г$

$rho — ?$

Показать решение и ответ

Скрыть

Задача №4

Вычислите массу чугунного бруска с внутренней выемкой (рисунок 1).

Дано:
$a = 5 space см$
$b = 3 space см$
$c = 2 space см$
$a_1 = 2 space см$
$b_1 = 1 space см$
$rho = 7 frac{г}{см^3}$

Показать решение и ответ

Скрыть

Задача №5

Емкость бадьи для бетона $1.5 space м^3$. Такая емкость выбрана для того, чтобы ее масса с бетоном не превышала грузоподъемности подъемного крана, которая равна $5 space т$. Определите плотность бетона, если вес самой бадьи $1.7 space т$.

$rho — ?$

Показать решение и ответ

Скрыть

Задача №6

Мензурка, до краев наполненная спиртом, имеет массу $500 space г$. Та же мензурка без спирта имеет массу $100 space г$. Какой объем вмещает мензурка?

Дано:
$m = 500 space г$
$m_1 = 100 space г$
$rho = 0.8 frac{г}{см^3}$

$V — ?$

Показать решение и ответ

Скрыть

Один из самых легких металлов — магний — является главной составной частью сплава, которая называется “электрон-металл”, имеющего применение в авиастроении. Плотность этого сплава $1.8 frac{г}{см^3}$. Во сколько раз предмет, изготовленный из электрон-металла, будет легче такого же размера изделия из стали?

Дано:
$rho = 1.8 frac{г}{см^3}$
$rho_с = 7.8 frac{г}{см^3}$

$frac{m_с}{m} — ?$

Показать решение и ответ

Скрыть

Задача №8

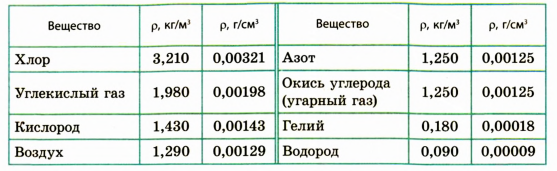
Газовый баллон имеет объем $30 space дм^3$. Его наполняют газом, обращенным в жидкое состояние. Рассчитайте, сколько в баллоне помещается килограммов жидкого хлора, плотность которого $1.2 frac{г}{см^3}$. Сколько получится при выпуске литров газообразного хлора, плотность которого $0.0032 frac{г}{см^3}$?

Дано:
$V_1 = 30 space дм^3 = 30 cdot 10^3 space см^3$
$rho_1 = 1.2 frac{г}{см^3}$
$rho_2 = 0.0032 frac{г}{см^3}$

$m — ?$
$V_2 — ?$

Показать решение и ответ

Скрыть

Задача №9

Ртуть и нефть одинаковой массы налили в разные емкости. Во сколько раз объем, занимаемой ртутью, меньше объема, занимаемого нефтью? 

Дано:
$m_1 = m_2 = m$
$rho_1 = 13.6 frac{г}{см^3}$
$rho_2 = 0.8 frac{г}{см^3}$

$frac{V_2}{V_1} — ?$

Показать решение и ответ

Скрыть

Задача №10

На одну чашу весов положили мраморный шарик, на другую — шарик из латуни, втрое меньший по объему. Останутся ли весы в равновесии?

Дано:
$V_2 = frac{V_1}{3}$
$rho_1 = 2700 frac{кг}{м^3}$
$rho_2 = 8500 frac{кг}{м^3}$

$frac{m_2}{m_1} — ?$

Показать решение и ответ

Скрыть

Содержание:

Плотность, единицы плотности:

Мы часто употребляем выражение «легкий, как воздух» или «тяжелый. как свинец». Но знаете ли вы. что воздух внутри, скажем, супермаркета, весит больше 400 кг. а груз такой массы не поднять и силачу. Свинцовое же грузило для удочки легко поднимет даже малыш. Выходит, приведенные выше выражения — неправильные? Подождите делать выводы — давайте разберемся.

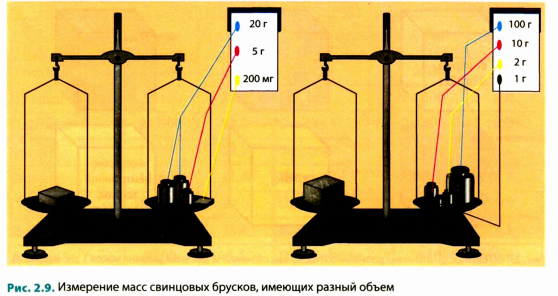
На рис. 2.8 вы видите два бруска, оба бруска изготовлены из одного и того же вещества — свинца, но имеют разные размеры. Наша задача — найти отношение массы каждого бруска к его объему.

Для начала измерьте длину, ширину и высоту брусков и вычислите их объемы. (Если вы правильно выполните измерения и не ошибетесь в расчетах, то вы получите такие результаты: объем меньшего бруска равен 4 см3, большего бруска — 10 см3.)

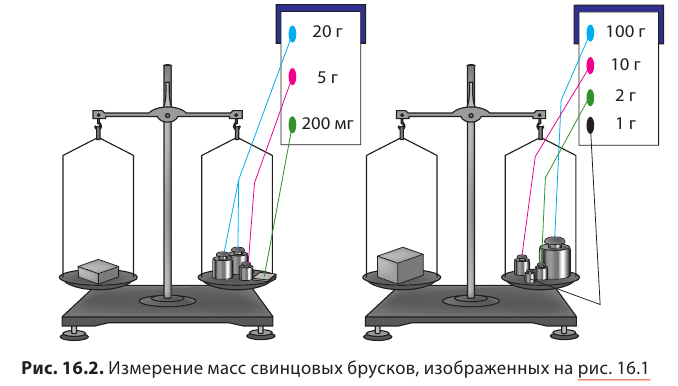
Определив объемы брусков, взвесим их. На левую чашу весов поместим один из брусков, на правую — разновесы (рис. 2.9). Весы находятся в равновесии, ваша задача — сосчитать массу разновесов.

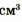
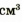
Нам осталось найти отношение массы каждого бруска к его объему, т. е. вычислить, чему равняется масса свинца объемом 1 см3 для меньшего и для большего брусков. Очевидно, что если масса меньшего бруска 45,2 г и он занимает объем 4 , то масса свинца объемом 1 для этого бруска равняется 45,2 : 4 — 11,3 (г). Выполнив аналогичные расчеты для большего бруска, получим 113 : 10 = 11,3 (г). Таким образом, отношение массы свинцового бруска к его объему (масса свинца единичного объема) одинаково как для большего, так и для меньшего брусков.

Если теперь взять бруски, изготовленные из другого вещества (например алюминия), и повторить те же действия, то отношение массы алюминиевого бруска к его объему также не будет зависеть от размеров бруска. Мы снова получим постоянное число, но уже другое, чем в опыте со свинцом.

Определение плотности вещества

Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.

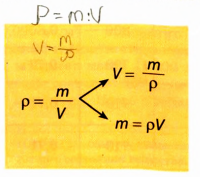
Плотность обозначается символом р и вычисляется по формуле

где V — объем, занятый веществом массой m.

Плотность — это характеристика вещества, не зависящая от массы вещества и его объема. Если увеличить массу вещества, например, в два раза, то объем, который оно займет, также возрастет в два раза*.

Из определения плотности вещества получим единицу плотности. Поскольку в СИ единицей массы является килограмм, а единицей объема — метр кубический, то единицей плотности в СИ будет килограмм на метр кубический (кг/м*).

1 кг/м-* — это плотность такого однородного вещества, масса которого в объеме один кубический метр равняется одному килограмму.

На практике также очень часто применяется единица плотности грамм на сантиметр кубический (г/см*).

Единицы плотности килограмм на метр кубический (кг/м-1) и грамм на сантиметр кубический (г/см3) связаны между собой соотношением:

 

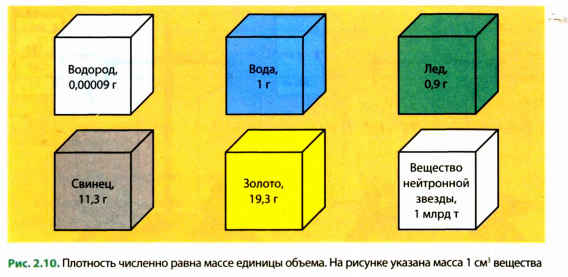
Плотности разных веществ

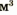
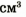
Плотности разных веществ и материалов могут существенно отличаться друг от друга (рис. 2.10). Рассмотрим несколько примеров. Плотность водорода при температуре О С и давлении 760 мм рт. ст. составляет 0,090 кг/ — это значит, что масса водорода объемом 1 равна 0,090 кг, или 90 г. Плотность свинца 11 300 кг/м3. Это означает, что свинец объемом

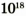
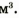
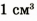
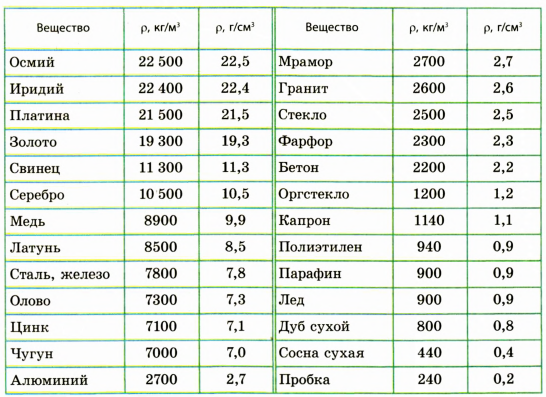
1    м3 имеет массу 11 300 кг, или 11,3 т. Плотность вещества нейтронной звезды достигает кг/. Масса такого вещества объемом равняется 1 млрд тонн. Ниже в таблице приведены плотности некоторых веществ.

Плотность, однако, существенно изменяется в случае изменения температуры и агрегатного состояния вещества. С причинами изменения плотности вещества мы познакомимся далее.

Таблица плотностей некоторых веществ в твердом состоянии

Таблица плотностей некоторых веществ в жидком состоянии

Таблица плотностей некоторых веществ в газообразном состоянии (при температуре О °С и давлении 760 мм рт. ст.)

Вычисление плотности, массы и объема физического тела

На практике часто бывает необходимо определить, из какого вещества состоит то или иное физическое тело. Для этого можно воспользоваться таким способом. Вначале вычислить плотность этого тела, т. е. найти отношение массы тела к его объему. Далее, воспользовавшись данными таблицы плотностей, выяснить, какому веществу соответствует найденное значение плотности.

Например, если глыба объемом 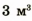имеет массу 2700 кг, то очевидно, что плотность глыбы равна:

По таблице находим, что глыба состоит из льда.

В приведенных выше примерах мы рассматривали так называемые однородные тела, т. е. тела, не имеющие пустот и состоящие из одного ее щества (ледяная глыба, свинцовый и алюминиевый бруски). В таких случаях плотность тела равна плотности вещества, из которого оно состоит (плотность ледяной глыбы = плотности льда).

Если в теле есть пустоты или оно изготовлено из различных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела, которая также исчисляется по формуле

где V — объем тела массой m.
Средняя плотность тела человека, например, составляет

Зная плотность вещества, из которого изготовлено тело (или среднюю плотность тела), и объем тела, можно определить массу данного тела без взвешивания. В самом деле, если

Соответственно, зная плотность и массу тела, можно найти его объем:

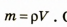
Итоги:
Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.

Плотность вещества и плотность тела можно рассчитать по формуле

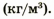
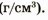
В СИ плотность измеряется в килограммах на метр кубический Часто также используют единицу плотности грамм на сантиметр кубический. Эти единицы связаны между собой соотношением:

Зная массу тела и его плотность, можно найти объем тела: 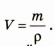Соответственно, по известным объему тела и его плотности можно найти массу тела:

Плотность и единицы плотности

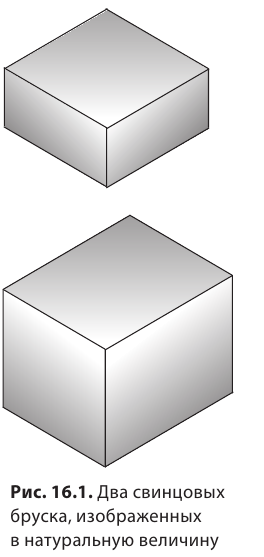
Вы наверняка слышали выражения «легкий, как воздух», «тяжелый, как свинец». При этом воздух внутри, скажем, супермаркета имеет массу более 5000 кг! Поднять груз такой массы не сможет и силач. В то же время свинцовое грузило для удочки легко поднимет даже малыш. Так что же, приведенные выражения ошибочны? Выясним, в чем здесь дело.

На рис. 16.1 изображены два однородных (не имеющих пустот) свинцовых бруска разного объема. Массы брусков тоже разные. Наша задача — найти отношение массы каждого бруска к его объему, то есть определить массу свинца объемом

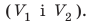
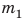
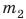
1)Измерьте длину, ширину, высоту брусков и вычислите их объемы 2)Определите массу каждого бруска ( и ) (рис. 16.2). Весы находятся в равновесии, значит, следует найти массу разновесов.

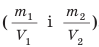
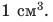
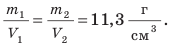
3)Определите отношение массы каждого бруска к его объему , то есть узнайте, какова в каждом случае масса свинца объемом Надеемся, что вы все сделали правильно и для обоих брусков получили одинаковые результаты: Итак, мы определили, что масса свинца объемом равна 11,3 г.

Как вы считаете, изменится ли результат, если для эксперимента взять однородные свинцовые бруски вдвое большей массы? Если изменится, то как?

Определение плотности вещества

Мы провели измерения и расчеты для тел, изготовленных из свинца. Если для эксперимента взять однородные тела, изготовленные из другого вещества, например алюминия, то снова получим одинаковые результаты, но уже другие, чем в опыте со свинцом.

Отношение массы тела к его объему — характеристика не тела, а вещества, из которого это тело изготовлено. Эту величину называют плотность вещества.

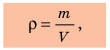
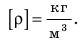
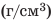
Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела: где ρ («ро») — плотность вещества; m — масса тела; V — объем тела (объем, занятый веществом). В СИ единица массы — килограмм, единица объема — метр кубический, поэтому единица плотности в СИ — килограмм на метр кубический: Используют также единицу плотности грамм на сантиметр кубический . Единицы плотности килограмм на метр кубический и грамм на сантиметр кубический связаны соотношением:

Сравнение плотности разных веществ

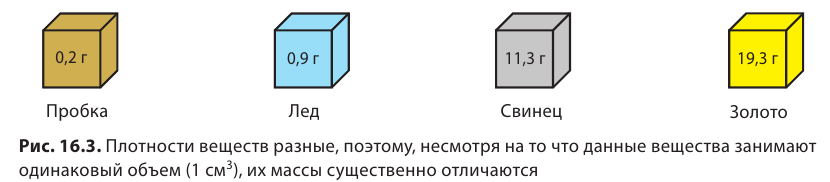
Плотности веществ могут существенно отличаться. Именно поэтому одинаковые по размерам однородные тела, изготовленные из разных веществ, будут иметь разную массу. Приведем несколько примеров.

Кубики на рис. 16.3 изображены в натуральную величину и являются однородными. Объем каждого кубика — , массы кубиков указаны на рисунке.

Первый кубик изготовлен из пробки. Плотность пробки составляет — это означает, что масса пробки объемом равна 0,2 г. Плотность льда , следовательно, масса льда объемом равна 0,9 г. Плотность свинца составляет , поэтому однородное свинцовое тело объемом имеет массу 11,3 г. Используя рис. 16.3, найдите плотность золота. По таблицам плотностей некоторых веществ (см. с. 249 учебника) определите массу кубика объемом , изготовленного из латуни.

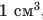
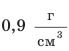
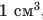
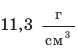
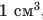
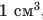
От чего зависит плотность вещества

Плотность существенно зависит от агрегатного состояния и температуры вещества. Если вещество изменяет свое агрегатное состояние или температуру, его масса остается неизменной, так как количество частиц (молекул, атомов) и масса каждой из них не изменяются. А вот объем вещества изменяется, поскольку изменяется среднее расстояние между частицами. Так, при переходе вещества из жидкого состояния в газообразное плотность вещества уменьшается, поскольку увеличивается среднее расстояние между частицами, а значит, увеличивается объем, который занимает вещество (рис. 16.4).

С увеличением температуры среднее расстояние между частицами увеличивается, соответственно увеличивается объем вещества и уменьшается его плотность. И наоборот, чем ниже температура вещества, тем меньше межмолекулярные промежутки, а значит, меньше объем вещества и больше — его плотность*. 5

Вычисление и расчёт плотности тела, массы и объем тела

Как выяснить, из какого вещества изготовлено однородное тело? Один из способов — определить плотность этого тела и сравнить полученный результат с данными таблиц плотностей. Чтобы определить плотность тела, достаточно измерить его массу и объем и вычислить отношение массы тела к его объему.

Исключениями являются вода, чугун и некоторые другие вещества. Например, при нагревании воды от О °C до 4 °C ее плотность увеличивается. Плотность — это характеристика вещества, но иногда, например для сокращения записи, употребляют термин «плотность тела».

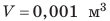
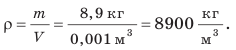
Например, если однородная фигурка объемом имеет массу m = 8,9 кг, то плотность вещества, из которого она изготовлена, равна: По таблице плотностей определяем, что фигурка изготовлена из вещества, имеющего такую же плотность, что и медь (рис. 16.5).

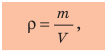
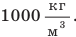
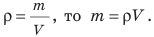
До сих пор речь шла об однородных телах, то есть телах, не имеющих пустот и состоящих из одного вещества (свинцовые бруски, медная фигурка). А вот если в теле есть пустоты или оно состоит из разных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела; ее вычисляют по формуле: где ρ— средняя плотность тела; V — объем тела; m — масса тела. Так, средняя плотность тела человека чуть больше Зная объем тела и его плотность (плотность вещества, из которого оно изготовлено, или среднюю плотность тела), можно определить массу тела без взвешивания. Действительно, если Соответственно, зная массу тела и его плотность, можно найти объем тела:

Итоги:

Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела. Плотность можно определить по формуле

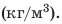
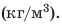
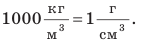
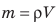
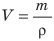
Единица плотности в СИ — килограмм на метр кубический Также используют единицу плотности грамм на сантиметр кубический Эти единицы связаны соотношением: Зная объем тела и его среднюю плотность, можно найти массу тела: . По известным массе и плотности можно найти объем тела: .

Напомним: приступив к решению задачи по физике, сначала следует несколько раз внимательно прочитать ее условие и понять, какое явление описано в задаче, какое тело рассматривается. Другими словами, нужно четко представить ситуацию, которую описывает задача, а уже потом приступать к поиску ответа. Итак, внимательно читаем, думаем, решаем. Попробуйте сначала поработать над каждой задачей самостоятельно, а уже потом ознакомьтесь с ее решением в учебнике.

• Заказать решение задач по физике

Пример №1

Однородный кубик с ребром 2 см имеет массу 20 г. Из какого вещества изготовлен кубик? Анализ физической проблемы. Для ответа на вопрос определим плотность вещества, из которого изготовлен кубик, а потом воспользуемся таблицей плотностей. Задачу будем решать в единицах, данных в условии.

Дано:

,.

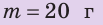
Найти:

Решение:

По определению плотности:

Объем куба вычисляют по формуле:

Следовательно, имеем:

Проверим единицу, найдем значение искомой величины:

Анализ результата. Из таблицы плотностей узнаем, что плотность 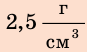имеет стекло.

Ответ: кубик, возможно, изготовлен из стекла.

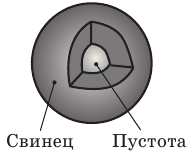
Пример №2

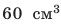
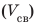
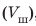
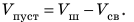
Свинцовый шар объемом имеет массу 0,565 кг. Определите, однородный этот шар или имеет пустоту. Если в шаре есть пустота, вычислите ее объем. Анализ физической проблемы. Выполним пояснительный рисунок. Если объем свинца меньше объема шара , то шар имеет пустоту, объем которой равен: Определяя объем свинца, будем считать, что масса свинца равна массе шара:

Плотность свинца найдем в таблице плотностей. В данной задаче массу лучше выразить в граммах, объем — в сантиметрах кубических, плотность — в граммах на сантиметр кубический.

Дано:

,,,

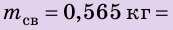
Найти:

Решение:

1. Определим объем свинца.

По определению плотности: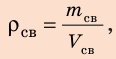поэтому

Проверим единицу, найдем значение искомой величины:

Анализ результатов: 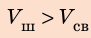, следовательно, шар имеет пустоту.

2. Вычислим объем пустоты:

Ответ:

Пример №3

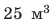
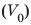
Сколько железнодорожных цистерн емкостью каждая требуется для перевозки 1080 т нефти? Анализ физической проблемы. Количество цистерн можно найти, разделив общий объем нефти (V) на емкость одной цистерны . Общий объем нефти определим по ее массе и плотности. Плотность нефти найдем в таблице плотностей. Задачу будем решать в единицах СИ.

Дано:

,,

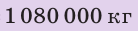
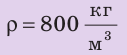
Найти:

Решение:

Из определения плотности найдем общий объем нефти:

Определим общее количество цистерн:

Проверим единицу, найдем значение искомой величины:

Анализ результатов. Количество цистерн, полученное в результате расчетов, вполне реально.

Ответ: N=54.

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.