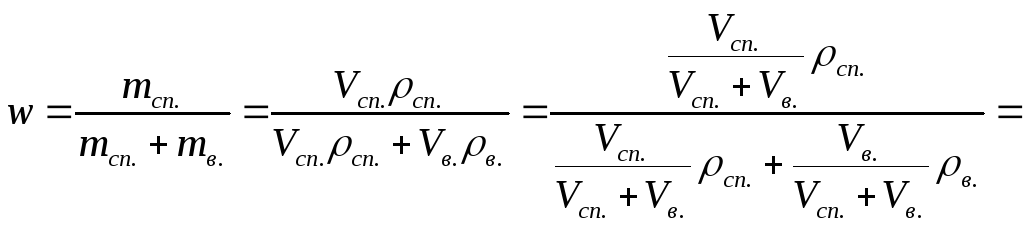Как найти плотность смеси
Смесь состоит минимум из двух компонентов, перемешанных в хаотичном порядке без определенной системы. Каждый из них имеет свою плотность. Для определения плотности смеси нужно знать массы или объемы веществ, которые смешиваются. Плотность жидких смесей измеряется ареометром.

Вам понадобится
- — ареометр;
- — таблица плотностей веществ;
- — весы;
- — мерный цилиндр.
Инструкция
Для измерения плотности жидкой смеси возьмите ареометр. Погрузите его в жидкость, чтобы он свободно плавал в ней. В верхней части ареометра находится шкала. Определите плотность смеси, совмещая шкалу с нижним краем мениска жидкости, в которую он погружен.
Для расчета плотности смеси взвесьте ее на весах. Значение массы m получите в граммах. С помощью мерного цилиндра, или другим способом, определите объем взвешенного количества смеси V. Измерение произведите в см³. Рассчитайте плотность смеси, поделив ее массу на объем, ρ=m/V. Результат получите в г/см³. Чтобы перевести его в кг/м³, результат умножьте на 1000.
ПримерПри переплавке двух металлов получили 400 г сплава, объемом 50 см³. Определите его плотность. Рассчитайте значение плотности по формуле ρ=400/50=8 г/ см³ или 8000 кг/м³.
Если известны плотности веществ, которые будут смешиваться, и их объемы, как это часто встречается при смешивании жидкостей, рассчитайте плотность получившейся смеси. Измерьте объем смеси. Он может несколько отличаться от суммарного объема смешиваемых жидкостей. Например, при смешивании 1 литра спирта и 1 литра воды объем смеси окажется меньше 2-х литров. Это связанно с особенностями строения молекул этих двух жидкостей.
Если плотности смешиваемых жидкостей неизвестны, найдите их значение в специальной таблице. Для расчета найдите сумму произведений плотности каждой из жидкостей на ее объем ρ1∙V1+ ρ2∙V2+ ρ3∙V3+… и т.д. Полученное значение поделите на общий объем смеси V, ρ=(ρ1∙V1+ ρ2∙V2+ ρ3∙V3+…)/V.
ПримерПри смешивании 1 л воды и 1 л этилового спирта получили 1,9 л смеси. Определите ее плотность. Плотность воды равна 1 г/ см³, спирта — 0,8 г/см³. Переведите единицы объема: 1 л=1000 см³, 1,9=1900 см³. Рассчитайте плотность смеси по формуле для двух компонентов ρ=(ρ1∙V1+ ρ2∙V2)/V=(1∙1000+ 0,8∙1000)/1900≈0,947 г/см³.
Источники:
- Изменение объёма при нагревании
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Точное значение, рассчитанное по вашей формуле: = (2*0,8 + 5*0,9) / 7 = 0,8714
Возьмем первой жидкости 200 г, ее объем будет равен 200/0,8=250мл
Второй жидкости —————-500 г, ее объем будет равен 500/0,9=555,56 мл
При отсутствии особых разниц межмолекулярных взаимодействий в жидкостях,
суммарный объем смеси должен быть равен сумме объёмов, т.е. 250+555,56=805,56 мл
Тогда плотность смеси должна составить 700/805,56=0,8690 г/мл
Такое различие (0,8714 =/= 0,8690) показывает, что ваша формула строго говоря неверна,
и годится лишь для приближенных расчетов.
А если еще учесть, что объёмные эффекты могут быть обусловлены
и различной упаковкой молекул в растворах,
то отличие посчитанной плотности от реальной могут быть и выше
Возрастает различие и при большем дисбалансе в исходных плотностях.
Так, если плотность тяжелой жидкости 3 г/мл (жидкий бром разбавляем гексаном), то имеем (2,37 =/= 1,68)
Изменено 6 Августа, 2020 в 03:59 пользователем M_GM
Способы выражения состава.
|
Способ |
Обозначение содержания компонента |
Международные обозначения |
||
|
Название |
Значение |
в |
в |
|
|
Молярная |
|
x |
y |
х, у |
|
Массовая |
|
|
|
w |
|
Относительная молярная |
|
X |
Y |
X, Y |
|
Относительная массовая |
|
|
|
W |
|
Молярная концентрация |
|
Cx |
Cy |
c |
|
Массовая концентрация |
|
|
|
|
|
Объёмная |
|
xV |
y |
φ |
Примечание:
объёмная доля для газов равна молярной
доле и обозначается y;
объёмная доля для жидкостей обозначается
также как и молярная доля х,
но, поскольку для жидкостей это разные
величины, в скобках делается пометка,
например х
= 10% (об.).
Допускается также использование нижнего
индекса хv.
Расчёт плотности и вязкости.
Плотность газа при температуре Т
(К) и давлении р:
,
где.
Здесь Т0 = 273 К,р0
= 760 ммHg= 1,013·105Па,Vm
= 22,4 м3/кмоль.
Плотность смеси газов:
.
Плотность смеси жидкостей:
;
формула плохо применима к смесям
жидкостей со значительным объёмным
эффектом смешения, таким как вода–этанол.
Плотность суспензий:
.
Вязкость газа при температуре Т
(К):
,
где С– постоянная Сатерленда [1,
табл.V].
Вязкость смеси газов:
.
Для коксового, генераторного и подобных
им газов:

где Ткр i– критическая температураi-го
компонента, К [1, табл.XI].
Вязкость смеси жидкостей
через молярные доли:
;
через объёмные доли:
.
Вязкость суспензий:
при
;
при
.
Семинар 2.
Задача 1.
Определить объём воды и 96%-го (объёмные
%) раствора этанола необходимые для
получения 1 м340%-го раствора
этанола. Температуру жидкостей принять
равной 20°С.
|
Дано: φн= 96% (об.), φк= 40% (об.),
V40% = t= 20°C. |
Найти: Vв |
Схема аппарата: |
Решение.
В зависимости от способа приготовление
растворов объёмные доли могут быть
рассчитаны по двум различным формулам:
(1) и
(2)
Вторая формула применима к растворам,
приготовленным в лабораторных условиях,
когда определённый объём спирта
помещается в мерный цилиндр, а затем
объём доводится дистиллированной водой
до метки.
В промышленности, где имеют дело с
большими объёмами, применима первая
формула, которую мы и будем использовать
в дальнейших расчётах.
Выведем формулу для пересчёта объёмных
долей в массовые:

Аналогично могут быть получены формулы
для пересчёта массовых долей в молярные
и молярных долей в массовые, соответственно:
(4),
(5).
Таблица пересчёта одних концентраций
в другие приведена в [1, с. 283, табл. 6.2], в
начале главы 6 «Основы массопередачи.
Абсорбция».
По формуле (3) производим пересчёт
объёмных долей в массовые для 40%-го и
96%-го растворов:
,
.
Исходя из ближайших табличных значений
плотностей водных растворов этанола,
найдём плотности наших растворов методом
линейной интерполяции:
|
Плотности |
|
|
Масс. % |
Плотность, |
|
100 |
789 |
|
80 |
843 |
|
60 |
891 |
|
40 |
935 |
|
20 |
969 |
|
0 |
998 |
|
|
|
Из подобия большого и малого
(заштрихованного) треугольников получаем
соотношения:
;
.
Следовательно, плотности 40 и 96%-ного
растворов соответственно равны:
,
.
Рассчитаем массу 40%-го раствора этанола:
.
Рассчитаем массу этанола, содержащегося
в растворе:
.
Рассчитаем массовый расход 96%-го раствора
этанола:
.
Рассчитаем массу воды, необходимой для
разбавления 96%-го раствора:
.
Рассчитаем объём 96%-го раствора этанола:
.
Рассчитаем объём воды, необходимой для
разбавления 96%-го раствора:
.
Рассчитаем объёмный эффект смешения:

Задача 2.
При синтезе аммиака из водорода и азота
на выходе из реактора получают смесь,
содержащую 12% (об.) аммиака, 22% (об.) азота
и 66% (об.) водорода. Температура смеси
500°С, давление 30 МПа. Определить
плотности компонентов и плотность
смеси.
Решение
задач на нахождение плотности смесей и сплавов,
средней
плотности неоднородных тел (7 класс)
Ларионов Вадим Сергеевич,
учитель физики МБОУ Лицея №
15 г.Сарова, larionvadim@yandex.ru
Ларионова Наталья Валентиновна,
к.п.н., учитель физики МБОУ Лицея № 15
г.Сарова, nvlarionova@yandex.ru
В статье сформулированы методические рекомендации по
организации факультативного занятия по решению задач на нахождение плотности
смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме,
структурированные по уровню сложности.
Задачи на
нахождение плотности смеси или сплава, средней плотности неоднородного
(«составного») тела являются базовыми при изучении темы «Плотность» и
достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно
поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие,
структура которого соответствует принципу «от простого к сложному» и содержит последовательные
блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см.
приложение).
Средняя плотность
неоднородного («составного») тела, плотность смеси или сплава рассчитывается по
формуле
где m1, m2, m3… -массы отдельных частей тела
(компонентов смеси или сплава), а V1, V2, V3 … — их объёмы.
Для решения задач
по данной теме, необходимо составить систему уравнений, в основе которой лежат
следующие положения:
1. Определительная формула
плотности
2. Свойство аддитивности массы
(масса смеси или сплава равна сумме масс его составных частей)
m=m1+ m2+ m3+…
3. Как правило, в таких задачах
полагают, что объём сплава (смеси) равен сумме объёмов его составных частей
V=V1+V2+V3 …
В задачах, предложенных ниже,
исключением является задача № 6 из блока олимпиадных задач (задача о смешивании
спирта и воды).
Ключевые задачи,
представленные в занятии, в зависимости от подготовки учащихся могут быть
решены непосредственно на уроке при изучении темы «Плотность». В этом случае на
факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам
предлагаются задачи для самостоятельного решения, которые, как правило,
составляют домашнее задание. В этом случае удобно дифференцировать домашнее
задание учеников, предложив не более трёх обязательных задач в зависимости от
уровня подготовленности учеников. Учитель может дополнить списки олимпиадных
задач и задач для самостоятельного решения, используя материалы последних
олимпиад.
Приложение
Плотность смесей, сплавов, «составных» тел
Цель: Научиться решать задачи
на нахождение плотности смесей и сплавов, а также средней плотности
неоднородных тел («составных») тел.
Ключевые задачи
1. Какова плотность сплава из
300г олова и 100г свинца? (8г/см3)
2.
Сплав
изготовлен из меди объёмом 0,4 м3 и цинка массой 710 кг. Какова
плотность сплава? (8540 кг/м3)
3. Для приготовления вишнёвого
сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали.
Какова плотность сиропа, если плотность варенья 1300 кг/м3? (1100
кг/м3)
4. Какова плотность смеси из
глицерина и спирта, если объём спирта составляет половину объёма смеси? Как
изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг/м3, 980 кг/м3)
Олимпиадные задачи
1. Масса первого изделия в 2
раза больше массы второго изделия, а их объёмы находятся в отношении V1:V2=1:3. Плотность первого изделия ρ1=4г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить?
Массой и объёмом клея пренебречь. (1,5 г/см3)
2. Изделие, склеенное из трёх
различных частей, имеет объём V=600см3.
Объёмы частей находятся в соотношении V1:V2:V3=2:3:5, а их плотности – в соотношении ρ1:ρ2:ρ3=4:3:1.
Чему равна масса изделия, если плотность первой части ρ1=2000кг/м3?
(660 г)
3. Ученик измерил плотность
деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м3. Но на
самом деле брусок состоит из двух частей, равных по массе, плотность одной из
которых в два раза больше плотности другой. Найдите плотности обеих частей
бруска. Массой краски можно пренебречь. (450 кг/м3, 900 кг/м3)
4. В дистиллированную воду
аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρр=1200
кг/м3 и массу m=120г. Объём раствора равен
сумме объёмов воды и кислоты. Плотность воды ρв=1000 кг/м3,
плотность кислоты ρк=1800 кг/м3. Какова масса кислоты,
влитой в воду? (45 г)
5. 
a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали
форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ,
в результате чего получился куб со стороной 3a (см. рисунок). Определите
среднюю плотность получившейся системы. (67ρ/27≈2,5ρ)
6. Плотностью вещества называют
отношение массы тела из этого вещества к его объёму. Например, масса 1 см3
воды составляет 1 г, поэтому плотность воды 1 г/см3. Представим, что
смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см3, и
при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова
плотность полученного раствора? (ρ=18/19 г/cм3≈0,95г/cм3)
Задачи
для самостоятельного решения
1. Какую плотность имеет сплав
из 270г алюминия и 445г меди? (≈4,77
г/cм3)
2. Сплав золота и серебра массой
400 г имеет плотность 1,4·104 кг/м3. Полагая объём сплава
равным сумме объёмов его составных частей, определите массу золота в сплаве? (220
г)
3. Масса первого изделия в 3
раза меньше массы второго изделия, а их объёмы находятся в соотношении V1:V2=2:1. Плотность первого тела ρ1=1,8 г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой
и объёмом клея пренебречь. (4,8 г/см3)
4. Изделие, склеенное из трёх
различных частей, имеет объём V=900см3.
Объёмы частей находятся в соотношении V1:V2:V3=5:3:1, а их плотности – в соотношении ρ1:ρ2:ρ3=1:2:5.
Чему равна масса изделия, если плотность первой части ρ1=500кг/м3?
(800 г)
5. Кубик с ребром a=20см сделан из материала с
плотностью ρ=3000кг/м3. Однако внутри кубика имеется воздушная
полость, поэтому его средняя плотность ρср=1200кг/м3.
Определите объём этой воздушной полости. Во сколько раз изменится средняя
плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри
полости можно пренебречь. (4800 см3, 1,5)
Литература к занятию
1. Генденштейн Л.Э., Кирик Л.А.,
Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова.
– М.: Илекса, 2009. – 416 с.
2. Бажанский И.И., Гой В.А.,
Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное
пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.
3. Олимпиады 2008-2009. Физика.
Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.:
МЦНМО, 2009. – 70 с.
4. 400 физических этюдов.
Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.
5.
Борисов
С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009. –
100 с.
Ключевые ситуации при изучении физики. Сплавы
Наибольшие трудности при изучении физики учащиеся испытывают при решении задач, т.е. когда требуется применить знания. Эти трудности представляются ребятам настолько большими, что многие из них отказываются даже от попыток решать задачи. Отказ от решения задач еще как-то «проходил» во времена устных экзаменов по физике. Но теперь – как при прохождении Государственной итоговой аттестации, выполнении заданий Единого государственного экзамена или тестирования при поступлении – проверяют именно умение применять полученные знания, а не декларировать их.
Понимание смысла физических законов – главная цель школьного курса физики, но понимание этих законов может родиться только в осознанной деятельности по применению этих законов. Школьникам же часто предлагают алгоритмы решения задач, которые провоцируют бездумное, автоматическое применение физических формул.
Преодолеть эту принципиальную трудность можно, только неоднократно применяя законы физики в тщательно отобранных простейших ситуациях, когда смысл этих законов кристально ясен.
В школьном курсе физики тысячи задач. Однако, если посмотреть на все множество этих задач «с высоты птичьего полета», то нетрудно заметить, что подавляющее их большинство группируются вокруг нескольких десятков типичных учебных ситуаций. Эти ситуации можно назвать ключевыми. А овладение ключевыми ситуациями «даст ключи» к решению задач.
Ключевые ситуации – важнейшая связь между «теорией» и «задачами». Без этой связи теория мертва для школьника, а задачи представляются ему случайной россыпью неинтересных загадок. Однако пока еще некоторые учителя «дают» своим ученикам «теорию» отдельно, а «задачи» отдельно. После такого разрезания по живому от живой физики остаются только мертвые формулы-шаблоны для примитивных задач на подстановку.
Изучение ключевых ситуаций – это живой мост между «теорией» и «задачами», причем мост с двухсторонним движением. С одной стороны, задачи рождаются при изучении ключевых ситуаций, в которых наглядно проявляется действие физических законов, с другой стороны, благодаря решению задач на основе ключевой ситуации теория осознается, т.е. становится действенной силой, а не пассивным набором фактов и формул.
И еще одна очень важная роль ключевых ситуаций. Дело в том, что результатом изучения школьного курса физики должен быть не набор решенных задач (это быстро забывается), а понимание физических законов и физическая интуиция, которая может развиваться именно при рассмотрении ключевых ситуаций.
Приложение 1. Фрагмент урока с выделением ключевой ситуации по теме «Плотность».
Приложение 2. Фрагмент урока с выделением ключевой ситуации по теме «Полые тела».
Приложение 3. Дополнительный материал по теме «Сплавы».
Приведем фрагмент урока с выделение ключевой ситуации по теме «Сплавы».
Фрагмент урока по теме «СПЛАВЫ»
Учитель. Тема урока зашифрована ребусом. Кто первый раскроет секрет?
Ученики. …
Учитель. Тема урока «Сплавы».
Сплав — макроскопически однородная смесь двух или большего числа химических элементов с преобладанием металлических компонентов. Основной или единственной фазой сплава, как правило, является твёрдый раствор легирующих элементов в металле, являющемся основой сплава.
Сплавы имеют металлические свойства, например: металлический блеск, высокие электропроводность и теплопроводность. Иногда компонентами сплава могут быть не только химические элементы, но и химические соединения, обладающие металлическими свойствами. Например, основными компонентами твёрдых сплавов являются карбиды вольфрама или титана. Макроскопические свойства сплавов всегда отличаются от свойств их компонентов, а макроскопическая однородность многофазных (гетерогенных) сплавов достигается за счёт равномерного распределения примесных фаз в металлической матрице.
Сплавы обычно получают с помощью смешивания компонентов в расплавленном состоянии с последующим охлаждением. При высоких температурах плавления компонентов, сплавы производятся смешиванием порошков металлов с последующим спеканием (так получаются, например, многие вольфрамовые сплавы).
Сплавы являются одним из основных конструкционных материалов. Среди них наибольшее значение имеют сплавы на основе железа и алюминия. В состав многих сплавов могут вводиться и неметаллы, такие как углерод, кремний, бор и др. В технике применяется более 5 тыс. сплавов.
Цель нашего урока – научиться решать задачи для определения плотности, массы или объема сплавов или веществ входящих в их состав.
Рассматривая сплавы, обычно предполагают, что объем сплава равен сумме объемов составляющих его веществ. В таком случае плотность сплава , где индексы 1 и 2 относятся к двум компонентам сплава.
Если заданы или требуется найти массы компонентов известной плотности ρ1 и ρ2, то объемы компонентов надо выразить через их массы и плотности, в результате чего формула для плотности сплава примет вид .
Часто в задаче дано или требуется найти соотношение масс компонентов сплава. Обозначим . Тогда . Эта формула связывает плотность сплава ρ и массовое отношение компонент . Из нее при следует: . Приведенные формулы позволяют по заданному значению одной из величин ( или ρ) найти значение другой.
Запишите в тетрадях:
Примечание.
1. Задача первого уровня предназначена для применения основной формулы: .
2. Задачи второго уровня похожи, поэтому целесообразно применить разные способы решения.
3. Задачи третьего уровня предусмотрены для закрепления способов решения задач предложенных ранее с добавлением дополнительных вычислений (объема и процентного отношения).
РЕШЕНИЕ ЗАДАЧ
Задачи по теме «СПЛАВЫ»:
Найдите плотность бронзы, для изготовления которой взяли 100 г меди и 30 г олова, считая, что объем сплава равен сумме объемов входящих в него металлов.
1. Кусок сплава из свинца и олова массой 664 г имеет плотность 8,3 г/см 3 . Определите массу свинца в сплаве. Принять объем сплава равным сумме объемов его составных частей.
2. В куске кварца содержится небольшой самородок золота. Масса куска 100 г, а его плотность 8 г/см 3 . Определите массу золота, содержащегося в кварце. Принять, что плотность кварца и золота соответственно равны 2,65 и 19,36 г/см 3 .
1. Сплав золота и серебра массой 400 г имеет плотность 14·103 кг/м 3 . Полагая объем сплава равным сумме объемов его составных частей, определите массу, объем золота и процентное содержание его в сплаве.
2. В чистой воде растворена кислота. Масса раствора 240 г, а его плотность 1,2 г/см 3 . Определите объем кислоты в растворе и его процентное содержание, если плотность кислоты 1,8 г/см 3 . Принять объем раствора равным сумме объемов его составных частей.
Выходной контроль:
| 1 | А | соотношение масс |
| 2 | Б | плотность сплава, если известны соотношения масс |
| 3 | В | процентное содержание массы одного из веществ в сплаве |
| 4 | Г | процентное содержание объема одного из веществ в сплаве |
| 5 | Д | плотность сплава |
| 6 | Е | объем кварца |
| 7 | Ж | плотность сплава, при заданных плотностях веществ его составляющих |
Ответы: 1-Д, 2-Ж, 3-А, 4-Б, 5-В. 6-Г, 7-Е.
Домашнее задание:
Сплавы различаются по своему предназначению.
Конструкционные сплавы: стали, чугуны, дюралюминий.
Конструкционные со специальными свойствами (например, искробезопасность, антифрикционные свойства): бронзы, латуни.
Для заливки подшипников: баббит.
Для измерительной и электронагревательной аппаратуры: манганин, нихром.
Для изготовления режущих инструментов: победит.
Подготовьте сообщение о каком-нибудь сплаве. Расскажите о веществах, которые в него входят, о их процентном вхождении в сплав и т.д.
Задачи:
1. Найдите плотность стали (сталь — деформируемый (ковкий) сплав железа с углеродом), для изготовления которой взяли 100 г железа и 2 г углерода (углекислого газа), считая, что объем сплава равен сумме объемов входящих в него веществ.
2. Чтобы получить латунь, сплавили куски меди массой 178 кг и цинка массой 355 кг. Какой плотности была получена латунь? Объем сплава равен сумме объемов его составных частей.
3. Сплав золота и серебра массой 500 г имеет плотность 11 г/см3. Полагая объем сплава равным сумме объемов его составных частей, определите массу, объем золота и процентное содержание его в сплаве.
Ответы: 1. 0,098 г/см 3 , 2. 8540 кг/м 3 , 3. 50 г, 2,59 см 3 , 10%.
Подведение итогов урока. Рефлексия
На полях рабочей тетради изобрази схематически один из рисунков, который соответствует степени усвоения материала на уроке. Солнце – мне все понятно, туча – материал интересный, но надо еще поработать, луна – я все проспал.
Статья «Решение задач на нахождение плотности смесей и сплавов, средней плотности неоднородных тел» (7 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Решение задач на нахождение плотности смесей и сплавов,
средней плотности неоднородных тел (7 класс)
Ларионов Вадим Сергеевич,
учитель физики МБОУ Лицея № 15 г.Сарова, larionvadim @ yandex . ru
Ларионова Наталья Валентиновна,
В статье сформулированы методические рекомендации по организации факультативного занятия по решению задач на нахождение плотности смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме, структурированные по уровню сложности.
Задачи на нахождение плотности смеси или сплава, средней плотности неоднородного («составного») тела являются базовыми при изучении темы «Плотность» и достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие, структура которого соответствует принципу «от простого к сложному» и содержит последовательные блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см. приложение).
Средняя плотность неоднородного («составного») тела, плотность смеси или сплава рассчитывается по формуле
где m 1 , m 2 , m 3 … -массы отдельных частей тела (компонентов смеси или сплава), а V 1 , V 2 , V 3 … — их объёмы.
Для решения задач по данной теме, необходимо составить систему уравнений, в основе которой лежат следующие положения:
1. Определительная формула плотности
2. Свойство аддитивности массы (масса смеси или сплава равна сумме масс его составных частей)
m=m 1 + m 2 + m 3 +…
3. Как правило, в таких задачах полагают, что объём сплава (смеси) равен сумме объёмов его составных частей
V = V 1 + V 2 + V 3 …
В задачах, предложенных ниже, исключением является задача № 6 из блока олимпиадных задач (задача о смешивании спирта и воды).
Ключевые задачи, представленные в занятии, в зависимости от подготовки учащихся могут быть решены непосредственно на уроке при изучении темы «Плотность». В этом случае на факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам предлагаются задачи для самостоятельного решения, которые, как правило, составляют домашнее задание. В этом случае удобно дифференцировать домашнее задание учеников, предложив не более трёх обязательных задач в зависимости от уровня подготовленности учеников. Учитель может дополнить списки олимпиадных задач и задач для самостоятельного решения, используя материалы последних олимпиад.
Плотность смесей, сплавов, «составных» тел
Цель: Научиться решать задачи на нахождение плотности смесей и сплавов, а также средней плотности неоднородных тел («составных») тел.
Ключевые задачи
1. Какова плотность сплава из 300г олова и 100г свинца? (8г / см 3 )
2. Сплав изготовлен из меди объёмом 0,4 м 3 и цинка массой 710 кг. Какова плотность сплава? (8540 кг/м 3 )
3. Для приготовления вишнёвого сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали. Какова плотность сиропа, если плотность варенья 1300 кг/м 3 ? (1100 кг/м 3 )
4. Какова плотность смеси из глицерина и спирта, если объём спирта составляет половину объёма смеси? Как изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг / м 3 , 980 кг / м 3 )
Олимпиадные задачи
1. Масса первого изделия в 2 раза больше массы второго изделия, а их объёмы находятся в отношении V 1 : V 2 =1:3. Плотность первого изделия ρ1=4г/см 3 . Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой и объёмом клея пренебречь. (1,5 г/см 3 )
2. Изделие, склеенное из трёх различных частей, имеет объём V =600см 3 . Объёмы частей находятся в соотношении V 1 : V 2 : V 3 =2:3:5, а их плотности – в соотношении ρ1:ρ2:ρ3=4:3:1. Чему равна масса изделия, если плотность первой части ρ1=2000кг/м 3 ? (660 г)
3. Ученик измерил плотность деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м 3 . Но на самом деле брусок состоит из двух частей, равных по массе, плотность одной из которых в два раза больше плотности другой. Найдите плотности обеих частей бруска. Массой краски можно пренебречь. (450 кг/м 3 , 900 кг/м 3 )
4. В дистиллированную воду аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρр=1200 кг/м 3 и массу m =120г. Объём раствора равен сумме объёмов воды и кислоты. Плотность воды ρв=1000 кг/м 3 , плотность кислоты ρк=1800 кг/м 3 . Какова масса кислоты, влитой в воду? (45 г)
5. 
6. Плотностью вещества называют отношение массы тела из этого вещества к его объёму. Например, масса 1 см 3 воды составляет 1 г, поэтому плотность воды 1 г/см 3 . Представим, что смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см 3 , и при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова плотность полученного раствора? ( ρ =18/19 г/ c м 3 ≈0,95г/ c м 3 )
Задачи для самостоятельного решения
1. Какую плотность имеет сплав из 270г алюминия и 445г меди? (≈ 4,77 г /c м 3 )
2. Сплав золота и серебра массой 400 г имеет плотность 1,4·10 4 кг/м 3 . Полагая объём сплава равным сумме объёмов его составных частей, определите массу золота в сплаве? (220 г)
3. Масса первого изделия в 3 раза меньше массы второго изделия, а их объёмы находятся в соотношении V 1 : V 2 =2:1. Плотность первого тела ρ1=1,8 г/см 3 . Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой и объёмом клея пренебречь. (4,8 г/см 3 )
4. Изделие, склеенное из трёх различных частей, имеет объём V =900см 3 . Объёмы частей находятся в соотношении V 1 : V 2 : V 3 =5:3:1, а их плотности – в соотношении ρ1:ρ2:ρ3=1:2:5. Чему равна масса изделия, если плотность первой части ρ1=500кг/м 3 ? (800 г)
5. Кубик с ребром a =20см сделан из материала с плотностью ρ=3000кг/м 3 . Однако внутри кубика имеется воздушная полость, поэтому его средняя плотность ρср=1200кг/м 3 . Определите объём этой воздушной полости. Во сколько раз изменится средняя плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри полости можно пренебречь. (4800 см 3 , 1,5)
Литература к занятию
1. Генденштейн Л.Э., Кирик Л.А., Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова. – М.: Илекса, 2009. – 416 с.
2. Бажанский И.И., Гой В.А., Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.
3. Олимпиады 2008-2009. Физика. Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.: МЦНМО, 2009. – 70 с.
4. 400 физических этюдов. Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.
5. Борисов С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009. – 100 с.
Подготовка к олимпиадам: 7 класс, плотность
Продолжим подготовку к олимпиадам. Сегодня будем решать задачи на тему “плотность”. При смешивании двух веществ сумма их масс дает массу смеси, а вот с объемами все не так очевидно. Если вы в плотно набитое сухим песком ведро попытаетесь налить воды, то в промежутки между песчинками проникнет достаточное ее количество, таким образом, сумма объемов песка и воды – по-прежнему все то же ведро. О том, что сумма объемов не равна объему смеси, может быть сказано в задаче, или об этом придется догадаться.
Задача 1. Определите плотность сплава, состоящего из $2m$ золота и $7m$ серебра. Плотности металлов известны.
Средняя плотность равна
В данном случае можно считать
Задача 2. Определите плотность сплава, состоящего из $2V$ золота и $7V$ серебра. Плотности металлов известны.
Средняя плотность равна
Объем сплава в данном случае равен сумме объемов компонентов.
Задача 3. Известно, что после того, как из канистры объемом 7 л вылили всю воду, там осталось 1,4 мл воды в виде капель на стенках. Затем канистру плотно закрыли пробкой и поставили на солнце. В результате вся вода внутри канистры испарилась. Определите плотность получившегося газа, если первоначальная плотность воздуха равна 1,3 кг/м$^3$.
Пренебрежем объемом капель по сравнению с объемом канистры. Тогда вначале плотность воздуха равна
Где $m_v$ – масса воздуха.
После того, как капли испарились, плотность можно определить как
Где $m_0$ – масса воды.
Ответ: $rho_2=1,5$ кг/м$^3$.
Задача 4. Однородный кубик со стороной a и плотностью $rho$ поместили внутрь куска глины плотностью $4rho$, которой придали форму куба со стороной $2a$. Получившийся куб облепили пластилином плотностью $2rho$, в результате чего получился куб со стороной $3a$ (см. рисунок). Определите среднюю плотность получившейся системы.
Объем получившегося слепка, очевидно, равен $V=(3a)^3=27a^3$.
Определим массу. Масса внутреннего кубика равна
$$m_1=rho V_1=rho a^3$$
Определим массу глины. Ее объем равен $V_2=(2a)^3-a^3$. Тогда
И, наконец, масса пластилина. Объем его будет равен $(3a)^3-(2a)^2=19a^3$, масса
Тогда плотность всего куска
Задача 5. В ведро, доверху заполненное сухим песком массой 8 кг, добавили 4 л воды. В результате вода вся впиталась и не выступила на поверхность песка. Определите среднюю плотность получившегося сырого песка. Объем ведра 8 литров.
Вот тот случай, когда при смешивании компонентов $Vneq V_1+V_2$.
Плотность будет равна ($m_p$ – масса песка, $m_v$ – масса воды).
Ответ: 1,5 кг/л, или 1500 кг/м$^3$.
Задача 6. Смешали 1 кг воды плотностью 1000 кг/м$^3$ и 2 кг спирта плотностью 800 кг/м$^3$. Известно, что суммарный объем смеси составляет 95% от объема исходных компонент. Определите плотность получившейся смеси.
Тут прямо в условии нам показано, что $Vneq V_1+V_2$.
Плотность будет равна ($m_1$ – масса воды, $m_2$ – масса спирта).
Ответ: 902,25 кг/м$^3$.
Задача 7. В прямоугольном сосуде квадратного сечения (расстояние между стенками сосуда $a = 6$ см) плавает в вертикальном положении тонкостенный стакан квадратного сечения с толстым дном (длина внешней стороны квадрата $b = 4$ см). В пространство между стенками сосуда и стакана тонкой струйкой начинают наливать воду так, что за каждую секунду в сосуд поступает $mu = 2,7$ граммов. С какой скоростью $upsilon$ будет всплывать стакан? Плотность воды ρ=1000 кг/м$^3$.
Сколько воды поступит в стакан за время $Delta t$? $Delta m=mu Delta t$. Она растекается по стакану слоем толщины $h$. Для удобства можно представлять, что вся эта вода располагается у дна. Определим объем этой воды как $Delta V=h a^2$. С другой стороны,
Скорость подъема стакана равна
Задача 8. Однородная деталь из сплава с плотностью 2000 кг/м$^3$ имеет массу $m_1=54$ кг. А её точная копия, но в 3 раза меньших размеров, сделанная из сплава с плотностью 4000 кг/м$^3$, оказалась массой $m_2=2$ кг. Есть подозрение, что внутри копии существует скрытая полость. Какой у неё объём? Ответ дать в см$^3$.
Объем маленькой детали равен $V$, тогда, поскольку большая втрое больше, то ее объем больше в 27 раз – $27V$. Тогда плотность большой детали равна
Следовательно, ее объем равен
Плотность малой детали равна
Где $V_0$ – объем полости.
Задача 9. Для определения качества древесины были экспериментально определены массы досок различной длины. Их ширина равнялась 20 см, толщина 3 см. Зависимость массы досок m от их длины представлена в таблице. Постройте график этой зависимости и по нему найдите массу доски длиной 1 м и плотность древесины.
Строим график и по нему находим массу доски: 4,2 кг.
Для определения плотности возьмем точку не в начале графика, потому что чем больше значение, тем меньше относительная погрешность. Например, точку, где $m=9$ кг. Длина равна тогда (по графику) $L=2,1$. Тогда
Ответ: 4,2 кг, 714,3 кг/м$^3$.
Задача 10. Шарик накачали гелием. Масса газа составляет 20% от массы всего шарика. Через день, когда часть гелия просочилась через стенки, объем шарика уменьшился в 2 раза, а масса гелия стала составлять 10% от массы всего шарика. Определите, во сколько раз изменилась средняя плотность воздушного шарика.
Плотность шарика сначала:
Плотность после того, как он сдулся
Сначала масса складывалась из массы газа и массы оболочки:
После того, как шар сдулся, масса равна
Тогда, возвращаясь к плотностям, имеем:
Тогда отношение плотностей
Задача 11. В ящик с жесткими стенками, имеющий форму куба объемом 1 м в кубе и массой 300 кг, насыпали стальные шары диаметром 20 мм плотностью 7800 кг/м$^3$. Затем ящик потрясли и добавили в него столько шаров, что больше уже не получается засунуть ни одного шара (то есть получилась максимально плотная упаковка шаров в ящике). Суммарная масса шаров и ящика получилась 6072 кг. Далее в этот ящик с шарами досыпали еще мелких шариков диаметром 1 мм, сделанных из того же материала, и снова утрясли ящик до максимально возможного заполнения, досыпая при необходимости мелкие шарики. Оцените, какой после этого стала суммарная масса ящика с шарами и шариками.
Определяем массу шариков «крупного» размера:
Так как они заняли 1м$^3$, то средняя плотность упаковки $rho_=5772$ кг/м$^3$.
Поскольку плотность шариков известна, то определим их объем:
Тогда «свободного» пространства остается $V=1-0,74=0,26$ м$^3$.
Если плотность «упаковки» мелких шариков такая же, как и крупных, то их масса равна
Сложим плотности «крупных» и «мелких» шариков:
Задача 12. Большую коробку доверху заполнили деревянными кубиками, плотно уложив их ровными рядами. Через середины противоположных граней каждого из этих кубиков проделаны по три сквозных квадратных отверстия (схема одного кубика приведена на рисунке). Определите среднюю плотность содержимого коробки, если сторона кубика равна 9 см, а сторона отверстия 3 см. Плотность дерева 800 кг/м3 .
Определим, какую фигуру в итоге вырезали из каждого кубика. Она имеет форму пространственного креста:
Это заключение позволяют сделать размеры кубиков и размер отверстия. Этот «крест» будет состоять из 7 кубиков размером 3 на 3. То есть без отверстий кубик бы состоял из $3^3=27$ кубиков 3 на 3, а с отверстиями он лишился 7 кубиков, поэтому состоит из 20 кубиков 3 на 3. Определим массу 20 маленьких кубиков (то есть массу кубика с дырками):