Теорема пифагора
Определение теоремы пифагора
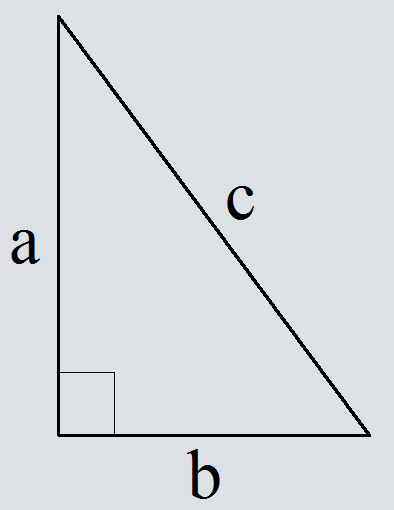
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Обозначив гипотенузу буквой — c, катеты буквами a и b получим следующее равенство
c2=a2+b2
Расчёт катета по теореме пифагора
Введите гипотенузу
c =
Введите катет
b =
Формула пифагора для катета
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Расчёт гипотенузы по теореме пифагора
Введите первый катет
a =
Введите второй катет
b =
Формула пифагора для гипотенузы
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Доказательство теоремы пифагора
Дано
Прямоугольный треугольник с катетами a, b и гипотенузой c.
Доказать
c2=a2+b2
Доказательство
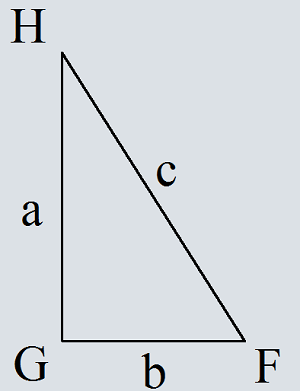
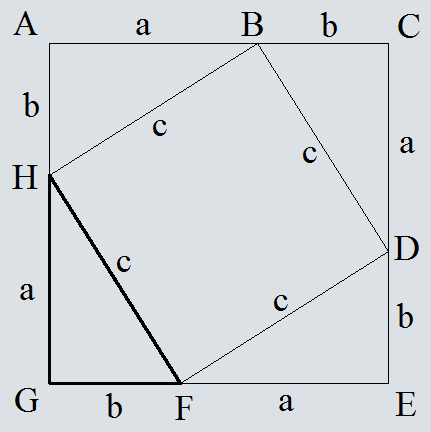
Достроим треугольник HFG до квадрата со стороной a+b.
Запишем площадь получевшегося квадрата двумя способами
S=(a+b)2
S=4*0.5*a*b +c2
Приравняем площади
(a+b)2=4*0.5*a*b +c2
a2+2*a*b +b2=2*a*b +c2
a2+b2=c2
Теорема доказана
Загрузить PDF
Загрузить PDF
Теорема Пифагора связывает три стороны прямоугольного треугольника одной формулой, которой пользуются до сих пор. Теорема гласит, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2, где a и b — катеты треугольника (стороны, пересекающиеся под прямым углом), с — гипотенуза треугольника. Теорема Пифагора применима во многих случаях, например, при помощи этой теоремы легко найти расстояние между двумя точками на координатной плоскости.
-
1
Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
- Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата, а не в виде кривой, которая обозначает непрямые углы.
-
2
Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла).
-
3
Определите, какую сторону треугольника требуется найти. Теорема Пифагора позволяет найти любую сторону прямоугольного треугольника (если известны две другие стороны). Определите, какую сторону (a, b, c) необходимо найти.
- Например, дана гипотенуза, равная 5, и дан катет, равный 3. В этом случае необходимо найти второй катет. Мы вернемся к этому примеру позднее.
- Если две другие стороны неизвестны, необходимо найти длину одной из неизвестных сторон, чтобы иметь возможность применить теорему Пифагора. Для этого используйте основные тригонометрические функции (если вам дано значение одного из непрямых углов).
-
4
Подставьте в формулу a2 + b2 = c2 данные вам значения (или найденные вами значения). Помните, что a и b — это катеты, а с — гипотенуза.
- В нашем примере напишите: 3² + b² = 5².
-
5
Возведите в квадрат каждую известную сторону. Или же оставьте степени — вы можете возвести числа в квадрат позже.
- В нашем примере напишите: 9 + b² = 25.
-
6
Обособьте неизвестную сторону на одной стороне уравнения. Для этого перенесите известные значения на другую сторону уравнения. Если вы находите гипотенузу, то в теореме Пифагора она уже обособлена на одной стороне уравнения (поэтому делать ничего не нужно).
- В нашем примере перенесите 9 на правую сторону уравнения, чтобы обособить неизвестное b². Вы получите b² = 16.
-
7
Извлеките квадратный корень из обеих частей уравнения. На данном этапе на одной стороне уравнения присутствует неизвестное (в квадрате), а на другой стороне — свободный член (число).
- В нашем примере b² = 16. Извлеките квадратный корень из обеих частей уравнения и получите b = 4. Таким образом, второй катет равен 4.
-
8
Используйте теорему Пифагора в повседневной жизни, так как ее можно применять в большом числе практических ситуаций. Для этого научитесь распознавать прямоугольные треугольники в повседневной жизни — в любой ситуации, в которой два предмета (или линии) пересекаются под прямым углом, а третий предмет (или линия) соединяет (по диагонали) верхушки двух первых предметов (или линий), вы можете использовать теорему Пифагора, чтобы найти неизвестную сторону (если две другие стороны известны).
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
- a² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- с = √425
- с = 20,6. Таким образом, приблизительная длина лестницы равна 20,6 метров.
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
Реклама
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
-
1
Выберите две точки на координатной плоскости. По теореме Пифагора можно вычислить длину отрезка, соединяющего две точки на координатной прямой. Для этого необходимо знать координаты (х,у) каждой точки.
- Чтобы найти расстояние между двумя точками, вы будете рассматривать точки в качестве вершин треугольника, не прилежащих к прямому углу прямоугольного треугольника. Таким образом, вы сможете легко найти катеты треугольника, а затем вычислить гипотенузу, которая равна расстоянию между двумя точками.
-
2
Нанесите точки на координатную плоскость. Отложите координаты (х,у), где координата «х» откладывается по горизонтальной оси, а «у» — по вертикальной. Вы можете найти расстояние между точками без построения графика, но график позволяет визуально представить процесс ваших вычислений.
-
3
Найдите катеты треугольника. Вы можете сделать это, измерив длину катетов непосредственно на графике или с помощью формул: |x1 — x2| для вычисления длины горизонтального катета, и |y1 — y2| для вычисления длины вертикального катета, где (x1,y1) – координаты первой точки, а (x2,y2) – координаты второй точки.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
- |x1 — x2|
- |3 — 6|
- | -3 | = 3
- Длины вертикального катета:
- |y1 — y2|
- |1 — 5|
- | -4 | = 4
- Таким образом, в прямоугольном треугольнике а = 3 и b = 4.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
-
4
Используйте теорему Пифагора для нахождения гипотенузы. Расстояние между двумя точками равно гипотенузе треугольника, две стороны которого вы только что нашли. Используйте теорему Пифагора, чтобы найти гипотенузу, подставив в формулу найденные значения катетов (a и b).
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
-
- (3)²+(4)²= c²
- c= √(9+16)
- c= √(25)
- c= 5. Расстояние между точками А(6,1) и В(3,5) равно 5.
-
Реклама
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
Советы
- Гипотенуза всегда:
- лежит напротив прямого угла;
- является самой длинной стороной прямоугольного треугольника;
- обозначается как «с» в теореме Пифагора;
- √(х) означает «квадратный корень из х».
- Не забывайте проверять ответ. Если ответ кажется неправильным, проделайте вычисления снова.
- Еще один момент — самая длинная сторона лежит напротив наибольшего угла, а самая короткая сторона — напротив наименьшего угла.
- Выучите числа пифагоровой тройки, образующие стороны прямоугольного треугольника. Самая примитивная пифагорова тройка — это 3, 4, 5. Так, зная длину двух сторон, третью искать не придется.
- Помните, гипотенуза — всегда самая длинная сторона.
- Если дан обычный треугольник (а не прямоугольный), то требуется больше информации, чем просто длины двух сторон.
- Графики являются наглядным способом нанесения обозначений а, b и с. Если вы решаете задачу, то в первую очередь постройте график.
- Если дана длина только одной стороны, то теорему Пифагора применять нельзя. Попробуйте использовать тригонометрию (sin, cos, tan).
- Если речь идет о задаче из некого сюжета, можно смело предположить, что деревья, столбы, стены и так далее образуют прямой угол с землей, если не указано иное.
Реклама
Об этой статье
Эту страницу просматривали 140 209 раз.
Была ли эта статья полезной?
Содержание:
- Формула теоремы Пифагора
- Доказательство теоремы Пифагора
- Геометрическая формулировка теоремы Пифагора
- Примеры решения задач
- Историческая справка
Формула теоремы Пифагора
Теорема
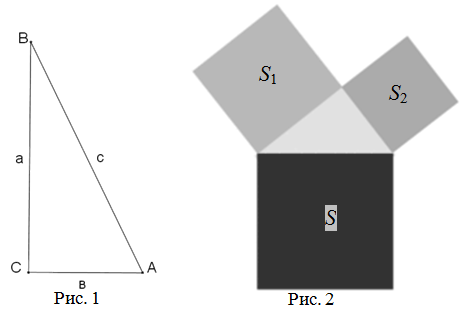
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):
Доказательство теоремы Пифагора
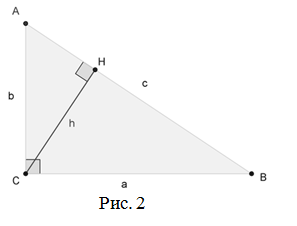
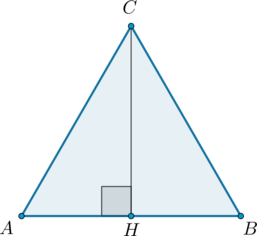
Пусть треугольник $A B C$ — прямоугольный треугольник с
прямым углом $C$ (рис. 2).
Проведём высоту из вершины $C$ на гипотенузу $A B$, основание высоты обозначим как $H$ .
Прямоугольный треугольник $A C H$ подобен треугольнику $A B C$ по двум углам ( $angle A C B=angle C H A=90^{circ}$,
$angle A$ — общий). Аналогично, треугольник $C B H$ подобен $A B C$ .
Введя обозначения
$$B C=a, A C=b, A B=c$$
из подобия треугольников получаем, что
$$frac{a}{c}=frac{H B}{a}, frac{b}{c}=frac{A H}{b}$$
Отсюда имеем, что
$$a^{2}=c cdot H B, b^{2}=c cdot A H$$
Сложив полученные равенства, получаем
$$a^{2}+b^{2}=c cdot H B+c cdot A H$$
$$a^{2}+b^{2}=c cdot(H B+A H)$$
$$a^{2}+b^{2}=c cdot A B$$
$$a^{2}+b^{2}=c cdot c$$
$$a^{2}+b^{2}=c^{2}$$
Что и требовалось доказать.
Геометрическая формулировка теоремы Пифагора
Теорема
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей
квадратов, построенных на катетах (рис. 2):
Примеры решения задач
Пример
Задание. Задан прямоугольный треугольник $A B C$, катеты которого равны 6 см и 8 см.
Найти гипотенузу этого треугольника.
Решение. Согласно условию катеты $a=6$ см, $b=8$ см. Тогда, согласно теореме
Пифагора, квадрат гипотенузы
$c^{2}=a^{2}+b^{2}=6^{2}+8^{2}=36+64=100$
Отсюда получаем, что искомая гипотенуза
$c=sqrt{100}=10$ (см)
Ответ. 10 см

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти
площадь прямоугольного треугольника, если известно, что один
из его катетов на 5 см больше другого, а гипотенуза равна 25 см.
Решение. Пусть
$x$ см — длина меньшего катета, тогда $(x+5)$ см — длина большего. Тогда согласно теореме Пифагора имеем:
$$x^{2}+(x+5)^{2}=25^{2}$$
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:
$x^{2}+5 x-300=0$
Согласно теореме Виета, получаем, что
$x_{1}=15$ (см) , $x_{2}=-20$ (см)
Значение $x_{2}$ не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший — 20 см.
Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть
$$S=frac{15 cdot 20}{2}=15 cdot 10=150left(mathrm{см}^{2}right)$$
Ответ. $S=150left(mathrm{см}^{2}right)$
Историческая справка
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая
соотношение между сторонами прямоугольного треугольника.
В древнекитайской книге «Чжоу би суань цзин» говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий
историк математики Мориц Кантор (1829 — 1920) считает, что равенство $3^{2}+4^{2}=5^{2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является
единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным
значением теоремы для геометрии.
Остались вопросы?
Здесь вы найдете ответы.
Как выглядит формула, отражающая смысл теоремы Пифагора?
Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с
прямыми углами, возведенное в квадратную степень, является величиной,
равной сумме его катетов (а и b), каждый из которых также возведен в
квадрат. Наглядно и с применением условных обозначений это выглядит так:
a² + b² = c².
О чем гласит теорема Пифагора?
В теореме Пифагора говорится о том, что в треугольнике с прямыми углами
сумма длин катетов, каждая из которых возведена в квадрат, равна длине его
гипотенузы, также возведенной в квадратную степень.
При этом под гипотенузой понимается сторона, которая расположена
противоположно прямому углу. Катетом считается одна из сторон, участвующих
в образовании прямого угла.
Треугольник имеет прямой угол. Как доказать теорему Пифагора, которая
гласит, что сумма квадратов катетов прямоугольного труегольника равна длине
его гипотенузы, которая возведена в квадрат?
Основание прямоугольного треугольника обозначим как Н. Из его вершины С
проведем высоту на гипотенузу АВ. Получившийся в результате этого
треугольник АСН является подобным треугольнику АВС по двум углам, равным
90º (∠ACB =∠CHA).
В обоих треугольниках есть один общий угол — ∠A.
Подобными также являются треугольные фигуры АВС и СВН. Основанием их
подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют
общий угол, которым является ∠B.
Для продолжения доказательства теоремы Пифагора следует ввести
дополнительные обозначения: BC = a, AC = b, AB = c.
На основании полученной ранее информации о подобии треугольников можно
утверждать, что:
a/с = HB/a, b/с = AH/b.
Полученное равенство также позволяет сделать следующий вывод:
a2 = c * HB, b2 = c * AH.
На следующем этапе произведем сложение полученных ранее равенств:
a2 + b2 = c * HB + c * AH
Вынесем за скобки общий множитель во второй части равенства:
a2 + b2 = c * (HB + AH)
Теперь можно сократить Н в левой части равенства, в результате получим:
a2 + b2 = c * AB
В приведенных выше обозначениях указано, что АВ = с. Это позволяет
переписать равенство следующим образом:
a2 + b2 = c * c, или a2 + b2 = c2
Таким образом, теорема Пифагора доказана.
Длина катетов прямоугольного треугольника равна 5 см. Как вычислить длину
его гипотенузы?
Согласно теореме Пифагора, длина гипотенузы прямоугольного треугольника,
которая возведена в квадрат, равна сумме, полученной в результате сложения
квадратов длин его катетов. Из этого следует, что:
х² = 5^2 + 5^2
Извлечем квадрат из обеих частей равенства, в итоге получим:
x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2
Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен
5 см, составляет 5√2, что равно примерно 7,07 см.
Применима ли теорема Пифагора к любому треугольнику?
Теорема Пифагора не может быть применима к треугольнику с тупыми или
острыми углами. Она выполняется только в случае прямоугольного
треугольника.
Для треугольника с углом 90º справедливо утверждение о том, что длина его
гипотенузы, возведенная во вторую степень, равна сумме длин его катетов,
взятых в квадрат.
Дан прямоугольный треугольник, длина гипотенузы которого равна 7 см, а
одного катета – 6 см. Как вычислить длину второго катета, используя теорему
Пифагора?
В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного
треугольника, возведенных во вторую степень, равна квадрату длины его
гипотенузы. В случае с треугольником, некоторые параметры которого
приведены в задании, это утверждение выглядит следующим образом:
х² = 7²-6² = 49-36 = 13.
Для того чтобы найти значение х, нужно извлечь квадратный корень из числа
13:
х =√13.
Ответ: Длина второго катета прямоугольного треугольника равна корню
квадратному из 13.
Длина одного из стоящих рядом домов равна 24 м, высота второго из них
составляет 16 м. Как вычислить расстояние между крышами обоих домов, зная,
что квадрат гипотенузы равен сумме квадратов катетов?
Для решения поставленной задачи следует воспользоваться теоремой Пифагора,
которая говорит о том, что сумма длин катетов треугольника с прямым углом,
возведенных в квадрат, равна длине его гипотенузы, также возведенной во
вторую степень:
a² + b² = c².
Теорема Пифагора может быть применима в данном случае по причине того, что
образованная между двумя домами конструкция является прямоугольным
треугольником. Зная о том, что сумма квадратов катетов в прямоугольном
треугольнике равна длине его катета, возведенной в квадрат, можно
вычислить длину неизвестного катета:
24 м – 16 м = 8 м.
Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это,
можно применить теорему Пифагора для вычисления длины гипотенузы:
(16*16) + (8*8) = 256 + 64 = 320 м.
Осталось только извлечь квадратный корень из 320, для того чтобы узнать
длину расстояния между крышами двух домов.
Ответ: Расстояние между крышами домов равно корню квадратному из 320.
Длина гипотенузы треугольника с прямым углом равна 13 см. Один из его
катетов равен 12 см. Как найти длину его второго катета по теореме Пифагора?
Обозначим длину неизвестного катета как х. Зная то, что по теореме
Пифагора длина гипотенузы прямоугольного треугольника, возведенная во
вторую степень, равна сумме длин его катетов, которые также возведены в
квадрат, можно выразить длину неизвестного катета следующим образом:
х² = 132 – 122 = 169 – 144 = 25
Теперь, для того чтобы узнать длину второго катета, необходимо извлечь
квадратный корень из числа 25:
х = √25 = 5
Ответ: длина второго катета прямоугольного треугольника равна 5 см.
Дан треугольник с прямым углом, к гипотенузе которого проведена медиана
длиной 6,5 м. Длина одного из катетов данного треугольника составляет 5 см.
Как вычислить длину второго катета треугольника по теореме Пифагора?
Известно, что длина медианы (m), которая проведена к гипотенузе
прямоугольного треугольника, равна ½ ее длины. Используя это, можно
высчитать длину гипотенузы прямоугольного треугольника:
с = 2*m = 2*6,5 = 13 см.
Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного
треугольника, можно вычислить, чему равен его второй катет. Для этого
можно использовать теорему Пифагора, согласно которой:
a²+b²=c²
В нашем случае:
5²+b²=13²
Выражаем из записанного выше равенства длину неизвестного катета:
b²=13²-5²= 144
Из полученного числа нужно извлечь квадратный корень, для того чтобы
узнать длину второго катета прямоугольного треугольника:
b = √144 = 12 см.
Ответ: Длина второго катета прямоугольного треугольника равна 12 см.
Как можно вычислить треугольник, для которого по теореме Пифагора,
соблюдается равенство f2=a2+ b2?
Равенство, указанное в задании, применимо к треугольнику с прямым углом,
как гласит теорема Пифагора.
Каждая из сторон треугольника может быть обозначена прописной буквой,
которая соответствует строчной букве, обозначающей угол треугольника,
расположенный противоположно этой стороне. На основании этого можно
сделать вывод о том, что искомый треугольник является прямоугольным и
имеет гипотенузу f и катеты a и b:
∆АDF c ∠F= 90°
Ответ: имеется треугольник АDF с прямым углом F.
Существует ли теорема, которая обратна теореме Пифагора, и что она гласит?
Теорема, которая является обратной теореме Пифагора, существует. Согласно
этой теореме, треугольник считается прямоугольным в том случае, если длина
его большей стороны, возведенная в квадратную степень, равна сумме длин
двух других его сторон, которые также возведены в квадратную степень.
Имеется равнобедренный треугольник, длина двух сторон которого равна 48 см,
а третьей – 51 см. Как можно высчитать площадь данного треугольника по
теореме Пифагора?
Для начала следует провести высоту (h) к основанию равнобедренного
треугольника. Данная высота, проведенная к основанию, в случае с
равнобедренным треугольником является медианой.
Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет
равна:
h = √((48 см)² — (25,5 см)²) = 10,5√15 см.
Площадь (S) треугольника рассчитывается путем деления на число, полученное
в результате умножения длины высоты на длину основания треугольника:
S = ½*10,5√15 см*51 см = 267,75√15 см².
Ответ: Площадь треугольника равна 267,75√15 см².
Каким образом можно вычислить высоту равностороннего треугольника со
стороной а по теореме Пифагора?
В равностороннем треугольнике высота (h), проведенная к его основанию,
является также его биссектрисой и медианой. Она делит равносторонний
треугольник на две части, которые являются равными треугольниками с прямым
углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный
вопрос следует применить теорему Пифагора:
h²=a²-(a/2)²=a²-(a²/4)=3a²/4
h=a√3/2.
Дан треугольник с прямым углом, длина одного из катетов которого вдвое
меньше длины его второго катета. Гипотенуза данного треугольника равна корню
квадратному из 15. Как по теореме Пифагора вычислить длину меньшего из
катетов треугольника?
Обозначим меньший из катетов как х. Тогда другой катет, длина которого в
два раза больше, будет обозначен как 2х. Если в случае с прямоугольным
треугольником, длина гипотенузы которого равна √15, применить теорему
Пифагора, то она будет выглядеть следующим образом:
(2х)²+(x)²=√15
После раскрытия скобок в уравнении получаем следующее равенство:
4х²+x²=15
Складываем слагаемые в первой части и получаем:
5x²=15
Сокращаем обе части уравнения на 5, и в итоге получается, что:
x²=3
Это значит, что:
x=√3
Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.
Известно, что длина одного из катетов прямоугольного треугольника составляет
60 см, а длина его гипотенузы и второго катета в сумме дают 180 см. Можно ли
по теореме Пифагора высчитать длину гипотенузы данного треугольника?
Если обозначить длину неизвестного катета через х, то гипотенуза будет
равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для
данного треугольника:
x²+60²=(180-x)² = x²+3600=32400-360x+x²
После сокращений получается следующее равенство:
360х=32400-3600=28800
Теперь можно найти значение х:
х=28800/360=80
Длина второго катета равна 80 см.
Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180
см, можно вычислить длину гипотенузы:
180-80=100 см.
Ответ: Длина гипотенузы равна 100 см.
Дана прямоугольная трапеция ABCD. Ее углы А и В равны по 90°. Длины боковых
сторон данной трапеции составляют 9 см и 18 см. Диагональ АС составляет 15
см. Как можно вычислить длину основания трапеции по теореме Пифагора?
АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см.
Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются
неизвестными величинами. Длину ВС можно вычислить по следующей формуле:
√15²-9²=√144=12 см.
Произведем перенос высоты:
СС1=АВ=9 см.
Тогда получаем, что:
C1D=√18²-9²=9√3
BC=AC1=12
AD=12+9√3 см.
Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.
Потенциал к творчеству обычно приписывают гуманитарным дисциплинам, естественно научным оставляя анализ, практический подход и сухой язык формул и цифр. Математику к гуманитарным предметам никак не отнесешь. Но без творчеств в «царице всех наук» далеко не уедешь – об этом людям известно с давних пор. Со времен Пифагора, например.
Школьные учебники, к сожалению, обычно не объясняют, что в математике важно не только зубрить теоремы, аксиомы и формулы. Важно понимать и чувствовать ее фундаментальные принципы. И при этом попробовать освободить свой ум от штампов и азбучных истин – только в таких условиях рождаются все великие открытия.
К таким открытиям можно отнести и то, которое сегодня мы знаем как теорему Пифагора. С его помощью мы попробуем показать, что математика не только может, но и должна быть увлекательной. И что это приключение подходит не только ботаникам в толстых очках, а всем, кто крепок умом и силен духом.
Из истории вопроса
Строго говоря, хоть теорема и называется «теоремой Пифагора», сам Пифагор ее не открывал. Прямоугольный треугольник и его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал.
Также сегодня известно, что задачи о прямоугольном треугольнике встречаются в египетских источниках времен фараона Аменемхета I, на вавилонских глиняных табличках периода правления царя Хаммурапи, в древнеиндийском трактате «Сульва сутра» и древнекитайском сочинении «Чжоу-би суань цзинь».
Как видите, теорема Пифагора занимала умы математиков с древнейших времен. Подтверждением служит и около 367 разнообразных доказательств, существующих сегодня. В этом с ней не может тягаться ни одна другая теорема. Среди знаменитых авторов доказательств можно вспомнить Леонардо да Винчи и двадцатого президента США Джеймса Гарфилда. Все это говорит о чрезвычайной важности этой теоремы для математики: из нее выводится или так или иначе с нею связано большинство теорем геометрии.
Доказательства теоремы Пифагора
В школьных учебниках в основном приводят алгебраические доказательства. Но суть теоремы в геометрии, так что давайте рассмотрим в первую очередь те доказателства знаменитой теоремы, которые опираются на эту науку.
Доказательство 1
Для самого простого доказательства теоремы Пифагора для прямоугольного треугольника нужно задать идеальные условия: пусть треугольник будет не только прямоугольным, но и равнобедренным. Есть основания полагать, что именно такой треугольник первоначально рассматривали математики древности.
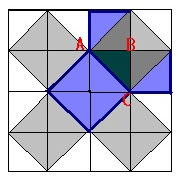
Утверждение «квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» можно проиллюстрировать следующим чертежом:
Посмотрите на равнобедренный прямоугольный треугольник ABC: На гипотенузе АС можно построить квадрат, состоящий из четырех треугольников, равных исходному АВС. А на катетах АВ и ВС построено по квадрату, каждый из которых содержит по два аналогичных треугольника.
Кстати, этот чертеж лег в основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны»:
Доказательство 2
Этот метод сочетает в себе алгебру и геометрию и может рассматриваться как вариант древнеиндийского доказательства математика Бхаскари.
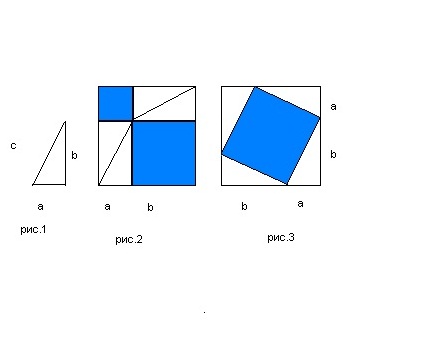
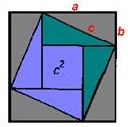
Постройте прямоугольный треугольник со сторонами a, b и c (рис.1). Затем постройте два квадрата со сторонами, равными сумме длин двух катетов, – (a+b). В каждом из квадратов выполните построения, как на рисунках 2 и 3.
В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b.
Во втором квадрате четыре построенных аналогичных треугольника образуют квадрат со стороной, равной гипотенузе c.
Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b).
Записав все это, имеем: a2+b2=(a+b)2 – 2ab. Раскройте скобки, проведите все необходимые алгебраические вычисления и получите, что a2+b2= a2+b2. При этом площадь вписанного на рис.3. квадрата можно вычислить и по традиционной формуле S=c2. Т.е. a2+b2=c2 – вы доказали теорему Пифагора.
Доказательство 3
Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания» («Сиддханта широмани») и в качестве главного аргумента автор использует призыв, обращенный к математическим талантам и наблюдательности учеников и последователей: «Смотри!».
Но мы разберем это доказательство более подробно:
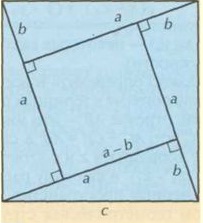
Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на чертеже. Сторону большого квадрата, она же гипотенуза, обозначим с. Катеты треугольника назовем а и b. В соответствии с чертежом сторона внутреннего квадрата это (a-b).
Используйте формулу площади квадрата S=c2, чтобы вычислить площадь внешнего квадрата. И одновременно высчитайте ту же величину, сложив площадь внутреннего квадрата и площади всех четырех прямоугольных треугольников: (a-b)22+4*12*a*b.
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что c2=(a-b)2+4*12*a*b. В результате решения вы получите формулу теоремы Пифагора c2=a2+b2. Теорема доказана.
Доказательство 4
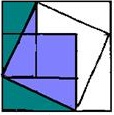
Это любопытное древнекитайское доказательство получило название «Стул невесты» — из-за похожей на стул фигуры, которая получается в результате всех построений:
Рис.1.
Рис. 2.
В нем используется чертеж, который мы уже видели на рис.3 во втором доказательстве. А внутренний квадрат со стороной с построен так же, как в древнеиндийском доказательстве, приведенном выше.
Если мысленно отрезать от чертежа на рис.1 два зеленых прямоугольных треугольника, перенести их к противоположным сторонам квадрата со стороной с и гипотенузами приложить к гипотенузам сиреневых треугольников, получится фигура под названием «стул невесты» (рис.2). Для наглядности можно то же самое проделать с бумажными квадратами и треугольниками. Вы убедитесь, что «стул невесты» образуют два квадрата: маленькие со стороной b и большой со стороной a.
Эти построения позволили древнекитайским математикам и нам вслед за ними прийти к выводу, что c2=a2+b2.
Доказательство 5
Это еще один способ найти решение для теоремы Пифагора, опираясь на геометрию. Называется он «Метод Гарфилда».
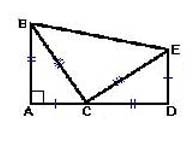
Постройте прямоугольный треугольник АВС. Нам надо доказать, что ВС2=АС2+АВ2.
Для этого продолжите катет АС и постройте отрезок CD, который равен катету АВ. Опустите перпендикулярный AD отрезок ED. Отрезки ED и АС равны. Соедините точки Е и В, а также Е и С и получите чертеж, как на рисунке ниже:
Чтобы доказать терему, мы вновь прибегаем к уже опробованному нами способу: найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трех треугольников, которые ее образуют. Причем один из них, ЕСВ, является не только прямоугольным, но и равнобедренным. Не забываем также, что АВ=CD, АС=ED и ВС=СЕ – это позволит нам упростить запись и не перегружать ее. Итак, SABED=2*1/2(AB*AC)+1/2ВС2.
При этом очевидно, что ABED – это трапеция. Поэтому вычисляем ее площадь по формуле: SABED=(DE+AB)*1/2AD. Для наших вычислений удобней и наглядней представить отрезок AD как сумму отрезков АС и CD.
Запишем оба способа вычислить площадь фигуры, поставив между ними знак равенства: AB*AC+1/2BC2=(DE+AB)*1/2(AC+CD). Используем уже известное нам и описанное выше равенство отрезков, чтобы упростить правую часть записи: AB*AC+1/2BC2=1/2(АВ+АС)2. А теперь раскроем скобки и преобразуем равенство: AB*AC+1/2BC2=1/2АС2+2*1/2(АВ*АС)+1/2АВ2. Закончив все преобразования, получим именно то, что нам и надо: ВС2=АС2+АВ2. Мы доказали теорему.
Конечно, этот список доказательств далеко не полный. Теорему Пифагора также можно доказать с помощью векторов, комплексных чисел, дифференциальный уравнений, стереометрии и т.п. И даже физики: если, например, в аналогичные представленным на чертежах квадратные и треугольные объемы залить жидкость. Переливая жидкость, можно доказать равенство площадей и саму теорему в итоге.
Пару слов о Пифагоровых тройках
Этот вопрос мало или вообще не изучается в школьной программе. А между тем он является очень интересным и имеет большое значение в геометрии. Пифагоровы тройки применяются для решения многих математических задач. Представление о них может пригодиться вам в дальнейшем образовании.
Так что же такое Пифагоровы тройки? Так называют натуральные числа, собранные по трое, сумма квадратов двух из которых равна третьему числу в квадрате.
Пифагоровы тройки могут быть:
- примитивными (все три числа – взаимно простые);
- не примитивными (если каждое число тройки умножить на одно и то же число, получится новая тройка, которая не является примитивной).
Еще до нашей эры древних египтян завораживала мания чисел Пифагоровых троек: в задачах они рассматривали прямоугольный треугольник со сторонами 3,4 и 5 единиц. К слову, любой треугольник, стороны которого равны числам из пифагоровой тройки, по умолчанию является прямоугольным.
Примеры Пифагоровых троек: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) и т.д.
Практическое применение теоремы
Теорема Пифагора находит применение не только в математике, но и в архитектуре и строительстве, астрономии и даже литературе.
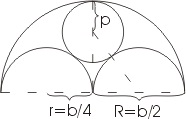
Сначала про строительство: теорема Пифагора находит в нем широкое применение в задачах разного уровня сложности. Например, посмотрите на окно в романском стиле:
Обозначим ширину окна как b, тогда радиус большой полуокружности можно обозначить как R и выразить через b: R=b/2. Радиус меньших полуокружностей также выразим через b: r=b/4. В этой задаче нас интересует радиус внутренней окружности окна (назовем его p).
Теорема Пифагора как раз и пригодиться, чтобы вычислить р. Для этого используем прямоугольный треугольник, который на рисунке обозначен пунктиром. Гипотенуза треугольника состоит из двух радиусов: b/4+p. Один катет представляет собой радиус b/4, другой b/2-p. Используя теорему Пифагора, запишем: (b/4+p)2=(b/4)2+(b/2-p)2. Далее раскроем скобки и получим b2/16+ bp/2+p2=b2/16+b2/4-bp+p2. Преобразуем это выражение в bp/2=b2/4-bp. А затем разделим все члены на b, приведем подобные, чтобы получить 3/2*p=b/4. И в итоге найдем, что p=b/6 – что нам и требовалось.
С помощью теоремы можно вычислить длину стропила для двускатной крыши. Определить, какой высоты вышка мобильной связи нужна, чтобы сигнал достигал определенного населенного пункта. И даже устойчиво установить новогоднюю елку на городской площади. Как видите, эта теорема живет не только на страницах учебников, но и часто бывает полезна в реальной жизни.
Что касается литературы, то теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:
Свет истины рассеется не скоро,
Но, воссияв, рассеется навряд
И, как тысячелетия назад,
Не вызовет сомнения и спора.
Мудрейшие, когда коснется взора
Свет истины, богов благодарят;
И сто быков, заколоты, лежат –
Ответный дар счастливца Пифагора.
С тех пор быки отчаянно ревут:
Навеки всполошило бычье племя
Событие, помянутое тут.
Им кажется: вот-вот настанет время,
И сызнова их в жертву принесут
Какой-нибудь великой теореме.
(перевод Виктора Топорова)
А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый».
А еще в книге «Приключения Электроника» автор устами учителя математики Таратара говорит: «Главное в математике – движение мысли, новые идеи». Именно этот творческий полет мысли порождает теорема Пифагора – не зря у нее столько разнообразных доказательств. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.
Заключение
Эта статья создана, чтобы вы могли заглянуть за пределы школьной программы по математике и узнать не только те доказательства теоремы Пифагора, которые приведены в учебниках «Геометрия 7-9» (Л.С. Атанасян, В.Н. Руденко) и «Геометрия 7-11» (А.В. Погорелов), но и другие любопытные способы доказать знаменитую теорему. А также увидеть примеры, как теорема Пифагора может применяться в обычной жизни.
Во-первых, эта информация позволит вам претендовать на более высокие баллы на уроках математики – сведения по предмету из дополнительных источников всегда высоко оцениваются.
Во-вторых, нам хотелось помочь вам прочувствовать, насколько математика интересная наука. Убедиться на конкретных примерах, что в ней всегда есть место творчеству. Мы надеемся, что теорема Пифагора и эта статья вдохновят вас на самостоятельные поиски и волнующие открытия в математике и других науках.
Расскажите нам в комментариях, показались ли вам приведенные в статье доказательства интересными. Пригодились ли вам эти сведения в учебе. Напишите нам, что думаете о теореме Пифагора и этой статье – нам будет приятно обсудить все это с вами.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Прямоугольный треугольник. Теорема Пифагора
Прямоугольный треугольник – это треугольник, один из углов которого равен (90^circ) (прямой).
Сторона, лежащая напротив прямого угла, называется гипотенузой ((AB)), а две другие стороны — катетами ((AC) и (BC)).
(bullet) Катет, лежащий против угла (30^circ), равен половине гипотенузы.
Следовательно, если, например, (angle A=30^circ), то (BC=dfrac12AB).
(bullet) Сумма острых углов прямоугольного треугольника равна (90^circ): (angle A+angle B=90^circ).
Следовательно, если в прямоугольном треугольнике один из острых углов равен (45^circ), то такой треугольник является равнобедренным.
(bullet) Если в прямоугольном треугольнике (ABC) провести высоту (CH) из прямого угла, то (angle BAC=angle BCH) и (angle
ABC=angle
ACH):
(bullet) Теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов: [AB^2=AC^2+BC^2]
(bullet) (triangle ABCsim triangle AHCsim triangle BHC)
(bullet) Высота, проведенная из вершины прямого угла, есть среднее геометрическое (среднее пропорциональное) отрезков, на которые делится гипотенуза этой высотой: [CH=sqrt{AHcdot HB}]
Задание
1
#3770
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), угол (A) равен (30^circ), (AB=2sqrt3). Найдите высоту (CH).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=sqrt3).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=sqrt3:2).
Тогда по теореме Пифагора из (triangle BCH): [CH=sqrt{BC^2-BH^2}=sqrt{dfrac94}=1,5]
Ответ: 1,5
Задание
2
#3771
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (AH), если (AB=2).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=1).
Тогда по теореме Пифагора из (triangle ABC): [AC=sqrt{AB^2-BC^2}=sqrt3] Из прямоугольного (triangle AHC): (HC=0,5AC=sqrt3:2). Тогда по теореме Пифагора [AH=sqrt{AC^2-HC^2}=1,5]
Ответ: 1,5
Задание
3
#3772
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (BH), если (AB=4).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=2).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=1).
Ответ: 1
Задание
4
#3773
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) ( AB=BC=AC=2sqrt3). Найдите высоту (CH).
Так как (AC=BC), то (CH) также является медианой, следовательно, (AH=0,5 AB=sqrt3). Тогда по теореме Пифагора из (triangle ACH): [CH=sqrt{AC^2-AH^2}=3]
Ответ: 3
Задание
5
#3774
Уровень задания: Равен ЕГЭ
В равностороннем треугольнике (ABC) высота (CH) равна (2sqrt3). Найдите (AB).
Так как (AC=BC), то (CH) также является медианой. Следовательно, если (AH=a), то (AB=AC=2a). Тогда по теореме Пифагора из (triangle
ACH): [AC^2=AH^2+CH^2quadRightarrowquad 4a^2=a^2+12quadRightarrowquad
a=2quadRightarrowquad AB=2a=4]
Ответ: 4
Задание
6
#3775
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC=4), (angle C=30^circ). Найдите высоту (AH).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (AH=0,5AC=2).
Заметим, что условие (BC=4) в данной задаче является лишним.
Ответ: 2
Задание
7
#3776
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC), высота (AH) равна (4), угол (C) равен (30^circ). Найдите (BC).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (4=AH=0,5AC), откуда (8=AC=BC).
Ответ: 8

УСТАЛ? Просто отдохни