Загрузить PDF
Загрузить PDF
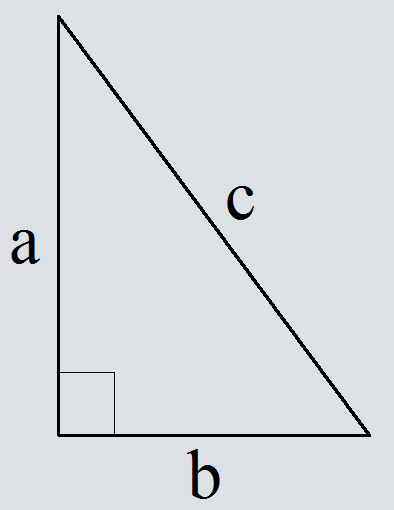
Теорема Пифагора связывает три стороны прямоугольного треугольника одной формулой, которой пользуются до сих пор. Теорема гласит, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2, где a и b — катеты треугольника (стороны, пересекающиеся под прямым углом), с — гипотенуза треугольника. Теорема Пифагора применима во многих случаях, например, при помощи этой теоремы легко найти расстояние между двумя точками на координатной плоскости.
-
1
Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
- Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата, а не в виде кривой, которая обозначает непрямые углы.
-
2
Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла).
-
3
Определите, какую сторону треугольника требуется найти. Теорема Пифагора позволяет найти любую сторону прямоугольного треугольника (если известны две другие стороны). Определите, какую сторону (a, b, c) необходимо найти.
- Например, дана гипотенуза, равная 5, и дан катет, равный 3. В этом случае необходимо найти второй катет. Мы вернемся к этому примеру позднее.
- Если две другие стороны неизвестны, необходимо найти длину одной из неизвестных сторон, чтобы иметь возможность применить теорему Пифагора. Для этого используйте основные тригонометрические функции (если вам дано значение одного из непрямых углов).
-
4
Подставьте в формулу a2 + b2 = c2 данные вам значения (или найденные вами значения). Помните, что a и b — это катеты, а с — гипотенуза.
- В нашем примере напишите: 3² + b² = 5².
-
5
Возведите в квадрат каждую известную сторону. Или же оставьте степени — вы можете возвести числа в квадрат позже.
- В нашем примере напишите: 9 + b² = 25.
-
6
Обособьте неизвестную сторону на одной стороне уравнения. Для этого перенесите известные значения на другую сторону уравнения. Если вы находите гипотенузу, то в теореме Пифагора она уже обособлена на одной стороне уравнения (поэтому делать ничего не нужно).
- В нашем примере перенесите 9 на правую сторону уравнения, чтобы обособить неизвестное b². Вы получите b² = 16.
-
7
Извлеките квадратный корень из обеих частей уравнения. На данном этапе на одной стороне уравнения присутствует неизвестное (в квадрате), а на другой стороне — свободный член (число).
- В нашем примере b² = 16. Извлеките квадратный корень из обеих частей уравнения и получите b = 4. Таким образом, второй катет равен 4.
-
8
Используйте теорему Пифагора в повседневной жизни, так как ее можно применять в большом числе практических ситуаций. Для этого научитесь распознавать прямоугольные треугольники в повседневной жизни — в любой ситуации, в которой два предмета (или линии) пересекаются под прямым углом, а третий предмет (или линия) соединяет (по диагонали) верхушки двух первых предметов (или линий), вы можете использовать теорему Пифагора, чтобы найти неизвестную сторону (если две другие стороны известны).
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
- a² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- с = √425
- с = 20,6. Таким образом, приблизительная длина лестницы равна 20,6 метров.
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
Реклама
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
-
1
Выберите две точки на координатной плоскости. По теореме Пифагора можно вычислить длину отрезка, соединяющего две точки на координатной прямой. Для этого необходимо знать координаты (х,у) каждой точки.
- Чтобы найти расстояние между двумя точками, вы будете рассматривать точки в качестве вершин треугольника, не прилежащих к прямому углу прямоугольного треугольника. Таким образом, вы сможете легко найти катеты треугольника, а затем вычислить гипотенузу, которая равна расстоянию между двумя точками.
-
2
Нанесите точки на координатную плоскость. Отложите координаты (х,у), где координата «х» откладывается по горизонтальной оси, а «у» — по вертикальной. Вы можете найти расстояние между точками без построения графика, но график позволяет визуально представить процесс ваших вычислений.
-
3
Найдите катеты треугольника. Вы можете сделать это, измерив длину катетов непосредственно на графике или с помощью формул: |x1 — x2| для вычисления длины горизонтального катета, и |y1 — y2| для вычисления длины вертикального катета, где (x1,y1) – координаты первой точки, а (x2,y2) – координаты второй точки.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
- |x1 — x2|
- |3 — 6|
- | -3 | = 3
- Длины вертикального катета:
- |y1 — y2|
- |1 — 5|
- | -4 | = 4
- Таким образом, в прямоугольном треугольнике а = 3 и b = 4.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
-
4
Используйте теорему Пифагора для нахождения гипотенузы. Расстояние между двумя точками равно гипотенузе треугольника, две стороны которого вы только что нашли. Используйте теорему Пифагора, чтобы найти гипотенузу, подставив в формулу найденные значения катетов (a и b).
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
-
- (3)²+(4)²= c²
- c= √(9+16)
- c= √(25)
- c= 5. Расстояние между точками А(6,1) и В(3,5) равно 5.
-
Реклама
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
Советы
- Гипотенуза всегда:
- лежит напротив прямого угла;
- является самой длинной стороной прямоугольного треугольника;
- обозначается как «с» в теореме Пифагора;
- √(х) означает «квадратный корень из х».
- Не забывайте проверять ответ. Если ответ кажется неправильным, проделайте вычисления снова.
- Еще один момент — самая длинная сторона лежит напротив наибольшего угла, а самая короткая сторона — напротив наименьшего угла.
- Выучите числа пифагоровой тройки, образующие стороны прямоугольного треугольника. Самая примитивная пифагорова тройка — это 3, 4, 5. Так, зная длину двух сторон, третью искать не придется.
- Помните, гипотенуза — всегда самая длинная сторона.
- Если дан обычный треугольник (а не прямоугольный), то требуется больше информации, чем просто длины двух сторон.
- Графики являются наглядным способом нанесения обозначений а, b и с. Если вы решаете задачу, то в первую очередь постройте график.
- Если дана длина только одной стороны, то теорему Пифагора применять нельзя. Попробуйте использовать тригонометрию (sin, cos, tan).
- Если речь идет о задаче из некого сюжета, можно смело предположить, что деревья, столбы, стены и так далее образуют прямой угол с землей, если не указано иное.
Реклама
Об этой статье
Эту страницу просматривали 140 209 раз.
Была ли эта статья полезной?
Теорема пифагора
Определение теоремы пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Обозначив гипотенузу буквой — c, катеты буквами a и b получим следующее равенство
c2=a2+b2
Расчёт катета по теореме пифагора
Введите гипотенузу
c =
Введите катет
b =
Формула пифагора для катета
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Расчёт гипотенузы по теореме пифагора
Введите первый катет
a =
Введите второй катет
b =
Формула пифагора для гипотенузы
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Доказательство теоремы пифагора
Дано
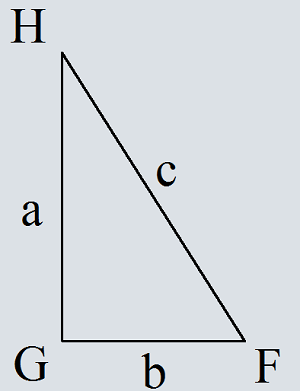
Прямоугольный треугольник с катетами a, b и гипотенузой c.
Доказать
c2=a2+b2
Доказательство
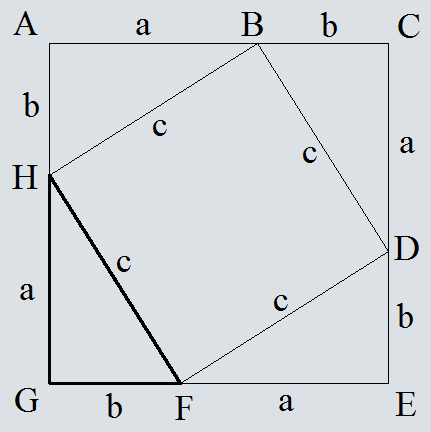
Достроим треугольник HFG до квадрата со стороной a+b.
Запишем площадь получевшегося квадрата двумя способами
S=(a+b)2
S=4*0.5*a*b +c2
Приравняем площади
(a+b)2=4*0.5*a*b +c2
a2+2*a*b +b2=2*a*b +c2
a2+b2=c2
Теорема доказана
Download Article
Download Article
Pythagoras’s Theorem is a formula you can use to find an unknown side length of a right triangle. It is one of the most basic geometric tools in mathematics.[1]
You will likely come across many problems in school and in real life that require using the theorem to solve. In these problems you might need to directly calculate the side length of a triangle, or use right triangles to calculate measurements of other types of polygons.
-
1
Find the right, or 90-degree, angle. Because this theorem only applies to right triangles, you need to determine which angle is the right angle. If the triangle does not have a right angle, you cannot use the theorem.
- Usually the right angle is denoted by a small box.
-
2
Determine that the missing length is the hypotenuse. The hypotenuse is the longest side of a right triangle, and will be opposite the right angle.[2]
Advertisement
-
3
Write the formula for Pythagoras’s Theorem. The formula is
, where
is the length of the hypotenuse, and
and
are the lengths of the other sides of the triangle.[3]
-
4
-
5
Square the length of the sides. Plug these new values into the formula.
-
6
Add the squared length of the sides. This sum is equal to the length of the hypotenuse squared (
).
-
7
Find the square root of both sides of the equation. This will give you the length of your hypotenuse.
-
8
Use the theorem to find the sides of triangles. If you know the hypotenuse and one side of the triangle, you can still use the theorem by substituting for the appropriate values.
Advertisement
-
1
Ensure that you have the measurements for all three sides of the triangle. If you do not have all three side lengths, you cannot use the Pythagorean Theorem to determine whether the triangle is right.
- For example, you might be given a triangle with side lengths of 8, 9, and 12 cm, and you need to determine whether the triangle is right.
-
2
Write the formula for Pythagoras’s Theorem. The formula is
, where
is the length of the hypotenuse, and
and
are the lengths of the other sides of the triangle.[4]
-
3
Plug the length of the potential hypotenuse into the formula. The hypotenuse is the longest side of a right triangle, so whatever measurement is largest will stand for the variable
.
- For example, if the side lengths of a triangle are 8, 9, and 12 cm, you would use the measurement of 12 for the potential hypotenuse, because it’s the longest side. So, your formula will look like this:
.
- For example, if the side lengths of a triangle are 8, 9, and 12 cm, you would use the measurement of 12 for the potential hypotenuse, because it’s the longest side. So, your formula will look like this:
-
4
-
5
Square all of the numbers. Remember that squaring a number means to multiply it by itself.
-
6
Add the square of the two sides. If this sum is equal to the square of the hypotenuse, the triangle is right. If the two sides of the equation are not equal, the triangle is not right.[5]
Advertisement
-
1
Ensure the polygon is a rectangle. A rectangle is a four-sided shape with four 90-degree angles.[6]
-
2
Make sure you have the length and width of the rectangle. If you do not have these measurements, you cannot use this method.
- For example, you might be asked to use the Pythagorean Theorem to find the length of the diagonal of a 6-inch by 4-inch rectangle.
-
3
Locate or draw the diagonal of the rectangle. Since the diagonal of a rectangle divides the shape into two congruent right triangles, you can use Pythagoras’s Theorem to find its length.
- The length of the diagonal will equal the length of the hypotenuse of the right triangles.
-
4
Set up the formula for Pythagoras’s Theorem. The formula is
, where
is the length of the hypotenuse, and
and
are the lengths of the other sides of the triangle.[7]
-
5
-
6
Square the length and width. Remember that squaring means to multiply a number by itself.
-
7
Add the squared side lengths. This sum will give you the value of the hypotenuse, or diagonal, squared.
-
8
Find the square root of both sides. This will give you the value of
, which is the length of the right triangle’s hypotenuse, and also the length of the rectangle’s diagonal.
Advertisement
-
1
Find the shortest distance between two points. For instance, Luis walks through a park. He starts at the fountain and walks 80 feet south and 60 feet west. What is the shortest distance back to the fountain?
-
2
Find a missing length. For instance, find the length of
, given a right triangle with a hypotenuse measuring 10 cm and one side measuring 6 cm.
-
3
Identify a right triangle. For instance, determine whether the triangle is right, given side lengths of 9, 12, and 15 cm.
-
4
Use the diagonal of a rectangle as the hypotenuse of a right triangle. For instance, Sherrie is buying a new computer screen. It needs to be less than 12 inches high to be able to fit under the shelf over her desk. She finds a computer screen with a 27-inch diagonal, and a width of 24 inches. Will this screen fit on her desk?
Advertisement
Add New Question
-
Question
How do I prove that angle A is equal to angle B?
There are many ways to prove two angles equal. Among them are: show that corresponding sides of the angles are parallel to each other; show that they are opposite angles in a rectangle, parallelogram, isosceles triangle or isosceles trapezoid; show that they are formed by two perpendicular lines; or show that they are corresponding angles of congruent or similar triangles. There are also several other ways to prove angles equal.
-
Question
What if I only know one side?
To use the Pythagorian Theorem you MUST know two sides. This may mean you have to use trigonometry to find another side. If you are still confused, ask your teacher.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
To find the square root of a number, use a scientific calculator. Type in the number, then hit the square root button.
-
When doing word problems about traveling, if you are meant to find the shortest distance you will likely use the Pythagorean Theorem. The shortest distance will be the length of the hypotenuse of a triangle superimposed over the area.
-
Learn the most common Pythagorean triples by heart. Since they will occur in a lot of basic Pythagorean theorem problems, being able to instantly recognise them will save you a whole lot of time.
- The most common Pythagorean triples are (3, 4, 5), (5, 12, 13), (8, 15, 17) and (7, 24, 25).
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 40,498 times.
Did this article help you?
Get all the best how-tos!
Sign up for wikiHow’s weekly email newsletter
Subscribe
You’re all set!
Теорема Пифагора является основополагающим звеном в Евклидовой геометрии, на котором базируются большая часть всех вытекающих из теоремы Пифагора следствий и других теорем. Выведенная еще в VI веке до нашей эры, теорема связывает стороны прямоугольного треугольника простым уравнением, и имеет множество доказательств, одно из которых объединяет в себе как алгебру, так и геометрию.
Согласно теореме Пифагора, в прямоугольном треугольнике есть катеты a и b – это стороны прилегающие к прямому углу, и сумма их квадратов дает квадрат гипотенузы – третьей стороны треугольника, лежащей напротив прямого угла.
Доказать это можно, построив четыре прямоугольных треугольника так, чтобы на длинном катете каждого из них был расположен короткий катет следующего треугольника, при этом вершины углов совпадают.
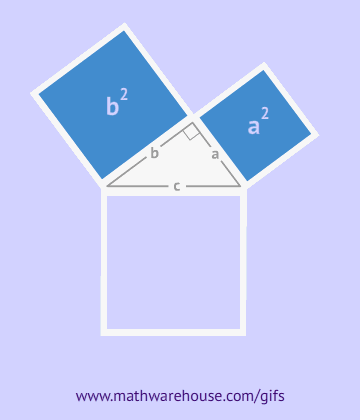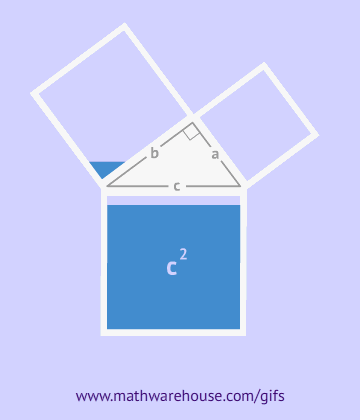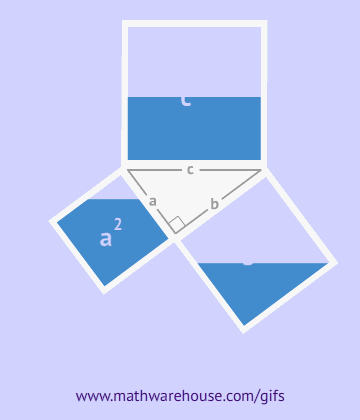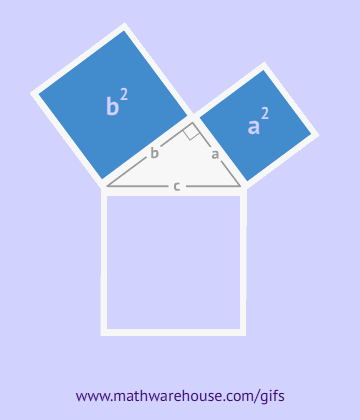
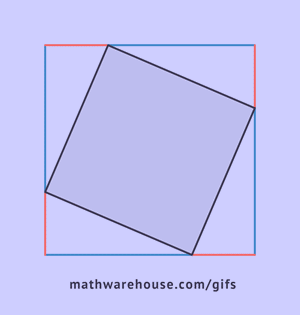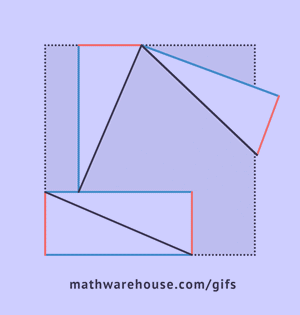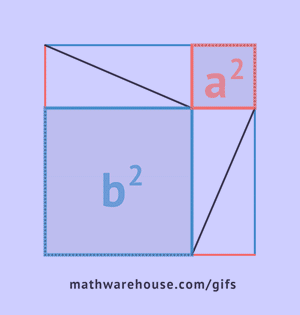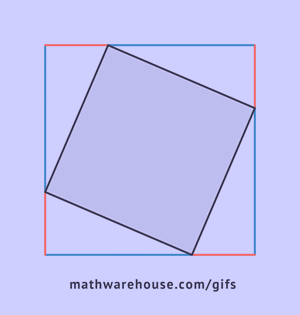
Как видно из рисунка, общая фигура представляет собой квадрат со стороной c, являющей одновременно гипотенузой данных треугольников, а площадь этой фигуры равна c2, согласно формуле площади квадрата. Помимо того, что этот квадрат включает в себя четыре прямоугольных треугольника площадью 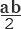
Представим площадь большого квадрата в виде суммы площадей маленького квадрата и четырех треугольников по принципу суперпозиции.
Таким образом, площадь квадрата одновременно равна гипотенузе во второй степени и сумме катетов во вторых степенях, что и требовалось доказать. a2+b2=c2
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):