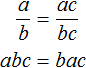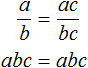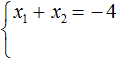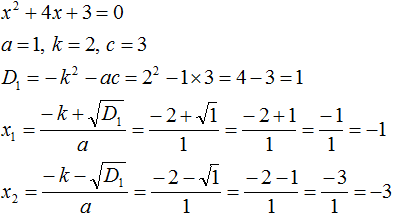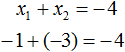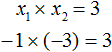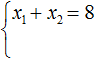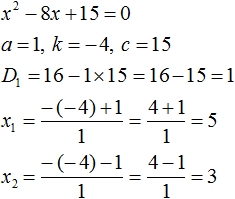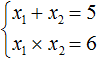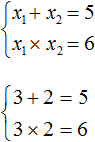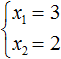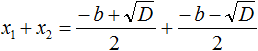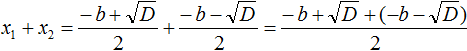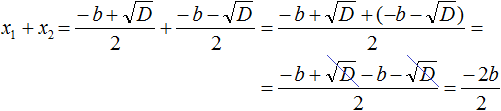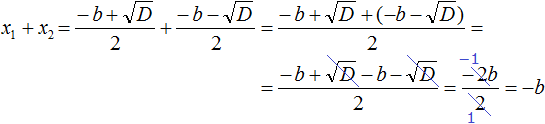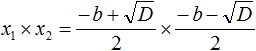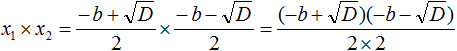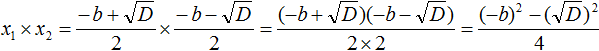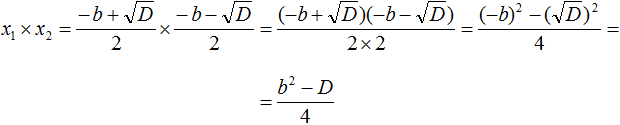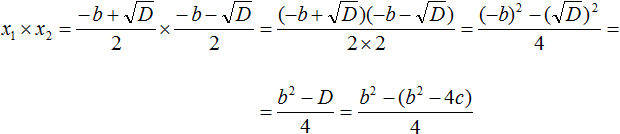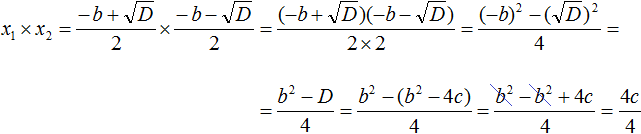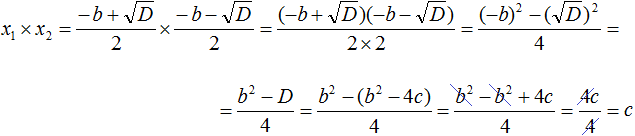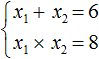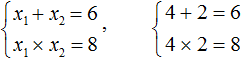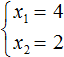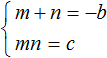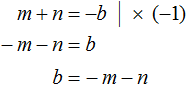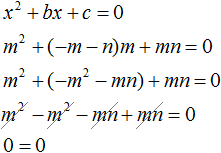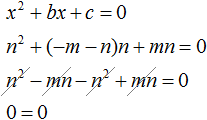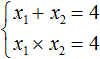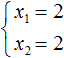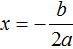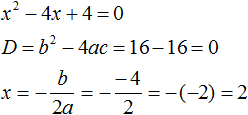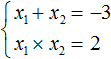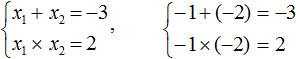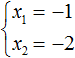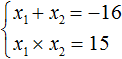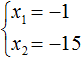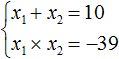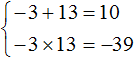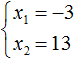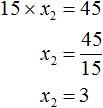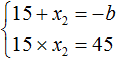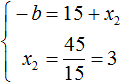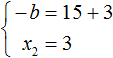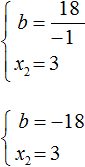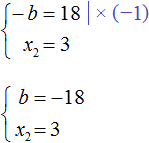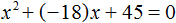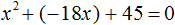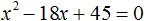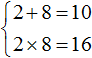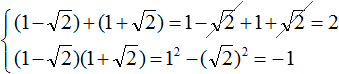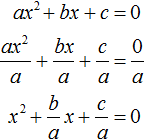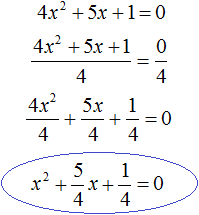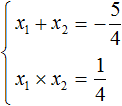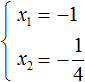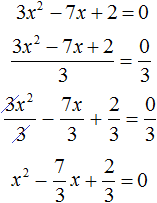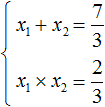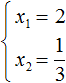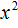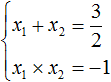Как найти подбором положительный корень уравнения

Теорема Виета для квадратного уравнения

О чем эта статья:

Основные понятия

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Существует три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:

• если D 0, есть два различных корня.

В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .

В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.

Доказательство теоремы Виета

Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

• x₁ + x₂ = −b,
• x₁ * x₂ = c.

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

Объединим числитель и знаменатель в правой части.

Раскроем скобки и приведем подобные члены:

Сократим дробь полученную дробь на 2, остается −b:

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:

Перемножаем числители и знаменатели между собой:

Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:

Далее произведем трансформации в числителе:

Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.

Далее раскроем скобки и приведем подобные члены:

Сократим:

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Докажем теорему, обратную теореме Виета

Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.

Зафиксируем, что сумма m и n равна −b, а произведение равно c.

Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.

Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:

Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:

При x = m получается верное равенство. Значит число m является искомым корнем.

1. Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.

   При x = n получается верное равенство. Значит число n является искомым корнем.

Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.

Примеры

Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.

Дано: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>

Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.

Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>

Неприведенное квадратное уравнение

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax 2 + bx + c = 0, где а = 1.

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .

1. Получилось следующее приведенное уравнение:

Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:

Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.

Получилось приведённое квадратное уравнение. Второй коэффициент которого равен, а свободный член.

Тогда в соответствии с теоремой Виета получаем:

Метод подбора помогает найти корни: −1 и

Теорема Виета

Что называют теоремой?

Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.

Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.

Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.

Например, теоремой можно назвать следующее утверждение:

«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».

А затем привести такое доказательство:

Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с . Тогда полýчится дробь . Докáжем, что дроби и равны. То есть докажем, что равенство является верным.

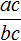
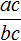
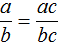
Для доказательства этого равенства воспользуемся основным свойством пропорции:

От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:

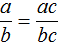
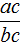
Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.

Теорема Виета

Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:

Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.

То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x₁ и x₂ , то справедливы следующие два равенства:

Знак системы (фигурная скобка) говорит о том, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .

Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:

А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:

Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:

Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x₁ + x₂ к этому коэффициенту, то получается верное равенство:

А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:

Значит выражение 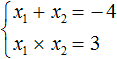является справедливым.

Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:

А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:

Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:

Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.

А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .

Значит выражение 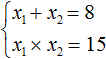является справедливым.

Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.

Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:

Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:

А значит записывать выражение 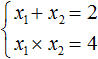не имеет смысла.

Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.

Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x₁ × x₂ = 6 будет выполняться только в двух случаях: если значения x₁ и x₂ положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x₁ + x₂ = 5 , поскольку его правая часть равна положительному числу. А значения x₁ и x₂ должны удовлетворять как равенству x₁ + x₂ = 5 , так и равенству x₁ × x₂ = 6.

Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x₁ + x₂ = 5 так и равенству x₁ × x₂ = 6 . Очевидно, что таковыми являются корни 3 и 2

Доказательство теоремы Виета

Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Вспомним формулы корней квадратного уравнения:

Найдём сумму корней x₁ и x₂ . Для этого подставим в выражение x₁ + x₂ вместо x₁ и x₂ соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2

Запишем правую часть в виде дроби с одним знаменателем:

Раскроем скобки в числителе и приведём подобные члены:

Сократим дробь 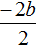на 2 , тогда получим −b

Теперь аналогично докажем, что произведение x₁ × x₂ равно свободному члену c .

Подставим вместо x₁ и x₂ соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:

Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:

В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится 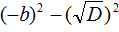А знаменатель будет равен 4

Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение 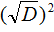станет равно просто D

Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c

В получившемся выражении раскроем скобки в числителе и приведём подобные члены:

Сократим получившуюся дробь на 4

Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x₁ + x₂ = −b ), а произведение корней равно свободному члену ( x₁ × x₂ = c ). Теорема доказана.

Теорема, обратная теореме Виета

Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x₁ и x₂ равно свободному члену уравнения x 2 + bx + c = 0, то числа x₁ и x₂ являются корнями уравнения x 2 + bx + c = 0.

Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.

Так, доказывая теорему Виета мы пришли к заключению, что сумма x₁ и x₂ равна −b , а произведение x₁ и x₂ равно c . В обратной же теореме это заключение служит утверждением.

Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:

А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .

Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.

В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.

Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8

Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x₁ + x₂ = 6 , так и равенству x₁ × x₂ = 8

Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x₁ × x₂ = 8 нужно найти такие x₁ и x₂ , произведение которых равно 8.

Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.

4 × 2 = 8
1 × 8 = 8

Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли не только равенству x₁ × x₂ = 8 , но и равенству x₁ + x₂ = 6 .

Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x₁ × x₂ = 8 , но не удовлетворяют равенству x₁ + x₂ = 6 .

Зато значения 4 и 2 подходят как равенству x₁ × x₂ = 8 , так и равенству x₁ + x₂ = 6 , поскольку эти значения удовлетворяют обоим равенствам:

Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .

Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x₁ и x₂ обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:

Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0

Для начала запишем, что сумма m и n равна −b , а произведение mn равно c

Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .

Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1

Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b

Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .

Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .

Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.

Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .

Примеры решения уравнений по теореме, обратной теореме Виета

Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.

Запишем сумму корней x₁ и x₂ и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x₁ и x₂ и приравняем его к свободному члену :

В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4

Значение x₁ совпадает с x₂ . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле

Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x₁ и x₂ совпадают.

Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Теперь подберём значения x₁ и x₂ . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x₁ + x₂ равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.

Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.

Если подберём корни с разными знаками, то не будет выполняться равенство x₁ × x₂ = 2 .

Если подберем положительные корни, то будет выполняться равенство x₁ × x₂ = 2 , но не будет выполняться равенство x₁ + x₂ = −3 .

Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.

Тогда равенствам будут удовлетворять числа −1 и −2 .

Итак, корнями являются числа −1 и −2

Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.

Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.

Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15

Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10

Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13

Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .

По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45

При этом один из корней уже известен — это корень 15 .

Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3

Этот второй корень также можно было бы получить, выразив из равенства 15 × x₂ = 45 переменную x₂

Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:

По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:

Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:

Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45

Из этой системы следует найти x₂ и b . Выразим эти параметры:

Из этой системы мы видим, что x₂ равно 3. Подставим его в первое равенство:

Теперь из первого равенства мы видим, что −b равно 18

Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18

Этот же результат можно получить если в выражении 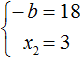умножить первое равенство на −1

Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b

Выполним умножение −18 на x . Получим −18x

Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .

В этом задании корни уже известны. То есть x₁ = 2 , x₂ = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .

Запишем сумму и произведение корней:

По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .

Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .

Значит b = −10 , c = 16 . Отсюда:

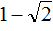
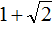
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа и .

Запишем сумму и произведение корней:

Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:

Когда квадратное уравнение неприведённое

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.

Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .

Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a

Получилось уравнение 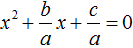, которое является приведённым. В нём второй коэффициент равен , а свободный член равен . Тогда сумма и произведение корней будут выглядеть так:

Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4

Получили приведённое квадратное уравнение. В нём второй коэффициент равен , а свободный член . Тогда по теореме Виета имеем:

Отсюда методом подбора находим корни −1 и

Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.

Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0

Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.

Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2

Получили уравнение 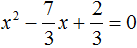. Запишем сумму и произведение корней этого уравнения:

Отсюда методом подбора находим корни 2 и

Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0

Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2

Далее если −3x разделить на 2 , то полýчится 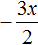. Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде

Далее если −2 разделить на 2 , то полýчится −1

Прирáвниваем получившееся выражение к нулю:

Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:

Отсюда методом подбора находим корни 2 и

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Автор проекта:

Шелкова Полина,

Класс: 10

Руководитель:

Злобова Людмила Викторовна,

учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

• Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
• Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
• Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

• познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
• изучить соответствующую литературу;
• научиться решать тригонометрические уравнения;
• найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
• научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
• подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx=cos2x;

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos²x−sin²x]

sinx−(cos²x−sin²x)=0;

sinx−(1−sin²x−sin²x)=0;

sinx−(1−2sin²x)=0;

2sin²x+sinx−1=0.

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

2t²+t-1=0

D=b²-4ac, т.е. D=9

t₁ = -1, t₂ = ½.

Вернемся к замене:

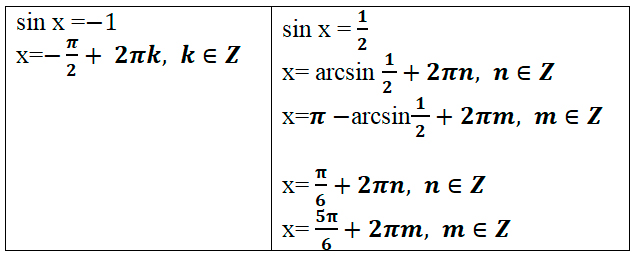
б) Рассмотрим три способа отбора корней, попадающих в отрезок .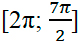

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

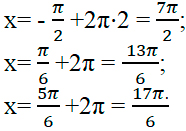
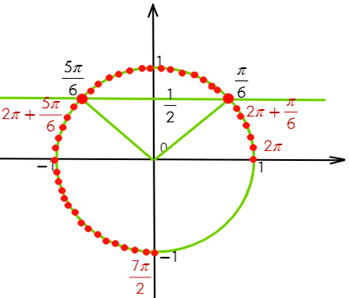
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: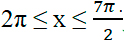

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

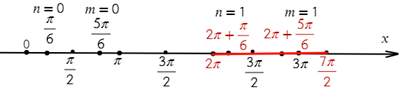
Нам останется только выбрать корни, которые попали в нужный нам отрезок.

Ответ:

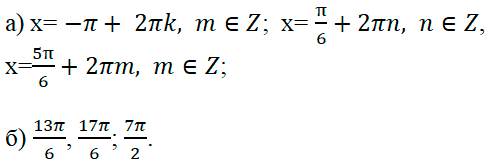
(Более подробный пример в приложении №1)

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
2. Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
3. С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
4. Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.

Электронные ресурсы

1. https://ru.wikipedia.org/wiki/Тригонометрия
2. https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
3. https://mat.1sept.ru/1999/no19.htm

4. Геометрия. Урок 1. Тригонометрия

5. https://math-ege.sdamgia.ru/
6. https://alexlarin.net/ege21.html
7. https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
8. http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
9. https://reshimvse.com/article.php?id=100

План урока:

Целое уравнение и его степень

Решение уравнений методом подбора корня

Решение уравнений с помощью разложения многочлена на множители

Графический метод решения уравнений

Решение дробно-рациональных уравнений

Целое уравнение и его степень

Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:

х – 5;

(а³ + 6а)(а – 5а²);

(n³ + 7)/5 (в знаменателе находится только число, без переменной);

А вот примеры нецелых выражений:

Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.

Введем понятие целого уравнения.

Приведем примеры целых ур-ний:

0,75х⁷ + 0,53х⁶ – 45х = 18

Напомним, что в математике существует понятие равносильных уравнений.

Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).

Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.

Пример. Преобразуйте целое ур-ние

так, чтобы слева стоял многочлен, а справа – ноль.

Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:

Теперь раскроем скобки:

4(5х³ – 3х⁴ + 45х – 27х²) – 40 = 10х² + 5х + 35

20х³ – 12х⁴ + 180х – 108х² – 40 = 10х² + 5х + 35

Осталось перенести все слагаемые влево и привести подобные слагаемые:

20х³ – 12х⁴ + 180х – 108х² – 40 – 10х² – 5х – 35 = 0

– 12х⁴ + 20х³ – 118х² + 175х – 75 = 0

Получили ур-ние в той форме, которую и надо было найти по условию.

Ответ:– 12х⁴ + 20х³ – 118х² + 175х – 75 = 0

В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.

Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике

Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.

Пример. Определите степень ур-ния

(х³ – 5)(2х + 7) = 2х⁴ + 9

Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:

(х³ – 5)(2х + 7) = 2х⁴ + 9

2х⁴ + 7х³ – 10х – 35 = 2х⁴ + 9

Перенесем все слагаемые влево и приведем подобные слагаемые:

2х⁴ + 7х³ – 10х – 35 – 2х⁴ – 9 = 0

7х³ – 10х – 44 = 0

Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень

Ответ: 3

Приведем примеры ур-ний первой степени:

5х + 8 = 0

9z– 6 = 0

5,4568у + 0,0002145 = 0

Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.

Приведем примеры ур-ний второй степени:

6t² + 98t – 52 = 0

54у + 23у = 0

12x²– 65 = 0

Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу

Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:

2х³ + 4х² – 19х + 17 = 0

у³ – 5у + 7 = 0

Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:

5х⁴ + 6х³ – 2х² – 10х + 1 = 0

Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.

Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.

Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k₁, k₂,k₃,…k_n. Приравняем к нулю следующее произведение скобок:

(х – k₁)(х – k₂)(х – k₃)…(х – k_n) = 0

Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния

(х – k₁)(х – k₂)(х – k₃)…(х – k_n) = 0

надо каждую скобку приравнять к нулю:

х – k₁ = 0 или х – k₂ = 0 или х – k₃ = 0 или…х – k_n = 0

Перенесем второе слагаемое вправо в каждом равенстве и получим:

х = k₁ или х = k₂ или х = k₃ или…х = k_n

Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.

Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.

Запишем целое ур-ние, имеющее требуемые корни:

(х – 1)(х – 2)(х – 3)(х – 4) = 0

Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:

(х² – 3х + 2)(х – 3)(х – 4) = 0

(х³ – 6х² + 11х – 6)(х – 4) = 0

х⁴ – 10х³ + 35х² – 50х +24 = 0

Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.

Ответ: х⁴ – 10х³ + 35х² – 50х +24 = 0

Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k₁), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.

Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k₁, k₂,k₃,…k_n, k_n+1 и запишем уравнение:

(х – k₁)(х – k₂)(х – k₃)…(х – k_n)(х – k_n+1) = 0

Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.

Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k₁, k₂,k₃,…k_n, то этому ур-нию равносильна запись (х – k₁)(х – k₂)(х – k₃)…(х – k_n) = 0

Этот факт будет использован далее при решении ур-ний.

Решение уравнений методом подбора корня

Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!

Пример. Докажите, что корнями ур-ния

х³ – 2х² – х + 2 = 0

являются только числа (– 1), 1 и 2.

Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:

(– 1)³ – 2(– 1)² – (– 1) + 2 = 0

–1 – 2 + 1 + 2 = 0

0 = 0

При х = 1 получаем:

1³ – 2•1² – 1 + 2 = 0

1 – 2 – 1 + 2 = 0

0 = 0

Наконец, рассмотрим случай, когда х = 2

2³ – 2•2² – 2 + 2 = 0

8 – 8 – 2 + 2 = 0

0 = 0

Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.

Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.

Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:

а₀xⁿ + a₁x^n–1 + … + а_n–1х + а_n = 0

Числа а₀, а₁, а₂,…а_nи называют коэффициентами уравнений.

Например, для уравнения

5х⁴ – 7х³ + 9х² – х + 12 = 0

коэффициенты равны

а₀ = 5

а₁ = – 7

а₂ = 9

а₃ = – 1

а₄ = + 12

Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии

х³ + 2х – 15 = 0

нет слагаемого с буквенной частью х². Можно считать, что ур-ние равносильно записи

х³ + 0х² + 2х – 15 = 0

где слагаемое х² есть, но перед ним стоит ноль. Тогда коэффициент а₁ = 0.

Для обозначения первого коэффициента а₀ может использоваться термин старший коэффициент, а для последнего коэффициента а_n – термин «свободный член» или «свободный коэффициент».

Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:

Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами

а₀xⁿ + a₁x^n–1 + … + а_n–1х + а_n = 0

Тогда можно подставить туда число m и получить верное равенство:

а₀mⁿ + a₁m^n–1 + … + а_n–1m + а_n = 0

Поделим обе его части на m и получим

а₀m^n–1 + a₁m^n–2 + … + а_n–1 + а_n/m = 0

Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а₀m^n–1, a₁m^n–2, а_n–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число а_n/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа а_n.

Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.

Пример. Найдите целые корни уравнения

2х⁴ – х³ – 9х² + 4х + 4 = 0

Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):

2•1⁴ – 1³ – 9•1² + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0

2•2⁴ – 2³ – 9•2² + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0

2•(– 2)⁴ – (– 2)³ – 9•(– 2)² + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0

Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.

Ответ: 1; 2; (– 2).

Пример. Решите ур-ние

0,5х³ + 0,5х + 5 = 0

Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:

0,5х³ + 0,5х + 5 = 0

(0,5х³ + 0,5х + 5)•2 = 0•2

х³ + х + 10 = 0

Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:

(– 2)³ + (– 2) + 10 = – 8 – 2 + 10 = 0

Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х³ и у = х + 10. Значит, и вся левая часть х³ + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.

Ответ: – 2

Ещё быстрее можно узнать, является ли единица корнем уравнения.

Докажем это. Подставим в ур-ние

а₀xⁿ + a₁x^n–1 + … + а_n–1х + а_n = 0

значение х = 1. Так как единица в любой степени равна самой единице, то получим:

а₀1ⁿ + a₁1^n–1 + … + а_n–11 + а_n = 0

а₀ + a₁ + … + а_n–1 + а_n = 0

Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.

Пример. Укажите хотя бы 1 корень ур-ния

499х¹⁰ – 9990х⁷ + 501х⁶ – 10х⁵ + 10000х⁴ – 1000 = 0

Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:

499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0

Следовательно, единица является его корнем.

Ответ: 1.

Решение уравнений с помощью разложения многочлена на множители

Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.

Пример. Решите ур-ние

х⁴ – 16 = 0

Решение. Степень х⁴ можно представить как (х²)², а 16 – как 4². Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:

х⁴ – 16 = 0

(х² – 4)(х² + 4) = 0

Приравняем каждую скобку к нулю и получим два квадратных ур-ния:

х² – 4 = 0 или х² + 4 = 0

х² = 4 или х² = – 4

Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.

Ответ: 2 и (– 2).

Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние

100х³ – 210х² + 134х – 24 = 0

Можно заметить, сумма всех коэффициентов ур-ния равна нулю:

100 – 210 + 134 – 24 = 0

Следовательно, первый корень – это 1.

Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k₁, k₂и k₃. Тогда ему равносильно другое ур-ние

(х – k₁)(х – k₂)(х – k₃) = 0

Мы нашли, что первый корень k₁ = 1, то есть

(х – 1)(х – k₂)(х – k₃) = 0

Обозначим как P₁(x) = 0 ещё одно ур-ние, корнями которого будут только числа k₂ и k₃. Очевидно, что корнями ур-ния

(х – 1)•P₁(x) = 0

Будут числа 1, k₂ и k₃. Его корни совпадают с корнями исходного ур-ния, а потому запишем

(х – 1)•P₁(x) = 100х³ – 210х² + 134х – 24

Поделим обе части на (х – 1):

Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р₁(х), причем решением уравнения P₁(x) = 0 будут оставшиеся два корня, k₂и k₃. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:

Смотрим на первое слагаемое делимого. Это 100х³. На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х³? Это 100х². Действительно, (х – 1)100х² = 100х³ – 100х². Запишем слагаемое 100х² в результат деления, а результат его умножения на делитель, то есть 100х³ – 100х², вычтем из делимого:

Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х³, естественно, сократятся:

(100х³ – 210х²) – (100х³ – 100х²) = 100х³ – 210х² – 100х³ + 100х² = – 110х²

Далее снесем слагаемое 134х вниз:

На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х²). Очевидно, на (– 110х):

(х – 1)(– 110х²) = –110х² + 110х

Запишем в поле «ответа» слагаемое (– 110х²), а под делимый многочлен – результат его умножения на (х – 1):

При вычитании из (–110х² + 134х) полинома (–110х² + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:

Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:

В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х³ – 210х² + 134х – 24 на множители:

100х³ – 210х² + 134х – 24 = (х – 1)(100х² – 110х + 24)

Теперь перепишем исходное ур-ние с учетом этого разложения:

100х³ – 210х² + 134х – 24 = 0

(х – 1)(100х² – 110х + 24) = 0

Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:

100х² – 110х + 24 = 0

D =b² – 4ас = (– 110)² – 4•100•24 = 12100 – 9600 = 2500

Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.

В данном случае мы воспользовались следующим правилом:

Пример. Решите уравнение

2х³ – 8х² + 16 = 0

Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:

2•2³ – 8•2² + 16 = 16 – 32 + 16 = 0

Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х³ – 8х² + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:

2х³ – 8х² + 16 = 2х³ – 8х² + 0х + 16

Теперь возможно деление:

Получили, что 2х³ – 8х² + 16 = (х – 2)(2х – 4х –

С учетом этого перепишем исходное ур-ние:

2х³ – 8х² + 16 = 0

(х – 2)(2х – 4х – = 0

х – 2 = 0 или 2х – 4х – 8 = 0

Решим квадратное ур-ние

D =b² – 4ас = (– 4)² – 4•2•(– = 16 + 64 = 80

В 8 классе мы узнали, что если у квадратного ур-ния ах² + bx + c = 0 есть два корня, то многочлен ах² + bx + c можно разложить на множители по формуле

ах² + bx + c = а(х – k₁)(х – k₂)

где k₁ и k₂– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k₁, k₂ и k₃, то его можно разложить на множители по формуле

ах³ +bx² + cx + d = a(х – k₁)(х – k₂)(х – k₃)

Пример. Разложите на множители многочлен 2х³ – 4х² – 2х + 4.

Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:

2•1³ – 4•1² – 2•1 + 4 = 2 – 4 – 2 + 4 = 0

2•(– 1)³ – 4•(– 1)² – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0

2•2³ – 4•2² – 2•2 + 4 = 16 – 16 – 4 + 4 = 0

Значит, многочлен можно разложить на множители:

2х³ – 4х² – 2х + 4 = 2(х + 1)(х – 1)(х – 2)

Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:

(х + 1)(х – 1)(х – 2) = (х² – 1)(х – 2) = х³ – 2х² – х + 2

Получили не тот многочлен, который стоит в условии. Однако ур-ние

х³ – 2х² – х + 2 = 0

имеет те же корни (1, 2 и (– 1)), что и ур-ние

2х³ – 4х² – 2х + 4 = 0

Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:

2•(х³ – 2х² – х + 2) = 2х³ – 4х² – 2х + 4

Надо понимать, что хотя ур-ния 2х³ – 4х² – 2х + 4 = 0 и х³ – 2х² – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k₁), (х – k₂), (х – k₃) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:

2х³ – 4х² – 2х + 4= 2•(х³ – 2х² – х + 2) = 2(х + 1)(х – 1)(х – 2)

Ответ: 2(х + 1)(х – 1)(х – 2).

Графический метод решения уравнений

Любое ур-ние с одной переменной можно представить в виде равенства

у(х) = g(x)

где у(х) и g(x) – некоторые функции от аргумента х.

Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.

Пример. Решите графически уравнение

х³ – х² – 1 = 0

Решение. Строить график уравнения х³ – х² – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х² – 1) вправо:

х³ – х² – 1 = 0

х³ = х² + 1

Построим графики у = х³ и у = х² + 1 (второй можно получить переносом параболы у = х² на единицу вверх):

Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.

Ответ: х ≈ 1,46557

Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.

Пример. Определите количество корней уравнений

а)х³ – х – 3 = 0

б) х³ – 2х + 0,5 = 0

Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:

а) х³ = х + 3

б) х³ = 2х – 0,5

Построим графики функций у = х³, у = х + 3 и у = 2х – 0,5:

Видно, что прямая у = х + 3 пересекает график у = х³ в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.

Ответ: а) один корень; б) три корня.

Решение дробно-рациональных уравнений

До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.

Приведем несколько примеров ур-ний, считающихся дробно-рациональными:

С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:

Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.

Обычно для решения дробно-рациональных уравнений используют такой алгоритм:

1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.

2) Решают полученное целое ур-ние.

3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.

Пример. Решите ур-ние

Решение.

Умножим обе части равенства на знаменатель 1-ой дроби:

2х² – 3х – 2 = х²(х – 2)

Раскроем скобки и перенесем все слагаемые в одну сторону:

2х² – 3х – 2 = х³– 2х²

х³ – 2х² – 2х² + 3х + 2 = 0

х³ – 4х² + 3х + 2 = 0

У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:

2³ – 4•2² + 3•2 + 2 = 8 – 16 + 6 + 2 = 0

Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):

Получили, что х³ – 4х² + 3х + 2 = (х – 2)(х² – 2х – 1)

Тогда ур-ние примет вид:

(х – 2)(х² – 2х – 1) = 0

х – 2 = 0 или х² – 2х – 1 = 0

Решим квадратное ур-ние:

D =b² – 4ас = (– 2)² – 4•1•(– 1) = 4 + 4 = 8

Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии

в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:

х – 2 = 2 – 2 = 0

Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.

Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:

Пример. Найдите все корни ур-ния

Решение. Если сразу привести выражение слева к общему знаменателю 4(х² + х – 2)(х² + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х² + х как у:

у = х² + х

Тогда уравнение примет вид

Приведем дроби к общему знаменателю 4(у – 2)(у – 20):

Знаменатель должен равняться нулю:

4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0

4у – 80 + 28у – 56 + у² – 20у – 2у + 40 = 0

у² + 10у – 96 = 0

Решаем квадратное ур-ние:

D =b² – 4ас = (10)² – 4•1•(– 96) = 100 + 384 = 484

Получили, что у₁ = – 16, а у₂ = 6. Произведем обратную замену:

у = х² + х

х² + х = – 16 или х² + х = 6

х² + х + 16 = 0 или х² + х – 6 = 0

Дискриминант 1-ого ур-ния отрицателен:

D =b² – 4ас = (1)² – 4•1•(16) = 1– 64 = – 63

А потому оно не имеет решений. Решим 2-ое ур-ние:

D = b² – 4ас = (1)² – 4•1•(– 6) = 1+ 24 = 25

Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии

в ноль. Подстановкой можно убедиться, что не обращают.

Ответ: – 3 и 2.

При решении дробно-рациональных ур-ний может использоваться и графический метод.

Пример. Сколько корней имеет уравнение

Решение. Построим графики функций у = х² – 4 и у = 2/х:

Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.

Ответ: 3 корня.

Всероссийский конкурс для школьных педагогов на лучшую образовательную статью «Просто о сложном»

Автор Лисицына Елена Федоровна.

учитель математики

МБОУ «Гимназия№11»

г. Бийска Алтайского кр.

Методы отбора корней в тригонометрических уравнениях

или

Ох уж эта тригонометрия!

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен в течение уже более 10лет. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Необходимо также знать тригонометрические формулы, табличные значения тригонометрических функций для решения еще целого ряда заданий Единого Государственного Экзамена по математике. Постоянно работая в 10-11 классах, я регулярно сталкивалась с определенными проблемами при работе с вышеуказанным разделом тригонометрии: долго не могла установить баланс между доступностью изложения материала и достаточностью обоснований развернутого решения этой категории заданий. В моей практике были случаи, когда вполне успевающие по математике учащиеся начинали испытывать неуверенность и просто страх при решении тригонометрических уравнений с отбором корней, будь то принадлежность корней области допустимых значений переменной или указанному в задании промежутку. В результате целенаправленной многолетней работы в этом направлении у меня сложилась определенная методика работы с данным разделом, которая оказалась довольно успешной, что подтверждает следующая таблица результатов выполнения учащимися задания №13 профильного ЕГЭ по математике с 2015 по 2021 г.г. ( в % от общего количества учеников 11-х классов гимназии, сдающих профильный ЕГЭ по математике)

В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрического круга или числовой прямой. Тригонометрический круг более удобен, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит полный оборот или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

Моя практика показала, что чаще всего можно обойтись применением тригонометрического круга при отборе корней , а в случае, если промежуток превышает по длине полный оборот- алгебраическим способом. При этом, безусловно, следует познакомить учащихся и с остальными способами. Таким образом, работа над данным разделом разделилась у меня на следующие этапы:

1)Знакомство с устройством тригонометрического круга и отработка умений находить числа и промежутки на нем в ходе выполнения следующих упражнений:

2)Отработка навыков работы с тригонометрическим кругом при решении простейших тригонометрических уравнений с отбором корней , которая предполагает выполнение большого количества упражнений по типу приведенных ниже:

3)Отбор корней в одном и том же уравнении разными способами, чтобы учащиеся имели возможность выбора в соответствии со своими предпочтениями, например

Например,
а) Решить уравнение cos2x=sin(π/2+x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π].

Решим пункт а)Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x);cos2x = cosx ;
cos2x – cosx = 0; cosx(cosx – 1) = 0, т.е.

Решим пункт б).

I . Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π;

Сразу делим все на π или умножаем на 1/ π
–7/2 ≤ 1/2 + n ≤ –2;
–7/2 – 1/2 ≤ n ≤ –2 – 1/2 ;
–4 ≤ n ≤ –5/2.
Целые n в этом промежутке это: n=–4 n= –3.

Значит, корни, принадлежащие этому промежутку, будут следующие:

х= π/2 + π(–4) = –7π/2; х=π/2 + π(–3) = –5π/2.
Аналогично решаем еще два неравенства:
–7π/2 ≤ π/4 + 2πk ≤ –2π;
–15/8 ≤ k ≤ –9/8.
Получили, что целых k в этом промежутке нет.
–7π/2 ≤ –π/4 + 2πm ≤ –2π;
–13/8 ≤ m ≤ –7/8.
Получили одно целое n в этом промежутке, m =–1. Значит, отобранный корень на этом промежутке имеет вид: х= –π/4 + 2π·(–1) = –9π/4.
Ответ: –7π/2, –5π/2, –9π/4.

II. Отбор корней с помощью тригонометрической окружности.

Чтобы использовать этот способ надо понимать, как работать с окружностью. Так как функции синус, косинус, тангенс и котангенс периодичны, то окружность, можно обходить бесконечное число раз.

«Обойдем» окружность один раз против часовой стрелки (положительное направление, т.е. значения будут положительные)

«Обойдем» окружность два раза против часовой стрелки (положительное направление т.е. значения будут положительные)

«Обойдем» 1 раз по часовой стрелки (отрицательное направление, т.е. значения будут отрицательные)

Вернемся к вопросу об отборе корней на промежутке

[–7π/2; –2π].
Чтобы попасть к числам –7π/2 и –2π надо «обойти» окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Предположим n= –2, получаем х=π/2 – 2π = –3π/2, очевидно, это не входит в наш промежуток. Значит, берем меньше n=–3, то х= π/2 – 3π = –5π/2, это подходит. Попробуем еще n=–4, то х=π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для х=π/4 + 2πk, k ∈ Z и х=–π/4 + 2πm, m ∈ Z находим еще один корень x=–9π/4.

После того, как отбор корней произвели разными способами, прошу проанализировать преимущества каждого из них, получились, в частности такие итоги: первый способ (с помощью неравенств) гораздо надежнее и намного проще для понимания, но нужно уметь решать простейшие неравенства. Если действительно серьезно разобраться с тригонометрической окружностью, то отбор корней по второму методу будет гораздо быстрее. Плюс экономия времени на экзамене.

4)Проведение смотра знаний по данной теме в форме математической игры «Своя игра»

(идея заимствована здесь https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia )

5)Рассмотрение реальных работ участников ЕГЭ прошлых лет, оцененных экспертами, с целью нахождения ошибок при выполнении отбора корней в тригонометрических уравнениях, например оценка эксперта-1 балл. Почему не засчитано решение п.б)?

Вывод: отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне принадлежащем отрезку.

Вывод: при отборе корней отсутствует решение и ошибочно указано число, которое не является корнем тригонометрического уравнения.

В заключение отмечу, что поскольку задание № 13 (или №12 в модели профильного ЕГЭ 2022 года) является самым простым из заданий с развернутым решением, то целенаправленная работа над ним дает возможность большему числу выпускников успешно справиться с ним и получить высокий результат на экзамене.

Список используемых ресурсов:

1. Виленкин Н. Я. Алгебра и математический анализ 10 класс. Учебник для углубленного изучения математики в общеобразовательных учреждениях, Издательство Мнемозина, 13-е изд. стереотипное, 2006. — 336с.

2. Гельфанд И.М., Львовский С.М., Тоом А.Л. Тригонометрия, М. : МЦНМО, 2003.-7-16 с.

3. Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

4. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ)//Математика в школе.№3, С.18-27.

5. А.Н. Колмагорова Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений, 17-е изд. – М. : Просвещение, 2008. — 384 с.

6. Королев С.В. Тригонометрия на экзамене по математике, изд. Экзамен, 2006. – 254 с.

7. Марасанов А.Н. О методологическом подходе в обучении тригонометрии/ Н.И. Попов, А.Н. Марасанов// Знание и понимание. Умение. -2008. — №4. — 139-141 с.

8. Марасанов А.Н. Тригонометрия: учебное пособие, 2-е изд., испр и доп. (Н.И. Попов, А.Н. Марасанов.-Йошкар-Ола; Мар. гос. Ун-т, 2009.-114с.)

9. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Тригонометрия. 10 класс, М. : Просвещение, 2008. – 61 с.

10. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 1.Учебник для учащихся общеобразовательных учреждений(базовый уровень). – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил.

11. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений(базовый уровень), – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил. 69

12. Мирошин В. Отбор корней в тригонометрических уравнениях.//Математика. Приложение к газете «Первое сентября» №17, 2006г.

13. Просветов Г.И. Тригонометрия. Задачи и решения, Альфа-Пресс, 2010. – 72 с.

14. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.

15. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений//Математика в школе. 2004. №1. С.24-26.

16. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях//Математика в школе. 2004. №1. С.20-24.

17. https://ppt-online.org/491236

18. Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ЕГЭ 2022 года. МАТЕМАТИКА. Федеральный институт педагогических измерений, 2022

19. https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia