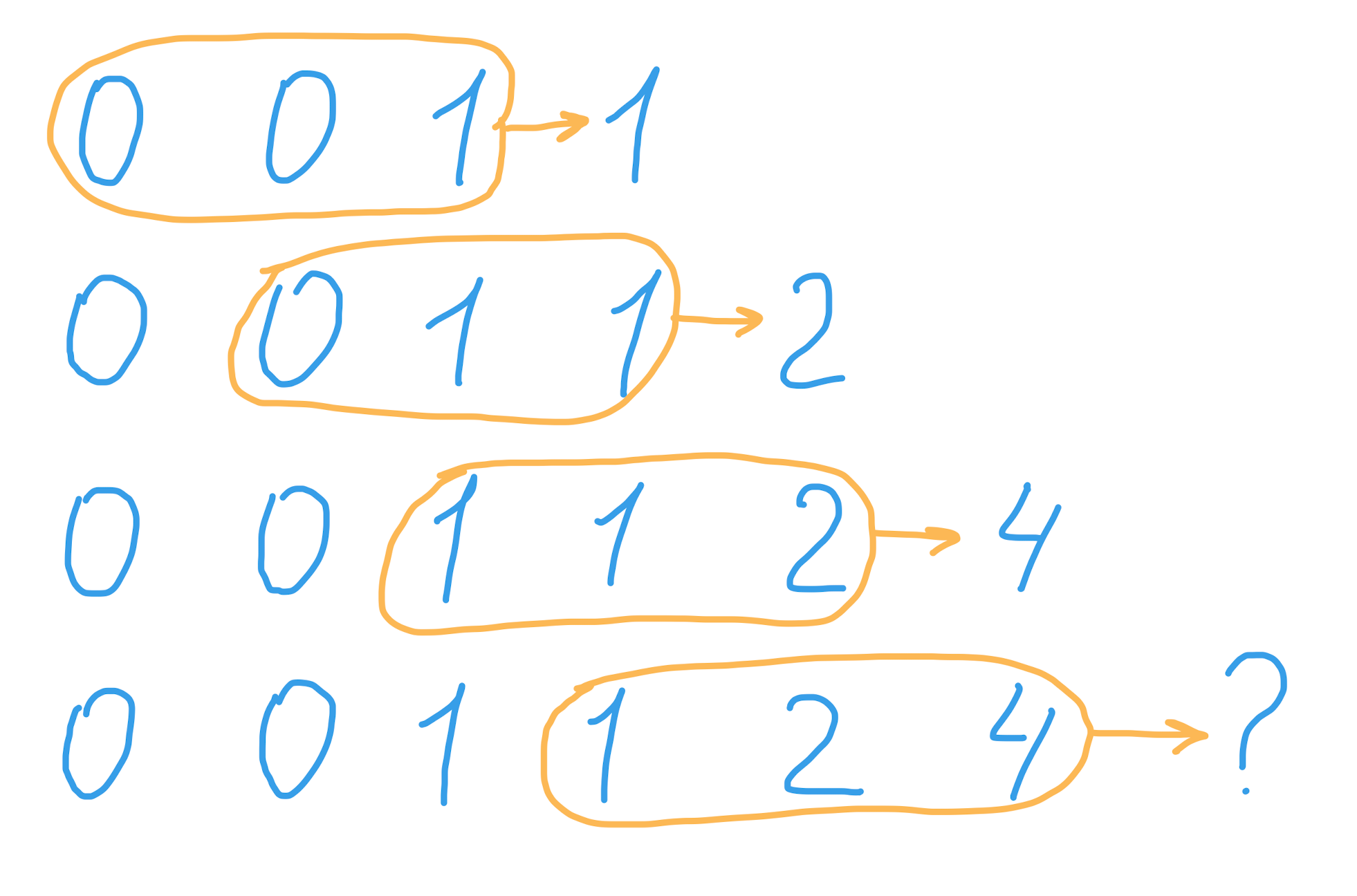Дан целочисленный массив, найдите в нем непрерывный подмассив с наибольшей суммой.
Например,
Input: {-2, 1, -3, 4, -1, 2, 1, -5, 4}
Output: Subarray with the largest sum is {4, -1, 2, 1} with sum 6.
Потренируйтесь в этой проблеме
Задача отличается от задачи нахождения подпоследовательности максимальной суммы. В отличие от подпоследовательностей, подмассивы должны занимать последовательные позиции в исходном массиве.
Мы можем легко решить эту задачу за линейное время, используя Алгоритм Кадане. Идея состоит в том, чтобы поддерживать максимальный (с положительной суммой) подмассив, “заканчивающийся” на каждом индексе данного массива. Этот подмассив либо пуст (в этом случае его сумма равна нулю), либо состоит на один элемент больше, чем максимальный подмассив, оканчивающийся на предыдущем индексе.
Алгоритм может быть реализован следующим образом на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <iostream> #include <vector> using namespace std; // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве int kadane(vector<int> const &arr) { // сохраняет максимальный суммарный подмассив, найденный на данный момент int max_so_far = 0; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int max_ending_here = 0; // обход заданного массива for (int i = 0; i < arr.size(); i++) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + arr[i]; // если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет // пустой подмассив) max_ending_here = max(max_ending_here, 0); // обновить результат, если текущая сумма подмассива окажется больше max_so_far = max(max_so_far, max_ending_here); } return max_so_far; } int main() { vector<int> arr = { —2, 1, —3, 4, —1, 2, 1, —5, 4 }; cout << «The maximum sum of a contiguous subarray is « << kadane(arr); return 0; } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is 6
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
class Main { // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве public static int kadane(int[] arr) { // сохраняет максимальный суммарный подмассив, найденный на данный момент int maxSoFar = 0; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int maxEndingHere = 0; // обход заданного массива for (int i: arr) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) maxEndingHere = maxEndingHere + i; // если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет // пустой подмассив) maxEndingHere = Integer.max(maxEndingHere, 0); // обновить результат, если текущая сумма подмассива окажется больше maxSoFar = Integer.max(maxSoFar, maxEndingHere); } return maxSoFar; } public static void main(String[] args) { int[] arr = { —2, 1, —3, 4, —1, 2, 1, —5, 4 }; System.out.println(«The sum of contiguous subarray with the « + «largest sum is « + kadane(arr)); } } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is 6
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# Функция нахождения максимальной суммы непрерывного подмассива # в заданном целочисленном массиве def kadane(arr): # хранит подсписок максимальной суммы, найденный на данный момент. max_so_far = 0 # хранит максимальную сумму подсписков, заканчивающихся на текущей позиции max_ending_here = 0 # пройти по заданному списку for i in arr: # обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления # текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + i #, если максимальная сумма отрицательна, установите ее на 0 (что означает # пустой подсписок) max_ending_here = max(max_ending_here, 0) # обновляет результат, если сумма текущего подсписка оказывается больше max_so_far = max(max_so_far, max_ending_here) return max_so_far if __name__ == ‘__main__’: arr = [—2, 1, —3, 4, —1, 2, 1, —5, 4] print(‘The sum of contiguous sublist with the largest sum is’, kadane(arr)) |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is 6
Временная сложность приведенного выше решения равна O(n) и не требует дополнительного места, где n это размер ввода.
Приведенный выше код не обрабатывает случай, когда все элементы массива отрицательные. Если массив содержит все отрицательные значения, ответом является максимальный элемент. Мы можем легко разместить эту проверку перед тем, как продолжить алгоритм. Реализацию можно увидеть ниже на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
#include <iostream> #include <vector> #include <algorithm> using namespace std; // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве int kadane(vector<int> const &arr) { // находим максимальный элемент в заданном массиве int max_num = *max_element(arr.begin(), arr.end()); // если массив содержит все отрицательные значения, вернуть максимальный элемент if (max_num < 0) { return max_num; } // сохраняет максимальный суммарный подмассив, найденный на данный момент int max_so_far = 0; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int max_ending_here = 0; // обход заданного массива for (int i = 0; i < arr.size(); i++) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + arr[i]; // если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет // пустой подмассив) max_ending_here = max(max_ending_here, 0); // обновить результат, если текущая сумма подмассива окажется больше max_so_far = max(max_so_far, max_ending_here); } return max_so_far; } int main() { vector<int> arr = { —8, —3, —6, —2, —5, —4 }; cout << «The maximum sum of a contiguous subarray is « << kadane(arr); return 0; } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
import java.util.Arrays; class Main { // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве public static int kadane(int[] arr) { // находим максимальный элемент в заданном массиве int max = Arrays.stream(arr).max().getAsInt(); // если массив содержит все отрицательные значения, вернуть максимальный элемент if (max < 0) { return max; } // сохраняет максимальный суммарный подмассив, найденный на данный момент int maxSoFar = 0; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int maxEndingHere = 0; // делаем для каждого элемента заданного массива for (int i: arr) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) maxEndingHere = maxEndingHere + i; // если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет // пустой подмассив) maxEndingHere = Integer.max(maxEndingHere, 0); // обновить результат, если текущая сумма подмассива окажется больше maxSoFar = Integer.max(maxSoFar, maxEndingHere); } return maxSoFar; } public static void main(String[] args) { int[] arr = { —8, —3, —6, —2, —5, —4 }; System.out.println(«The sum of contiguous subarray with the « + «largest sum is « + kadane(arr)); } } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# Функция нахождения максимальной суммы непрерывного подмассива # в заданном целочисленном массиве def kadane(arr): # найти максимальный элемент, присутствующий в данном списке maximum = max(arr) #, если список содержит все отрицательные значения, вернуть максимальный элемент if maximum < 0: return maximum # хранит подсписок максимальной суммы, найденный на данный момент. max_so_far = 0 # хранит максимальную сумму подсписков, заканчивающихся на текущей позиции max_ending_here = 0 # сделать для каждого элемента заданного списка for i in arr: # обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления # текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + i #, если максимальная сумма отрицательна, установите ее на 0 (что означает # пустой подсписок) max_ending_here = max(max_ending_here, 0) # обновляет результат, если сумма текущего подсписка оказывается больше max_so_far = max(max_so_far, max_ending_here) return max_so_far if __name__ == ‘__main__’: arr = [—8, —3, —6, —2, —5, —4] print(‘The sum of contiguous sublist with the largest sum is’, kadane(arr)) |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Этот подход требует двух обходов входного массива. Мы можем легко модифицировать основной алгоритм, чтобы он обрабатывал и отрицательные целые числа. Алгоритм может быть реализован следующим образом на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <iostream> #include <vector> #include <climits> using namespace std; // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве (также обрабатывает отрицательные числа) int kadaneNeg(vector<int> const &arr) { // сохраняет максимальный суммарный подмассив, найденный на данный момент int max_so_far = INT_MIN; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int max_ending_here = 0; // обход заданного массива for (int i = 1; i < arr.size(); i++) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + arr[i]; // максимальная сумма должна быть больше текущего элемента max_ending_here = max(max_ending_here, arr[i]); // обновить результат, если текущая сумма подмассива окажется больше max_so_far = max(max_so_far, max_ending_here); } return max_so_far; } int main() { vector<int> arr = { —8, —3, —6, —2, —5, —4 }; cout << «The maximum sum of a contiguous subarray is « << kadaneNeg(arr); return 0; } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
class Main { // Функция для нахождения максимальной суммы непрерывного подмассива // в заданном целочисленном массиве (также обрабатывает отрицательные числа) public static int kadaneNeg(int[] arr) { // сохраняет максимальный суммарный подмассив, найденный на данный момент int maxSoFar = Integer.MIN_VALUE; // сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции int maxEndingHere = 0; // обход заданного массива for (int i: arr) { // обновить максимальную сумму подмассива, «заканчивающегося» на индексе «i» (путем добавления // текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе) maxEndingHere = maxEndingHere + i; // максимальная сумма должна быть больше текущего элемента maxEndingHere = Integer.max(maxEndingHere, i); // обновить результат, если текущая сумма подмассива окажется больше maxSoFar = Integer.max(maxSoFar, maxEndingHere); } return maxSoFar; } public static void main(String[] args) { int[] arr = { —8, —3, —6, —2, —5, —4 }; System.out.println(«The maximum sum of a contiguous subarray is « + kadaneNeg(arr)); } } |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import sys # Функция нахождения максимальной суммы непрерывного подмассива # в заданном целочисленном массиве (также обрабатывает отрицательные числа) def kadaneNeg(arr): # хранит подсписок максимальной суммы, найденный на данный момент. max_so_far = —sys.maxsize # хранит максимальную сумму подсписков, заканчивающихся на текущей позиции max_ending_here = 0 # пройти по заданному списку for i in range(len(arr)): # обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления # текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’) max_ending_here = max_ending_here + arr[i] # Максимальная сумма # должна быть больше, чем текущий элемент max_ending_here = max(max_ending_here, arr[i]) # обновляет результат, если сумма текущего подсписка оказывается больше max_so_far = max(max_so_far, max_ending_here) return max_so_far if __name__ == ‘__main__’: arr = [—8, —3, —6, —2, —5, —4] print(‘The sum of contiguous sublist with the largest sum is’, kadaneNeg(arr)) |
Скачать Выполнить код
результат:
The maximum sum of a contiguous subarray is -2
Из-за того, как этот алгоритм использует оптимальные основания (максимальный подмассив, заканчивающийся в каждой позиции, вычисляется просто из связанной, но меньшей и перекрывающейся подзадачи: максимальный подмассив, заканчивающийся в предыдущей позиции), этот алгоритм можно рассматривать как простой пример динамическое программирование.
Связанный пост:
Вывести непрерывный подмассив с максимальной суммой
Использованная литература: https://en.wikipedia.org/wiki/Maximum_subarray_problem
From Wikipedia, the free encyclopedia
Visualization of how sub-arrays change based on start and end positions of a sample. Each possible contiguous sub-array is represented by a point on a colored line. That point’s y-coordinate represents the sum of the sample. Its x-coordinate represents the end of the sample, and the leftmost point on that colored line represents the start of the sample. In this case, the array from which samples are taken is [2, 3, -1, -20, 5, 10].
In computer science, the maximum sum subarray problem, also known as the maximum segment sum problem, is the task of finding a contiguous subarray with the largest sum, within a given one-dimensional array A[1…n] of numbers. It can be solved in 

Formally, the task is to find indices 


is as large as possible. (Some formulations of the problem also allow the empty subarray to be considered; by convention, the sum of all values of the empty subarray is zero.) Each number in the input array A could be positive, negative, or zero.[1]
For example, for the array of values [−2, 1, −3, 4, −1, 2, 1, −5, 4], the contiguous subarray with the largest sum is [4, −1, 2, 1], with sum 6.
Some properties of this problem are:
- If the array contains all non-negative numbers, then the problem is trivial; a maximum subarray is the entire array.
- If the array contains all non-positive numbers, then a solution is any subarray of size 1 containing the maximal value of the array (or the empty subarray, if it is permitted).
- Several different sub-arrays may have the same maximum sum.
Although this problem can be solved using several different algorithmic techniques, including brute force,[2] divide and conquer,[3] dynamic programming,[4] and reduction to shortest paths, a simple single-pass algorithm known as Kadane’s algorithm solves it efficiently.
History[edit]
The maximum subarray problem was proposed by Ulf Grenander in 1977 as a simplified model for maximum likelihood estimation of patterns in digitized images.[5]
Grenander was looking to find a rectangular subarray with maximum sum, in a two-dimensional array of real numbers. A brute-force algorithm for the two-dimensional problem runs in O(n6) time; because this was prohibitively slow, Grenander proposed the one-dimensional problem to gain insight into its structure. Grenander derived an algorithm that solves the one-dimensional problem in O(n2) time,[note 1]
improving the brute force running time of O(n3). When Michael Shamos heard about the problem, he overnight devised an O(n log n) divide-and-conquer algorithm for it.
Soon after, Shamos described the one-dimensional problem and its history at a Carnegie Mellon University seminar attended by Jay Kadane, who designed within a minute an O(n)-time algorithm,[5][6][7] which is as fast as possible.[note 2] In 1982, David Gries obtained the same O(n)-time algorithm by applying Dijkstra’s «standard strategy»;[8] in 1989, Richard Bird derived it by purely algebraic manipulation of the brute-force algorithm using the Bird–Meertens formalism.[9]
Grenander’s two-dimensional generalization can be solved in O(n3) time either by using Kadane’s algorithm as a subroutine, or through a divide-and-conquer approach. Slightly faster algorithms based on distance matrix multiplication have been proposed by Tamaki & Tokuyama (1998) and by Takaoka (2002). There is some evidence that no significantly faster algorithm exists; an algorithm that solves the two-dimensional maximum subarray problem in O(n3−ε) time, for any ε>0, would imply a similarly fast algorithm for the all-pairs shortest paths problem.[10]
Applications[edit]
|
|
This section needs attention from an expert in Computational biology. The specific problem is: fix inline tags. WikiProject Computational biology may be able to help recruit an expert. (September 2019) |
Maximum subarray problems arise in many fields, such as genomic sequence analysis and computer vision.
Genomic sequence analysis employs maximum subarray algorithms to identify important biological segments of protein sequences.[citation needed] These problems include conserved segments, GC-rich regions, tandem repeats, low-complexity filter, DNA binding domains, and regions of high charge.[citation needed]
In computer vision, maximum-subarray algorithms are used on bitmap images to detect the brightest area in an image.
Kadane’s algorithm[edit]
Empty subarrays admitted[edit]
| Example run |
|---|
|
Execution of Kadane’s algorithm on the above example array. Blue: subarray with largest sum ending at i; green: subarray with largest sum encountered so far; a lower case letter indicates an empty array; variable i is left implicit in Python code. |
Kadane’s original algorithm solves the problem version when empty subarrays are admitted. It scans the given array ![{displaystyle A[1ldots n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3d1923568ccfdc916c6cd1c84cb282a32af9074)
In the 

current_sum.[note 3]
Moreover, it computes the subarray with the largest sum anywhere in ![{displaystyle A[1ldots j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f81bf04402d996fbf9efe4c9e68c68d804022adf)
best_sum,[note 4]
and easily obtained as the maximum of all values of current_sum seen so far, cf. line 7 of the algorithm.
As a loop invariant, in the 
current_sum holds the maximum over all 
![{displaystyle A[i]+cdots +A[j-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d953b5c43fc85b567297a449586a6aa761a6c83)
Therefore, current_sum![{displaystyle +A[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f276f74cd74ae67e23c51b1e9ef3764c5798adfd)
is the maximum over all 
![{displaystyle A[i]+cdots +A[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce9a7a1d7259eb0056fc37f9bed9219049cb8cde)

![{displaystyle A[j+1;ldots ;j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7cbec3c9700cbffc27f7452cc996629800229e)
current_sum![{displaystyle +A[j])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/188c430a18abd0a38d9b527d13d3abd631d0d51e)
current_sum, which after that holds the maximum over all 
![{displaystyle A[i]+cdots +A[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce9a7a1d7259eb0056fc37f9bed9219049cb8cde)
Thus, the problem can be solved with the following code,[4][7] expressed here in Python:
def max_subarray(numbers): """Find the largest sum of any contiguous subarray.""" best_sum = 0 current_sum = 0 for x in numbers: current_sum = max(0, current_sum + x) best_sum = max(best_sum, current_sum) return best_sum
This version of the algorithm will return 0 if the input contains no positive elements (including when the input is empty).
The algorithm can be adapted to the case which disallows empty subarrays or to keep track of the starting and ending indices of the maximum subarray.
This algorithm calculates the maximum subarray ending at each position from the maximum subarray ending at the previous position, so it can be viewed as a trivial case of dynamic programming.
No empty subarrays admitted[edit]
For the variant of the problem which disallows empty subarrays, best_sum should be initialized to negative infinity instead[11]
and also in the for loop current_sum should be updated as max(x, current_sum + x).[note 7]
current_sum = max(x, current_sum + x)
In that case, if the input contains no positive element, the returned value is that of the largest element (i.e., the value closest to 0), or negative infinity if the input was empty. For correctness, an exception should be raised when the input array is empty, since an empty array has no maximum nonempty subarray. If the array is non-empty, its first element can be used in place of negative infinity, if needed to avoid mixing numeric and non-numeric values.
Computing the best subarray’s position[edit]
The algorithm can be modified to keep track of the starting and ending indices of the maximum subarray as well.
Because of the way this algorithm uses optimal substructures (the maximum subarray ending at each position is calculated in a simple way from a related but smaller and overlapping subproblem: the maximum subarray ending at the previous position) this algorithm can be viewed as a simple/trivial example of dynamic programming.
Complexity[edit]
The runtime complexity of Kadane’s algorithm is 

Generalizations[edit]
Similar problems may be posed for higher-dimensional arrays, but their solutions are more complicated; see, e.g., Takaoka (2002). Brodal & Jørgensen (2007) showed how to find the k largest subarray sums in a one-dimensional array, in the optimal time bound 
The Maximum sum k-disjoint subarrays can also be computed in the optimal time bound
.[12]
See also[edit]
- Subset sum problem
Notes[edit]
References[edit]
- ^ Bentley 1989, p. 69.
- ^ Bentley 1989, p. 70.
- ^ Bentley 1989, p. 73.
- ^ a b c Bentley 1989, p. 74.
- ^ a b Bentley 1984, p. 868-869.
- ^ Bentley 1989, p. 76-77.
- ^ a b c Gries 1982, p. 211.
- ^ Gries 1982, p. 209-211.
- ^ Bird 1989, Sect.8, p.126.
- ^ Backurs, Dikkala & Tzamos 2016.
- ^ Bentley 1989, p. 78,171.
- ^ Bengtsson & Chen 2007.
- Backurs, Arturs; Dikkala, Nishanth; Tzamos, Christos (2016), «Tight Hardness Results for Maximum Weight Rectangles», Proc. 43rd International Colloquium on Automata, Languages, and Programming: 81:1–81:13, doi:10.4230/LIPIcs.ICALP.2016.81, S2CID 12720136
- Bae, Sung Eun (2007), Sequential and Parallel Algorithms for the Generalized Maximum Subarray Problem (PDF) (Ph.D. thesis), University of Canterbury, S2CID 2681670, archived from the original (PDF) on 2017-10-26.
- Bengtsson, Fredrik; Chen, Jingsen (2007), Computing maximum-scoring segments optimally (PDF) (Research report), Luleå University of Technology
- Bentley, Jon (1984), «Programming Pearls: Algorithm Design Techniques», Communications of the ACM, 27 (9): 865–873, doi:10.1145/358234.381162, S2CID 207565329
- Bentley, Jon (May 1989), Programming Pearls (2nd? ed.), Reading, MA: Addison Wesley, ISBN 0-201-10331-1
- Bird, Richard S. (1989), «Algebraic Identities for Program Calculation» (PDF), The Computer Journal, 32 (2): 122–126, doi:10.1093/comjnl/32.2.122[dead link]
- Brodal, Gerth Stølting; Jørgensen, Allan Grønlund (2007), «A linear time algorithm for the k maximal sums problem», Mathematical Foundations of Computer Science, Lecture Notes in Computer Science, vol. 4708, Springer-Verlag, pp. 442–453, doi:10.1007/978-3-540-74456-6_40.
- Gries, David (1982), «A Note on the Standard Strategy for Developing Loop Invariants and Loops» (PDF), Science of Computer Programming, 2 (3): 207–241, doi:10.1016/0167-6423(83)90015-1, hdl:1813/6370
- Takaoka, Tadao (2002), «Efficient algorithms for the maximum subarray problem by distance matrix multiplication», Electronic Notes in Theoretical Computer Science, 61: 191–200, doi:10.1016/S1571-0661(04)00313-5.
- Tamaki, Hisao; Tokuyama, Takeshi (1998), «Algorithms for the Maximum Subarray Problem Based on Matrix Multiplication», Proceedings of the 9th Symposium on Discrete Algorithms (SODA): 446–452, retrieved November 17, 2018
External links[edit]
- TAN, Lirong. «Maximum Contiguous Subarray Sum Problems» (PDF). Archived from the original (PDF) on 2015-10-10. Retrieved 2017-10-26.
- Mu, Shin-Cheng (2010). «The Maximum Segment Sum Problem: Its Origin, and a Derivation».
- «Notes on Maximum Subarray Problem». 2012.
- www.algorithmist.com
- alexeigor.wikidot.com
- greatest subsequential sum problem on Rosetta Code
- geeksforgeeks page on Kadane’s Algorithm
Далее мы обсудим алгоритм Кадане в Python и его свойство для решения задачи «Максимальная сумма подмассива». Мы узнаем концепцию алгоритма и поработаем над кодом Python для него, используя пример с соответствующими выходными данными. Наконец, мы обсудим временную сложность алгоритма и реальное применение алгоритма Кадане.
Итак, приступим.
Алгоритм Кадане в Python – это один из популярных подходов, используемых для решения проблемы с помощью динамического программирования. Как мы уже знаем, задача определения максимума подмассива считается одной из популярных задач в области динамического программирования.
Проблема кажется простой, и решением должна быть сумма всех элементов данных в массиве. Однако это не так. Мы также встретим отрицательные целые числа как элементы данных в массиве, которые могут уменьшить сумму всего массива. Таким образом, мы воспользуемся помощью алгоритма Кадане для решения этой проблемы.
Алгоритм Кадане используется для поиска непрерывного подмассива в одномерном целочисленном массиве, который имеет максимально возможную сумму. Основным подходом будет применение метода грубой силы для решения проблемы. Однако при этом временная сложность решения будет O (n ^ 2), что совсем не впечатляет.
Следовательно, мы будем использовать алгоритм Кадане для решения задачи путем обхода всего массива с помощью двух переменных, чтобы отслеживать текущую и максимальную сумму. Наиболее важным аспектом, на который следует обращать внимание при использовании этогои алгоритма, является условие, с помощью которого мы будем обновлять обе переменные.
Понимание алгоритма максимальной суммы подмассива
Давайте теперь рассмотрим основные шаги алгоритма максимальной суммы подмассива, как показано ниже:
- Шаг 1: мы должны инициализировать max_till_now = 0.
- Шаг 2: мы должны инициализировать max_ending = 0.
- Шаг 3: мы должны повторить шаги с 4 по 6 для каждого элемента данных в массиве.
- Шаг 4. Мы должны установить max_ending = max_ending + a [i].
- Шаг 5: Если(max_ending <0), мы должны установить max_ending = 0.
- Шаг 6: Если(max_till_now <max_ending), мы должны установить max_till_now = max_ending.
- Шаг 7: мы должны вернуть max_till_now.
Мы использовали max_ending для поиска всех положительных элементов данных массива и max_till_now, чтобы найти максимальную сумму элементов данных среди всех положительных сегментов. Таким образом, каждый раз, когда мы получаем положительную сумму при сравнении с max_till_now, мы сможем обновить ее на большую сумму.
Следовательно, всякий раз, когда max_ending становится отрицательным, мы устанавливаем его равным нулю, и для каждой итерации мы будем проверять условие, при котором max_till_now меньше max_ending, чтобы обновить max_till_now, если условие возвращает True.
Использование графического представления в алгоритме Кадане
Давайте рассмотрим следующий пример с целочисленным массивом.
Рис.1: Целочисленный массив.
Рис. 2. Мы инициализируем max_till_now = 0 и max_ending = 0(n = 0).
Рис. 3. Тогда мы получим max_till_now = 0 и max_ending = 0 для n = 1; однако мы получим max_till_now = 4 и max_ending = 4 для n = 2.
Рис. 4. Затем мы присвоим значение n = 3 и 4 и получим max_till_now = 4 и max_ending = 3, а также max_till_now = 4 и max_ending = 1 соответственно.
Рис. 5. Мы получим max_till_now = 6(6> 4) для n = 5 и max_ending = 6.
Рис. 6: Мы также получим max_till_now = 6 и max_ending = 4 для n = 6.
Следовательно, из приведенного выше примера мы найдем максимальный подмассив в диапазоне от n = 2 до n = 5, а максимальная сумма будет равна 6.
Понимание алгоритма Кадане с использованием кода Python
Давайте рассмотрим следующий фрагмент кода, демонстрирующий работу алгоритма Кадане.
Пример:
# defining the function to find the maximum subarray sum
def max_Subarray_Sum(my_array, array_size):
# assigning the variables
maxTillNow = my_array[0]
maxEnding = 0
# using the for-loop
for n in range(0, array_size):
maxEnding = maxEnding + my_array[n]
# using the if-elif-else statement
if maxEnding < 0:
maxEnding = 0
elif(maxTillNow < maxEnding):
maxTillNow = maxEnding
return maxTillNow
# defining the array
my_array = [-2, -3, 4, -1, -2, 5, -3]
# printing the maximum subarray sum for the users
print("Maximum Subarray Sum:", max_Subarray_Sum(my_array, len(my_array)))
Выход:
Maximum Subarray Sum: 6
Объяснение:
В приведенном выше фрагменте кода мы определили функцию как max_Subarray_Sum, принимающую два параметра как my_array и array_sum соответственно. Затем мы присвоили переменной maxTillNow первому значению индекса массива, а maxEnding – нулю. Затем мы использовали цикл for для перебора всего массива.
Мы также использовали условный оператор if-elif-else и возвращаем maxTillNow. Наконец, мы определили массив и распечатали максимальную сумму подмассивов для пользователей, которая в приведенном выше примере равна 6.
Временная сложность
Временная сложность алгоритма Кадана для массива, состоящего из n элементов данных в виде целого числа, определяется как O(n), поскольку в программе должен выполняться только один цикл for. Аналогично, сложность алгоритма во вспомогательном пространстве равна O(1).
Применение
Существуют различные применения алгоритма Кадане, некоторые из которых описаны ниже:
- Алгоритм Кадане состоит в том, чтобы найти максимальную сумму подмассива для заданного массива целых чисел.
- Он используется в качестве алгоритма обработки изображений.
- Его также можно использовать для решения таких задач, как «Station Travel in Order» и «Hostels Along the Coast».
- Он также используется для бизнес-анализа.
Заключение
Мы можем сделать вывод, что решение не кажется простым при постановке задачи нахождения максимальной суммы подмассива. Однако алгоритм Кадане ее упростил и достиг решения с наименьшими временными сложностями.
Это стало возможным, поскольку алгоритм Кадане использует метод сбора информации, необходимой для достижения решения, избегая нежелательного хранения данных. Следовательно, мы можем рассматривать этот алгоритм как простой пример подхода динамического программирования с множеством практических приложений в реальном мире.

Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Динамическое программирование — способ решения задач путём разбиения их на подзадачи, которые, в свою очередь, используются для нахождения ответа исходной задачи. В этой статье мы разберём несколько классических задач динамического программирования, которые требуют для своего решения одномерный массив, либо, в некоторых случаях, можно даже обойтись без него.
Если вы не знакомы с динамическим программированием, посмотрите эту статью для начинающих.
Числа трибоначчи
Числа трибоначчи — это числовой ряд, начинающийся с трёх чисел 0, 0, 1, где каждое последующее число вычисляется как сумма трёх чисел перед ним:
Рассмотрим следующую задачу: дан массив чисел с порядковыми номерами чисел трибоначчи, например: [73, 10, 4, 15, 20, 7], числа в массиве не превышают 100, требуется вернуть массив, содержащий числа трибоначчи под указанными номерами: [73-е число трибоначчи, 10-е число трибоначчи, и так далее].
Если вы какое-то время работаете с языками программирования, то наверняка решали задачи нахождения факториала или степени числа через рекурсию. Попробуем применить такую же идею здесь:
const tribonacciNumber = (n) => {
// обрабатываем граничные условия, их три,
// т.к. рекурсия будет идти на 3 числа внутрь
if (n === 1 || n === 2) return 0;
if (n === 3) return 1;
return tribonacciNumber(n - 1) +
tribonacciNumber(n - 2) +
tribonacciNumber(n - 3);
}Запускаем функцию с вычислением времени:
console.time();
console.log(tribonacciNumber(36));
console.timeEnd(); // 6337 ms
console.time();
console.log(tribonacciNumber(37));
console.timeEnd(); // 11361 ms
console.time();
console.log(tribonacciNumber(40));
console.timeEnd(); // 71015 ms
console.time();
console.log(tribonacciNumber(41));
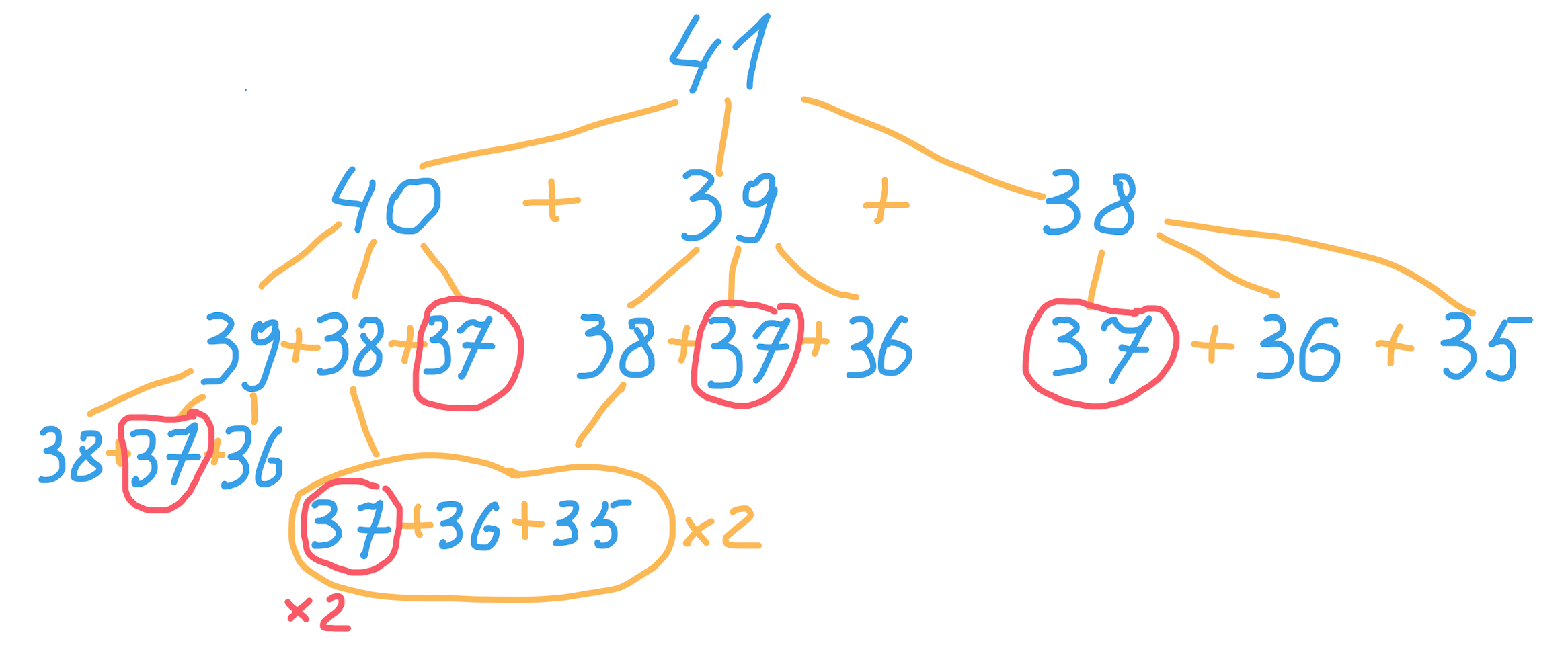
console.timeEnd(); // 135573 ms41-е число вычисляется 135 секунд. Кажется, что быстрее вручную посчитать числа, подставить в массив все 100 значений (ограничение задачи) и просто вернуть число на нужной позиции. В чём же проблема, как так получилось, что простой алгоритм работает так долго? Можно заметить, что следующее число вычисляется в 2 раза дольше, чем предыдущее. Давайте посмотрим на рекурсивное дерево вызовов:
Можно заметить, что при вычислении через рекурсию многие числа будут считаться по несколько раз, например, число 37 будет посчитано 6 раз. В замерах времени выше мы видели, что вычисление этого занимает 11 секунд, т.е. займёт половину времени от вычислений числа 41 — 66 секунд из 135.
Напрашивается решение проблемы — запоминать вычисленные значения и при необходимости просто их использовать. Давайте посмотрим, что получается в таком случае:
// хранит вычисленные числа трибонначи,
// в виде "число трибонначи": "значение числа"
const tribonacciNumbersCache = {};
const tribonacciNumber = (n) => {
if (n === 1 || n === 2) return 0;
if (n === 3) return 1;
// проверяем, было ли вычислено значение числа n
// если да, то просто возвращаем это значение
if (n in tribonacciNumbersCache) {
return tribonacciNumbersCache[n];
}
// вычисляем значения
const nTribonacciNumber = tribonacciNumber(n - 1) +
tribonacciNumber(n - 2) +
tribonacciNumber(n - 3);
// сохраняем вычисленное значение, для переиспользования
tribonacciNumbersCache[n] = nTribonacciNumber;
return nTribonacciNumber;
}Пробуем выполнить новую функция с теми же входными данными:
console.time();
console.log(tribonacciNumber(36));
console.timeEnd(); // 0.26 ms
console.time();
console.log(tribonacciNumber(37));
console.timeEnd(); // 0.11 ms
console.time();
console.log(tribonacciNumber(40));
console.timeEnd(); // 0.10 ms
console.time();
console.log(tribonacciNumber(41));
console.timeEnd(); // 0.09 msВо-первых, мы видим, что выполнение теперь занимает доли миллисекунд. Во-вторых, замечаем понижение времени при каждом новом вызове. Это связано с оптимизациями компилятора JavaScript после определенного количества вызова кода. После пары вызовов время уменьшается на 0.1 миллисекунды (для моего компьютера), следовательно, 100 вычислений, которые нам требуются для исходной задачи, пройдут за 0.01 секунду.
Мы уже применили идеи динамического программирования — сохранили результат вычисления подзадачи для получения результата следующей задачи. Осталось вызвать это в цикле для исходного массива и получить ответ. Но что делать, если в вычисления закрадётся ошибка? Код с рекурсией отлаживать довольно сложно.
Давайте немного упростим решение за счёт идеи предварительного вычисления всех возможных вариантов. Это займёт очень мало времени, т.к. по условию задачи максимальное число — 100, и за счет идеи отказа от рекурсии. Будем считать так, как бы мы считали эти числа на листике, руками:
const tribonacciNumbersCache = [0, 0, 1];
// i < 100, не включая 100, т.к. 100-е число будет находиться в 99 позиции
for (let i = 3; i < 100; i++) {
// используем предыдущие 3 значение из массива, никакой рекурсии
tribonacciNumbersCache.push(tribonacciNumbersCache[i - 1] +
tribonacciNumbersCache[i - 2] +
tribonacciNumbersCache[i - 3])
}Поскольку идем, увеличивая число i, и у нас изначально добавлено в массив tribonacciNumbersCache три значения, то получение элементов i - 1, i - 2 и i - 3 отработает без ошибок.
В 0 позиций массива tribonacciNumbersCache — первое число трибонначи, главное не забыть вычитать единицу при получении значения.
Напишем решение исходной задачи — по массиву номеров получить массив с числами трибонначи:
const tribonacciNumbersCache = [0, 0, 1];
for (let i = 3; i < 100; i++) {
tribonacciNumbersCache.push(tribonacciNumbersCache[i - 1] +
tribonacciNumbersCache[i - 2] +
tribonacciNumbersCache[i - 3])
}
const tribonacciNumbers = [73, 10, 4, 15, 20, 7];
// массив для сохранения самих чисел трибонначи
const tribonacciNumbersValue = [];
for (const number of tribonacciNumbers) {
// просто получаем значения из кеша, не делая никаких вычислений
tribonacciNumbersValue.push(tribonacciNumbersCache[number - 1])
}
console.log(tribonacciNumbersValue);В консоль будет выведено [2073693258389777400, 44, 1, 927, 19513, 7]. Задача решена.
Задачи на LeetCode и CodeWars для тренировки вычислений чисел фибонначи, трибонначи.
Основные идеи
Мы использовали несколько подходов, типичных для динамического программирования:
- Определили, как из известных данных маленьких подзадач будет вычисляться следующая подзадача, т.е. с числами трибонначи из трёх значений будет вычисляться следующее значение. Это соотношение называется рекурсивным.
- Нашли исходные данные, чтобы можно было запустить наше вычисление.
- Определили, откуда брать ответ — вычитали единицу при обращении к элементу массива с посчитанными значениями.
Кузнечик и кувшинки
Рассмотрим следующую задачу: есть определённое количество кувшинок, расположенных в ряд, кузнечик стоит на первой из них. Он может прыгнуть на следующую кувшинку, либо перепрыгнуть через одну. Сколько существует разных способов (путей) добраться до последней кувшинки?
Рассмотрим вариант с 4-мя кувшинками. Можем перебрать варианты и посчитать, что до последней кувшинки можно добраться 3-мя разными способами:
Рассмотрим сколько способов существует, чтобы добраться до каждой из кувшинок. До второй — 1 способ, до третьей — 2 способа: прыгнуть сразу на неё или прыгнуть с первой кувшинки. До четвёртой уже выяснили перебором, что существует 3 способа.
Можем заметить, что на четвёртую кувшинку мы можем прыгнуть только со второй или с третьей и что количество путей до неё равно количеству путей до второй кувшинки + количество путей до третьей кувшинки. Немного порассуждаем, почему так получается.
С третьей кувшинки на четвёртую есть только один путь — прыгнуть на неё, но при этом до третьей кувшинки было 2 разных пути. Соответственно, если мы двигаемся через третью кувшинку на четвёртую, то так и остается 2 разных пути это сделать. Аналогичные рассуждения можно провести для перемещения со второй на четвёртую кувшинку. Эти два случая будут разными путями, т.к. перед попаданием на четвёртой мы были на разных кувшинках, следовательно, количество путей надо просто сложить.
Аналогичные рассуждения можно провести для дальнейших перемещений, т.е. просто складываем количество путей до предыдущих двух кувшинок.
Понятно, как переходить от одной подзадачи к другой, осталось найти начальные условия. Возьмём за начальные условия количество вариантов попасть на вторую и третью кувшинки, т.е. 1 и 2.
Для нахождения начальных условий можно использовать более математический подход: ввести отрицательные кувшинки, количество путей до них будет 0, и использовать текущую позицию как последнее значение начальных условий. При таком подходе начальные условия будут 0 и 1. В текущей задаче будем использовать первый подход, но для более сложных задач имеет смысл использовать второй.
Получается следующая функция:
function getNumberOfWaysJumpingWaterLily(n) {
// количество путей до 1-й и 2-й кувшинки
const jumpWays = [1, 2];
// если n будет 1 или 2, то тело цикла не выполнится ни разу
for (let i = 2; i < n; i++) {
// количество путей до i кувшинки складывается из 2-х путей,
// до предыдущих кувшинок
jumpWays.push(jumpWays[i-1] + jumpWays[i-2]);
}
// в 0 позиции - количество путей до 1-й кувшинки
// в n - 1 позиции - количество путей до n-й кувшинки
return jumpWays[n-1];
}
console.log(getNumberOfWaysJumpingWaterLily(10));Задача решена, но можем заметить, что все значения, кроме двух последних, не используются, и упростить решение:
function getNumberOfWaysJumpingWaterLily(n) {
let way1 = 1;
let way2 = 2;
if (n == 1) return way1;
if (n == 2) return way2;
for (let i = 2; i < n; i++) {
//за счёт деструктуризации массива смещаем значения
[way1, way2] = [way2, way1 + way2];
}
return way2;
};
console.log(getNumberOfWaysJumpingWaterLily(10));
В цикле происходит смещение количества путей до i + 1 кувшинки. В начале way1 указывает на количество путей до первой кувшинки, way2 — до второй. После первого выполнения тела цикла way1 указывает на количество путей до второй кувшинки, way2 до третьей, и так далее. В конце выполнения цикла в way2 получится количество путей до n кувшинки.
Задача для практики на LeetCode
Максимальный(по сумме элементов) подмассив
Условие задачи: дан массив чисел, требуется найти непрерывную последовательность чисел с максимальной суммой.
Например, получен такой массив:
Рассмотрим идею решения. Начнём суммировать значения в этом массиве слева направо. Просуммировав два первых элемента: 2 — 5 = −3, получим отрицательное число. Если добавить это число к следующему, то оно уменьшит его, независимо от того положительное оно или отрицательное. Просуммировав следующие 3 элемента 2 + 2 — 1 = 3, получим положительное значение, которое при добавлении к следующему увеличит сумму с ним в любом случае.
Т.е. мы идём слева направо, суммируя элементы, если сумма становится отрицательной, то игнорируем подсумму, если положительной, то прибавляем дальше:
В процессе этих вычислений при каждом прибавлении сравниваем число с переменной, в которой хранится максимальное подсумма.
Рассмотрим решение в коде:
const maxSubArraySum = (nums) => {
// массив, для хранения подсумм, сразу с одним элементом,
// т.к. в цикле обращаемся к i - 1 элементу
const arrayOfSums = [nums[0]];
// переменная, для хранения максимальных значений
let maxSum = nums[0];
for (let i = 1; i < nums.length; i++) {
// если подсумма, закончившаяся в предыдущем элементе положительная
// то используем её с текущим числом
if (arrayOfSums[i - 1] > 0) {
// добавляем максимальную подсумму, с текущим числом
arrayOfSums.push(arrayOfSums[i - 1] + nums[i]);
} else {
// если предыдущая подсумма отрицательна, то начинаем подсчет заново
arrayOfSums.push(nums[i]);
}
// на текущем шаге учитываем подсумму, заканчивающуюся в i
// предыдущие подсуммы были учтены на предыдущих шагах
if (arrayOfSums[i] > maxSum) {
maxSum = arrayOfSums[i]
}
}
return maxSum;
};
const sourceArray = [2, -5, 2, 2, -1, 3, -1, 2, -5, 4];
console.log(maxSubArraySum(sourceArray));
Рассмотрим массив arrayOfSums, на каждом шаге итерации:
// исходный массив
// [2, -5, 2, 2, -1, 3, -1, 2, -5, 4]
[2, -3]
[2, -3, 2]
[2, -3, 2, 4]
[2, -3, 2, 4, 3]
[2, -3, 2, 4, 3, 6]
[2, -3, 2, 4, 3, 6, 5]
[2, -3, 2, 4, 3, 6, 5, 7]
[2, -3, 2, 4, 3, 6, 5, 7, 2]
[2, -3, 2, 4, 3, 6, 5, 7, 2, 6]Видим, что максимальное значение 7. Это и будет ответ в текущей задаче.
В решении мы находим только максимальную сумму подмассива, но не находим саму часть массива. По рассмотренному массиву arrayOfSums и логике решения задачи довольно очевидно, как найти требуемый подмассив: находим 7 в массиве arrayOfSums, это будет конец подмассива. Берём слева все положительные числа, самое левое из списка положительных чисел — начало подмассива.
В текущем случае это сумма от второго до седьмого элемента (при отсчёте массива от 0). Подмассив arrayOfSums [2, 4, 3, 6, 5, 7], подмассив исходного массива nums [2, 2, -1, 3, -1, 2].
Реализуем эту идею в коде:
const maxSubArray = (nums) => {
const arrayOfSums = [nums[0]];
let maxSum = nums[0];
let maxPosition = 0;
for (let i = 1; i < nums.length; i++) {
if (arrayOfSums[i - 1] > 0) {
arrayOfSums.push(arrayOfSums[i - 1] + nums[i]);
} else {
arrayOfSums.push(nums[i]);
}
if (arrayOfSums[i] > maxSum) {
maxSum = arrayOfSums[i];
maxPosition = i;
}
}
// если максимальная сумма - отрицательная
// значит все элементы в массиве отрицательные
// на каждом шаге сумма вычислялась заново, и arrayOfSums равен nums
// возвращаем максимальное из отрицательных чисел, оно будет в maxPosition
if (maxSum < 0) {
return nums[maxPosition];
}
let endOfMaxSubarray = maxPosition;
// инициализируем startOfMaxSubarray вне for
// т.к. переменная понадобится после выполнения цикла
let startOfMaxSubarray = endOfMaxSubarray;
for (
;
// надо учесть, что можем дойти до начала массива
startOfMaxSubarray >= 0 && arrayOfSums[startOfMaxSubarray] >= 0;
startOfMaxSubarray--
) {}
// i + 1, т.к. цикл завершится на отрицательном элементе
// который не нужно суммировать,
// либо вне границ массива (в -1 позиции)
// endOfMaxSubarray + 1, т.к. последний элемент не включается в slice
return nums.slice(startOfMaxSubarray + 1, endOfMaxSubarray + 1);
};
const sourceArray = [2, -5, 2, 2, -1, 3, -1, 2, -5, 4];
// будет выведено [2, 2, -1, 3, -1, 2]
console.log(maxSubArray(sourceArray));
Задача для практики на LeetCode
Заключение
Мы рассмотрели несколько простых задач динамического программирования, желаю успехов в освоении этого непростого, но очень интересного подхода к решению задач.
Реализации Python и javascript для алгоритмов
Постановка проблемы
У вас есть массив из n чисел. Вам нужно найти наибольшую сумму последовательных чисел массива.
По сути, это поиск подмассива с наибольшей суммой.
Например, массив [1, 2, 3, 4] будет иметь наибольшую сумму = 10, которая является суммой массива в целом. Для массивов без отрицательных целых чисел максимальная сумма подмассива равна сумме самого массива.
Теперь, что происходит, когда у вас есть отрицательные целые числа?
Возьмите массив [-1, -3, 4, 2], где подмассив с максимальной суммой будет [4, 2] с суммой = 6.
Что происходит, когда у вас есть огромный массив? Как разработать алгоритм для решения этой проблемы?
Решение
На самом деле есть много разных способов сделать это. Позвольте мне логически разбить два подхода, чтобы помочь вам понять процесс мышления.
Решение 1
Очень прямой подход, о котором мы можем думать, может выглядеть следующим образом:
- Мы создаем все возможные подмассивы из основного массива.
- Затем мы проверяем сумму каждого подмассива и возвращаем максимальную сумму.
Довольно просто? Давайте сделаем пробный прогон, чтобы понять это лучше.
- Пусть массив будет
[-1, 2, -5, 7] - Чтобы создать все подмассивы этого массива, мы можем выбрать каждый элемент и создать подмассив со всеми остальными элементами в последовательности.
- Вот подмассивы-
[-1], [-1, 2], [-1, -5], [-1, 7], [-1, 2, -5], [-1, 2, 7], [-1, -5, 7], [-1, 2, -5, 7], [2], [2, -5], [2, 7], [2, -5, 7], [-5], [-5, 7], [7].Ах, очень утомительный процесс. - С каждым созданным нами подмассивом мы можем проверить сумму и сохранить ее запись.
- Всякий раз, когда сумма превышает нашу предыдущую запись, мы обновляем значение.
- Как только мы пройдемся по всем подмассивам, записанная нами сумма будет искомым ответом.
- Если мы посмотрим на все подмассивы, то заметим, что
[7, 2]имеет максимальную сумму, которая равна9.
Давайте попробуем сделать это на двух разных языках программирования. Идея состоит не только в том, чтобы решить проблему, но и в том, чтобы изучить синтаксис и код Python и JavaScript. Я предполагаю, что у вас есть общее представление о том, как писать код: циклы for, операторы if-else, объявление переменных и использование функций. Если нет, ознакомьтесь с этими вещами, прежде чем читать код.
У нас слишком много циклов for, а это значит, что временная сложность — это плохо. В данном случае это O(n³), потому что нам нужно выполнить три цикла.
Решение 2
Чтобы сделать вещи эффективными в таких задачах, нам нужно подумать о способах уменьшить количество циклов.
Есть ли способ решить это с помощью одного цикла?
Должен быть какой-то трюк, который мы можем использовать, чтобы сделать это. Посмотрим, сможем ли мы построить мыслительный процесс.
- Если мы перебираем массив только один раз, это означает, что мы посещаем каждый элемент массива один раз.
- Давайте теперь соединим точки в обратном порядке. Чтобы найти наш ответ, нам нужно сначала найти подмассив, который будет иметь максимальную сумму.
- Нам обязательно нужно посетить каждый элемент один раз. Что вы можете сказать об этом элементе по отношению к подмассиву с максимальной суммой? Он либо принадлежит этому подмассиву, либо нет. Правильно?
- Если он принадлежит подмассиву с максимальной суммой, вы можете добавить его значение во временную переменную, где вы сохраняете и постоянно обновляете потенциальную максимальную сумму. Если это не так, вы можете просто проигнорировать его и перейти к следующему элементу.
- Если вы сделаете это по всему массиву, что вы получите? Сумма всех элементов, принадлежащих подмассиву с максимальной суммой = ответ, который мы ищем, и мы получаем его, запустив всего один цикл!
- Теперь у вас возникнет вопрос: как мы узнаем, что данный элемент принадлежит этому подмассиву?
- Предположим, что у нас есть массив из n элементов. Мы находимся в k-м элементе этого массива.
- Если этот k-й элемент является частью нашего максимального подмассива, что в нем будет особенного? Либо она будет больше, чем сумма элементов до
k-1, либо максимальная сумма доk-1+kthэлемента будет больше. - Вы заметили, как мы создаем подзадачу с помощью нашей логики?
- Максимальная сумма подмассива для этого массива, заканчивающегося k-м элементом, фактически является максимальной суммой подмассива массива до k-1-го элемента + k-го элемента (если k-й элемент положителен).
- В любой момент времени мы находим максимальную сумму подмассива для массива до k-го элемента. Когда мы достигнем n-го элемента, мы бы нашли ответ для всего массива.
Звучит запутанно? Ничего страшного. Если вы впервые сталкиваетесь с такой проблемой, это может быть немного сложно. Давайте сделаем пробный прогон с реальным массивом.
- Пусть массив равен
[-1, 2, -5, 7], как в примере, который мы использовали в решении 1. Итак, нам нужно собрать сумму элементов, принадлежащих подмассиву с максимальной суммой (назовем его нашим целевым подмассивом). - Мы запускаем только один цикл. Итак, сначала мы идем к
-1, и это сам по себе подмассив с суммой =-1. Предположим, что-1является частью нашего целевого подмассива.-1теперь наша временная максимальная сумма. - Далее идем к
2. Теперь он либо является частью нашего целевого подмассива, либо нет. Откуда мы это знаем? Если он является частью подмассива, он должен быть либо больше текущей максимальной суммы, либо должен быть добавлен к максимальной сумме.2 > -1 + 2 = 1, что больше, чем наша текущая временная максимальная сумма. Итак, давайте обновим нашу временную максимальную сумму =2. Это просто подтверждает, что наше предыдущее предположение о том, что-1является частью целевого массива, неверно. Теперь предположим, что2является частью целевого массива. - Давайте перейдем к следующему элементу, то есть
-5.-5явно меньше текущей максимальной суммы, которую мы имеем. Таким образом, мы можем игнорировать его и перейти к следующему элементу. - Теперь давайте перейдем к следующему элементу,
7, который больше, чем текущая максимальная сумма =2.7 + 2 = 9, что также больше, чем наша текущая максимальная сумма. Это означает, что7является частью нашего целевого подмассива, и мы можем обновить нашу максимальную сумму =9. - Мы достигли конца массива, и решение, к которому мы пришли, это
9, что является требуемым ответом, и мы только что использовали один цикл!
Короче говоря, мы подошли к каждому элементу массива и проверили, будет ли он частью подмассива с максимальной суммой. Если это так, мы просто добавляем его в нашу переменную maxSum и переходим к следующему элементу.
В конце мы получим требуемый ответ.
Вот реализация кода в javascript и python для этого подхода:
Поскольку мы используем только один цикл, временная сложность равна O(n).
Некоторые наблюдения
- Я запустил обе эти программы в Leetcode для соответствующего вопроса (решение 2).
- Программа javascript выполнялась меньше времени, чем код python.
- Однако python занимал меньше памяти, чем javascript.
Ключевые выводы
- Если вы столкнетесь с похожей проблемой на собеседовании, подумайте о том, как вы пытаетесь найти решение.
- Возьмите образец тестового примера и выполните пробный прогон, как я сделал здесь в первую очередь.
- И после этого вы можете кодировать его.
- Если вы столкнулись с такой проблемой в онлайн-тестировании, использование javascript вместо python может помочь вам занять более высокое место в рейтинге, поскольку он быстрее.
- Когда вы имеете дело с массивами и замечаете, что вам нужно выполнить итерацию по массиву, вам следует подумать об использовании наименьшего количества циклов for.
- Оттуда подумайте о том, что вы можете сделать, как вы можете отслеживать полезную информацию, проходя через каждый элемент массива.
- В таких задачах мы обычно хотели бы отслеживать две переменные: текущее значение, которое мы вычисляем на каждой итерации, и максимальное или минимальное значение, которое будет окончательным ответом, который постоянно обновляется по мере прохождения массива.
Fundamental Approach: A summary. 1. Have a single for loop. 2. Calculate a currentValue for each element in the array based on the question. 3. Then update the maxValue as max(maxValue, currentValue) 4. Vice-versa for minValue.
Попробуйте решить этот вопрос Leetcode самостоятельно, не видя никаких ссылок после прочтения этой статьи, и проверьте свое понимание.
После этого попробуйте эту задачу, которая не так проста, но может быть решена с использованием фундаментальной логики и мыслительного процесса, которые мы здесь исследовали.

![{displaystyle sum _{x=i}^{j}A[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f4ae4590a685044ab6ba7cc8b23cc7c57f5689e)