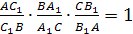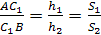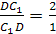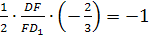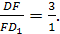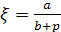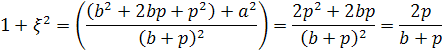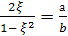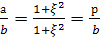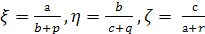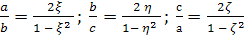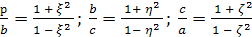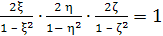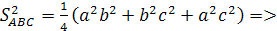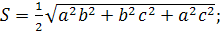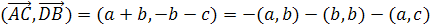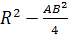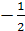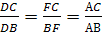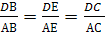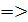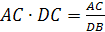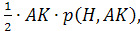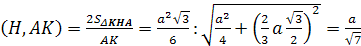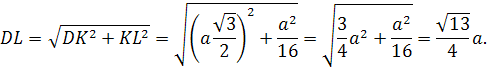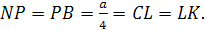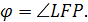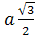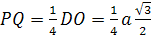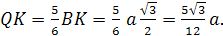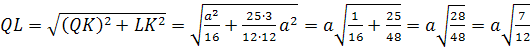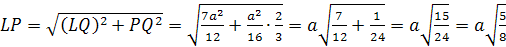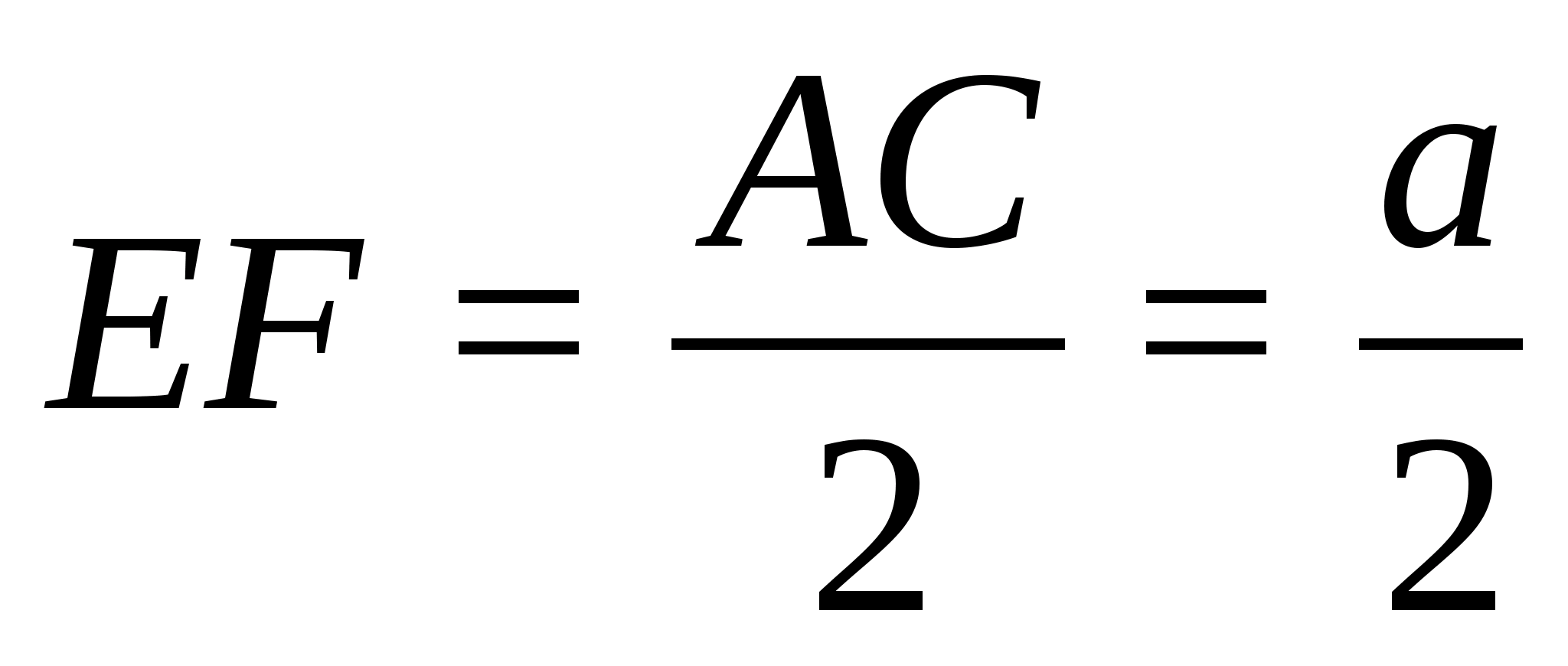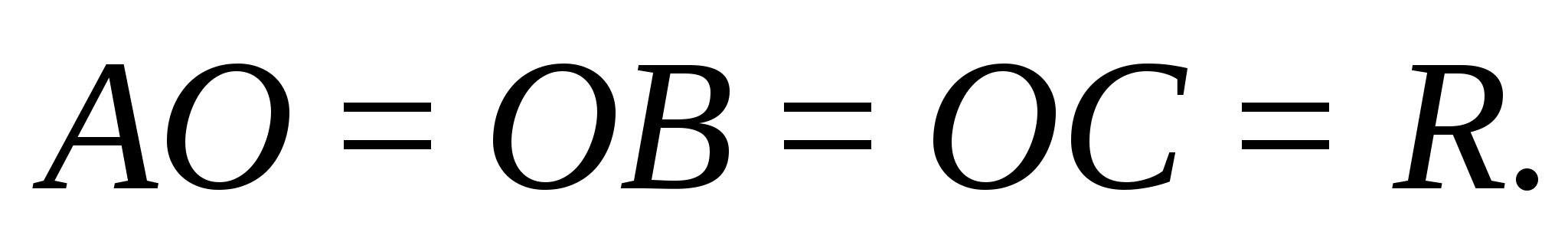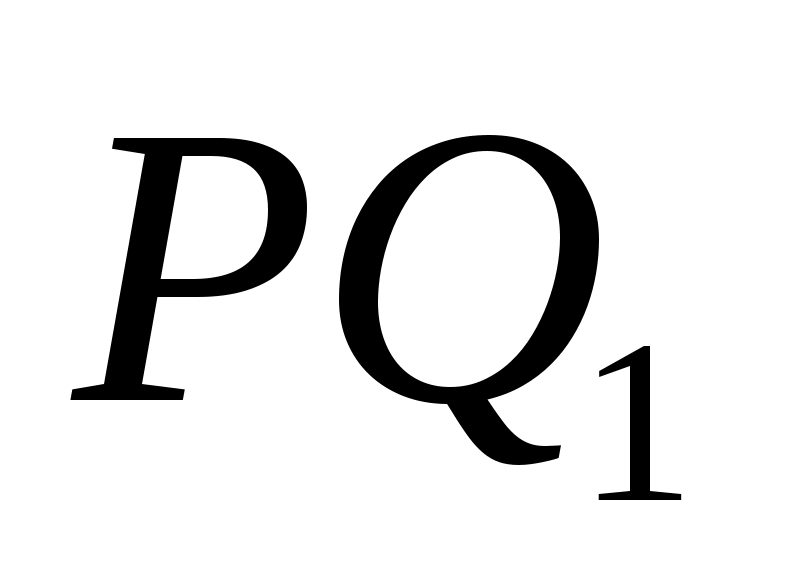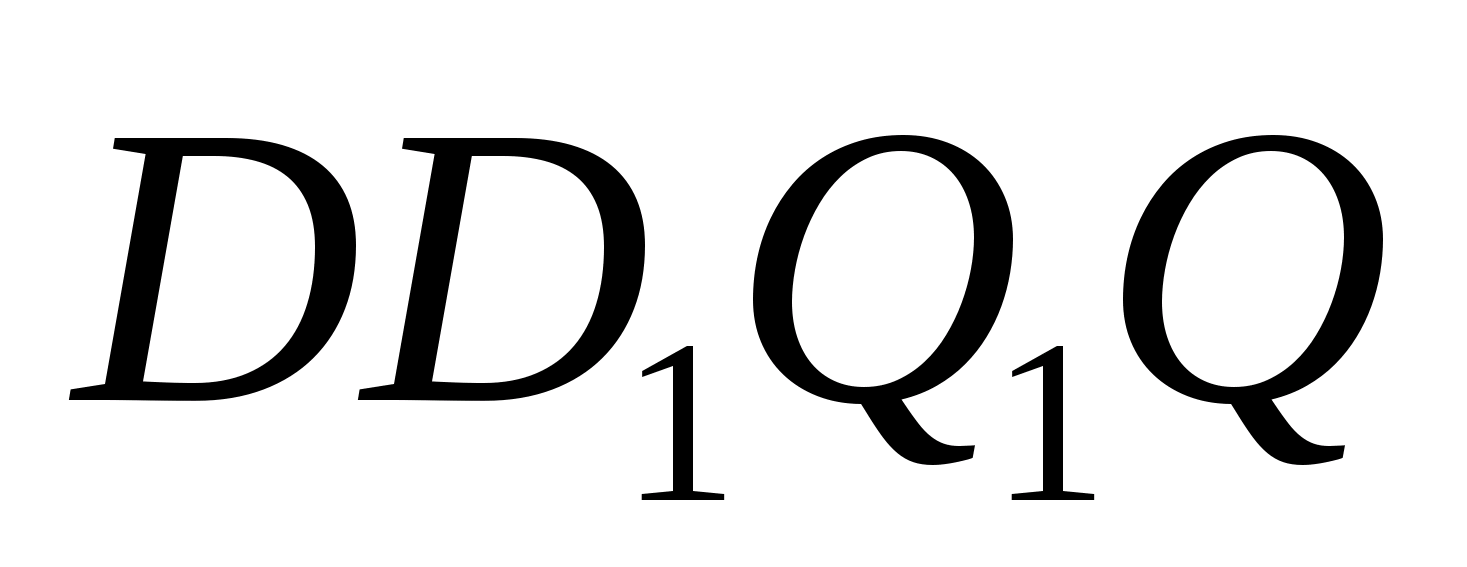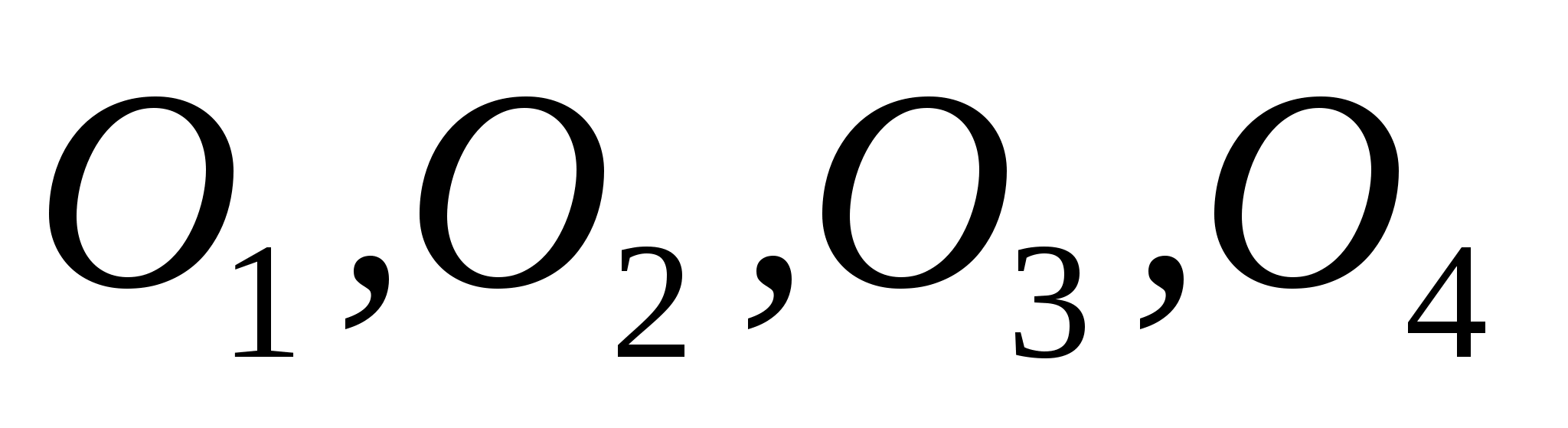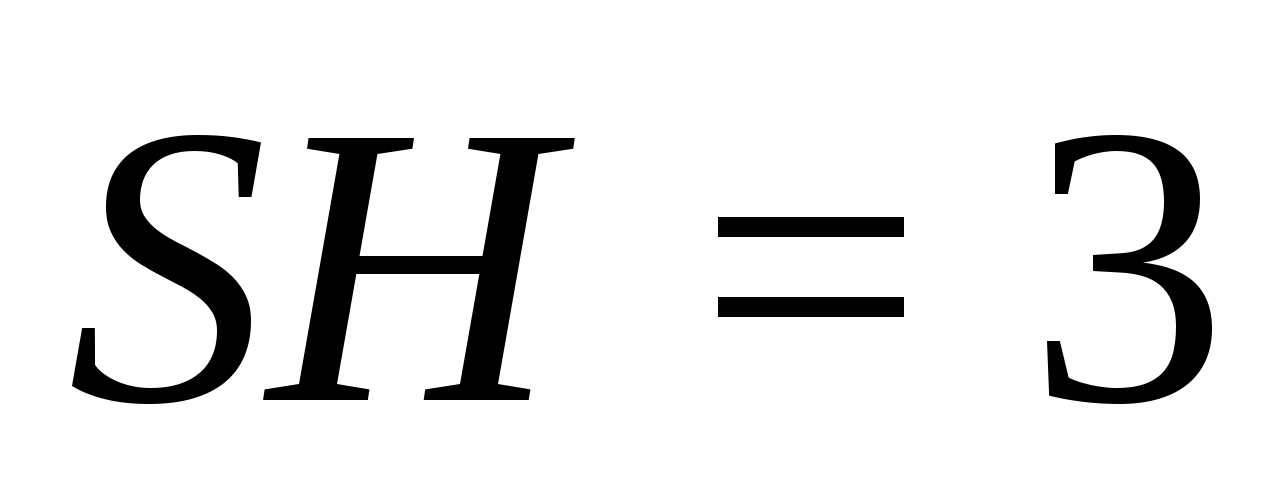Доказательство подобия треугольников в тетраэдре
ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ
Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
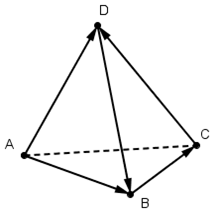
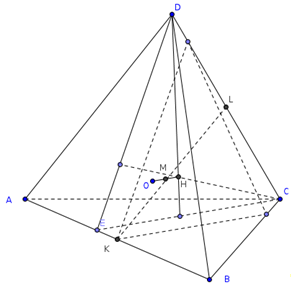
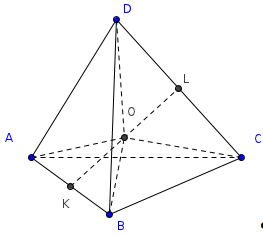
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.
Теорема 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности.
Теорема 2′. Плоскости, проходящие через середины ребер тетраэдра и перпендикулярные этим ребрам, пересекаются в одной точке – центре описанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением плоскостей, проходящих через середины ребер AD, BD, и CD является точка O, равноудаленная от всех вершин тетраэдра. Следовательно, эта точка принадлежит остальным плоскостям и является центром описанной сферы.
Теорема 2″. Прямые, перпендикулярные граням тетраэдра, и проходящие через центры их описанных окружностей, пересекаются в одной точке – центре описанной сферы.
Доказательство. Каждая такая прямая является геометрическим местом точек, равноудаленных от вершин соответствующей грани тетраэдра. Поэтому центр описанной сферы будет принадлежать всем этим прямым.
Заметим, что не у всякого тетраэдра прямые, проходящие через центры вписанных в грани окружностей и перпендикулярные этим граням, пересекаются в одной точке. Ответ на то, когда это происходит, дает следующая теорема.
Теорема 2»’. У тетраэдра существует сфера, касающаяся всех его ребер, тогда и только тогда, когда суммы противоположных ребер этого тетраэдра равны.
Доказательство. Пусть у тетраэдра ABCD существует сфера, касающаяся его ребер. Обозначим через a, b, c и d расстояния от соответствующих вершин тетраэдра до точек касания. Тогда AB = a + b, CD = c + d. Следовательно, AB + CD = a + b + c + d. Аналогично, AC + BD = a + b + c + d, AD + BC = a + b + c + d. Таким образом, суммы противоположных ребер тетраэдра равны.
Обратно. Предположим, что суммы противоположных ребер тетраэдра ABCD равны. Впишем в треугольник ABC окружность. Обозначим через X точку касания этой окружности стороны AB (рис. 2) .
Тогда AX = (AB + AC – BC):2. Так как AC – BC = AD – BD, то AX = (AB + AD – BD):2. Следовательно, точка X является точкой касания окружности, вписанной в треугольник ABD . Через центры этих двух окружностей проведем перпендикуляры. Они лежат в одной плоскости, проходящей через X и перпендикулярной AB. Точка O их пересечения будет равноудалена от сторон треугольников ABC и ABD. Таким образом, любые два перпендикуляра, проходящие через центры окружностей, вписанных в грани тетраэдра, пересекаются. Из этого следует, что или они лежат в одной плоскости, или пересекаются в одной точке. Поскольку они не лежат в одной плоскости, то значит, они пересекаются в одной точке O , равноудаленной от всех ребер тетраэдра, т.е. O – центр сферы, касающейся всех ребер данного тетраэдра.
Теорема 3. Медианы треугольника пересекаются в одной точке, называемой центроидом треугольника и делятся в этой точке в отношениии 2 : 1.
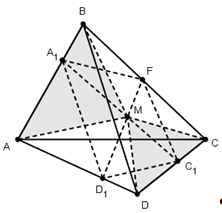
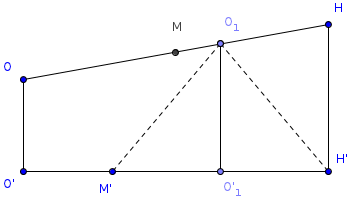
Теорема 3′. Отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противоположных граней, пересекаются в одной точке – центроиде тетраэдра и делятся в этой точке в отношении 3 : 1, считая от вершины.
Доказательство. Пусть ABCD – тетраэдр, O – точка пересечения медиан треугольника ABC, P – точка пересечения медиан треугольника BCD, R – точка пересечения отрезков DO и AP (рис. 3) .
Рассмотрим треугольник AQD. Точки O и P делят соответствующие стороны в отношении 2 : 1. Покажем, что точка R делит DO и AP в отношении 3 : 1. В треугольнике APQ проведем OS параллельно AP. Она разделит отрезок PQ в отношении 2 : 1. Если отрезок SQ принять за единицу, то отрезок DP будет равен 6. Отрезки DR и RQ относятся также как DP и PS, т.е. DR : RQ = 6 : 2 = 3 : 1. Аналогичным образом доказывается, что точка R делит отрезок AP в отношении 3 : 1. Отрезки, соединяющие вершины B и C с точками пересечения медиан противоположных граней также будут делить отрезок DO в отношении 3 : 1 и, следовательно, будут проходить через точку O . Что и требовалось доказать.
Теорема 4. Отрезки, соединяющие середины противоположных ребер тетраэдр, пересекаются в одной точке – центроиде.
Доказательство. Достаточно заметить, что в предыдущем доказательстве медиана треугольника AQD, проведенная из вершины Q, проходит через центроид O .
Теорема 5. Для цетроида O треугольника ABC имеет место равенство .
Теорема 5′. Для цетроида O тетраэдра ABCD имеет место равенство .
Теорема 6. Пусть a произвольная прямая, проходящая через центроид треугольника ABC. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна нулю.
Теорема 6′. Пусть произвольная плоскость, проходящая через центроид тетраэдра ABCD. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна нулю.
Теорема 7. Пусть a произвольная прямая. Будем считать одну из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a, взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина, равна утроенному расстоянию от центроида треугольника до прямой a .
Теорема 7′. Пусть a произвольная плоскость. Будем считать одно из полупространств, на которые эта плоскость разбивает пространство, положительным, а другое отрицательным. Тогда сумма расстояний от вершин тетраэдра до плоскости a , взятых со знаком + или – в зависимости от того, какому полупространству принадлежит вершина, равна учетверенному расстоянию от центроида тетраэдра до данной плоскости.
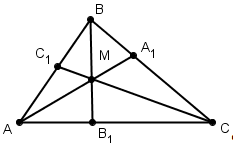
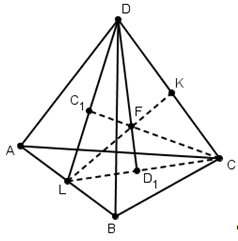
Теорема 8′ (Менелая). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A 1 , B 1 , C 1 и D 1 . Для того чтобы эти точки лежали в одной плоскости, необходимо и достаточно, чтобы выполнялось равенство
Доказательство. Пусть точки A 1 , B 1 , C 1 и D 1 лежат в одной плоскости (рис. 4). Опустим из вершин тетраэдра перпендикуляры AA ’ , BB ’ , CC ’ , DD ’ на эту плоскость. Тогда AA 1 : A 1 B = AA ’ : BB ’ , BB 1 : B 1 C = BB ’ : CC ’ , CC 1 : C 1 D = CC ’ : DD ’ , DD 1 : D 1 A = DD ’ : AA ’ . Откуда и следует требуемое равенство.
Обратно, пусть выполняется указанное равенство. Через точки A 1 , B 1 , C 1 проведем плоскость. Она пересечет ребро AD в некоторой точке D ’ . Для точек A 1 , B 1 , C 1 и D ’ также выполняется указанное равенство. Из этого следует, что DD 1 : D 1 A = DD ’ : D ’ A и, значит, D 1 и D ’ совпадают, т.е. A 1 , B 1 , C 1 и D 1 лежат в одной плоскости.
Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A 1 , B 1 , C 1 и D 1. Плоскости ABC 1 , BCD 1 , CDA 1 и DAB 1 пересекаются в одной точке тогда и только тогда, когда
Доказательство. По предыдущей теореме выполнимость указанного равенства равносильна тому, что точки A 1 , B 1 , C 1 и D 1 лежат в одной плоскости. При этом точка пересечения этих плоскостей является точкой пересечения диагоналей четырехугольника A 1 B 1 C 1 D 1 .
Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
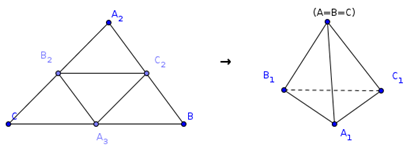
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).
Они образуют треугольник A 1 B 1 C 1 , разбитый на четыре треугольника, равных исходному. Ясно, что A 1 B 1 C 1 представляет собой развертку равногранного тетраэдра.
Теорема 11. Тетраэдр является равногранным тогда и только тогда, когда у него центры вписанной и описанной сфер совпадают.
Доказательство. Пусть в тетраэдре ABCD центрами вписанной и описанной сфер является точка O . P и Q – и точки касания вписанной сферы граней ABC и BCD (рис.6) . Заметим, что P и Q являются центрами окружностей, описанных около треугольников ABC и BCD соответственно. Из этого, в частности, следует, что треугольник ABC – остроугольный. Кроме того, треугольники BP C и BQ C равны. Углы BAC и BDC равны половинам углов BP C и BQ C , и следовательно также равны. Таким образом, плоские углы при вершине D равны углам треугольника ABC. Значит, в сумме они составляют 180 0 . Аналогично, плоские углы при остальных вершинах тетраэдра в сумме составляют 180 0 . Поэтому развертка этого тетраэдра имеет вид, указанный в теореме 1. Следовательно, тетраэдр равногранный.
Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .
Мы рассмотрим другой способ. Имеем S ADB = S ABC cos ; S ACD = S ABC cos ; S BCD = S ABC cos , где , , — соответствующие двугранные углы, равные углам C DO, BDO и A DO . Таким образом, cos , cos , cos составляют координаты единичного вектора, поэтому cos 2 + cos 2 + cos 2 = 1. Значит , S 2 ABC = S 2 ABD + S 2 BCD + S 2 ACD . Что и требовалось доказать.
Ортогональным называется тетраэдр, у которого противоположные ребра попарно перпендикулярны.
Ортоцентрическим называется тетраэдр, у которого высоты или их продолжения пересекаются в одной точке – ортоцентре третаэдра.
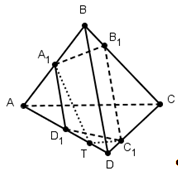
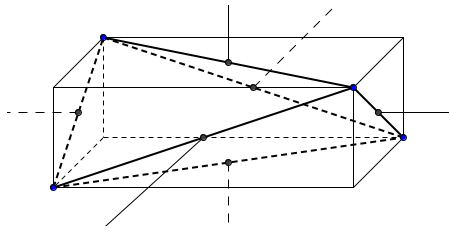
Теорема 14. Тетраэдр является ортогональным тогда и только тогда, когда отрезки, соединяющие середины противоположных ребер, равны.
Доказательство. Пусть ABCD – тетраэдр. A 1 , B 1, C 1, D 1 – середины двух пар противоположных ребер (рис. 8).
Тогда A 1 B 1 D 1 C 1 – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC BD .
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD 2 – высота, опущенная из вершины D. Плоскость CDD 2 перпендикулярна AB и, следовательно, DC 1 и CC 1 – высоты треугольников ABC и ABD. Высоты DD 2 и CC 2 треугольника C 1 CD пересекаются.
Таким образом, произвольные пары высот тетраэдра пересекаются в одной точке. Но попарно пересекающиеся прямые или лежат в одной плоскости, или пересекаются в одной точке. В нашем случае прямые не лежат в одной плоскости и, следовательно, пересекаются в одной точке O .
Обратно, пусть высоты тетраэдра ABCD пересекаются в одной точке O. Тогда DD 2 ABC и, следовательно, DD 2 ABC . Аналогично, CC 2 ABD и, следовательно, CC 2 AB . Таким образом, AB перпендикулярна плоскости COD и, следовательно, AB CD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 3. Тетраэдр является ортогональным тогда и только тогда, когда одна из его высот проходит через ортоцентр соответствующей грани.
Доказательство. Необходимость вытекает из Теоремы 2. Покажем достаточность. Пусть D 2 – ортоцентр грани ABC, DD 2 – высота тетраэдра ABCD. Тогда BC перпендикулярна плоскости AA 1 D и, следовательно, BC перпендикулярна AD. Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 4. В ортогональном тетраэдре окружности 9-ти точек всех граней лежат на одной сфере (сфера 24 точек).
Доказательство. Рассмотрим сферу с центром в центроиде тетраэдра и диаметром, равным отрезкам, соединяющим середины противоположных ребер. Эта сфера проходит через середины всех ребер тетраэдра и, следовательно, содержит окружности 9 точек всех граней.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.
Подобные треугольники — признаки, свойства и теоремы
Общие сведения
Специалисты рекомендуют начинать любое обучение с азов. Следует применять принцип, который называется «от простого к сложному». В плоскостной геометрии (Евклида) существует два понятия: аксиомы и теоремы. К первым относятся утверждения, не требующие доказательства. Они являются базовыми элементами науки и позволяют доказывать другие гипотезы или утверждения.
Кроме того, на основании доказанных гипотез можно производить операции по доказательству более сложных теорем. Иными словами, геометрия состоит из базисных элементов — аксиом, при использовании которых можно преобразовывать утверждения в неоспоримые факты, а также при комбинациях появляется возможность доказательства более сложных (составных) элементов. Примером последнего случая является гипотеза Пифагора для прямоугольного треугольника. Чтобы ее доказать, нужно знать аксиомы геометрии, а также теорему об отношении площадей подобных треугольников (S/S’). Далее необходимо разобрать основные объекты геометрии.
Объекты геометрии
Простейшим объектом геометрии является точка. С помощью нее строятся простые фигуры, благодаря которым образуются более сложные формы. К элементарным компонентам можно отнести следующие: прямая, отрезок, луч. Первая состоит из множества точек, соединенных между собой в одной плоскости и находящихся в поперечном сечении, диаметр которого эквивалентен диаметру точек. При соединении простейших объектов получается бесконечная линия без перегибов.
Лучом называется часть прямой, имеющая начальную точку, но у которой нет конечной границы. Еще существует один элемент, у которого присутствуют обе границы (левая и правая). Он называется отрезком. Следует отметить, что луч и отрезок могут лежать на одной прямой, а также последний может являться частью первого.
При комбинации двух лучей, исходящих из одной точки получается плоский угол. Он измеряется в градусах или радианах. Следует отметить, что в геометрии существует понятие «нулевого» угла. Это возможно, когда лучи совпадают. При комбинации трех углов можно получить треугольник. Существует также другое определение этой фигуры: треугольником (Δ) называется фигура, состоящая из трех точек, одна из которых не лежит на одной прямой с остальными.
Треугольники бывают разносторонними, равнобедренными и равносторонними. Кроме того, в зависимости от градусной меры, они делятся на такие классы: остроугольные, тупоугольные и прямоугольные. Необходимо также отметить, что сумма углов этой геометрической фигуры эквивалентна 180 градусам.
Нужно обратить внимание на такие термины: высоту, медиану и биссектрису. Первой называется перпендикуляр, проведенный из вершины к противоположной стороне. Медиана — отрезок, проведенный из противоположной вершины к середине стороны. Биссектрисой угла является луч или отрезок, который делит его на два равнозначных по величине. В равнобедренном и равностороннем Δ эти элементы совпадают.
Основные аксиомы Евклида
Аксиомой называется утверждение, не требующее доказательств и воспринимаемое в виде факта. Существуют следующие утверждения, которые можно применять при решении задач:
- Если на плоскости существует некоторая прямая, то в этом случае точки классифицируются на две группы по отношению к ней: лежащие и не лежащие.
- Через две точки можно провести только одну прямую.
- При заданных прямой и точке, не лежащей на ней, через последнюю можно провести только одну прямую, которая будет параллельна (||) исходной.
- Когда даны три угла, один из которых эквивалентен другому, а последний — третьему, тогда можно сделать вывод об их равенстве. Аналогичное утверждение существует и для отрезков.
- Любая прямая содержит две точки, а также точку, лежащую между ними.
- Точки, находящиеся на одной плоскости, могут соединяться в любой последовательности вспомогательными отрезками.
Следует обратить внимание на последнюю аксиому. Она позволяет строить любые фигуры на плоскости и в пространстве. Математики очень часто применяют такой прием при решении задач и доказательстве некоторых тождеств при помощи создания дополнительных элементов на чертеже.
Например, в некотором упражнении по нахождению отдельных параметров треугольника в условии содержится очень мало данных. Последний можно вписать в окружность или дополнить до квадрата или прямоугольника. Далее следует разобраться в признаках подобия треугольников.
Подобие двух треугольников
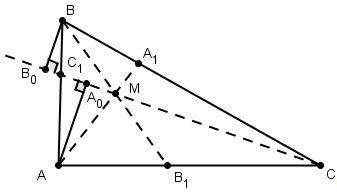
Треугольники являются подобными, когда углы одного эквивалентны всем градусным мерам углов другого, а стороны одного равны сторонам другого, с учетом коэффициента гомотетии. Последний называют еще коэффициентом подобия. Он равен отношению сторон подобных треугольников. Например, дано два подобных Δ ABC и A’B’C’ (больший). Коэффициент подобия треугольников обозначается литерой «k». Он больше 0 и вычисляется по такой формуле: k = A’B’ / AB = B’C’ / BC = A’C’ / AC. Подобие фигур обозначается таким образом: ΔABC ∼ ΔA’B’C’.
Не во всех случаях бывают известны углы и стороны фигур. Для этого были сформулированы три признака (условия или критерия), по которым можно определить подобие.
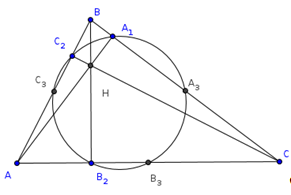
Первое условие
Формулировка первого признака подобия треугольников гласит, что равенство двух углов между собой соответствует подобию двух фигур. Подробнее исходные данные записываются в таком виде: ΔABC ∼ ΔA’B’C’, когда ∠ВАС = ∠B’A’C’ и ∠ABC = ∠A’B’C’. Доказать утверждение довольно просто. Для этого следует рассчитать третий угол у треугольников исходя из того, что сумма трех углов составляет 180 градусов.
Далее необходимо наложить один Δ на другой, чтобы ∠ВАС совпал с ∠B’A’C’. Используя теорему Фалеса для сторон угла, которые делят на отрезки AC / A’C’ = BC / B’C’ вершины малого Δ на пропорциональные части. Аналогично доказывается пропорциональность для двух других сторон. Однако для этого следует наложить уже треугольники таким образом, чтобы совпали другие углы. Такие же действия проделать и для третьего угла. На основании определения о подобии треугольников утверждение доказано. Из доказательства математики получили некоторые следствия, которые будут очень полезны при решении задач:
- Фигуры (Δ) подобны при параллельности 3 сторон одного Δ сторонам другого, при перпендикулярности одно стороны другой, а также отсутствия || двух сторон одного Δ сторонам другого.
- Фигура, полученная при помощи параллельного переноса со сторонами, которые умножаются на некоторый постоянный коэффициент, подобна исходной.
Равенство AC / A’C’ = BC / B’C’ эквивалентно коэффициенту подобия. Этот факт можно использовать при решении задач и доказательства других геометрических утверждений или тождеств.
Второй критерий
Математики выделяют еще один признак подобия треугольников по двум пропорциональным сторонам и углу между ними. Для доказательства следует рассмотреть ΔABC и ΔA’B’C’ со сторонами, связанными таким тождеством: AB / A’B’ = AC / A’C’. Кроме того, углы между ними равны: ∠ВАС = ∠B’A’C’. Далее нужно достроить ΔABC до четырехугольника ABCС». Вершина С» должна располагаться в зеркальном отображении относительно стороны AB. Полученный ΔABC» ∼ ΔA’B’C’ по I признаку, поскольку у них два угла равны. Следовательно, тождество можно править таким образом: AB / A’B’ = AC» / A’C’.
По условию должно выполняться условие AB / A’B’ = AC / A’C’. Тогда AC = AC». На основании этого факта можно сделать вывод о равенстве ΔABC и ΔABC». Следовательно, теорема доказана, поскольку эти треугольники (ΔABC» и ΔA’B’C’) подобны по I признаку.
Третий признак
Третий признак подобия двух треугольников формулируется таким образом: два треугольника являются подобными, когда стороны одного пропорциональны сторонам другой фигуры. Для доказательства необходимо рассмотреть ΔABC и ΔA’B’C’ со сторонами: AB / A’B’ = AC / A’C’ = BC / B’C’.
Математики рекомендуют отметить некоторую точку C» относительно стороны AB. Она не должна лежать на последней. Кроме того, расстояния от C и C» до стороны AB должны быть эквивалентны. Иными словами, следует построить ΔABС», который является «зеркальным» отображением ΔABC относительно его стороны AB. Если AB / A’B’ = AC» / A’C’, то ΔABC» ∼ ΔA’B’C’ по I признаку.
Следующий шаг — доказательство равенства ΔABC и ΔABC». Они равны по двум сторонам AC = AC» и BC = BC». Следовательно, ΔABC ∼ ΔA’B’C’ подобные.
Теорема об отношении площадей
Для решения задач специалисты рекомендуют применять еще теорему об отношении площадей. Обязательным условием ее использования являются ΔABC ∼ ΔA’B’C’ с коэффициентом подобия «k». Ее формулировка имеет такой вид: величина отношения площадей двух подобных треугольников прямо пропорциональна квадрату гомотетии.
Исходя из равенства углов ∠ВАС = ∠B’A’C’ можно записать такое соотношение, в котором тригонометрическая функция не учитывается, поскольку при делении равных коэффициентов получается 1: S / S’ = (AB * AC) / (A’B’ * A’C’). По свойству произведения дробей верно такое преобразование: (AB / A’B’) * (AC / A’C’) = k * k = k 2 . Утверждение доказано полностью.
Некоторые свойства и следствия
Математики также считают, что используя некоторые свойства и следствия из теорем, можно расширить возможности по решению задач. Свойства подобных треугольников можно применять и к другим плоским или объемным фигурам. Следствия классифицируются на несколько типов:
- Отношение площадей плоских фигур прямо пропорционально квадрату их k.
- Куб коэффициента подобия прямо пропорционален объему большей фигуры и обратно пропорционален объему меньшей: V / V’ = k 3 .
- Коэффициент «k» эквивалентен отношению периметров (P), а также биссектрис, медиан, высот и перпендикуляров, которые являются серединными.
- В прямоугольном Δ длина высоты, опущенной на гипотенузу, эквивалентна среднему геометрическому двух проекций на соответствующий катет. Если она опущена из прямого ∠, то значит делит фигуру на подобные Δ по I признаку.
- Величина катета эквивалентна средней величине в геометрической интерпретации гипотенузы и произведению проекции катета на гипотенузу.
Например, второе свойство можно применить для решения такого упражнения: дан объем большего конуса V = 125 м 3 , а необходимо найти значение V’ для малого, зная коэффициент k, который равен 3. Задача решается очень просто: V’ = [V]^(1/3) = [125]^(1/3) = 5 (м 3 ).
Пример решения
Существуют множество типов задач, однако наиболее часто попадаются такие, в которых необходимо доказать, что фигуры являются подобными. Стороны ΔABC равны таким значениям: 10, 12 и 25. Кроме того, существует еще ΔA’B’C’ со сторонами 5, 6 и 10. Фигуры не имеют точек пересечения. Необходимо доказать их подобие.
Для решения рисунок чертить необязательно, поскольку для доказательства необходимо применение не геометрического метода, а алгебраического. Следует ввести обозначения для ΔABC: AB = 10, BC = 12 и AC = 25. Аналогичную процедуру необходимо сделать для ΔA’B’C’: сторона A’B’ равна числу 5, B’C’ = 6 и A’C’ = 10.
Далее нужно вычислить коэффициент k для каждой из сторон: k1 = AB / A’B’ = 10 / 5 = 2, k2 = BC / B’C’ = 12 / 6 = 2 и k3 = AC / A’C’ = 25 / 10 = 2,5. Из соотношений следует, что фигуры не являются подобными, поскольку не выполняется такое равенство: k = k1 = k2 = k3. Для наглядности можно построить также таблицу со значениями коэффициентов.
Таким образом, для решения задач по нахождению параметров подобных треугольников необходимо знать признаки подобия, а также некоторые свойства, которые рекомендуют использовать специалисты-математики.
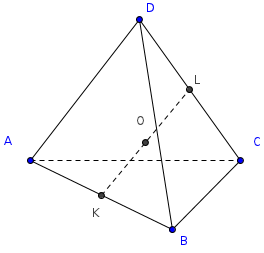
В тетраэдре DABC точки В1, С1 и D1 — середины ребер АВ, АС и AD соответственно. а) Докажите подобие треугольников B1
Ваш ответ
Похожие вопросы
- Все категории
- экономические 43,287
- гуманитарные 33,620
- юридические 17,900
- школьный раздел 607,113
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
http://nauka.club/matematika/geometriya/podobny%D0%B5-treugolniki.html
http://www.soloby.ru/1214339/%D1%82%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80%D0%B5-%D1%81%D0%B5%D1%80%D0%B5%D0%B4%D0%B8%D0%BD%D1%8B-%D1%81%D0%BE%D0%BE%D1%82%D0%B2%D0%B5%D1%82%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%BE-%D0%B4%D0%BE%D0%BA%D0%B0%D0%B6%D0%B8%D1%82%D0%B5-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2
Ответ:
11 см²
Объяснение:
Точки А₁, В₁ и С₁ середины ребер тетраэдра, значит
А₁В₁ — средняя линия ΔDAB и А₁В₁ = 1/2 АВ,
А₁С₁ — средняя линия ΔDAС и А₁С₁ = 1/2 АС,
В₁С₁ — средняя линия ΔDВС и В₁С₁ = 1/2 ВС,
Т.е. стороны треугольника А₁В₁С₁ пропорциональны сторонам треугольника АВС, значит
ΔА₁В₁С₁ подобен ΔАВС по трем пропорциональным сторонам.
Коэффициент подобия:
k = A₁B₁ / AB = 1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sa₁b₁c₁ / Sabc = k² = 1/4
Sa₁b₁c₁ = Sabc / 4 = 44 / 4 = 11 см²
UCHEES.RU — помощь студентам и школьникам
В 14:16 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
В тетраэдре DABC точки В1, С1 и D1 — середины ребер АВ, АС и AD соответственно.
а) Докажите подобие треугольников B1C1D1 и BCD.
б) Найдите площадь треугольника BCD, если площадь треугольника B1C1Dl равна 12 см2.
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: В тетраэдре DABC точки В1, С1 и D1 — середины ребер АВ, АС и AD соответственно.
а) Докажите подобие треугольников B1C1D1 и BCD.
б) Найдите площадь треугольника BCD, если площадь треугольника B1C1Dl равна 12 см2.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Полякова Гелана Рудольфовна — автор студенческих работ, заработанная сумма за прошлый месяц 52 536 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
РАЗДЕЛЫ САЙТА
Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
ЗАДАТЬ ВОПРОС
НОВЫЕ ОТВЕТЫ
- Абадзехская стоянка, Даховская пещера. ..
- По закону сохранения заряда каждый шарик после соприкасl..
- 2)прогудел первый мохнатый шмель 3) Зазвенела Прогудел 4) ..
- В мілкій траві ворушаться сліди веселих, сполоханих доще
..
ПОХОЖИЕ ВОПРОСЫ
- В тетраэдре DABC точка Е лежит на ребре AD. Постройте сечение тетраэдра, проходящее через точку Е параллельно прямым АС и DB. Определите вид пос…
- В тетраэдре SABC точка К лежит в плоскости ABC. Постройте сечение тетраэдра плоскостью MNK.
- В тетраэдре DABC все ребра равны а. Точки А1 В1 и С1 — середины ребер DA, DB и DC соответственно.
а) Постройте сечение тетраэдра, проходящее через т - В тетраэдре DABC точки М и К — середины ребер DA и ВС. Постройте сечение тетраэдра, проходящее через точки М и К параллельно прямой DC. Определит
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 — 2023 — UCHEES.RU
Избранные теоремы геометрии тетраэдра
Выпускная квалификационная
работа
Избранные теоремы геометрии
тетраэдра
Специальность / направление
подготовки Математика
Специализация / профиль Математика
— информатика
Содержание
Введение
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы о тетраэдрах
§1. Теорема Менелая
§2. Теорема Чевы
§3. Свойства медиан и бимедиан
тетраэдра
1.2 Различные виды тетраэдров.
§1. Пифагоровы тетраэдры
§2. Ортоцентрические тетраэдры
§3. Каркасные тетраэдры
§4. Равногранные тетраэдры
§5. Инцентрические тетраэдры
§6. Соразмерные тетраэдры
§7. Правильные тетраэдры
Глава II.
Тетраэдр в курсе математики средней
школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Введение
Интерес к изучению
тетраэдра возник у человечества с
древних времен и не угасает до сих пор.
Это связано не только с его красотой,
но и с большой практической ценностью.
Тетраэдр является
одним из основных фигур стереометрии,
однако его изучение в курсе средней
школы недостаточно подробно. В некоторых
учебниках авторы избегают самой
терминологии, предпочитая называть
фигуру «треугольной пирамидой» (и
рассматривают её именно в таком ключе),
а об изучении различных видов тетраэдров
зачастую и говорить не приходится.
Роль задач о тетраэдрах
в математическом развитии школьников
трудно переоценить. Они стимулируют
накопление конкретных геометрических
представлений, способствуют развитию
пространственного мышления, что особенно
важно в процессе изучения стереометрии.
Изучению тетраэдра как школе,
так и в вузах посвящено лишь небольшое
количество занятий, поэтому целью
дипломной работы является изучение
различных видов тетраэдров, а также
теорем, связанных с геометрией тетраэдра.
В соответствии с целью сформулированы
следующие задачи:
Собрать сведения о тетраэдре
из различных источников и привести их
в систему; разобрать доказательства
теорем, связанных с тетраэдром;
Проанализировать
методику изложения материала в различных
школьных учебниках;
Разработать курс занятий о
тетраэдре для средней школы.
В первой главе моей
дипломной работы речь пойдёт о различных
видах тетраэдра и некоторых теоремах,
касающихся этой фигуры. Вторая глава
посвящена анализу учебного материала
для средней школы по заданной теме и
разработке курса занятий.
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы
о тетраэдрах
§1. Теорема Менелая
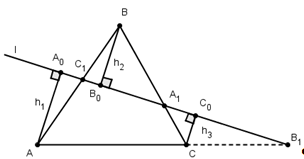
Теорема Менелая для треугольника.
Пусть точки А>1>>
>и С>1>
лежат на сторонах ВC
и АC
треугольника АВС,
точка В>1>>
>на продолжении стороны
АС этого
треугольника. Для того чтобы точки А>1>,
В>1>,
С>1>
лежали на одной прямой необходимо и
достаточно, чтобы выполнялось равенство
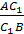
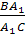
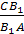
Доказательство.
Сначала докажем необходимость.
Пусть точки А>1>,В>1>,С>1>
лежат на прямой l
и AA>0>=h>1>,
CC>0>=h>3>>
>- перпендикуляры, опущенные
соответственно из точек А,
В, С на прямую l.
Из подобия треугольников АА>0>С>1>>
>и ВВ>0>С>1>>
>получаем
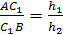
Аналогично, рассматривая другие пары
подобных треугольников, получаем
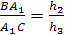
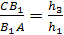
Перемножая полученные пропорции,
приходим к требуемому равенству.
Теперь докажем достаточность.
Пусть точки А>1>,
В>1>, С>1>,
лежащие на прямых ВС, АС, АВ таковы, что
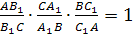
Докажем, что точки А>1>,
В>1>,
С>1>
лежат на одной прямой.
Проведем прямую А>1>В>1>>
>и докажем, что точка С>1>
ей принадлежит. Предположим, что это не
так. Сначала заметим, прямая А>1>В>1>>
>не параллельна прямой
АВ. Пусть Т
— точка пересечения А>1>В>1>>
>и АВ,
тогда
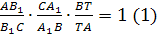
Из условия и равенства (1) следует, что
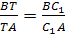
Так как точки Т
и С>1>>
>лежат вне отрезка АВ,
их совпадение вытекает из следующей
леммы.
Лемма 1.
Пусть А и В две различные точки,
тогда для любого k>0, k≠1 на прямой АВ
существуют две точки U и V такие, что
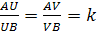
причем одна из этих точек принадлежит
отрезку АВ, а другая лежит вне отрезка.
Доказательство.
Введем на прямой АВ
координаты, приняв точку А
за начало координат. Пусть для
определенности k>1,
тогда координата искомой точки U,
лежащей внутри отрезка АВ,
удовлетворяет уравнению
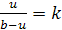
откуда
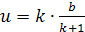
Точка V
находится вне отрезка AB,
из уравнения
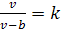
откуда
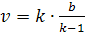
Случай 0<k<1
отличается от рассмотренного лишь тем,
что точку V
следует искать левее точки А.
Теорема Менелая допускает
интересное стереометрическое обобщение.
Теорема Менелая для тетраэдра.
Если плоскость μ
пересекает ребра АВ, ВС, CD
и DA тетраэдра
АВСD в точках
А>1>,
В>1>,
С>1>,
D>1>, то
(2).
Обратно, если для четырех точек
А>1>,
В>1>,
С>1>,
D>1>,
лежащих соответственно
на ребрах АВ, ВС, СD, DA
тетраэдра, выполнено равенство (2), то
эти четыре точки лежат в одной плоскости.
Доказательство.
Пусть h>1>,
h>2>,
h>3, >h>4>>
>- расстояния от точек
А, В, С, D соответственно до
плоскости μ,
тогда
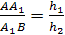
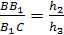
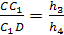
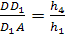
Осталось перемножить полученные
отношения.
Для доказательства обратной
теоремы построим плоскость А>1>,
В>1>, С>1>.
Пусть эта плоскость пересекает ребро
DA в точке Т.
По доказанному
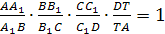
а по условию
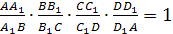
поэтому (и по лемме) точки Т
и D>1>>
>совпадают.>
>Утверждение доказано.
§2. Теорема Чевы
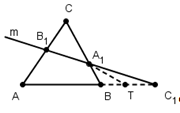
Теорема Чевы для треугольника.
Пусть точки А>1>,
В>1>,С>1>>
>лежат соответственно на
сторонах ВС, АС
и ВА треугольника
АВС (см. рис).
Для того чтобы отрезки АА>1>,
ВВ>1>,
СС>1>
пересекались в одной точке, необходимо
и достаточно, чтобы выполнялось
соотношение:
(3) (отрезки АА>1>,
ВВ>1>,
СС>1>>
>иногда называют чевианами).
Доказательство.
Необходимость. Пусть отрезки
АА>1>,
ВВ>1>,
СС>1>>
>пересекаются в точке М
внутри треугольника АВС.
Обозначим через S>1>,
S>2>,
S>3>>
>площади треугольников
АМС, СМВ, АМВ,
а через h>1>,
h>2> —
расстояния от точек А
и В до прямой
МС. Тогда
аналогично
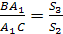
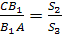
Перемножив полученные пропорции,
убеждаемся в справедливости теоремы.
Достаточность. Пусть точки А>1>,
В>1>,
С>1>>
>лежат на сторонах ВС,
СА, АС треугольника, и
выполнено соотношение (3), М
— точка пересечения отрезков АА>1>и
ВВ>1>,
а отрезок СМ
пересекает сторону АВ
в точке Q.
Тогда, по уже доказанному
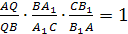
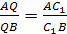
Из леммы снова следует совпадение точек
Q=C>1>.
Достаточность доказана.
Перейдем теперь к пространственному
обобщению теоремы Чевы.
Теорема Чевы для тетраэдра.
Пусть М
— точка внутри тетраэдра АВСD,
а А>1>,
В>1>,
С>1>
и D>1> —
точки пересечения плоскостей СМD,
AMD, АМВ и СМВ
с ребрами АВ, ВC,
СD и DA
соответственно. Тогда
(4). Обратно: если для точек
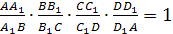
то плоскости АВС,
ВСD>1>
и DAB>1>>
>проходят через одну точку.
Доказательство.
Необходимость легко получить,
если заметить, что точки А>1>,
В>1>,>
>С>1>,
D>1>
лежат в одной плоскости (эта плоскость
проходит через прямые А>1>С>1>
и В>1>D>1>,
пересекающиеся в точке М),
и применить теорему Менелая. Обратная
теорема доказывается так же, так и
обратная теореме Менелая в пространстве:
нужно провести плоскость через точки
А>1>,
В>1>,
С>1> и
доказать с помощью леммы, что эта
плоскость пересечет ребро DA
в точке D>1>.
§3. Свойства медиан и бимедиан
тетраэдра
Медианой тетраэдра называется
отрезок, соединяющий вершину тетраэдра
с центром тяжести противоположной грани
(точкой пересечения медиан).
Теорема (Применение теоремы
Менелая).
Медианы тетраэдра пересекаются
в одной точке. Эта точка делит каждую
медиану в отношении 3:1, считая от вершины.
Доказательство.
Проведем две медианы: DD>1>
и CC>1>
тетраэдра ABCD.
Эти медианы пересекутся в точке F.
CL
– медиана грани ABC,
DL
– медиана грани ABD,
а D>1>,
C>1>
– центры тяжести грани ABC
и ABD.
По теореме Менелая:
и
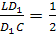
Запишем теорему для треугольника DLD>1>:
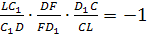
=>
Доказательство производится аналогично
для любой другой пары медиан.
Теорема (Применение теоремы
Чевы).
Для начала дадим определения
некоторых элементов тетраэдра. Отрезок,
соединяющий середины скрещивающихся
ребер тетраэдра называется бимедианой.
Бивысотами (по аналогии) называют общие
перпендикуляры скрещивающихся ребер.
Теорема.
Бимедианы тетраэдра пересекаются
в той же самой точке, что и медианы
тетраэдра.
Доказательство.
В треугольнике LDC
отрезки DC
и LF
пересекутся в точке K.
По теореме Чевы для этого треугольника:
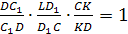
т.е.
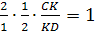
CK=KD,
LK
– бимедиана.
Замечание 1.
FL=FK.
Теорема Менелая для треугольника DLK:
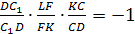
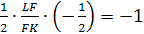
отсюда LF=FK.
Замечание 2.
Точка F
является центром тяжести тетраэдра.
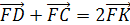
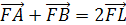
значит
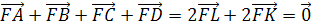
1.2 Различные
виды тетраэдров
§1. Пифагоровы
тетраэдры
Треугольник называется пифагоровым,
если у него один угол прямой, а отношение
любых сторон рационально (т.е применяя
подобие, можно из него получить
прямоугольный треугольник с целыми
длинами сторон).
По аналогии с этим, тетраэдр
называют пифагоровым, если его плоские
углы при одной из вершин прямые, а
отношение любых двух ребер рационально
(из него с помощью подобия можно получить
тетраэдр с прямыми плоскими углами при
одной из вершин и целыми длинами ребер).
Попробуем вывести «Уравнение
пифагоровых тетраэдров», т.е. такое
уравнение с тремя неизвестными ξ, η, ζ,
что любой пифагоров тетраэдр дает
рациональное решение этого уравнения,
и наоборот, любое рациональное решение
уравнения дает пифагоров тетраэдр.
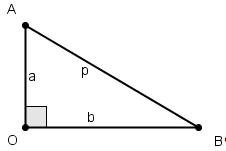
Сначала дадим способ описания
всех пифагоровых треугольников.
На рисунке треугольник ОАВ
— прямоугольный, длины его катетов
обозначены через а
и b, а дина
гипотенузы — через р.
Число
(1) условимся называть параметром
прямоугольного треугольника ОАВ
(или точнее, параметром «относительно
катета а«).
Используя соотношение р2=а2+b2,
имеем:
Из этих уравнений непосредственно
получим формулы, выражающие отношения
сторон прямоугольного треугольника
через его параметр:
и
(2).
Из формул (1) и (2) непосредственно
вытекает следующее утверждение: для
того, чтобы прямоугольный треугольник
был пифагоровым, необходимо и достаточно,
чтобы число ξ было рациональным. В самом
деле, если треугольник пифагоров, то из
(1) следует, что ξ рационально. Обратно,
если ξ рационально, то согласно (2)
отношения сторон рациональны, то есть
треугольник пифагоров.
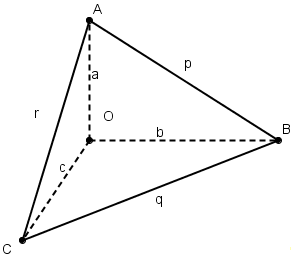
Пусть теперь ОАВС
— тетраэдр, у которого плоские углы при
вершине О
прямые. Длины ребер, исходящих из вершины
О, обозначим через a,b,с,
а длины оставшихся ребер через р,
q, r.
Рассмотрим параметры трех
прямоугольных треугольников ОАВ,
ОВС, ОСА:
(3)
Тогда по
формулам (2) можно выразить отношения
сторон этих прямоугольных треугольников
через их параметры:
(4),
(5).
Из (4) непосредственно
вытекает, что параметры ξ,
η, ζ, удовлетворяют
соотношению
(6). Это и есть общее уравнение пифагоровых
тетраэдров.
Из формул (3) — (5) непосредственно
вытекает следующее утверждение: для
того чтобы тетраэдр ОАВС
с прямыми плоскими углами при вершине
О был пифагоровым, необходимо и достаточно,
чтобы параметры ξ, η, ζ
(удовлетворяющие уравнению (6)) были
рациональными.
Продолжая аналогию пифагорова
треугольника с пифагоровым тетраэдром,
попробуем сформулировать и доказать
пространственное обобщение теоремы
Пифагора для прямоугольных тетраэдров,
которая, очевидно, будет верна и для
пифагоровых тетраэдров. В этом нам
поможет следующая лемма.
Лемма 1.
Если площадь многоугольника
равна S, то
площадь его проекции на плоскость π
равна
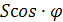
где φ — угол
между плоскостью π и плоскостью
многоугольника.
Доказательство.
Утверждение леммы очевидно для
треугольника, одна сторона которого
параллельна линии пересечения плоскости
π с плоскостью многоугольника. В самом
деле, длина этой стороны при проекции
не изменяется, а длина высоты, опущенной
на нее при проекции, изменяется в cosφ
раз.
Докажем теперь, что любой
многогранник можно разделить на
треугольники указанного вида.
Проведем для этого через все
вершины многоугольника прямые,
параллельные линии пересечения
плоскостей, многоугольник разрежется
при этом на треугольники и трапеции.
Остается разрезать каждую трапецию по
любой из ее диагоналей.
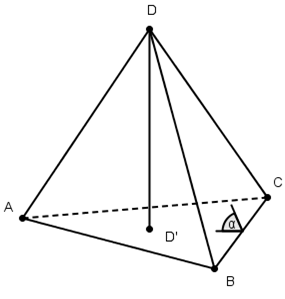
Теорема 1 (пространственная
теорема Пифагора).
В прямоугольном тетраэдре АВСD,
с плоскими углами при вершине D,
сумма квадратов площадей трех его
прямоугольных граней равна квадрату
площади грани АВС.
Доказательство.
Пусть α — угол между плоскостями
АВС и DВС,
D’ — проекция точки D
на плоскость АВС.
Тогда S>ΔDBC>=СоsαS>ΔАBC>>
>и S>ΔD’BC>=cоsαS>ΔDBC>>
>(по лемме 1), поэтому cоsα
=
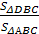
>S>Δ>>D>>‘>>BC>>
>=
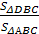
Аналогичные равенства можно
получить и для треугольников D’АВ
и D’АС. Складывая
их и учитывая, что сумма площадей
треугольников D’ВС,
D’АС и D’АВ
равна площади треугольника АВС,
получаем требуемое.
Задача.
Пусть все плоские углы при вершине
D
прямые; a,b,c
– длины ребер, выходящих из вершины D
на плоскость ABC.
Тогда
Доказательство.
По теореме Пифагора для
прямоугольного тетраэдра
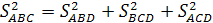
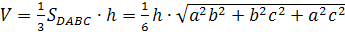
С другой
стороны
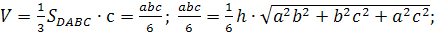
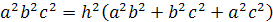
1=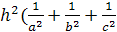
=>
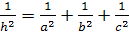
§2. Ортоцентрические
тетраэдры
В отличие от треугольника, высоты
которого всегда пересекаются в одной
точке — ортоцентре, не всякий тетраэдр
обладает аналогичным свойством. Тетраэдр,
высоты которого пересекаются в одной
точке, называется ортоцентрическим. мы
начнем изучение ортоцентрических
тетраэдров с необходимых и достаточных
условий ортоцентричности, каждое из
которых можно принять за определение
ортоцентрического тетраэдра.
(1) Высоты тетраэдра пересекаются
в одной точке.
(2) Основания высот тетраэдра
являются ортоцентрами граней.
(3) Каждые два противоположных
ребра тетраэдра перпендикулярны.
(4) Суммы квадратов противоположных
ребер тетраэдра равны.
(5) Отрезки, соединяющие середины
противоположных ребер тетраэдра, равны.
(6) Произведения косинусов
противоположных двугранных углов равны.
(7) Сумма квадратов площадей
граней вчетверо меньше суммы квадратов
произведений противоположных ребер.
Докажем некоторые из них.
Доказательство (3).
Пусть каждые два противоположных
ребра тетраэдра перпендикулярны.
Следовательно, высоты тетраэдра
попарно пересекаются. Если несколько
прямых попарно пересекаются, то они
лежат в одной плоскости или проходят
через одну точку. В одной плоскости
высоты тетраэдра лежать не могут, так
как иначе в одной плоскости лежали бы
и его вершины, поэтому они пересекаются
в одной точке.
Вообще говоря, для того чтобы
высоты тетраэдра пересекались в одной
точке, необходимо и достаточно потребовать
перпендикулярность только двух пар
противоположных ребер. Доказательство
этого предложения напрямую следует из
следующей задачи.
Задача 1.
Дан произвольный тетраэдр ABCD.
Докажите, что
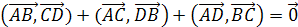
Решение.
Пусть а=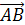
b=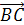
с=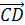
Тогда
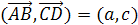
и
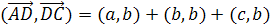
складывая эти равенства, получаем
требуемое.
Далее докажем свойство (4).
Пусть а=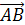
b=
и с=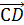
Равенство
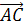
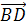
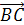
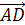
что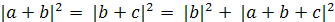
т.е. (а,с)=0.
Применяя данный алгоритм к другим парам
противоположных ребер, очевидно, получим
искомое утверждение.
Приведем оказательство свойства
(6).
Для доказательства используем
следующие теоремы:
Теорема
синусов. «Произведение длин двух
противоположных ребер тетраэдра,
деленное на произведение синусов
двугранных углов при этих ребрах, одно
и то же для всех трех пар противоположных
ребер тетраэдра».
Теорема
Бертшнейдера. «Если a
и b
– длины двух скрещивающихся ребер
тетраэдра, а
— двугранные углы при этих ребрах, то
величина
не зависит от выбора пары скрещивающихся
ребер.
Воспользовавшись теоремой
синусов для тетраэдра и теоремой
Бертшнейдера, получаем, что произведения
косинусов противоположных двугранных
углов равны тогда и только тогда, когда
равны суммы квадратов противоположных
ребер, из чего и следует справедливость
свойства (6) ортоцентрического тетраэдра.
В заключение пункта об
ортоцентрическом тетраэдре решим
несколько задач на эту тему.
Задача 2.
Докажите, что в ортоцентрическом
тетраэдре выполняется соотношение
ОН2=4R2-3d2,
где О — центр
описанной сферы, H
— точка пересечения высот, R
— радиус описанной сферы, d
— расстояние между серединами
противоположных ребер.
Решение.
Пусть К
и L — середины
ребер АВ и СD
соответственно. Точка Н
лежитт в плоскости, проходящей через
СD перепендикулярно
АВ, а точка О
— в плоскости, проходящей черех К
перпендикулярно АВ.
Эти плоскости симметричны
относительно центра масс тетраэдра —
середины отрезка KL.
Рассматривая такие плоскости для всех
ребер, получаем, что точки Н
и О симметричны
относительно М,
а значит КLМО
— параллелограмм. Квадраты его сторон
равны
и
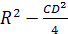
поэтому
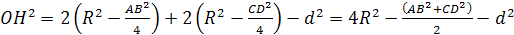
Рассматривая сечение, проходящее через
точку М
параллельно АВ
и СD, получаем
что АВ2+CD2=4d2.
Здесь можно добавить, что прямую,
на которой лежат точки О,
М и Н,
называют прямой Эйлера ортоцентрического
тетраэдра.
Замечание.
Наряду с прямой Эйлера можно
отметить существование сфер Эйлера для
ортоцентрического тераэдра, о которых
и пойдет речь в следующих задачах.
Задача 3.
Доказать, что для ортоцентрического
тетраэдра окружности 9 точек каждой
грани принадлежат одной сфере (сфере
24 точек). Для решения этой задачи
необходимо доказать условие следующей
задачи.
Задача 4.
Доказать, что середины сторон
треугольника, основания высот и середины
отрезков высот от вершин до точки их
пересечения лежат на одной окружности
— окружности 9 точек (Эйлер).
Доказательство.
Пусть АВС
— данный треугольник, Н
— точка пересечения его высот, А>1>,
В>1>,
С>1> —
середины отрезков АН, ВН,
СН; АА>2>
— высоты, А>3>
— середина ВС.
Будем считать для удобства, что АВС
— остроугольный треугольник. Поскольку


и ΔВ>1>А>2>С>1>=ΔВ>1>НС>1>,
то


—

т.е. точки А>1>,
В>1>,
А>2>,
С>1>>
>лежат на одной окружности.
Также легко увидеть, что


—

т.е. точки А>1>,
В>1>,
А>3>,
С>1>>
>тоже лежат на одной (а
значит на той же) окружности. Отсюда
следует, что все 9 точек, о которых
говорится в условии, лежат на одной
окружности. Случай тупоугольного
треугольника АВС
рассматривается аналогично.
Заметим, что окружность 9 точек
гомотетична описанной окружности с
центром в Н и коэффициентом
(именно так расположены треугольники
АВС и А>1>В>1>С>1>).
С другой стороны, окружность 9 точек
гомотетична описанной окружности с
центром в точке пересечения медиан
треугольника АВС
и коэффициентом
(именно так расположены треугольники
АВС и треугольник с вершинами в серединах
его сторон).
Теперь, после определения
окружности 9 точек, можно перейти к
доказательству условия задачи 3.
Доказательство.
Сечение ортоцентрического
тетраэдра любой плоскостью, параллельной
противоположным ребрам и проходящей
на равном расстоянии от этих ребер, есть
прямоугольник, диагонали которого равны
расстоянию между серединами противоположных
ребер тетраэдра ( все эти расстояния
равны между собой, см. необходимое и
достаточное условие ортоцентричности
(5). Отсюда следует, что середины всех
ребер ортоцентрического тетраэдра
лежат на поверхности сферы, центр которой
совпадает с центром тяжести данного
тетраэдра, а диаметр равен расстоянию
между серединами противоположных ребер
тетраэдра. Значит, все четыре окружности
9 точек лежат на поверхности этой сферы.
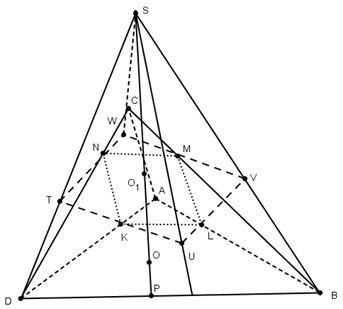
Задача 5.
Доказать, что для ортоцентрического
тетраэдра центры тяжести и точки
пересечения высот граней, а также точки
, делящие отрезки каждой высоты тетраэдра
от вершины до точки пересечения высот
в отношении 2:1, лежат на одной сфере (
сфере 12 точек).
Доказательство.
Пусть точки О, М
и Н — соответственно
центр описанного шара, ценетр тяжести
и ортоцентр ортоцентрического тетраэдра;
М — середина
отрезка ОН
(см. задачу 2). Центры тяжести граней
тетраэдра служат вершинами тетраэдра,
гомотетичного, с центром гомотетиии в
точке М и
коэффициентом
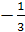
при этой гомотетии точка О
перейдет в точку О>1>,
расположенную на отрезке МН
так, что
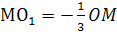
О>1>
будет центром сферы проходящей через
центры тяжестей граней.
С другой стороны, точки, делящие
отрезки высот тетраэдра от вершин до
ортоцентра в отношении 2:1, служат
вершинами тетраэдра, гомотетичного
данному с центром гомотетии в Н
и коэффициентом
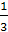
При этой гомотетии точка О,
как легко видеть, перейдет в ту же точку
О>1>.
Таким образом, восемь из двенадцати
точек лежат на поверхности сферы с
центром в О>1>
и радиусом, втрое меньшим, чем радиус
сферы, описанной около тетраэдра.
Докажем, что точки пересечения
высот каждой грани лежат на поверхности
той же сферы.
Пусть О`, Н`
и М` — центр
описанной окружности, точка пересечения
высот и центр тяжести какой-либо грани.
О` и Н`
являются проекциями точек О
и Н на плоскость
этой грани, а отрезок М`
делит отрезок О`Н`
в отношении 1:2, считая от О`(известный
планиметрический факт). Теперь легко
убедиться (см. рис), что проекция О>1>
на плоскость этой грани — точка О`>1>
совпадает с серединой отрезка М`Н`,
т.е. О>1>>
>равноудалена от М`
и Н`, что и
требовалось.
§3. Каркасные
тетраэдры
Каркасным называется тетраэдр,
для которого существует сфера, касающаяся
всех шести ребер тетраэдра. Не всякий
тетраэдр каркасный. Например, легко
понять, что нельзя построить сферу,
касающуюся всех ребер равногранного
тетраэдра, если его описанный параллелепипед
«длинный».
Перечислим свойства каркасного
тетраэдра.
(1) Существует сфера, касающаяся
всех ребер тетраэдра.
(2) Суммы длин скрещивающихся
ребер равны.
(3) Суммы двугранных углов при
противоположных ребрах равны.
(4) Окружности, вписанные в грани,
попарно касаются.
(5) Все четырехугольники,
получающиеся на развертке тетраэдра,
— описанные.
(6) Перпендикуляры, восстановленные
к граням из центров вписанных в них
окружностей, пересекаются в одной точке.
Докажем несколько свойств
каркасного тераэдра.
Доказательство (2).
Пусть О
— центр сферы, касающейся четырех ребер
во внутренних точках. заметим теперь,
что если из точки Х
провести касательные ХР
и ХQ к сфере с
центром О, то
точки Р и Q
симметричны относительно плоскости,
проходящей прямую ХО
и середину отрезка PQ,
а значит плоскости РОХ
и QОХ образуют
с плоскостью ХРQ
равные углы.
Проведем 4 плоскости, проходящие
через точку О и рассматриваемые ребра
тетраэдра. Они разбивают каждый из
рассматриваемых двугранных углов на
два двугранных угла. Выше было показано,
что полученные двугранные углы,
прилегающие к одной грани тетраэдра,
равны. Как в одну, так и в другую
рассматриваемую сумму двугранных углов
входит по одному полученному углу для
каждой грани тетраэдра. Проводя
аналогичные рассуждения для других пар
скрещивающихся ребер, получим
справедливость свойства (2).
Вспомним некоторые свойства
описанного четырехугольника:
Плоский
четырехугольник будет описанным тогда
и только тогда, когда суммы его
противоположных сторон равны;
Если
описанный четырехугольник разбить
диагональю на два треугольника, то
вписанные в треугольники окружности
касаются
Учитывая эти свойства, легко
доказать остальные свойства каркасного
тетраэдра. Свойство (3) тетраэдра напрямую
следует из свойства (b), а свойство (4) из
свойства (a)
и свойства (1) тетраэдра. Свойство (5) из
свойства (3). Действительно, ведь окружности
вписанные в грани тетраэдра, являются
пересечениями его граней со сферой,
касающейся ребер, откуда очевидно, что
перпендикуляры, восстановленные в
центрах вписанных в грани окружностей
неминуемо пересекутся в центре этой
сферы.
Задача 1.
Сфера касается ребер АВ,
ВС, СD и DA
тетраэдра АВСD
в точках L, M, N, K,
являющихся вершинами квадрата. Докажите,
что если эта сфера касается ребра АС,
то она касается и ребра BD.
Решение.
По условия КLMN
— квадрат. Проведем через точки К,
L, M, N плоскости, касающиеся
сферы. Т.к все эти плоскости одинаково
наклонены к плоскости КLMN,
то они пересекаются в одной точке S,
расположенной на прямой ОО>1>,
где — центр сферы, а О>1>>
>- центр квадрата. Эти
плоскости пересекают поверхность
квадрата KLMN
по квадрату TUVW,
серединами сторон которого являются
точки К, L, M, N.
В четырехгранном угле STUVW с вершиной S
все плоские углы равны, а точки К,
L, M, N лежат на биссектрисах
его плоских углов, причем SK=SL=SM=SN.
Следовательно,
SA=SC и SD=SB,
а значит АК=АL=CM=CN
и ВL=BM=DN=DK. По
условию АС
тоже касается шара, поэтому АC=АК+CN=2АК.
А так как SK —
биссектриса угла DSA,
то DK:КА=DS:SA=DВ:АС.
Из равенства АС=2АК
следует теперь, что DВ=2DK.
Пусть Р —
середина отрезка DВ,
тогда Р лежит
на прямой SO.
Треугольники DOK
и DOP равны,
т.к. DK=DP и


Поэтому ОР=ОК=R,
где R — радиус
сферы, а значит, DB
тоже касается сферы.
§4. Равногранные
тетраэдры
Равногранным называется тетраэдр,
все грани которого равны. Чтобы представить
себе равногранный тетраэдр, возьмем
произвольный остроугольный треугольник
из бумаги, и будем сгибать его по средним
линиям. Тогда три вершины сойдутся в
одну точку, а половинки сторон сомкнутся,
образуя боковые ребра тетраэдра.
(0) Грани конгруэнтны.
(1) Скрещивающиеся ребра попарно
равны.
(2) Трехгранные углы равны.
(3) Противолежащие двугранные
углы равны.
(4) Два плоских угла, опирающихся
на одно ребро, равны.
(5) Сумма плоских углов при каждой
вершине равна 180°.
(6) Развертка тетраэдра — треугольник
или параллелограмм.
(7) Описанный параллелепипед
прямоугольный.
(8) Тетраэдр имеет три оси симметрии.
(9) Общие перпендикуляры
скрещивающихся ребер попарно
перпендикулярны.
(10) Средние линии попарно
перпендикулярны.
(11) Периметры граней равны.
(12) Площади граней равны.
(13) Высоты тетраэдра равны.
(14) Отрезки, соединяющие вершины
с центрами тяжести противоположных
граней, равны.
(15) Радиусы описанных около граней
окружностей равны.
(16) Центр тяжести тетраэдра
совпадает с центром описанной сферы.
(17) Центр тяжести совпадает с
центром вписанной сферы.
(18) Центр описанной сферы совпадает
с центром вписанной.
(19) Вписанная сфера касается
граней в центрах описанных около этих
граней окружностей.
(20) Сумма внешних единичных
нормалей (единичных векторов,
перпендикулярных к граням), равна
нулю.
(21) Сумма всех двугранных углов
равна нулю.
Практически все свойства
равногранного тетраэдра следуют из его
определения, поэтому докажем
только некоторые из них.
Доказательство (16).
Т.к. тетраэдр ABCD
равногранный, то по свойству (1) AB=CD.
Пусть точка К
отрезка АВ, а
точка L середина
отрезка DC,
отсюда отрезок KL
бимедиана тетраэдра ABCD,
откуда по свойствам медиан тетраэдра
следует, что точка О
— середина отрезка KL,
является центром тяжести тетраэдра
ABCD.
К тому же медианы тетраэдра
пересекаются в центре тяжести, точке
О, и делятся
этой точкой в отношении 3:1, считая от
вершины. Далее, учитывая вышесказанное
и свойство (14) равногранного тетраэдра,
получаем следующее равенство отрезков
АО=ВО=СО=DО, из
которого и следует, что точка О
является центром описанной сферы (по
определению описанной около многогранника
сферы).
Обратно. Пусть К
и L — середины
ребер АВ и СD
соответственно, точка О
— центр описанной сферы тетраэдра, т.е.
середина отрезка KL.
Т.к. О — центр
описанной сферы тетраэдра, то треугольники
AOB и COD
— равнобедренные с равными боковыми
сторонами и равными медианами OK
и OL. Поэтому
ΔAOB=ΔCOD.
А значит AB=CD.
Аналогично доказывается равенство
других пар противоположных ребер, из
чего по свойству (1) равногранного
тетраэдра и будет следовать искомое.
Доказательство (17).
Рассмотрим биссектор двугранного
угла при ребре AB,
он разделит отрезок DC в отношении
площадей граней ABD
и ABC.
Т.к. тетраэдр ABCD
равногранный, то по свойству (12)
S>ΔABD>=S>ΔABD>=>DL=LС,
откуда следует, что биссектор ABL
содержит бимедиану KL.
Применяя аналогичные рассуждения для
остальных двугранных углов, и принимая
во внимание тот факт, что биссекторы
тетраэдра пересекаются в одной точке,
которая является центром вписанной
сферы, получаем, что эта точка неминуемо
будет центром тяжести данного равногранного
тетраэдра.
Обратно. Из того, что центр тяжести
и центр вписанной сферы совпадают имеем
следующее: DL=LC=>SABD=SADC.
Доказывая подобным образом равновеликость
всех граней и, применяя свойство (12)
равногранного тетраэдра, получаем
искомое.
Теперь докажем свойство (20). Для
этого сначала нужно доказать одно из
свойств произвольного тетраэдра.
тетраэдр теорема
школьный учебник
Лемма 1.
Если длины векторов перпендикулярных
к граням тетраэдра численно равны
площадям соответствующих граней, то
сумма этих векторов равна нулю.
Доказательство.
Пусть Х
— точка внутр и многогранника, h>i
>(i=1,2,3,4)
— расстояние от нее до плоскости i-ой
грани.
Разрежем многогранник на пирамиды
с вершиной Х,
основаниями которых служат его грани.
Объем тетраэдра V
равен сумме объемов этих пирамид, т.е.
3 V=∑h>i>S>i>,
где S>i>>
>площадь i-ой
грани. Пусть далее, n>i>>
>- единичный вектор внешней
нормали к i-ой грани, M>i >-
произвольная точка этой грани. Тогда
h>i >=(ХM>i>,
S>i>n>i>),
поэтому 3V=∑h>i>S>i>=∑(ХM>i>,
S>i>n>i>)=(ХО,
S>i>n>i>)+(ОM>i>,
S>i>n>i>)=(ХО,
∑S>i>n>i>)+3V,
где О — некоторая
фиксированная точка тетраэдра,
следовательно, ∑S>i>n>i>=0.
Далее очевидно, что свойство
(20) равногранного тетраэдра является
частным случаем вышеуказанной леммы,
где S>1>=>
>S>2>=>
>S>3>=>
>S>4>=>n>1>=n>2>=n>3>=n>4>,
и так как площади граней не равны нулю,
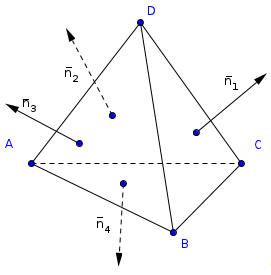
получаем верное равенство n>1>+n>2>+n>3>+n>4>=0.
В заключение рассказа о равногранном
тетраэдре приведем несколько задач на
эту тему.
Задача 1.
Прямая, проходящая через центр
масс тетраэдра и центр описанной около
него сферы, пересекает ребра AB
и CD. Докажите,
что AC=BD и AD=BC.
Решение.
Центр масс тетраэдра лежит на
прямой, соединяющей середины ребер АВ
и СD.
Следовательно, на этой прямой
лежит центр описанной сферы тетраэдра,
а значит, указанная прямая перпендикулярна
ребрам АВ и
СD. Пусть С`
и D` — проекции
точек C и D
на плоскость, проходящую через прямую
АВ параллельно
СD. Т.к. AC`BD`
— параллелограмм (по построению), то
АС=ВD и АD=ВС.
Задача 2.
Пусть h
— высота равногранного тетраэдра, h>1>>
>и h>2>>
>- отрезки, на которые одна
из высот грани делится точкой пересечения
высот этой грани. Доказать, что h2=4h>1>h>2>;
доказать также, что основание высоты
тетраэдра и точка пересечения высот
грани, на которую эта высота опущена,
симметричны относительно центра
окружности, описанной около этой грани.
Доказательство.
Пусть АВСD
— данный тетраэдр, DH
— его высота, DA>1>,
DВ>1>,
DС>1>>
>- высоты граней, опущенные
из вершины D
на стороны ВС, СА и АВ.
Разрежем поверхность тетраэдра
вдоль ребер DA, DB, DC,
и сделаем развертку. Очевидно, что Н
есть точка пересечения высот треугольника
D>1>D>2>D>3>.
Пусть F — точка
пересечения высот треугольника ABC,
АК — высота этого треугольника,
АF=h>1>,
FК=h>2>.
Тогда D>1>Н=2h>1>,
D>1>A>1>=h>1>-h>2>.
Значит, поскольку h
— высота нашего тетраэдра, h2=DН2=DA2
— НA>1>2=
(h>1+>
h>2>)2
— (h>1>—
h>2>)2=4h>1>h>2.>>
>Пусть теперь М
— центр тяжести треугольника ABC
(он же центр тяжести треугольника
D>1>D>2>D>3>),
О — центр
описанной около него окружности.
Известно, что F, М
и О лежат на
одной прямой (прямая Эйлера), причем М
— между F и О,
FM=2МО,
С другой стороны, треугольник D>1>D>2>D>3>>
>гомотетичен треугольнику
АВС с центром
в М и коэффициентом
(-2), значит МН=2FM.
Из этого следует, что ОН=FO.
Задача 3.
Доказать, что в равногранном
тетраэдре основания высот, середины
высот и точки пересечения высот граней
лежат на поверхности одной сферы (сферы
12 точек).
Доказательство.
Решая задачу 2, мы доказали, что
центр описанной около тетраэдра сферы
проецируется на каждую грань в середину
отрезка, концами которого является
основание высоты, опущенной на эту
грань, и точка пересечения высот этой
грани. А поскольку расстояние от центра
описанной около тетраэдра сферы до
грани равно
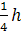
где h — высота
тетраэдра, центр описанной сферы удален
от данных точек на расстояние
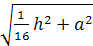
где а — расстояние
между точкой пересечения высот и центром
описанной около грани окружности.
§5. Инцентрические
тетраэдры
Отрезки, соединяющие центры
тяжести граней тетраэдра с противоположными
вершинами (медианы тетраэдра), всегда
пересекаются в одной точке, эта точка
— центр тяжести тетраэдра. Если в этом
условии заменить центры тяжести граней
на ортоцентры граней, то оно превратится
в новое определение ортоцентрического
тетраэдра. Если же заменить их на центры
вписанных в грани окружностей, называемых
иногда инцентрами, мы получим определение
нового класса тетраэдров — инцентрических.
Признаки класса инцентрических
тетраэдров тоже довольно интересны.
Отрезки,
соединяющие вершины тетраэдра с центрами
окружностей, вписанных в противоположные
грани, пересекаются в одной точке.
Биссектрисы
углов двух граней, проведенному к общему
ребру этих граней, имеют общее основание.
Произведения
длин противоположных ребер равны.
Треугольник,
образованный вторыми точками пересечения
трех ребер, выходящих из одной вершины,
с любой сферой, проходящей через три
конца этих ребер, является равносторонним.
Доказательство (2).
По свойству (1), если DF,
BE, CF, AM — биссектрисы
соответственных углов в треугольниках
АВС и FBD,
то отрезки КС
и LD будут иметь
общую точку I
(см. рис). Если же прямые DK
и СL не
пересекаются в точке F,
то, очевидно, КС
и DL не
пересекаются, чего быть не может (по
определению инцентрического тетраэдра).
Доказательство (3).
Учитывая свойство (2) и свойство
биссектрисы, получаем соотношения:
;
.
§6.
Соразмерные
тетраэдры
Соразмерными называются тетраэдры,
у которых
Бивысоты
равны.
Проекция
тетраэдра на плоскость, перпендикулярную
любой бимедиане, есть ромб.
Грани
описанного параллелепипеда равновелики.
4а2а>1>2—
(b2+b>1>2-c2-c>1>2)2=4b2b>1>2—
(c2+c>1>2-a2-a>1>2)2=4c2c>1>2—
(a2+a>1>2-b2-b>1>2)2,
где а
и а>1>,
b
и b>1>,
с
и с>1>
— длины противоположных ребер.
Для доказательства эквивалентности
определений (1) — (4) достаточно заметить,
что бивысоты тетраэдра равны высотам
параллелограмма, являющегося его
проекцией, упоминавшейся в свойстве
(2), и высотам описанного параллелепипеда,
и что квадрат площади параллелепипеда,
содержащей, скажем, ребро с,
равен
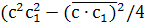
а скалярное произведение
выражается через ребра тетраэдра по
формуле (4).
Добавим сюда ещё два условия
соразмерности:
Для
каждой пары противоположных ребер
тетраэдра плоскости, проведенные через
одно из них и середину второго,
перпендикулярны.
В
описанный параллелепипед соразмерного
тетраэдра можно вписать сферу.
§7. Правильные тетраэдры
Если ребра тетраэдра равны между
собой, то равны между собой будут и
трехгранные, и двугранные, и плоские
углы. В таком случае тетраэдр называется
правильным. Заметим
также, что такой тетраэдр является и
ортоцентрическим, и каркасным, и
равногранным, и инцентрическим, и
соразмерным.
Замечание 1.
Если тетраэдр является равногранным
и принадлежит к одному из следующих
видов тетраэдров: ортоцентрический,
каркасный, инцентрический, соразмерный,
то он будет и правильным.
Замечание 2.
Тетраэдр является правильным,
если он принадлежит к двум любым видам
тетраэдров из перечисленных:
ортоцентрический, каркасный, инцентрический,
соразмерный, равногранный.
Свойства правильного тетраэдра:
Каждая его вершина является
вершиной трех треугольников. А значит,
сумма плоских углов при каждой вершине
будет равна 180º
В правильный тетраэдр можно
вписать октаэдр, притом четыре (из
восьми) грани октаэдра будут совмещены
с четырьмя гранями тетраэдра, все шесть
вершин октаэдра будут совмещены с
центрами шести рёбер тетраэдра.
Правильный тетраэдр состоит из
одного вписанного октаэдра (в центре)
и четырёх тетраэдров (по вершинам),
причем ребра этих тетраэдров и октаэдра
вдвое меньше ребер правильного тетраэдра
Правильный тетраэдр можно
вписать в куб двумя способами, притом
четыре вершины тетраэдра будут совмещены
с четырьмя вершинами куба.
Правильный тетраэдр можно
вписать в икосаэдр, притом, четыре
вершины тетраэдра будут совмещены с
четырьмя вершинами икосаэдра.
Задача 1.
Доказать, что скрещивающиеся
ребра правильного тетраэдра взаимно
перпендикулярны.
Решение:
Пусть DH – высота
правильного тетраэдра, точка H – центр
правильного ΔABC.
Тогда проекцией отрезка AD на плоскость
основания ABC будет отрезок BH.
Т.к. BHAC,
то по теореме о трех
перпендикулярах наклонная BD
AC.
Задача 2.
Дан правильный тетраэдр МАВС
с ребром 1. найдите расстояние между
прямыми AL и
МО, где
L-середина
ребра МС,
О-центр грани
АВС.
Решение:
1. Расстояние между двумя
скрещивающимися прямыми — это длина
перпендикуляра, опущенного из одной
прямой, к плоскости, параллельной этой
прямой и содержащей вторую прямую.
2. Строим проекцию AK
отрезка AL на
плоскость ABC.
Плоскость AKL
перпендикулярна плоскости ABC,
параллельна прямой MO
и содержит прямую AL.
Значит, искомая длина — это длина
перпендикуляра ON,
опущенного из точки O
к AK.
3. Найдем S>Δ>>KHA>
двумя способами.
S>Δ>=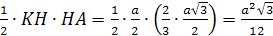
С другой стороны: S>Δ>>KHA>=
поэтому ρ
.
Найдём ON:
ρ
.
Задача 3.
Каждое ребро треугольной
пирамиды PABC равно
1; BD –
высота треугольника ABC .
Равносторонний треугольник BDE лежит
в плоскости, образующей угол ϕ с
ребром AC ,
причём точки P и E лежат
по одну сторону от плоскости ABC .
Найдите расстояние между точками P и E .
Решение. Поскольку
все рёбра пирамиды PABC равны,
это правильный тетраэдр. Пусть M
– центр
основания ABC , N
–
ортогональная проекция вершины E равностороннего
треугольника BDE на
плоскость ABC ,
K
–
середина BD ,
F
– основание
перпендикуляра, опущенного из точки E на
высоту PM тетраэдра
PABC .
Так как
EK 
то по теореме о трёх перпендикулярах
NK 
поэтому EKN –
линейный угол двугранного угла,
образованного плоскостями ABC и BDE ,
а т.к. NK
|| AC ,
то 
= ϕ .
Далее имеем:
BD
=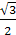
MD
= 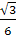
KD
= 
BD
= 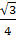
PM
= 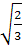
KM
= KD
— MD
= 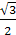
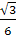
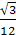
EK
= BD· 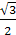

EN
= EK
sin
ϕ
= 
ϕ,
NK = EK cos
ϕ
= 
ϕ,
MN2 =
NK2 +
KM2 = 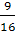
+ 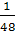
PE2 =
EF2 +
PF2 =
MN2 + (PM
— MF)2 =
MN2 + (PM
— EN)2 =
= 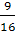
+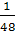
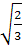

ϕ)2 = 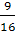
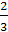
+ 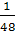
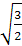
ϕ
+ 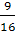
== 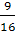
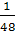

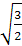
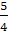
ϕ
= 
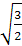
ϕ
= 
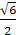
ϕ.
Следовательно,
PE =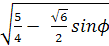
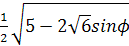
Задача 4.
Найди углы между скрещивающимися
высотами соседних граней тетраэдра.
Решение.
Случай №1.
Пусть BK
и DF – высоты
граней ABC и
BCD.

FD = α.
Обозначим длину ребра тетраэдра как a.
Проведем FL || BK,
тогда α
=
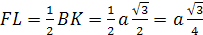
KL=LC.
Запишем теорему косинусов для
ΔDLF:
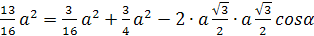
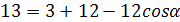
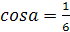
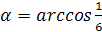
Случай
№2 (высота расположена иначе).
BK
и CN
– высоты граней ABC
и BCD. Проведем
FP || CN и FL
|| BK.
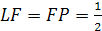
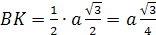
Найдем LP.
DO – высота правильного
тетраэдра, DO
=
, Q
– проекция P
на плоскость ABC,
.
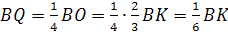
;
.
Запишем теорему косинусов для
ΔLFP:
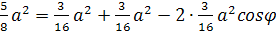
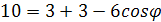
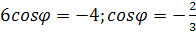
Так как угол между прямыми по
определению острый
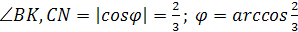
Глава II. Тетраэдр в курсе
математики средней школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
В школьном курсе
геометрии на изучение основ темы
«Тетраэдр» отводится достаточно много
времени. Методических проблем проведения
этой темы практически не возникает, так
как учащиеся знают, что такое пирамида
(в т.ч. и треугольная), как из пропедевтических
курсов прежних лет обучения математики,
так из жизненного опыта. Правильный
тетраэдр ассоциируется с его плоским
аналогом — правильным треугольником, а
равенство сторон с равенством ребер
или граней.
Однако проблемы в
изучении темы для учащихся существуют,
и разные учебники пытаются решить их
разными способами (порядком изложения
теоретического материала, уровнем
сложности задач и т.п.). Дадим краткую
характеристику распространенных
учебников геометрии в аспекте изучения
тетраэдра.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Атанасяна Л. С. и др.
В базовом
учебнике «Геометрия» для 10-11 классов
средней школы Атанасяна
Л. С. и др.
информацию о тетраэдре можно найти в 7
параграфах (12, 14, 28, 29, 32, 33, 69).
Авторы учебника
определяют тетраэдр как поверхность,
составленную из четырёх треугольников.
Из теоретической базы учебника для 10
класса можно почерпнуть знания о гранях,
рёбрах и вершинах тетраэдра, о построении
сечений тетраэдра плоскостью, вычислении
площади полной поверхности тетраэдра,
в т.ч. и усечённого (глава III, §
2 «Пирамида»).
Далее рассматриваются
правильные многогранники и элементы
симметрии правильных многогранников.
Формула нахождения объёма пирамиды
приводится в заключительной главе
учебника (глава VII «Объемы тел»).
Теоретический
материал учебника изложен компактно и
стилистически единообразно. Некоторый
теоретический материал расположен в
практической части учебника (доказательства
некоторых теорем производится в задачах).
Практический материал учебника разделён
на два уровня сложности (есть т.н. «задачи
повышенной трудности», отмеченные
специальным символом «*»). Кроме того,
в конце учебника есть задачник с задачами
высокой сложности, некоторые из которых
касаются тетраэдра. Рассмотрим некоторые
задачи учебника.
Решение задач.
Задача 1 (№300).
В правильной треугольной пирамиде DABC
точки E, F
и P
— середины сторон BC,
AB
и AD.
Определите вид сечения и найдите его
площадь, если сторона основания пирамиды
равна a,
боковое ребро равно b.
Решение.
Строим сечение
плоскостью, проходящей через точки E,
F, P. Проведём
среднюю линию треугольника ABC,
EF ||
AC,
EF ||
AC, а
AC
лежит в пл.
DCA,
значит EF
|| пл.
DCA. Плоскость
сечения пересечёт грань DCA
по прямой
PK.
Т.к. плоскость сечения
проходит через прямую EF
параллельную
плоскости DCA
и пересекает
плоскость DCA,
то линия
пересечения PK
параллельна
прямой EF.
Построим в грани BDA
отрезок
FP, а
в грани BDC
— отрезок
EK.
Четырёхугольник
EFOK и
есть искомое сечение. EF
|| AC,
PK || EF
|| AC,
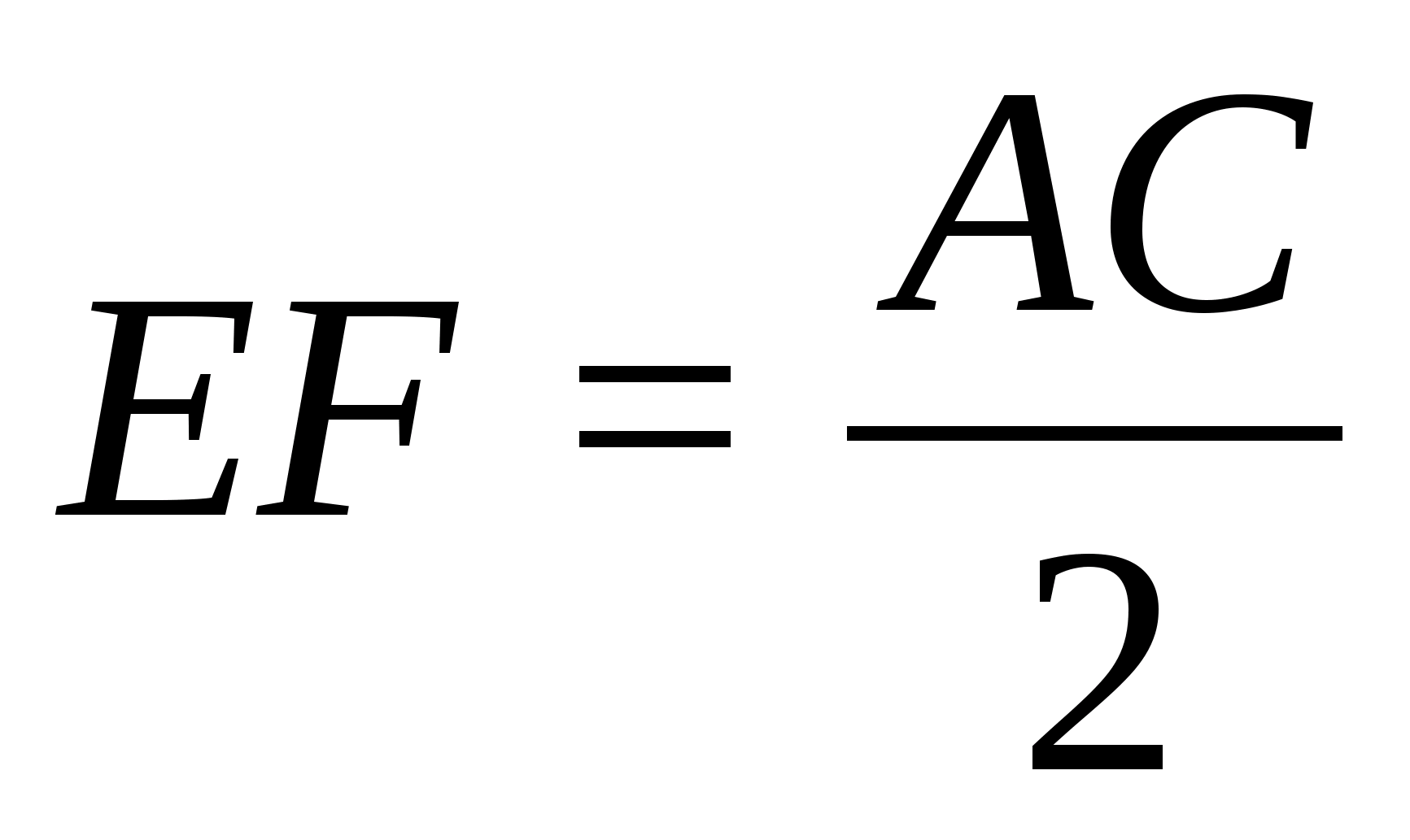
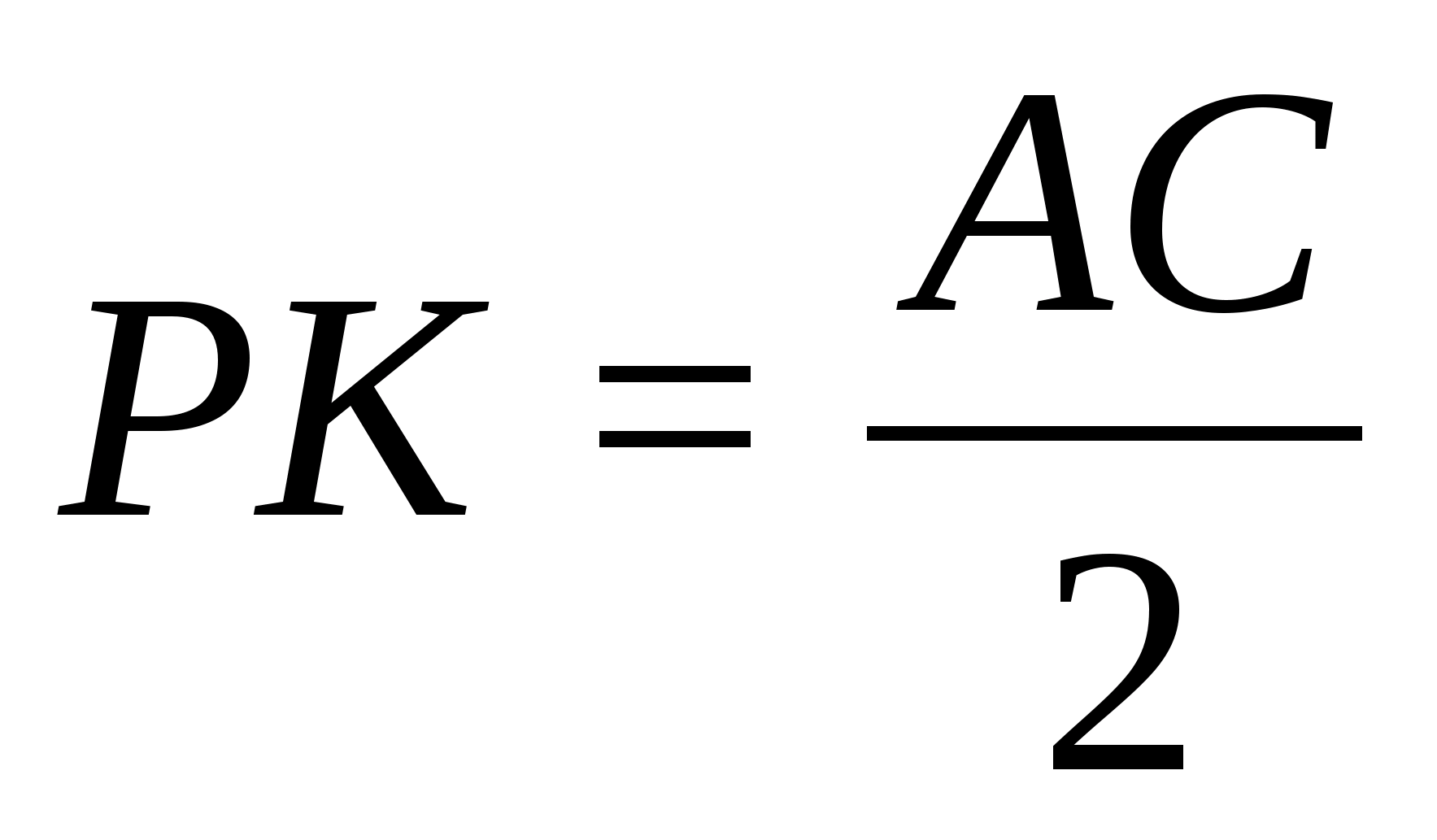
значит
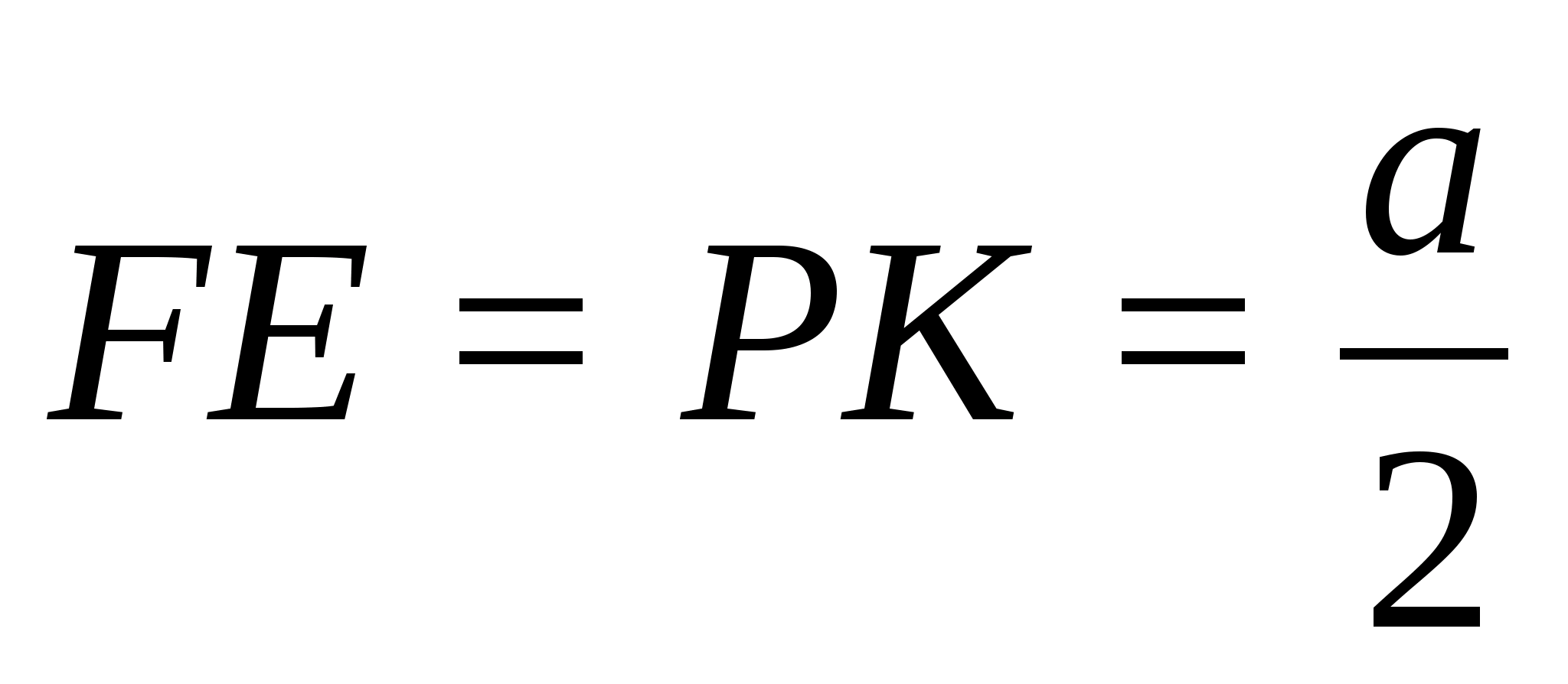
Т.к. PK
|| EF
и PK = EF,
то EFPK
— параллелограмм.
Таким образом, EK
|| EP, EP — средняя
линия треугольника BCD,
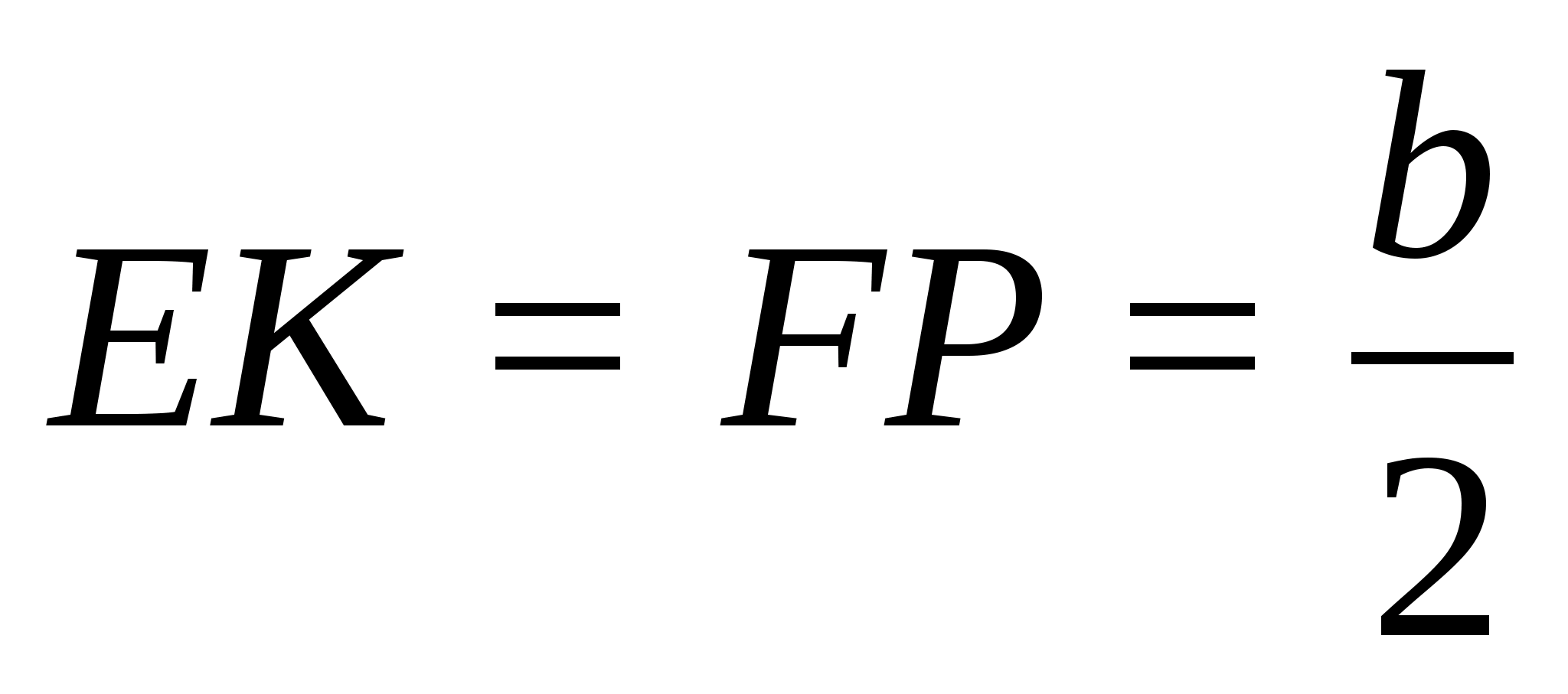
Угол между
скрещивающимися прямыми DB
и CA
равен 90°.
Докажем это. Построим высоту пирамиды
DO.
Точка O
— центр правильного треугольника ABC.
Продолжим отрезок BO
до пересечения со стороной AC
в точке M.
В правильном треугольнике ABC:
BM — высота,
медиана и биссектриса, следовательно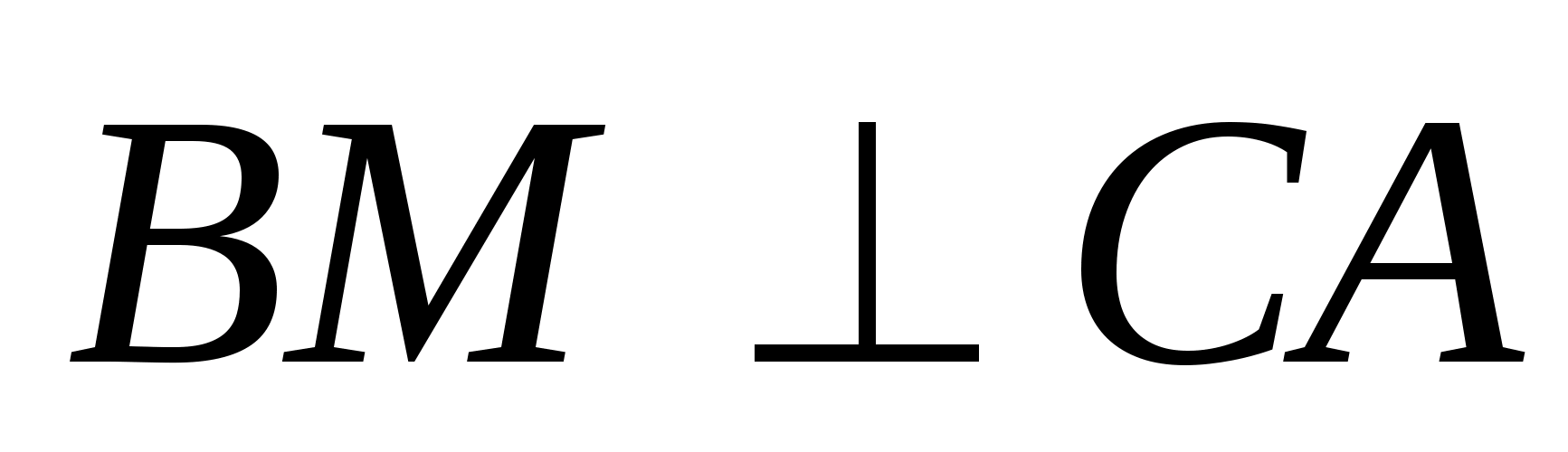
Имеем, что
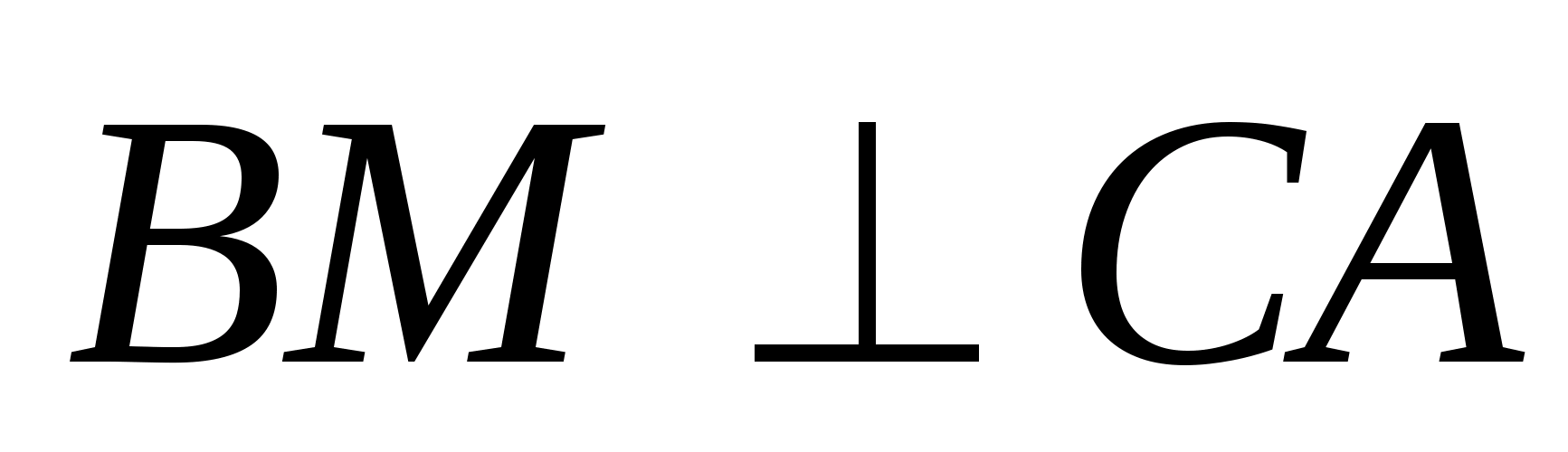
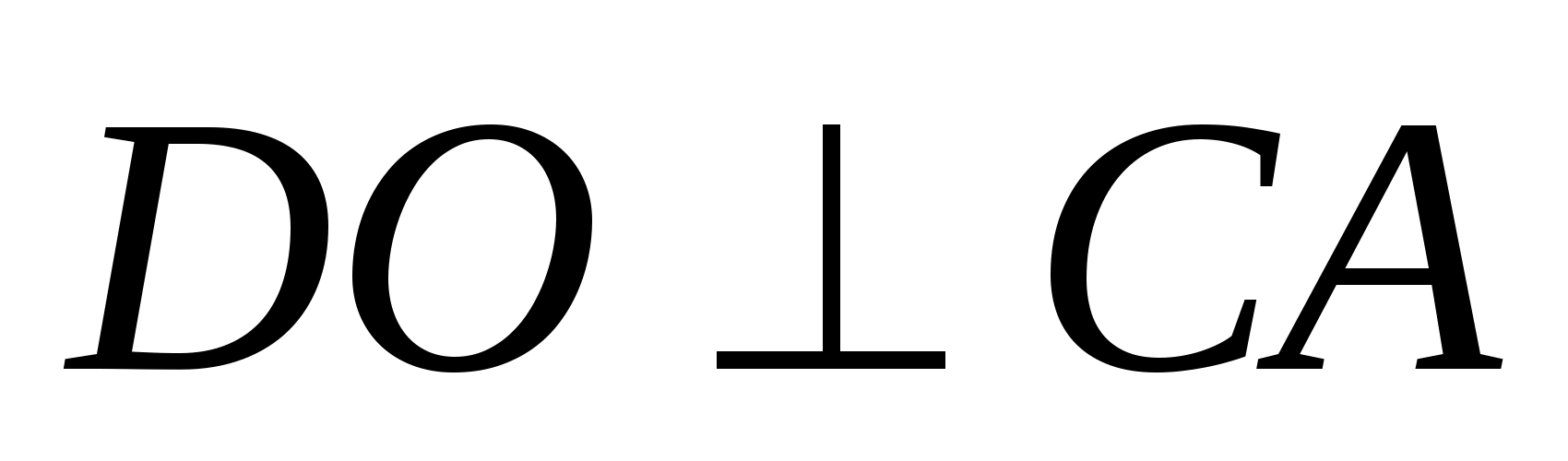
тогда по признаку перпендикулярности
прямой и плоскости
тогда
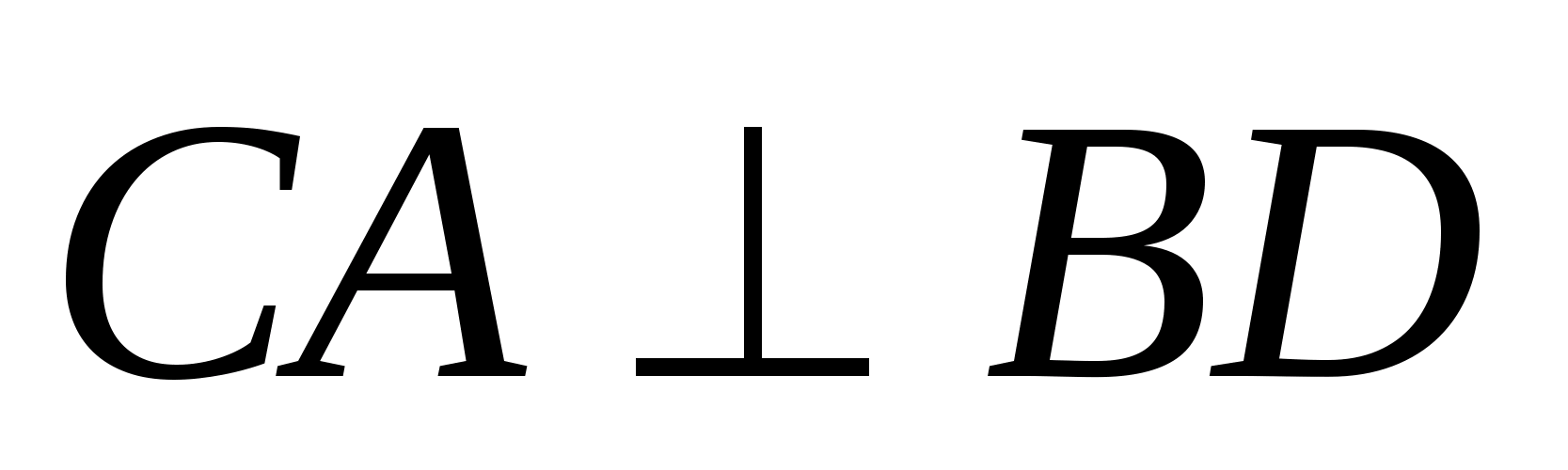
Т.к.
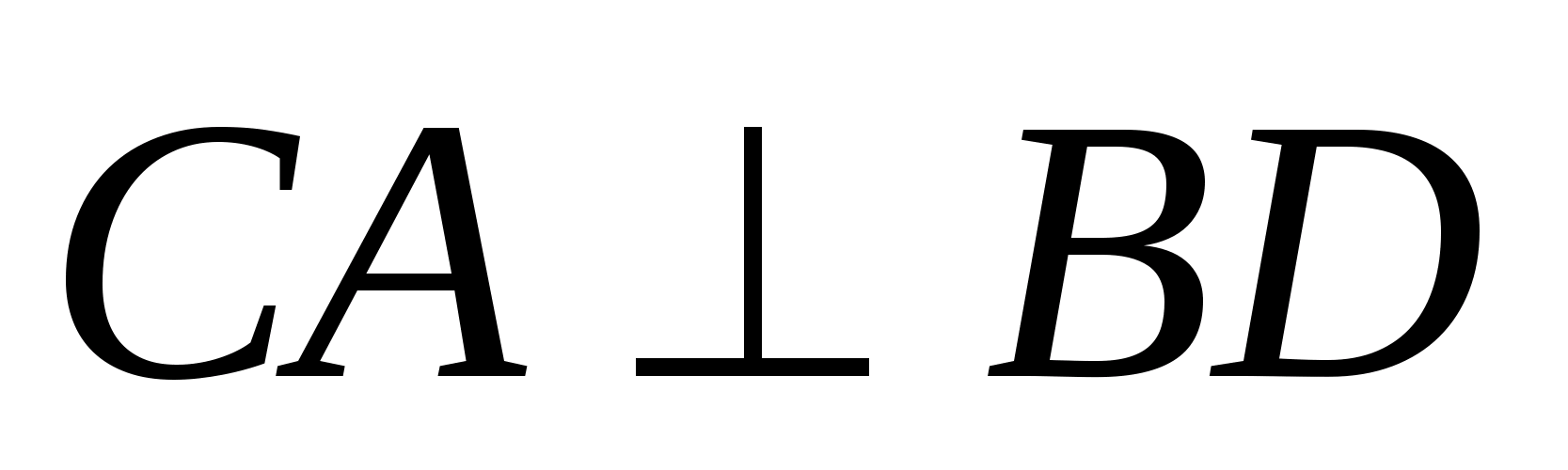
PK ||
CA
и EK
|| BD,
то
и EFPK
— прямоугольник.
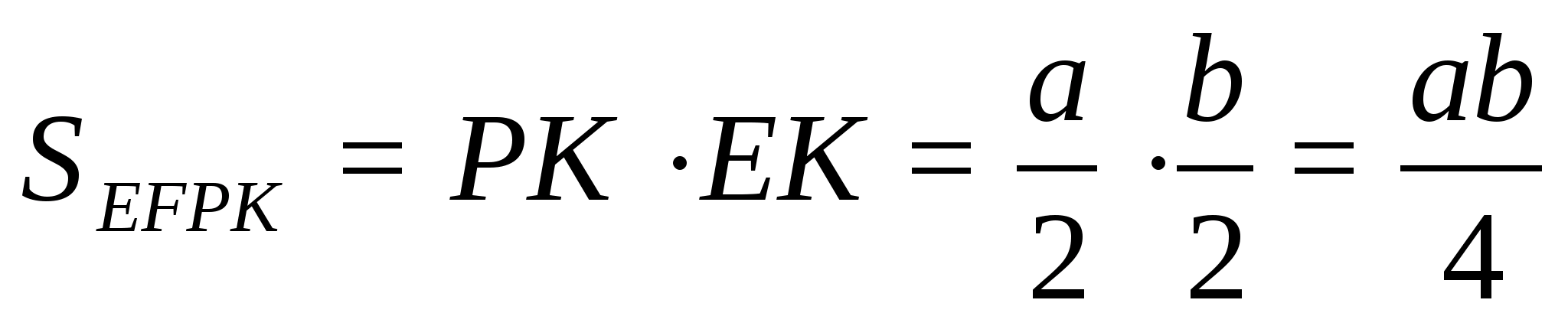
Задача 2 (№692).
Основанием пирамиды
является прямоугольный треугольник с
катетами a
и b.
Каждое её боковое ребро наклонено к
плоскости основания под углом φ.
Найдите объём пирамиды
Решение:
ABCD — пирамида,
угол ABC —
прямоугольный,
AC = b, BC = a, углы
DAO, DBO, DCO равны
. Найдем
V>DABC0>.
1) ∆DAO=∆ADC=∆DBO
по катету
и острому углу, значит
AO=OC=OB=R окружности,
описанной около
∆ABC. Т.к.
∆ABC — прямоугольный,
то
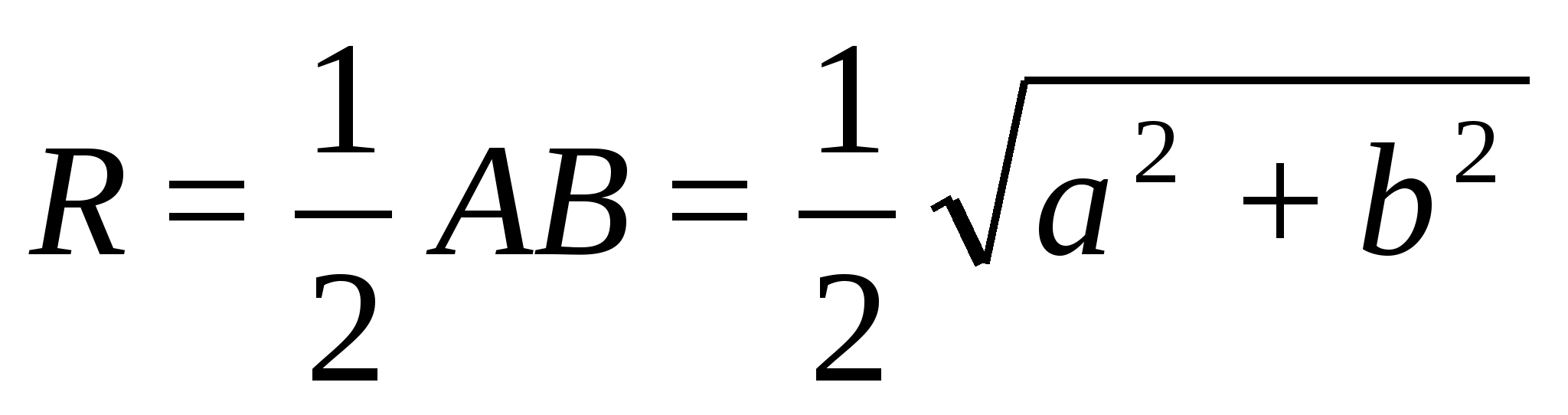
2) Из ∆DOC:
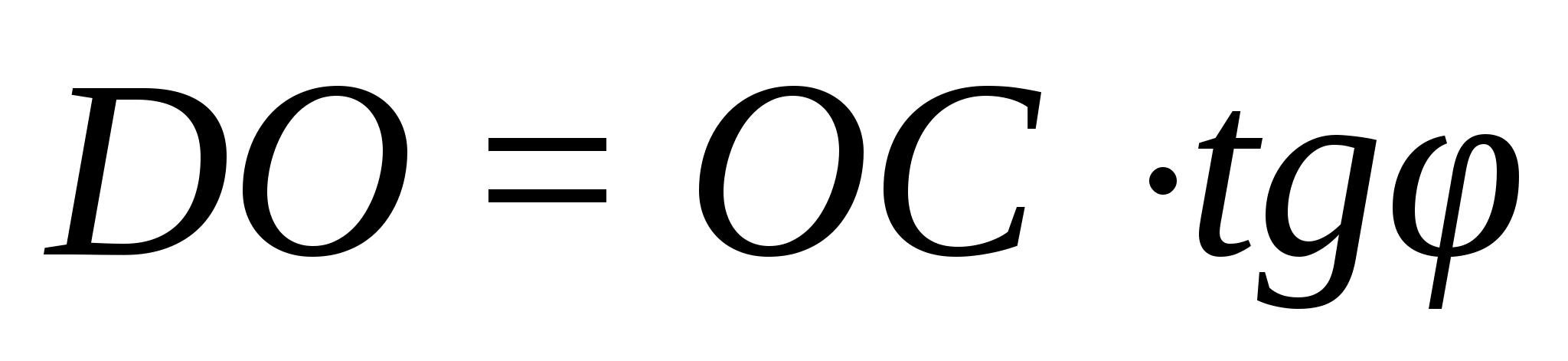
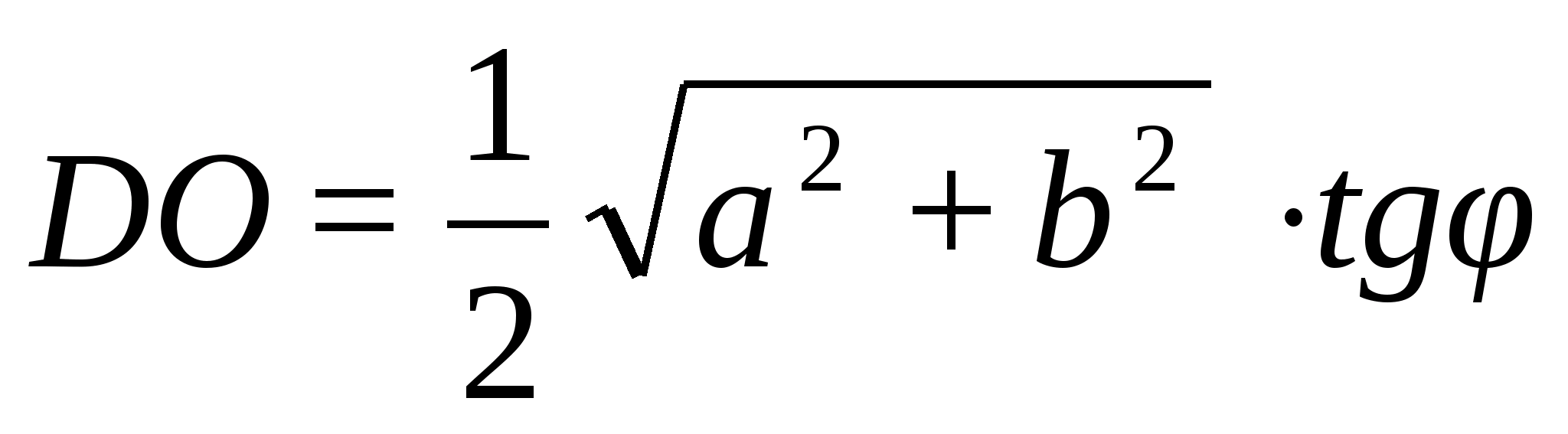
3)
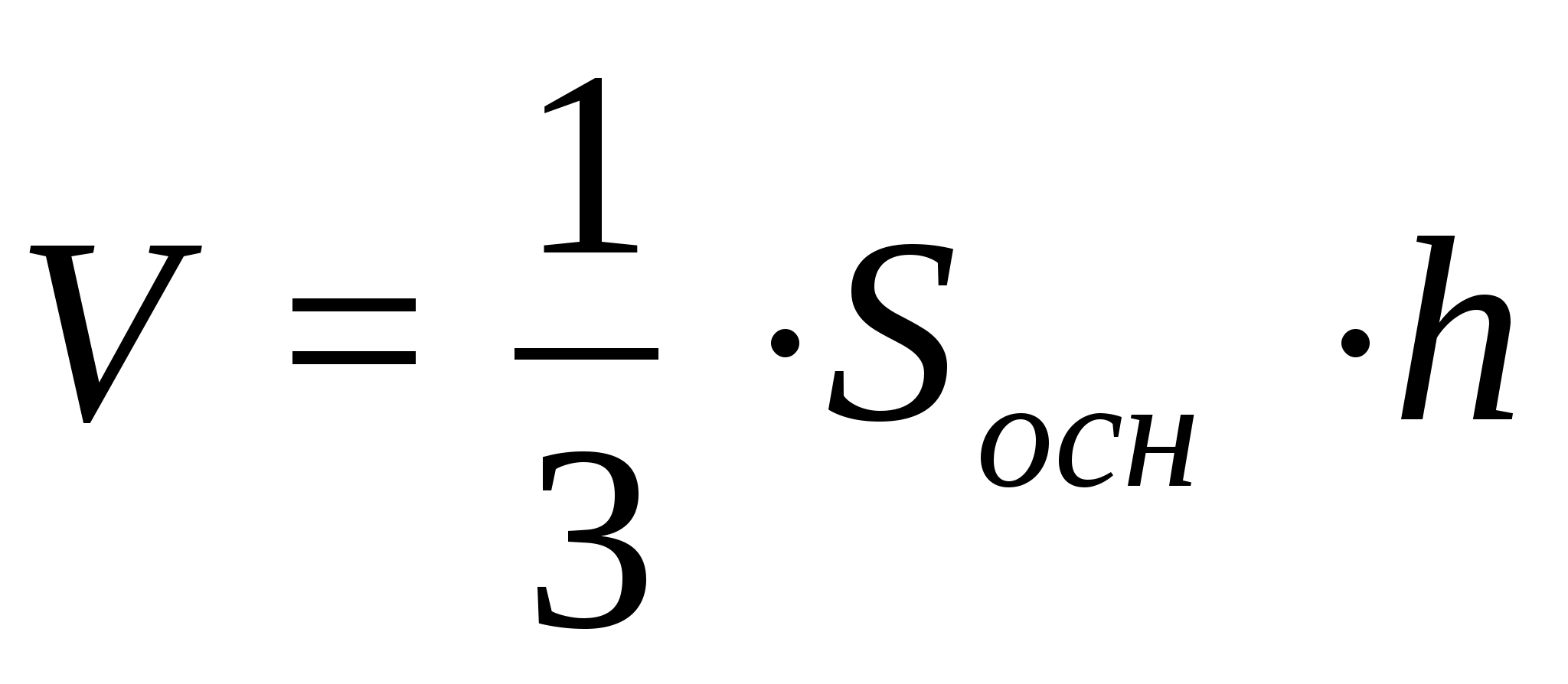
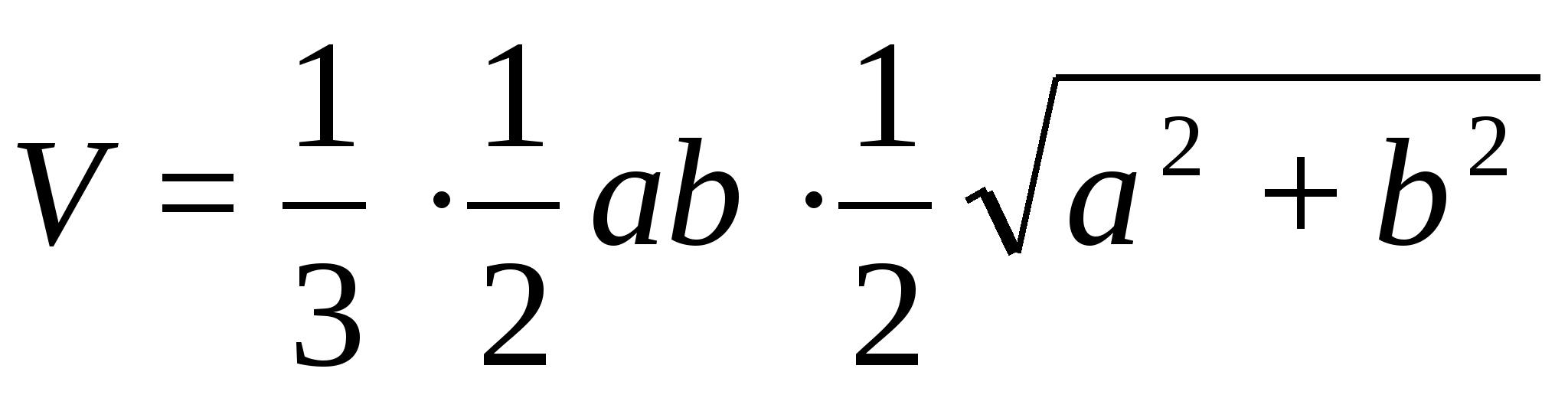
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 7-11 классов
Погорелова А.В.
В другом базовом
учебнике А.В. Погорелова и др.
теоретический
материал в той или иной степени касающийся
темы «Тетраэдр» содержится в пунктах
176-180, 186, 192, 199, 200.
В пункте 180 “Правильные
многогранники” содержится определение
понятия «правильный тетраэдр» (“Тетраэдр
представляет собой треугольную пирамиду,
у которой все рёбра равны”), доказательство
некоторых свойств и теорем о пирамиде
проиллюстрировано чертежами тетраэдра.
Однако в данном учебном пособии акцент
на изучении фигуры не ставится, и в этом
смысле его информативность (касательно
тетраэдра) можно оценить как низкую.
Практический же материал учебника
содержит удовлетворительное количество
заданий, касающихся пирамиды, в основании
которой расположен треугольник (что по
сути и есть тетраэдр). Приведём примеры
решения некоторых задач.
Решение задач.
Задача 1 (№ 41 из пункта
«Многогранники»).
Основание пирамиды
— равнобедренный треугольник, у которого
основание равно 12 см, а боковая сторона
— 10 см. Боковые грани образуют с основанием
равные двугранные углы, содержащие по
45°. Найдите высоту пирамиды.
Решение:
Проведем перпендикуляр
SO к плоскости
основания и перпендикуляры
SK, SM и
SN к сторонам
ΔABС. Тогда
по теореме о трех перпендикулярах
OK
ОМ
и ON
Тогда,

=

=

= 45° — как
линейные углы данных двугранных углов.
А следовательно, прямоугольные
треугольники SKO,
SMO и
SNO равны
по катету и острому углу.
Так что
OK=OM=ON, то
есть точка
О является
центром окружности, вписанной
в
ΔАВС.
Выразим площадь
прямоугольника
АВС:
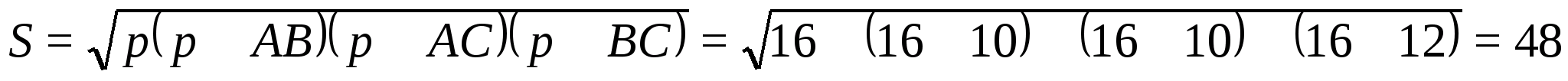
С другой стороны,
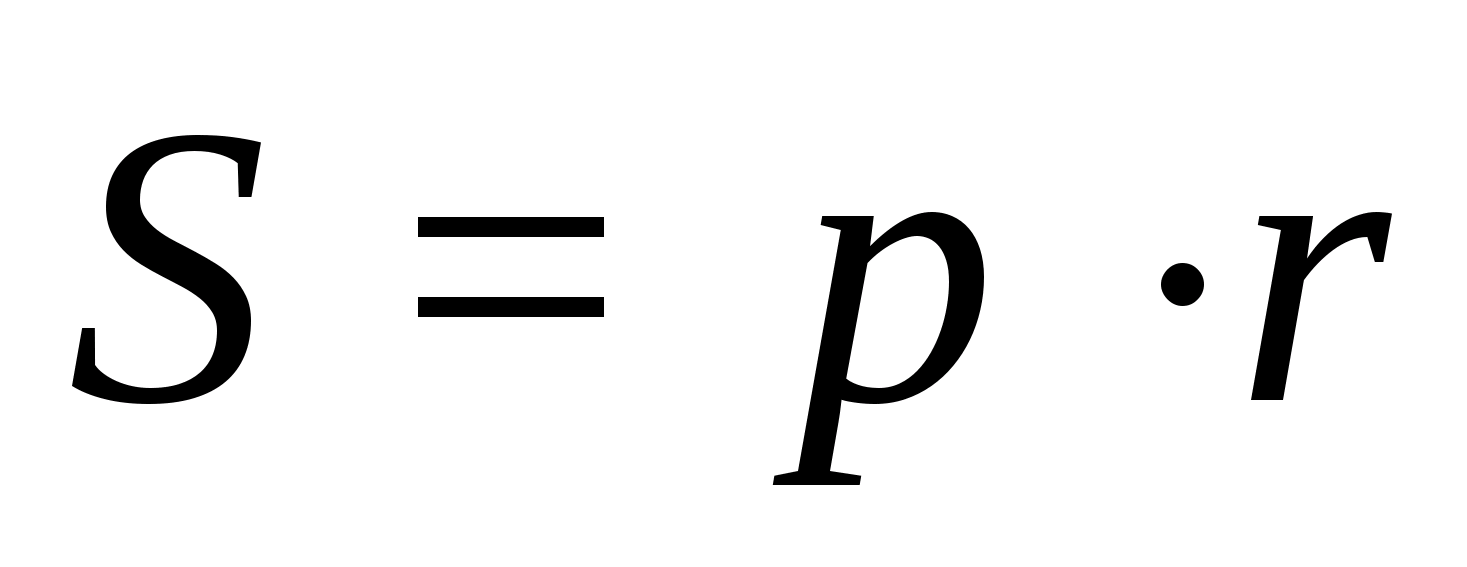
Так что
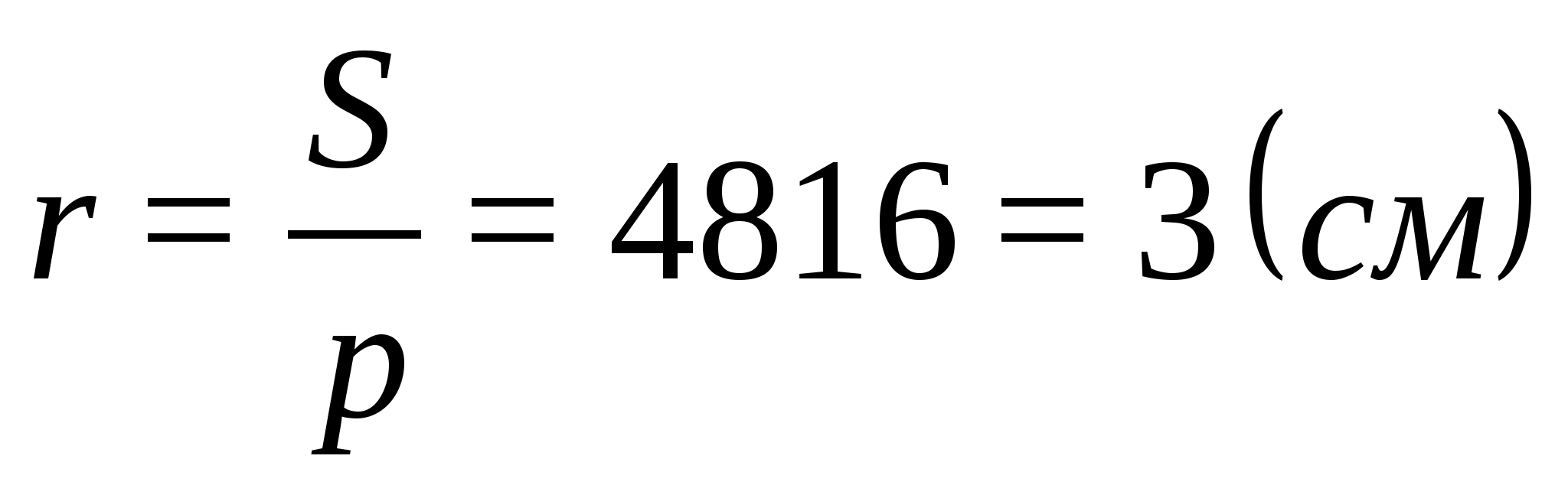
ОК=r=3 см. Так
как в прямоугольном треугольнике
SOK острый
угол равен
45°,
то
ΔSOK является
равнобедренным и
SO=OK=3(см).
Задача 2 (№ 43 из
пункта «Объёмы многогранников»).
Найдите объем
пирамиды, имеющий основанием треугольник,
два угла которого
a и β; радиус
описанного круга
R. Боковые
ребра пирамиды наклонены к плоскости
ее основания под углом
γ.
Решение.
Так как все боковые
ребра пирамиды наклонены к плоскости
основания под одним и тем же углом, то
высота пирамиды
O>1>O
проходит
через центр описанной около основания
окружности. Так что
Далее, в прямоугольном
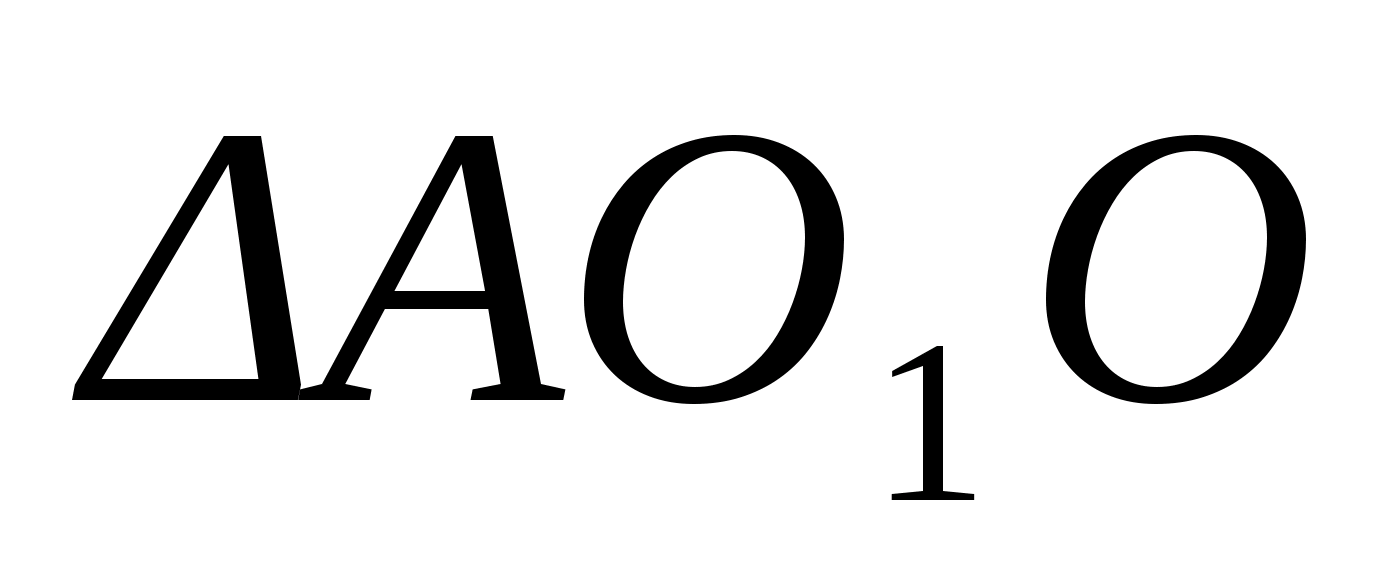
В ΔАВС
Тогда
согласно теореме синусов
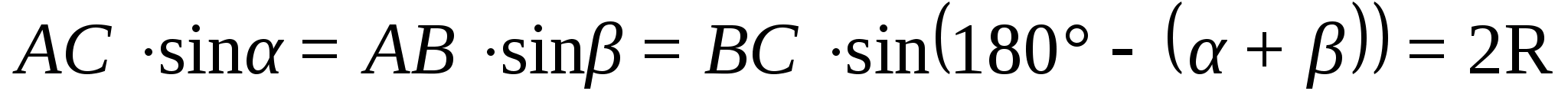
Так что
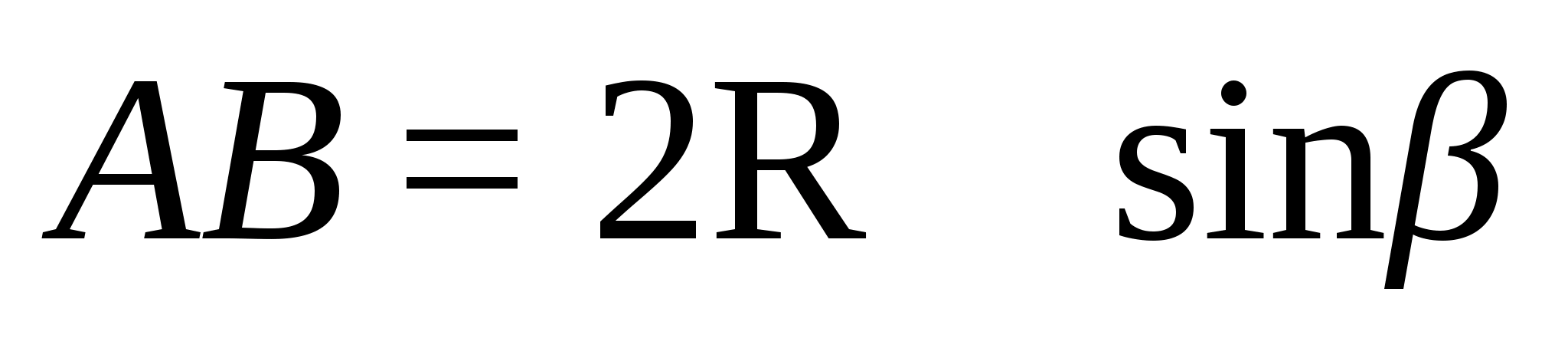
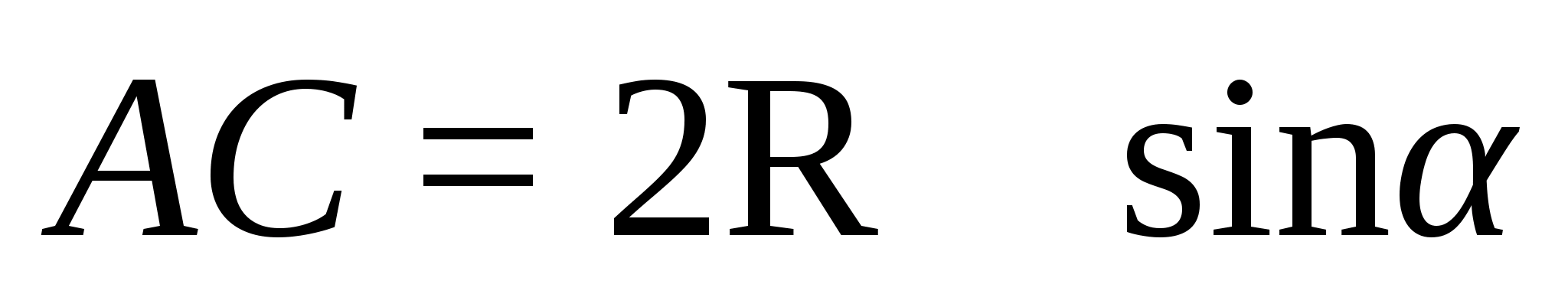
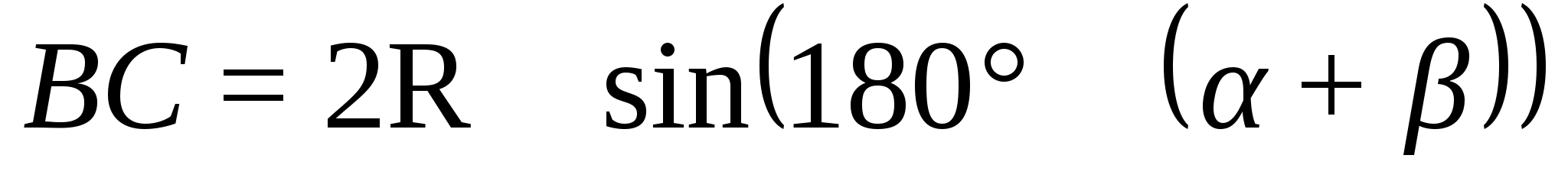
=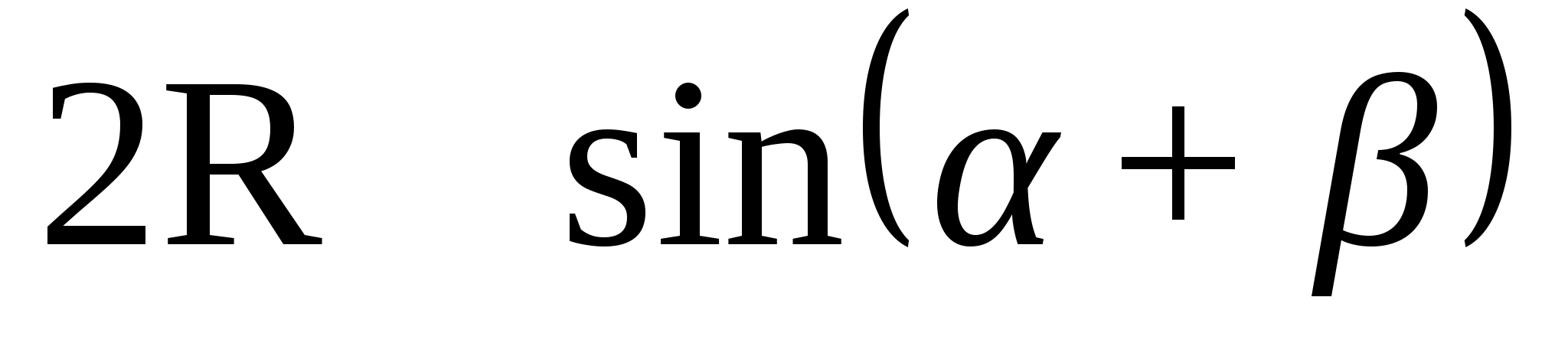
Площадь треугольника
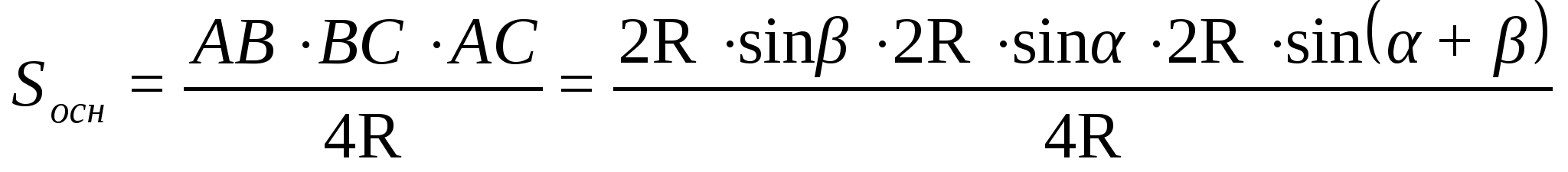
Тогда
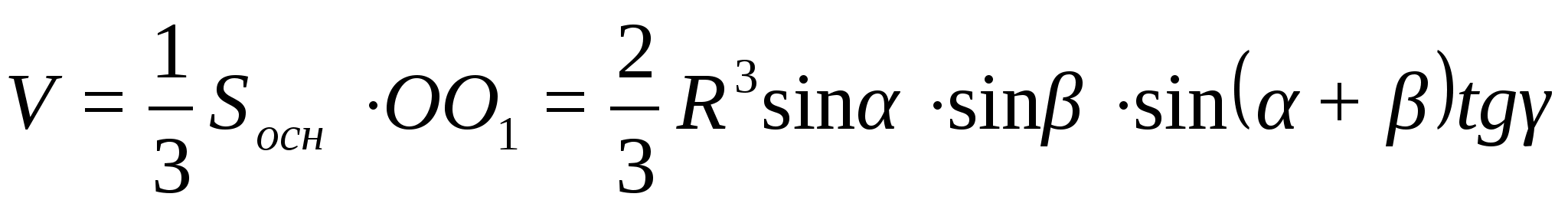
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Александрова А.Д.
Рассмотрим учебное пособие
Александрова А.Д. и др. «Геометрия:
учебник для учащихся 11 кл. с углубленным
изучением математики». Отдельных
параграфов, посвящённых тетраэдру в
этом учебнике нет, однако тема присутствует
в виде фрагментов других параграфов.
Впервые тетраэдр упоминается в
§21.3. В материале параграфа рассматривается
теорема о триангуляции многогранника,
в качестве примера выполняют триангуляцию
выпуклой пирамиды. Само понятие
«многогранник» в учебнике трактуется
двумя способами, второе определение
понятия напрямую связано с тетраэдром:
«Многогранник – это фигура, являющаяся
объединением конечного числа тетраэдров…».
Познания, касающиеся правильной пирамиды
и некоторых аспектов симметрии тетраэдра
можно обнаружить в §23.
В §26.2 описано применение теоремы
Эйлера («о правильных сетях») для
правильных многогранников (в т.ч. для
тетраэдра), а в §26.4 рассматриваются виды
симметрий, характерные для этих фигур.
Формулу для нахождения объёма
пирамиды авторы вводят в задаче №30.1(2),
а площадь боковой поверхности пирамиды
вводится в материале параграфа «Площадь
поверхности конуса и цилиндра» (§32.5).
Также, в учебнике можно найти
информацию о средней линии тетраэдра,
центре масс (§35.5) и классе равногранных
тетраэдров. Движения I
и II
рода демонстрируются в ходе решения
задач о тетраэдрах.
Отличительная особенность
учебника — высокая научность, которую
авторам удалось совместить с доступным
языком и чёткой структурой изложения.
Приведём примеры решения некоторых
задач.
Решение задач.
Задача 1.
В данную правильную
треугольную усечённую пирамиду с боковым
ребром a можно поместить сферу, касающуюся
всех граней, и сферу, касающуюся всех
рёбер. Найдите стороны оснований
пирамиды.
Решение.
Изобразим на чертеже
«полную» пирамиду. Данная пирамида
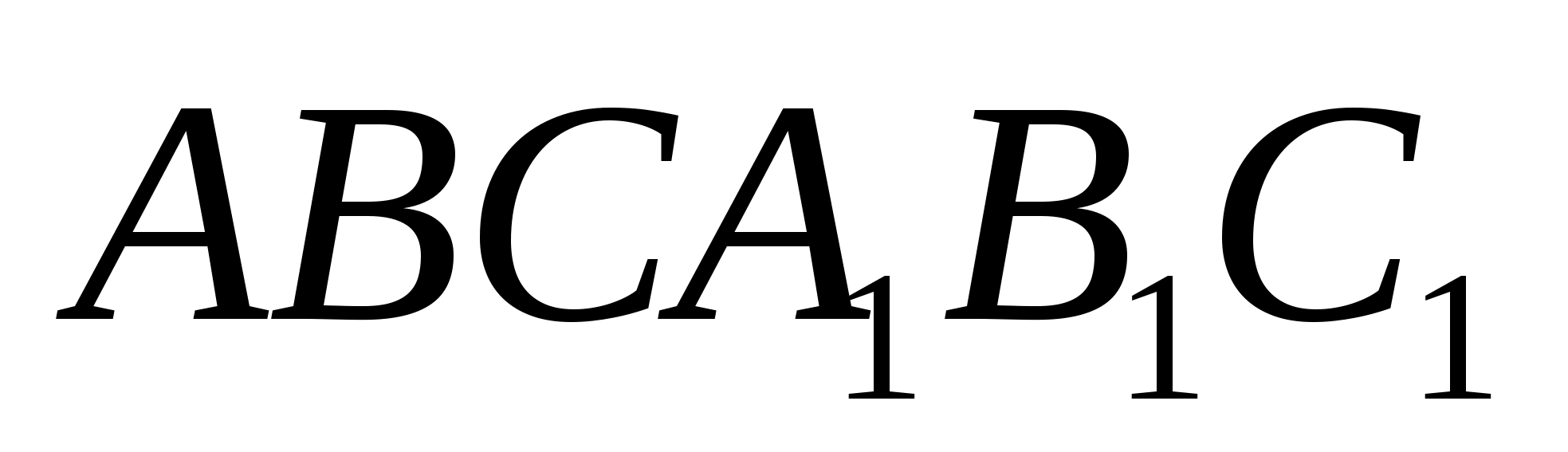
— высота «полной» пирамиды,
— ее часть до верхнего основания
усеченной. Задача сводится к
планиметрической, при этом не надо
рисовать ни одной из данных сфер. Т.к. в
усеченную пирамиду можно вписать сферу,
касающуюся всех ребер, то в её боковую
грань можно вписать окружность. Обозначим
(для удобства деления пополам) и для
описанного четырехугольника
получим, что
откуда
Из существования
вписанного шара следует, что существует
полуокружность, расположенная в трапеции
(
— апофема «полной» пирамиды) так, что
ее центр лежит в середине
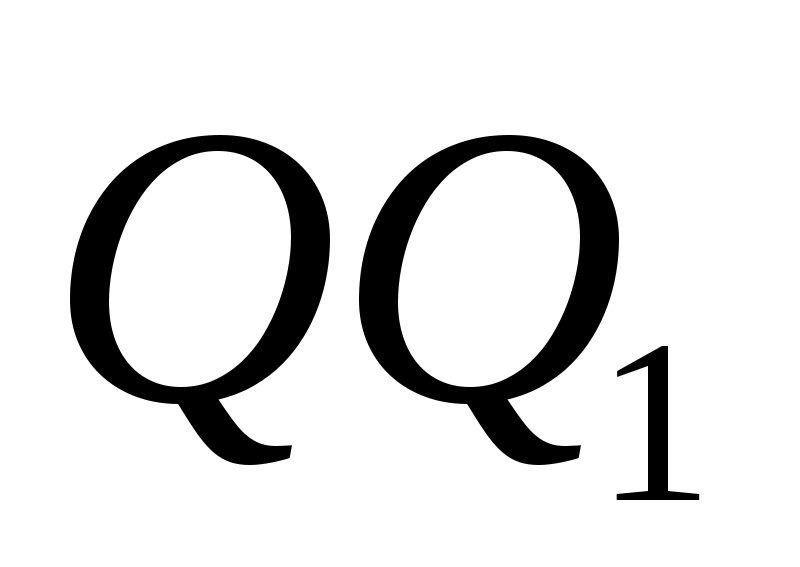
а сама она касается остальных трёх
сторон трапеции.
— центр шара,
и
— точки касания. Тогда
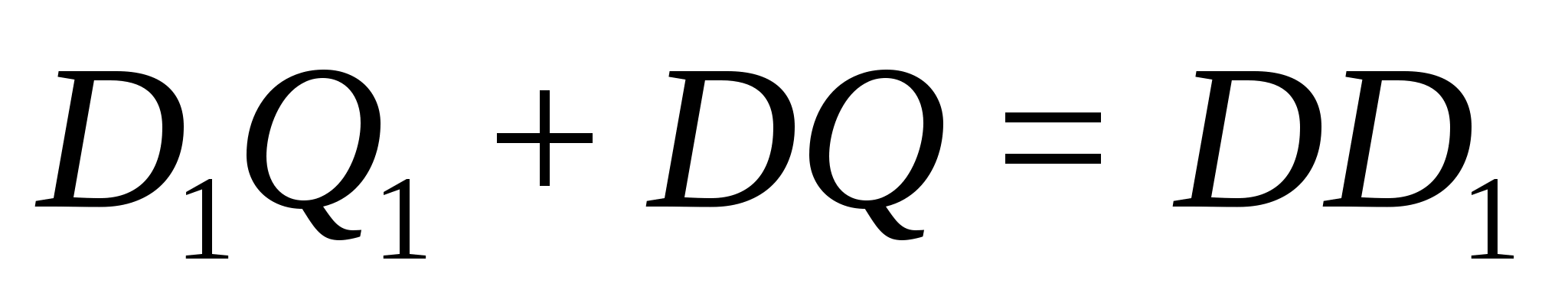
Выразим эти величину через
и
Из
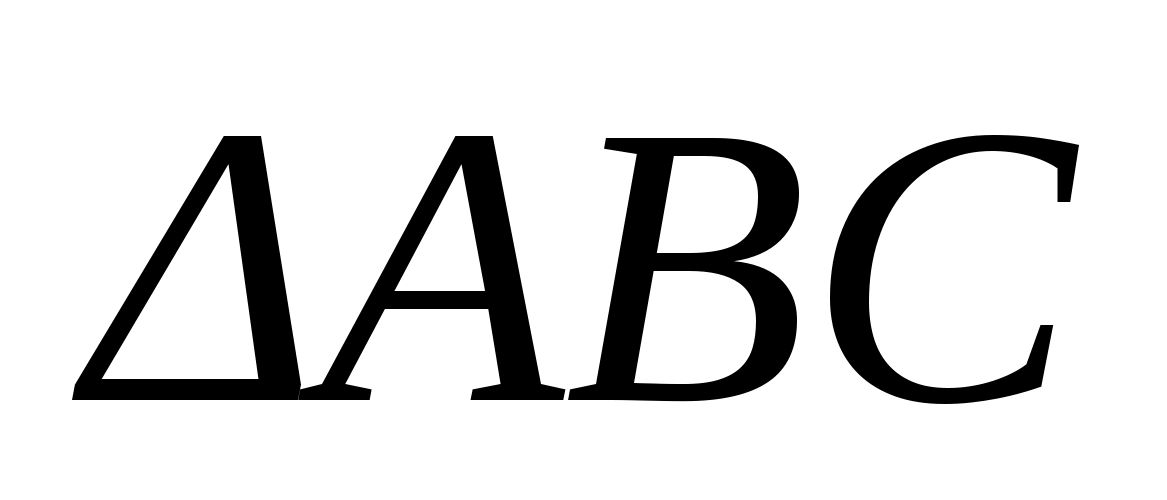
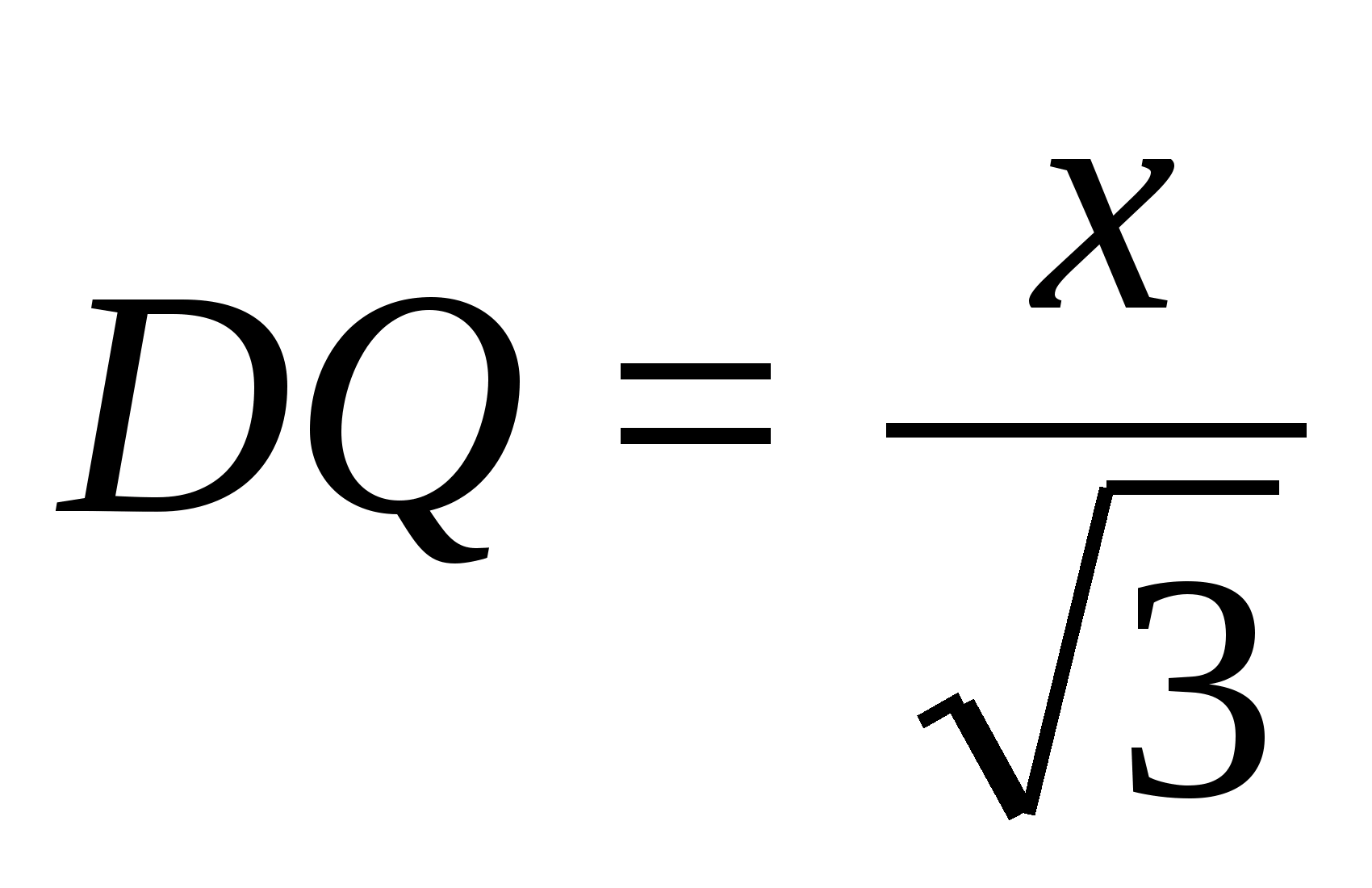
Из

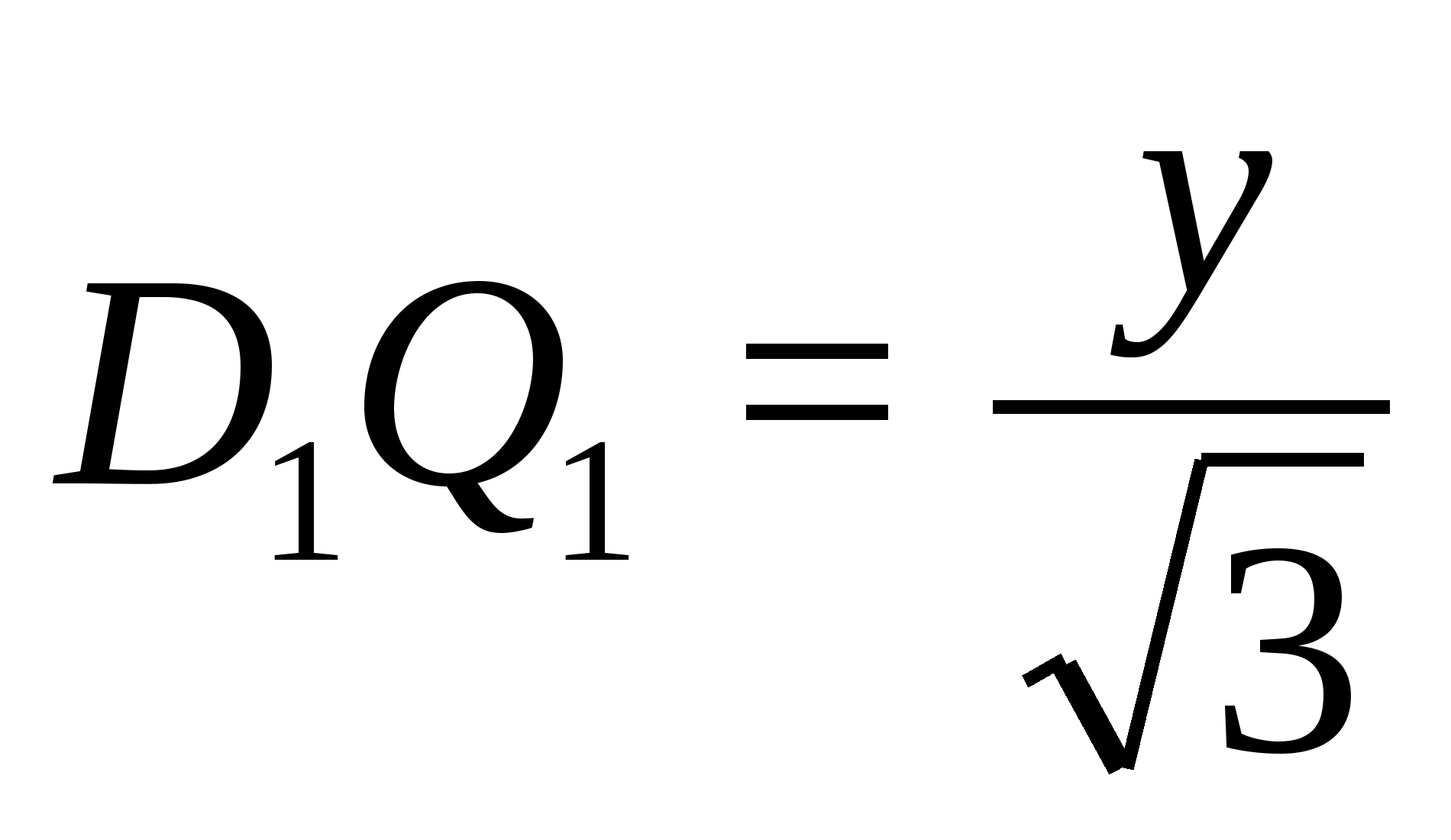
Из трапеции
Получаем уравнение:
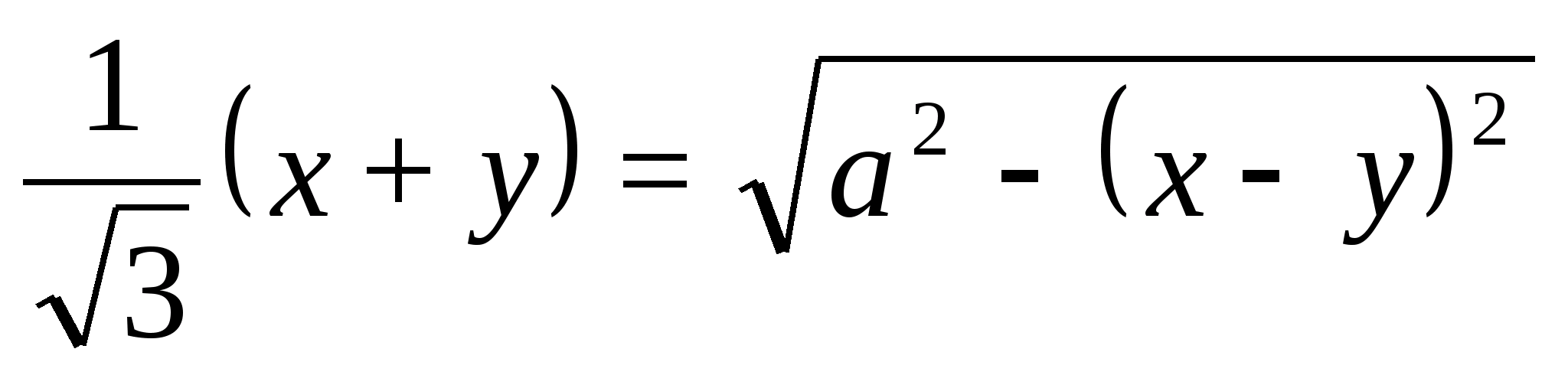
Решив систему
уравнений (1) и (2), получим, что стороны
оснований равны
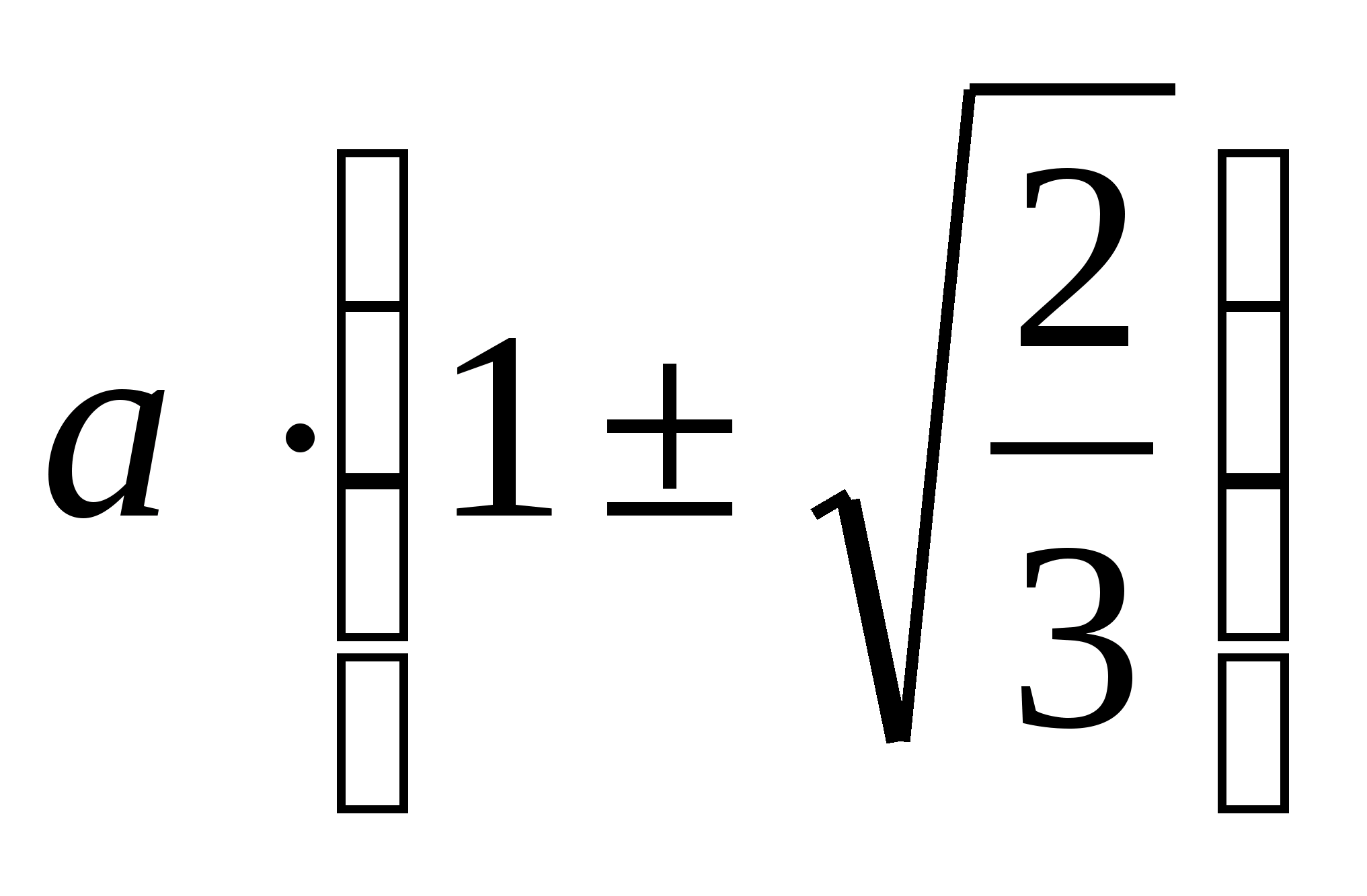
Задача 2.
Внутри правильного
тетраэдра с ребром a
расположены четыре равные сферы так,
что каждая сфера касается трех других
сфер и трех граней тетраэдра. Найти
радиус этих сфер.
Решение.
— данный тетраэдр,
— его высота,
— центры сфер,
— точка пересечения прямой
с плоскостью
Заметим, что центры равных сфер
касающихся плоскости
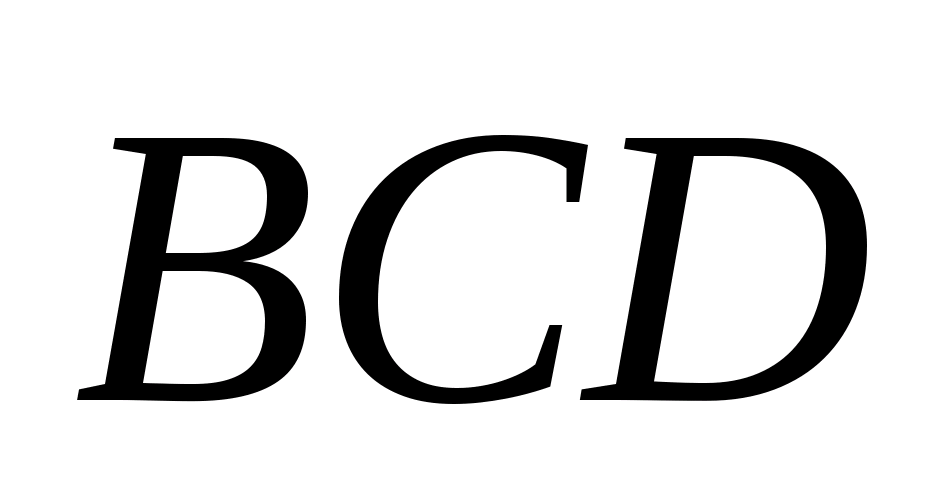
удалены от нее на равные расстояния,
каждое из которых равно радиусу шара
(обозначием его как x).
Значит плоскости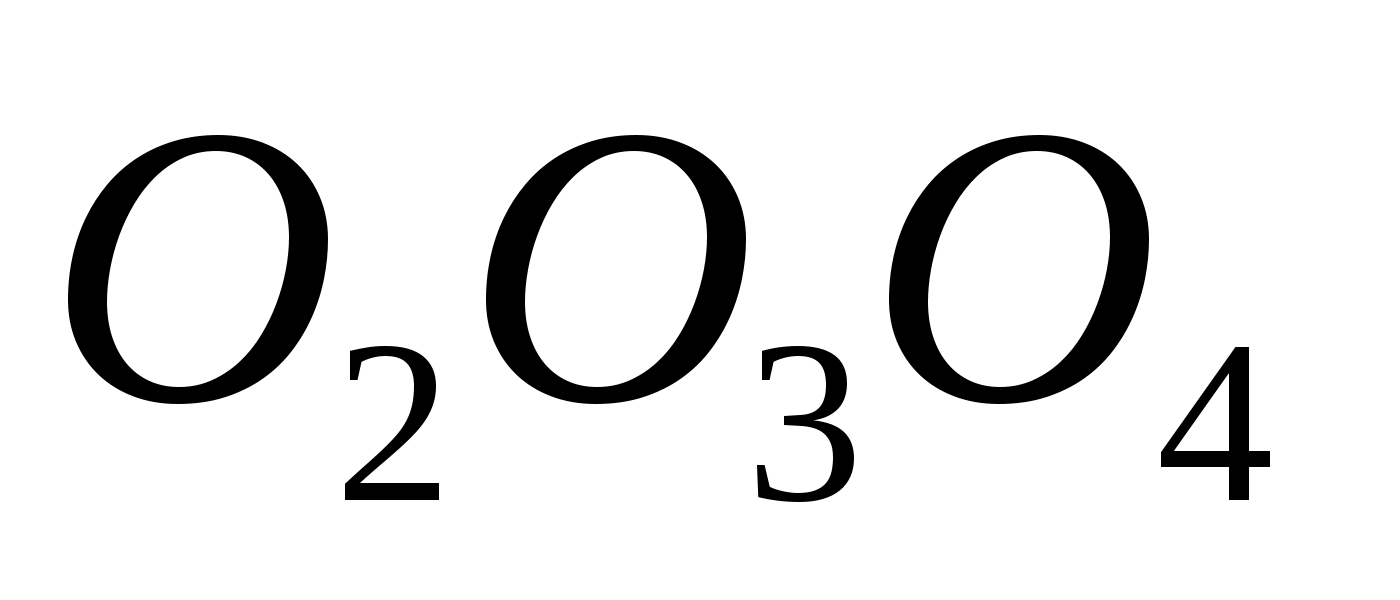
параллельны, а потому
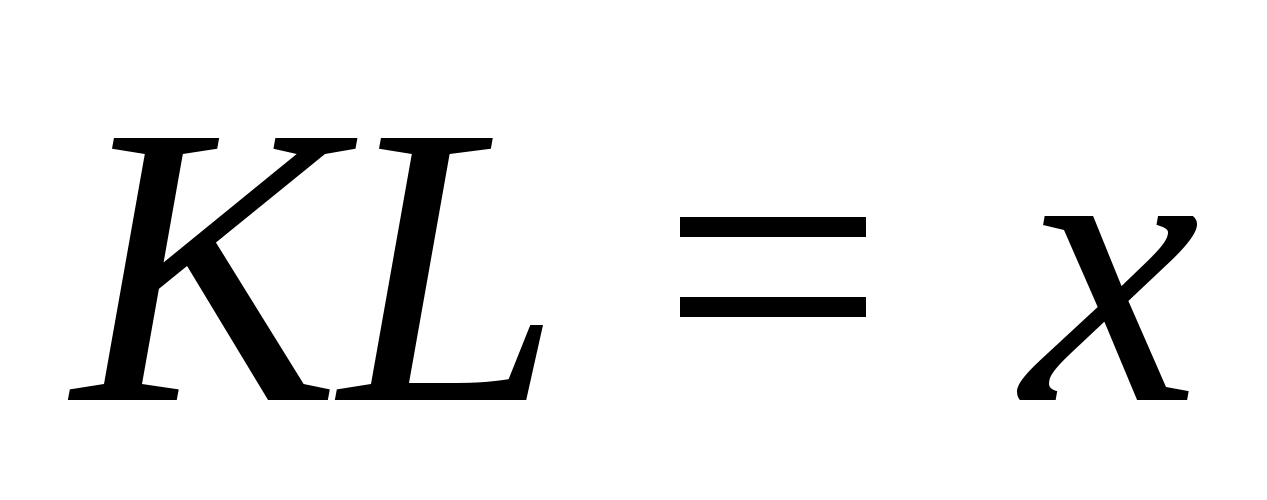
Далее, каждая пара
шаров касается между собой, а потому
расстояние между центрами равно сумме
их радиусов, то есть 2x.
Имеем:
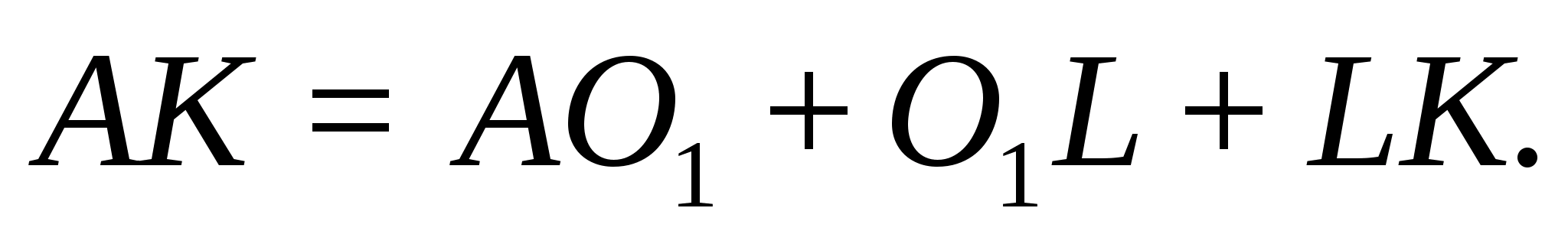
Но
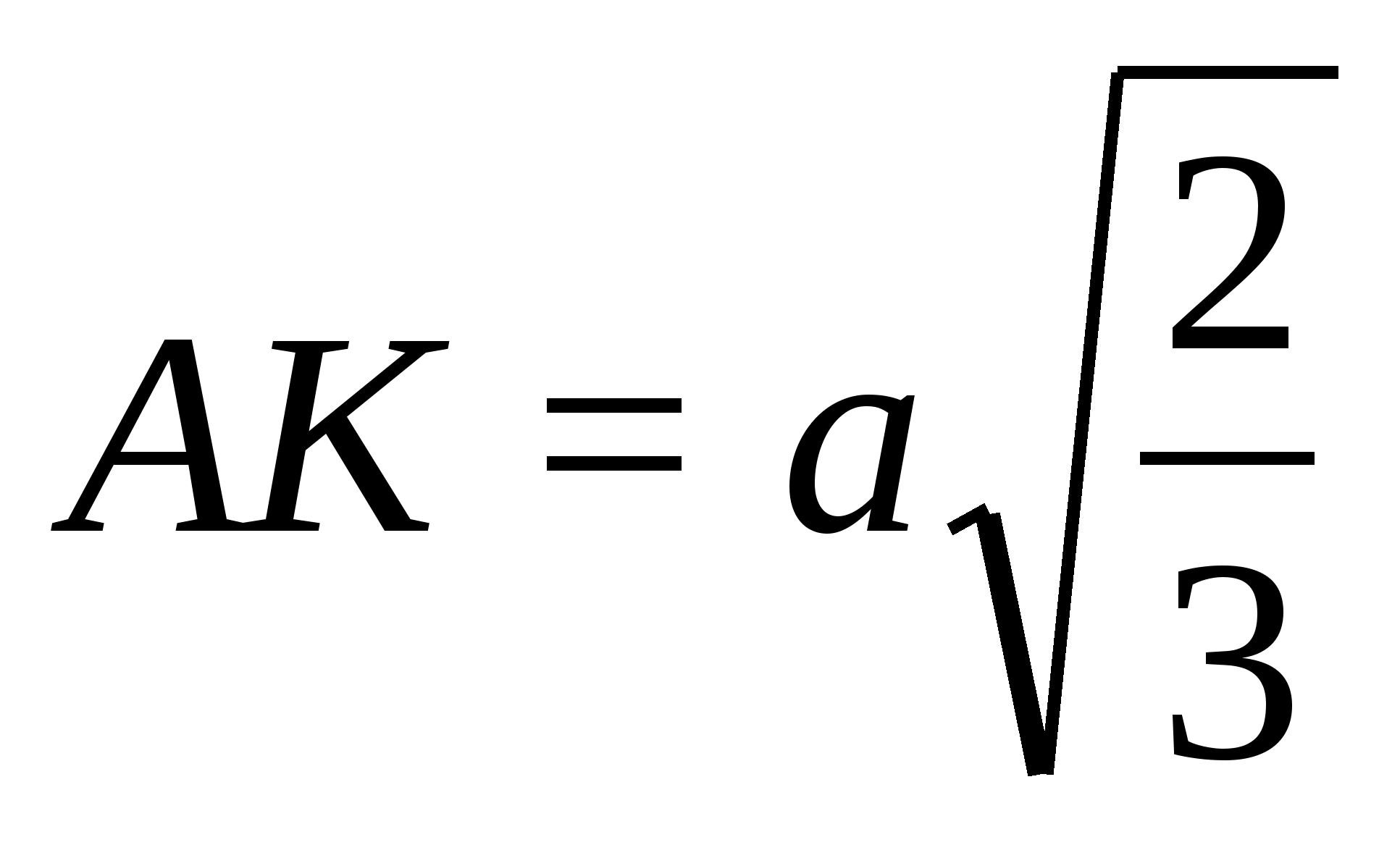
высота правильного тетраэдра с ребром
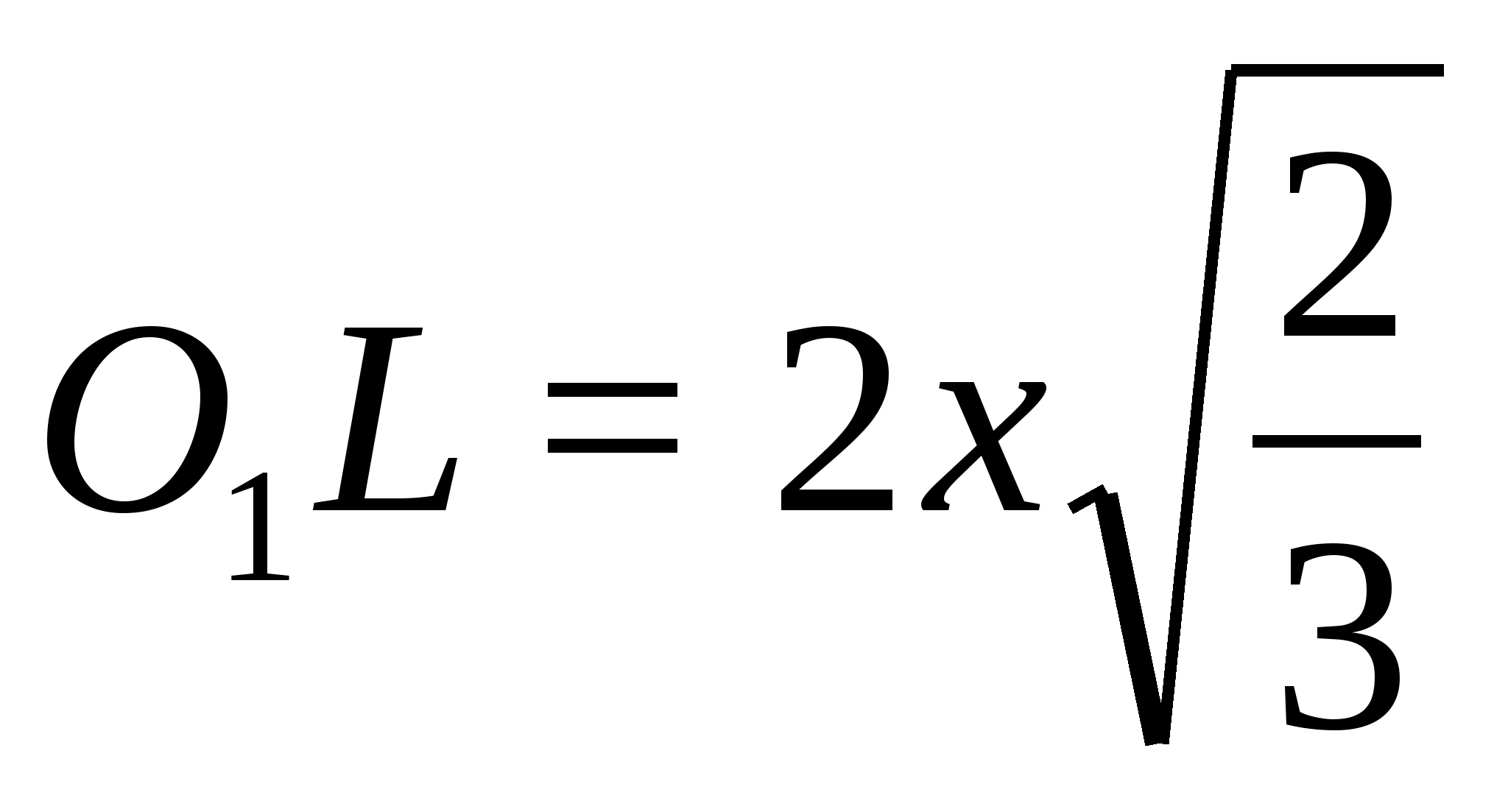
высота правильного тетраэдра с ребром
2x;
Осталось выразить
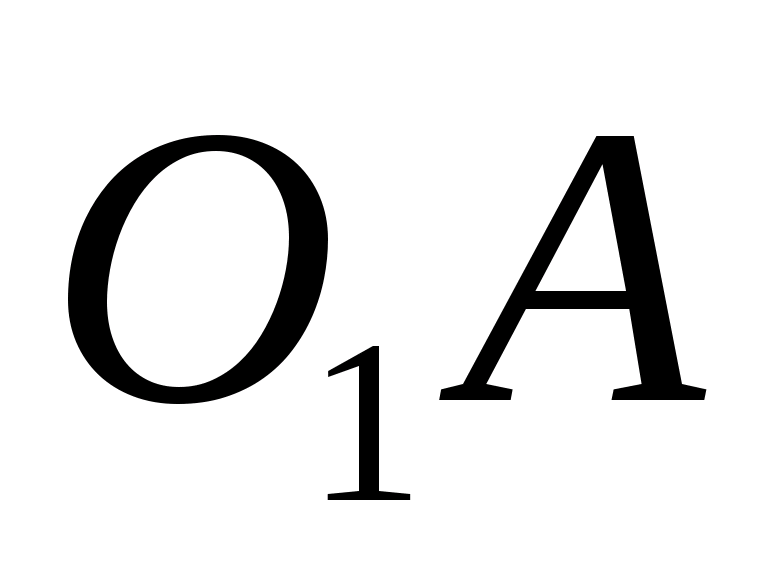
Заметим, что точка
находится внутри трехгранного угла и
удалена от его граней на расстояние
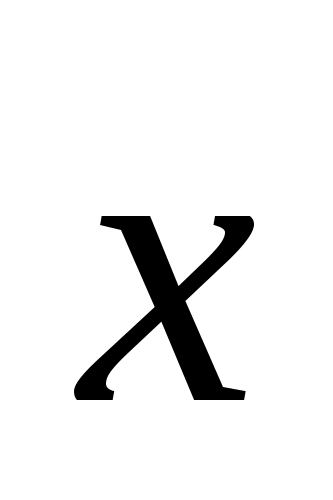
а плоские углы трехгранного угла равны

Не сложно получить то, что
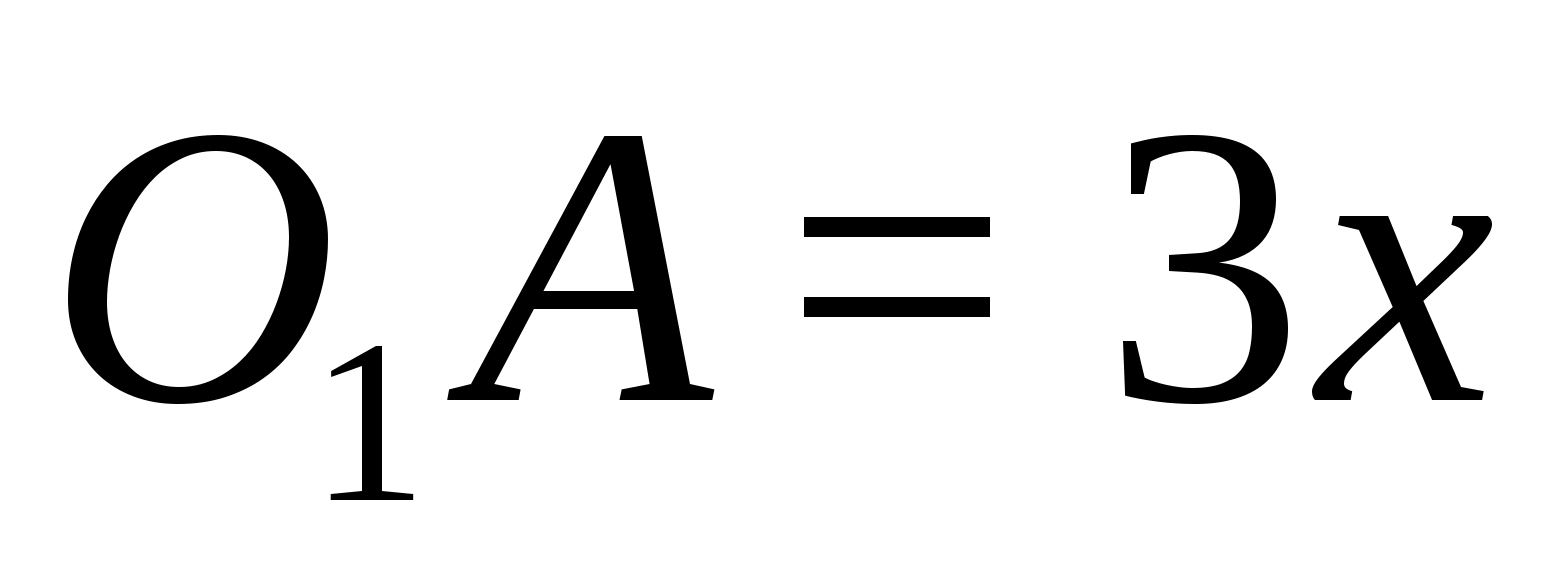
Приходим к уравнению:
откуда после упрощений получаем
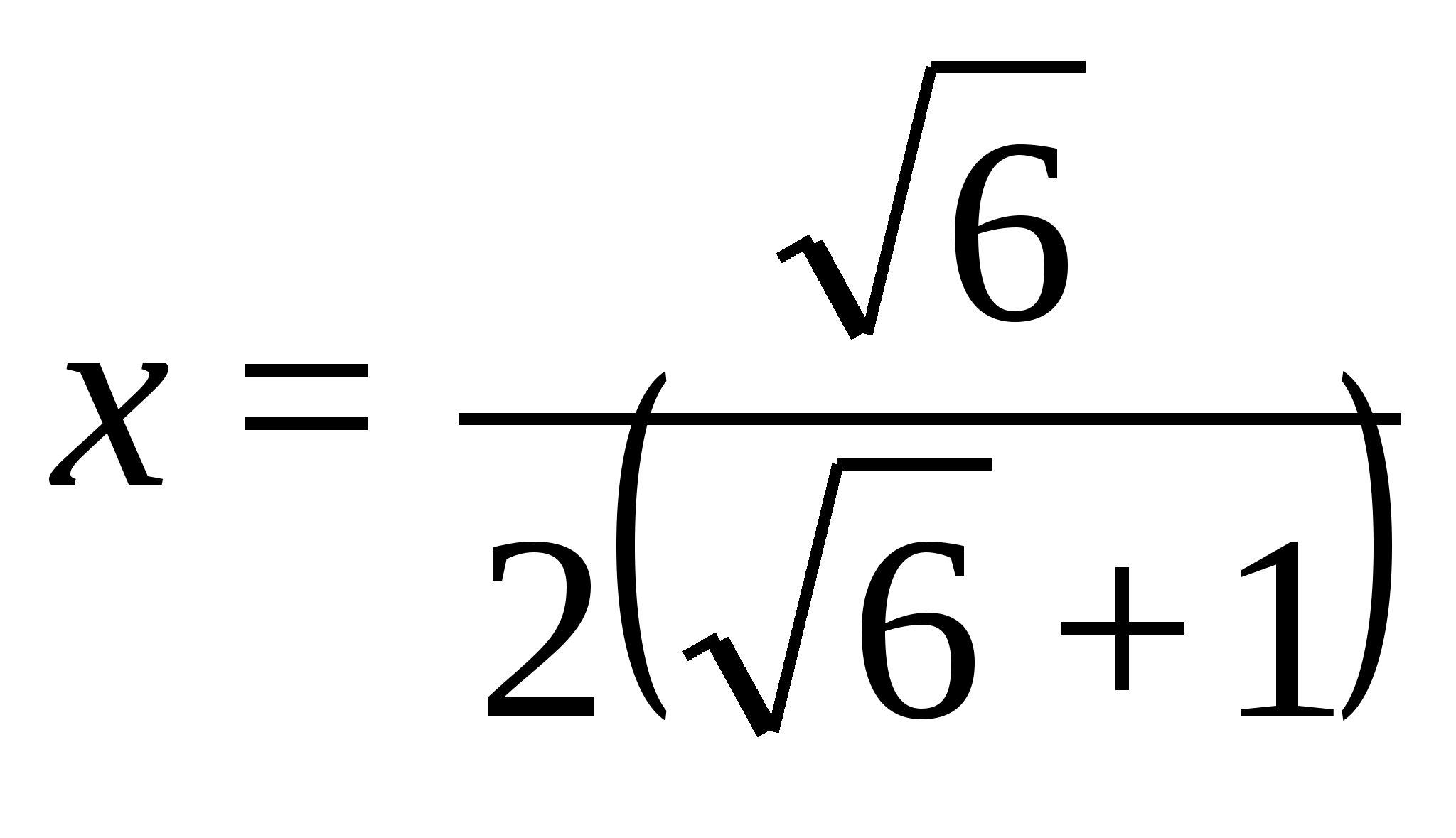
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М.
Изложению темы «Тетраэдр» в
учебнике для 10-11 классов гуманитарного
профиля Смирновой И.М. посвящены
следующие занятия: 18,
19, 21, 22, 28-30, 35.
После изучения
теоремы о том, что «Всякий
выпуклый многогранник может быть
составлен из пирамид с общей вершиной,
основания которых образуют поверхность
многогранника» рассматривается теорема
Эйлера для некоторых таких многогранников,
в частности, выполнение условий теоремы
рассмотрено и для треугольной пирамиды,
которая, в сущности, и есть тетраэдр.
Учебник интересен
тем, что в нём рассматривается топология
и топологически правильные
многогранники(тетраэдр,
октаэдр, икосаэдр, куб, додекаэдр),
чье существование обосновывается при
помощи той же теоремы Эйлера.
Помимо этого в
учебнике приведено определение понятия
«правильная пирамида»; рассматриваются
теоремы о существовании вписанной и
описанной сфер тетраэдра, некоторые
свойства симметрии, касающиеся тетраэдра.
На заключительном занятии (35) приводится
формула нахождения объёма треугольной
пирамиды.
Для данного учебного
пособия характерен большой объем
иллюстративного и исторического
материала, а также небольшой объём
практического материала, обусловленный
направленностью учебника. Рассмотрим
также учебник Смирновой И.М. и др. для
10-11 классов естественно-научного профиля.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М. и др.
От предыдущего учебного пособия
данное отличается компоновкой тем и
уровнем сложности предлагаемых к решению
задач. Отличительной особенностью
изложения материала является деление
его на «семестры», которых в учебнике
четыре. Тетраэдр упоминается в самом
первом параграфе («Введение в стереометрию»)
, понятие «пирамида» определяется в §3.
Как и в предыдущем учебнике
практический материал дополнен заданиями
с развёрткой стереометрических фигур.
В материале §26 можно найти теорему о
сфере, вписанной в тетраэдр. Остальной
теоретический материал, касающийся
тетраэдра, фактически совпадает с
материалами учебника, охарактеризованного
выше.
Решение задач.
Задача 1.
Найдите кратчайший
путь по поверхности правильного тетраэдра
ABCD
соединяющий
точки E
и F,
расположенные на высотах боковых граней
в 7 см от соответствующих вершин тетраэдра.
Ребро тетраэдра равно 20 см.
Решение.
Рассмотрим развертку
трех граней тетраэдра. Кратчайшим путем
будет отрезок, соединяющий точки E
и F.
Его длина равна
20 см.
Задача 2.
В основании пирамиды
лежит прямоугольный треугольник, один
из катетов которого равен 3 см, а прилежащий
к нему острый угол равен 30 градусам. Все
боковые ребра пирамиды наклонены к
плоскости основания под углом в 60
градусов. Найдите объем пирамиды.
Решение.
Площадь треугольника
ABC равна
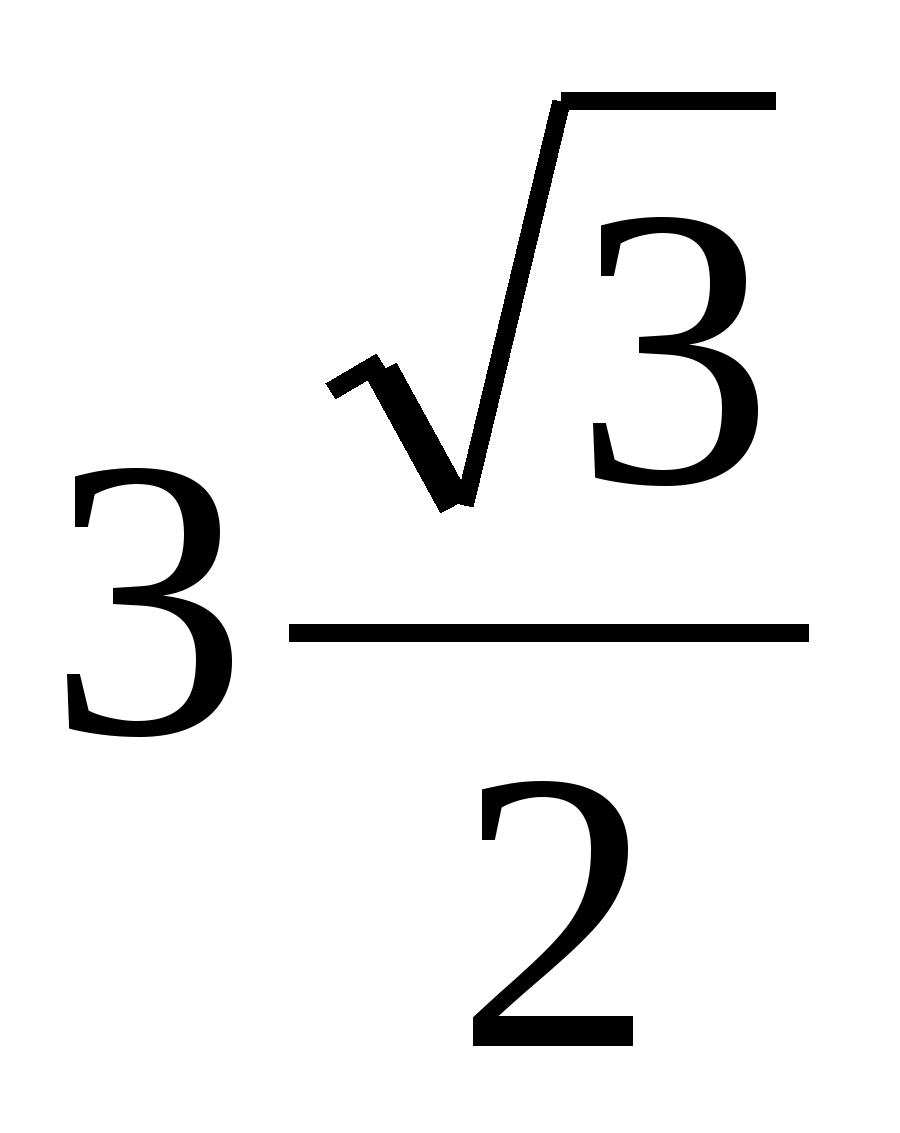
Основанием высоты
служит середина
Треугольник SAC — равносторонний.
Отсюда
и, следовательно,
объем пирамиды равен
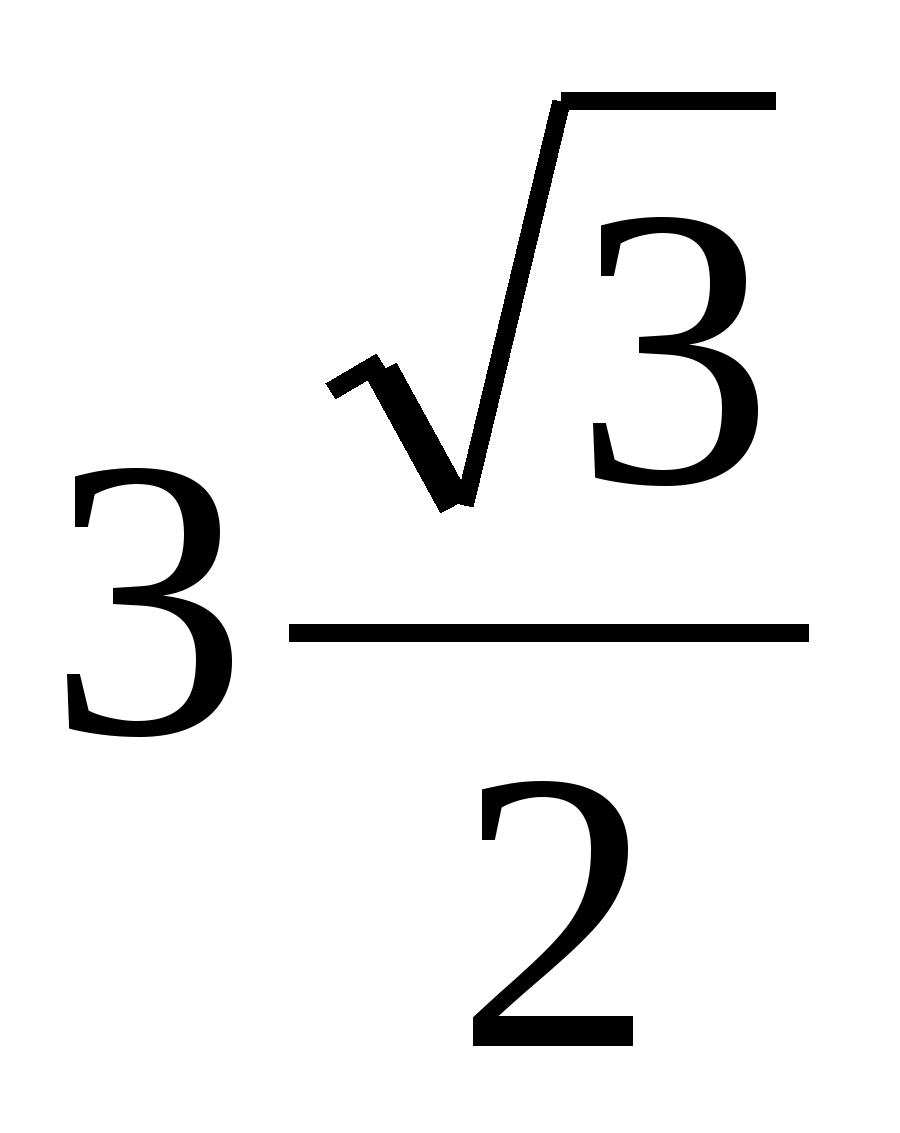
Вывод.
Отличительной
особенностью учебника Атанасяна Л.С. и
др. является то, что изучение тетраэдра
начинается достаточно рано, материал
разбросан по всему курсу и представлен
в различных уровнях сложности. В учебнике
Погорелова А.В. материал расположен
компактно, понятие «тетраэдр» как и
понятия других пространственных фигур,
вводится достаточно поздно (в конце 10
класса), практический материал,
представленный в учебнике, небольшого
объема. В учебнике Смирновой И.М. и др.
теоретический материал, как и практический
имеет небольшой объем, практический
задания низкого уровня сложности,
учебник отличается большим объём
материала из истории математики. В
учебнике Александрова А.Д. и др. уровень
сложности материала выше, сам материал
разнообразнее, множество практических
заданий содержит некоторую часть теории,
имеются экстремальные задачи и задачи
в виде вопросов, что выгодно выделяет
его на фоне остальных.
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Интеллект — это способность к
обучению или пониманию, которая присуща
всем людям. Одни люди обладают ею в
большей степени, другие — в меньшей,
однако у каждого человека в течение
жизни эта способность сохраняется
практически без изменений. Именно
благодаря интеллекту мы способны
правильно действовать и учиться на
своих ошибках.
В психологии интеллект определяется,
как способность воспринимать знания и
использовать их в других, принципиально
новых ситуациях. В условиях тестирования
можно определить, насколько успешно
адаптируется человек к необычным
ситуациям. Определение уровня общего
интеллектуального развития посредством
теста – довольно трудная и ёмкая по
времени работа, поэтому в тексте данной
работы будет использоваться часть
методики тестирования интеллекта,
отвечающая на вопрос об уровне развития
пространственного мышления. Пространственное
мышление – это
специфический вид мыслительной
деятельности, которая имеет место в
решении задач, требующих ориентации в
практическом и теоретическом пространстве
(как видимом, так и воображённом). В
своих наиболее развитых формах это
мышление образцами, в которых фиксируются
пространственные свойства и отношения.
Оперируя исходными образами, созданными
на различной наглядной основе, мышление
обеспечивает их видоизменение,
трансформацию и создание новых образов,
отличных от исходных.
Используемый тест («Мини-тест
уровня развития пространственного
мышления» из «Первого теста на коэффициент
развития интеллекта» Ф. Картера, К.
Рассела) универсален для всех возрастных
групп и занимает малый объём времени
(30 минут). Текст теста и его ключи можно
найти в «Приложении №1» к диплому.
2014-06-07
Доказать, что существует тетраэдр $ABCD$, все грани которого являются подобными прямоугольными треугольниками с острыми углами при вершинах А и В. Определить, какое из ребер этого тетраэдра наибольшее, а какое — наименьшее, и найти длину наименьшего ребра, если длина наибольшего равна 1.
Решение:
Предположим, что указанный в условии задачи тетраэдр ABCD существует, и докажем, что ребро АВ является наибольшим, а ребро CD — наименьшим. Из условия задачи следует, что каждый из углов АСВ, ADB, а также один из углов ACD или ADC, скажем угол ACD, прямой (рис.). Положим $angle BAC = phi$. Тогда $angle ABD = phi$, поскольку в противном случае $angle BAD = phi$ и AC = AD, что невозможно (ибо AD — гипотенуза треугольника ACD). Аналогично, $angle CDA = phi$, (иначе $angle CAD = phi$ и AB = AD, что невозможно). Поэтому имеем равенства
$BD = AC = AB cos phi$,
$BC = AD = AB sin phi$,
$CD = AD cos phi = AB sin phi cos phi$,
$AC = AD sin phi = AB sin^{2} phi$,
откуда, в частности, получаем, что
$cos phi = sin^{2} phi = 1 — cos^{2} phi$,
т. е.
$phi = arccos : ((sqrt{5} — 1)/2)$.
Таким образом, наибольшее ребро $AB$ имеет длину 1, а наименьшее ребро $CD$ — длину $sin phi cos phi = sqrt{ cos phi} cos phi = ((sqrt{5} — 1)/2)^{3/2}$. Для доказательства существования такого тетраэдра достаточно заметить, что если рассмотреть тетраэдр ABCD с ребрами
$CA = (sqrt{5} – 1)/2, CB = ((sqrt{5} — 1)/2)^{1/2}, CD = ((sqrt{5} — 1)/2)^{3/2}$
и плоскими углами
$angle BCA = angle DCA = 90^{circ}, angle BCD = arcos ((sqrt{5} — 1)/2)$,
то
$AB = 1, AD = CB, BD = AC, angle CAB = angle DAC$
откуда вытекают равенства
$triangle ABD = triangle BAC, triangle CBD = triangle DAC$
и подобие всех граней тетраэдра.