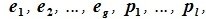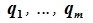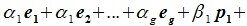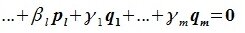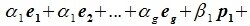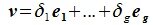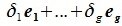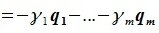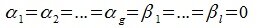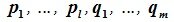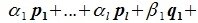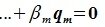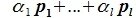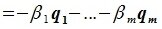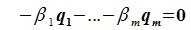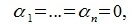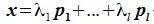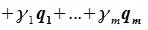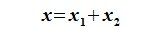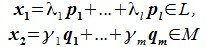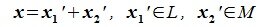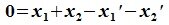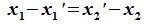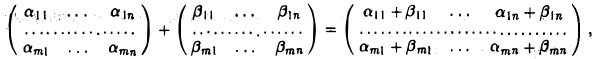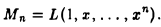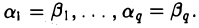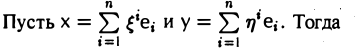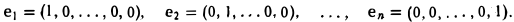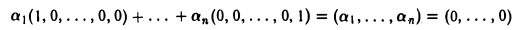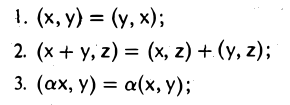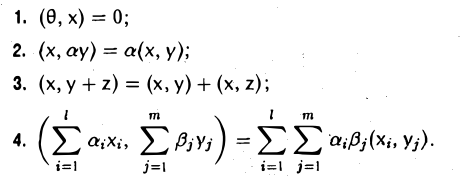Как найти подпространства линейного пространства - Исправление недочетов и поиск решений вместе с Examum.ru

9.1 Понятие линейного пространства

Рассмотрим множество V элементов x, y, z, … и множество R

действительных чисел. Определим операцию «сложения» элементов множества V (ее называют внутренней операцией): любой упорядоченной паре элементов

x V , y V	поставим в соответствие третий элемент	z V ,	называемый	их
«суммой», будем писать в этом случае z = x + y .
Введем также операцию «умножения» элементов множества V	на
действительное	число (эту операцию называют внешней); каждому	элементу
x V и действительному	числу α R поставим в	соответствие	элемент
z =αx = xα ,	где	z V . Потребуем, чтобы	операция	«сложения» элементов
множества	V	и операция	«умножения»	элементов	этого	множества	на

действительное число удовлетворяли следующим аксиомам:

I	Сложение коммутативно, т.е. x + y = y + x для любых x V , y V .
II	Сложение ассоциативно, т.е. (x + y)+ z = x + ( y + z) для любых x V ,

y V , z V .

III Существует нулевой элемент, т.е. такой элемент, который в сумме с любым элементом x дает тот же элемент x ; обозначим нулевой элемент символом θ , тогда x +θ = x , для любого x V .

IV Для каждого элемента x V существует противоположный элемент, т.е. такой элемент, который в сумме с данным дает нулевой элемент; элемент,

противоположный элементу x , обозначим	через − x ,	тогда x + (−x) =θ для
любого x V .			т.е. 1 x = x для любого
V Умножение на число 1 не меняет элемента,
x V .
Для любых x,	y V , α, β R :
VI	α(βx)= (αβ )x .
VII	α(x + y)=αx +αy .
VIII (α + β)x =αx + βx .
Множество V	элементов x, y, z, …,	в котором	определены операции

«сложения» элементов и «умножения» элемента на действительное число, удовлетворяющие аксиомам I – VIII, называется действительным линейным пространством (или действительным векторным пространством). Элементы действительного линейного пространства называют векторами.

Обращаем внимание читателя, что внутренняя операция «сложения» на самом деле может и не быть сложением в обычном понимании, а может быть, например, вычитанием, умножением, логарифмированием по определенному основанию и т.д. В точности также дело обстоит и с внешней операцией – «умножением». В дальнейшем, помня это, кавычки для удобства записи будем

222

опускать, однако обязательно будем оговаривать в каждом отдельном случае, что означает в этом конкретном примере операция сложения и что означает операция умножения.

Итак, дано определение действительного линейного пространства. Если бы мы предположили, что в множестве V определено умножение не только на действительные, но и на любые комплексные числа, то, сохраняя те же аксиомы I

– VIII, получили бы определение комплексного линейного пространства. Для определенности ниже рассматриваются действительные линейные пространства, однако все, что будет сказано в настоящей главе, переносится дословно на случай комплексных линейных пространств.

Для линейного пространства справедливы следующие теоремы:

Теорема 9.1 В линейном пространстве имеется единственный нулевой элемент.

Доказательство. Предположим, что в линейном пространстве V имеются два нулевых элемента θ1 и θ2 , тогда θ1 +θ2 =θ1 и θ1 +θ2 =θ2 , поэтому θ1 =θ2 .

Теорема 9.2 Для любого элемента x линейного пространства существует

единственный противоположный элемент − x .	x
Доказательство. Предположим, что для элемента	существует два
противоположных	элемента x1 и x2 , т.е. x + x1 =θ	и	x + x2 =θ , тогда
x1 = (x2 + x) + x1 = x2	+ (x + x1 ) = x2 , следовательно, x1 = x2 .

Теорема 9.3 Для элемента − x противоположным будет элемент x .

Доказательство. Поскольку − x + x = x + (−x) (по аксиоме I) и x +( −x ) =θ

(по аксиоме III), то − x + x =θ , а это означает, что x — элемент, противоположный элементу − x .

Теорема 9.4 Для любого элемента	x	произведение 0x =θ , где 0 – число
нуль, θ – нулевой элемент.			0x = 0x + (x + (−x)) = (0x + x) + (−x) =
Доказательство.	Так	как
= x( 0 +1) +( −x ) = x +( −x ) = θ. Итак, получим 0x = θ.
Теорема 9.5 Для любого элемента	x	произведение −1 x = −x , где (− x) —

элемент, противоположный элементу x .

Доказательство. Поскольку −1 x + x = (−1 +1)x = 0x =θ , или −1 x + x =θ , то −1 x — элемент, противоположный элементу x , т.е. (−1)x = −x .

Теорема 9.6 Для любого числа α произведение αθ =θ , где θ – нулевой элемент.

Доказательство.αθ =α(x + (−x)) =α(x + (−1)x) =αx +α(−1)x =αx + + (−αx)=θ , αθ =θ .

223

		Теорема 9.7 Если αx = 0 и α ≠ 0 , то x =θ .	1
		Доказательство. Пусть αx = 0 и α ≠ 0 , тогда	αx = 0 , или x =θ .

							α
		Теорема 9.8 Если αx = 0 и x ≠θ , то α = 0.
		Доказательство.		Предположим противное, т.е.	α ≠ 0 , получим
	1	(αx)=	1	0 = 0 , или	1	αx = x = 0 , то, что противоречит условию.
α	α	α
		Следствие. Равенство αx = 0 выполняется	тогда и	только тогда, когда
α = 0 или x =θ .

Следствие непосредственно вытекает из 4, 6 – 8.

Примеры линейных пространств:

1) Множество всех свободных векторов a(a1 , a2 , a3 ), где a1 , a2 , a3 могут

принимать любые действительные значения, для которых определены сложение и умножение вектора на число является линейным пространством. Обозначим это линейное пространство символом V3 . Отметим, что роль нулевого элемента здесь

играет нуль-вектор; для любого вектора a противоположным является − a .

2)Множество всех матриц размеров m × n , для которых определены сложение матриц и умножение матрицы на число обычным образом, является

линейным пространством. Роль нулевого элемента здесь играет нулевая матрица; для матрицы (aik )mn противоположной будет матрица (− aik )mn .

3)Множество {Pn (x)} всех алгебраических многочленов степени, не

превышающей натурального числа n , для которых операции сложения многочленов и умножения многочлена на действительное число определены обычными правилами, является линейным пространством. Роль нулевого элемента играет многочлен, все коэффициенты которого равны нулю; для многочлена

Pn (x) = a0 xn + a1 xn−1 +… + an−1 x + an .

противоположным будет

− Pn (x) = −a0 xn − a1 xn−1 −… − an−1 x − an .

4)	Множество	An , элементами	которого	являются	упорядоченные
совокупности n действительных	чисел	x = (x1, x2 , …, xn ),	y = (y1 , y2 , …, yn );
линейные операции над элементами An определяются формулами
x + y = ((x1 + y1 ), (x2 + y2 ),	…, (xn + yn )),
αx = (αx1 , αx2 , …, αxn );				− x = (− x1 , −x2 , …, − xn ) —
элемент	θ = (0, 0,…,0)	является	нулевым, элемент
противоположным элементу x = (x1 ,	x2 , …, xn ), является линейным пространством.

224

9.2 Линейная зависимость векторов

Вектор y называют пропорциональным вектору x , если y = kx для

некоторого числа k . В аналитической геометрии такие векторы называются

коллинеарными. Вектор y называют линейной комбинацией (конечной)

системы векторов x1 , x2 , …, xs , если существуют такие числа α1 , α2 , …, αs , что

y =α1x1 +α2 x2 + … +αs xs .

(9.1)

При этом говорят также, что вектор y линейно выражается через векторы

x1 , x2 , …, xs .

Если вектор b линейно выражается через систему вектора x1 , x2 , …, xs ,

то он будет линейно выражаться и через любую конечную систему векторов, включающую в себя систему x1 , x2 , …, xs .

Действительно, если выполняется равенство y =α1x1 +α2 x2 + … +αs xs + 0 xs +1 + … + 0 xr .

Это равенство означает, что вектор b линейно выражается через систему векторов x1 , x2 , …, xr .

Конечная система векторов x1 , x2 , …, xr называется линейно зависимой, если существуют такие числа α1 , α2 , …, αr , не все равные нулю, что

α1x1 +α2 x2 + … +αr xr = 0 .

(9.2)

В противном случае система векторов x1 , x2 , …, xr линейно независима.

Система векторов x1 , x2 , …, xs линейно зависима тогда и только тогда,

когда хотя бы один из ее векторов линейно выражается через остальные векторы.

Действительно, если система векторов x1 , x2 , …, xs линейно зависима, то выполняется равенство

α1x1 +α2 x2 + … +αs xs = 0 ,			(9.3)
в котором, например αs ≠ 0 . Тогда из этого равенства получаем:
x	s	= −α1 x − α2 a		− … − αs −1 x	s −1	.
	αs 1	αs		2	αs
Это означает, что вектор xs	линейно выражается через систему векторов
x1 , x2 , …, xs −1 .					линейно выражается через систему векторов
Наоборот, пусть вектор xs
x1 , x2 , …, xs −1 , т.е.
xs	=α1x1 +α2 x2 + … +αs −1xs −1 .
Тогда верно	и	равенство (9.3), в котором αs = −1 ≠ 0 . Значит, система

векторов x1 , x2 , …, xs линейно зависима.

Например, рассмотрим линейное пространство многочленов не выше

второй степени. Докажем, что векторы	p =1 + 2t + 3t 2	,	p	2	= 2 + 3t + 4t 2	и
	1

p3 = 3 + 5t + 7t 2 линейно зависимы.

225

Действительно, эти вектора линейно зависимы, так как p3 =1 p1 +1 p2 .

Совокупность элементов, каждый их которых есть элемент системы x1 , x2 , …, xn , называется подсистемой этой системы.

Две конечные системы векторов называют эквивалентными, если они линейно выражаются одна через другую.

Непосредственно легко проверить, что

1)эквивалентность систем векторов обладает свойством транзитивности, т.е. если первая система векторов эквивалентна второй, а вторая – третьей, то первая система векторов эквивалентна третьей;

2)если вектор линейно выражается через данную систему векторов, то он линейно выражается через любую другую систему векторов, эквивалентную данной.

Теорема 9.9 (основная теорема о линейной зависимости векторов)

Пусть даны две системы векторов x1 , x2 , …, xr и y1 , y2 , …, ys , причем первая

линейно независима и линейно выражается через вторую. Тогда число векторов в первой системе не превышает числа векторов во второй, т.е. r ≤ s .

Доказательство. Утверждение теоремы, по существу, означает, что из s векторов нельзя создать систему линейных комбинаций этих векторов, которая, с одной стороны, линейно независима, а с другой – содержит более s векторов.

По условию теоремы система векторов x1 , x2 , …, xr линейно независима и

линейно

выражается

через векторы системы y1 , y2 , …, ys . Следовательно,

существуют такие числа αij , что выполняются неравенства

=α

+α

+ … +α

x2 =α21 y1 +α22 y2 + … +α2s ys

(9.4)

…………………………………

=α

+α

r 2

+ … +α

Допустим, что r > s , и рассмотрим линейную комбинацию векторов

λ1x1 + λ2 x2 + … + λr xr .

В силу равенств (9.4) эту линейную комбинацию можно представить следующим образом:

λ1x1 + λ2 x2 + … + λr xr = ∑i =r1λi xi = ∑i =r1λi ∑j s=1xi y j = ∑j s=1 ∑i =r1 xij λi y j .

В рассматриваемой линейной комбинации векторов попытаемся подобрать числа λ1 , λ2 , …, λr так, что они одновременно не равны нулю, но при этом все

коэффициенты при векторах y1 , y2 , …, ys обнуляются. Это означает, что набор чисел λ1 , λ2 , …, λr является решением системы линейных однородных уравнений

226

α λ

+α

+ … +α

= 0,

11 1

21λ1 +α22λ2 + … +α2r λr = 0,

…………………………………

α λ

+α

r 2

+ … +α

= 0.

r1 1

При r > s число неизвестных в системе превышает число уравнений, поэтому она имеет ненулевое решение. Любое ненулевое решение системы дает такой набор коэффициентов λ1 , λ2 , …, λr , одновременно не обращающихся в нуль,

для которых

λ1x1 + λ2 x2 + … + λr xr = 0 .

Существование таких коэффициентов равносильно линейной зависимости векторов x1 , x2 , …, xr , что противоречит условию теоремы. Значит,

предположение r > s неверно и на самом деле r ≤ s . Что и требовалось доказать.

Следствие. Любые две эквивалентные линейно независимые системы векторов имеют одинаковое число векторов.

Действительно, по доказанной теореме для двух линейно независимых эквивалентных систем векторов количество векторов в первой системе не превышает количества векторов во второй. Но системы в этом утверждении можно поменять местами, поэтому в первой системе не меньше векторов, чем во второй.

Заметим, что любые две максимальные линейно независимые подсистемы данной системы векторов эквивалентны. Значит, согласно доказанному следствию они имеют одно и то же число векторов.

9.3 Размерность и базис линейного пространства

Линейное пространство V называется n —мерным, если в нем существует n линейно независимых векторов, а любые n +1 векторы являются линейно зависимыми. Число n называется в этом случае размерностью линейного пространства V . Итак, число n называется размерностью линейного пространства V , если выполняются следующие условия:

1)в V существует n линейно независимых векторов;

2)любая система n +1 векторов из V линейно зависима.

Размерность линейного пространства V обозначается dimV (от французского слова dimension – размерность). Если пространство состоит из одного нулевого элемента, его размерность считают равной нулю. Введенное понятие размерности согласуется с наглядным представлением о ней; так, пространство V3 всех свободных векторов является трехмерным ( dimV3 = 3 ),

пространство V2 — двумерным, пространство V1 — одномерным.

Базисом n -мерного линейного пространства Vn называется любая упорядоченная система n линейно независимых векторов этого пространства.

227

Линейное пространство, в котором имеется базис, состоящий из конечного числа векторов, называется конечномерным. Примерами конечномерных пространств являются пространства V1 , V2 , V3 , An , рассмотренные выше.

Линейное пространство называется бесконечномерным, если при любом натуральном числе m в нем найдется m линейно независимых векторов.

Примером бесконечномерного пространства будет множество всевозможных действительных функций действительного переменного, если сложение функций и их умножение на действительное число понимать так, как это принято в теории функций, т.е. как сложение или умножение на число значений функций при каждом значении независимого переменного.

Приведем примеры базисов некоторых линейных пространств.

1)Базис пространства V3 образует любая тройка некомпланарных

векторов, так как эти векторы линейно независимы.

2)Базис пространства V2 образуют два любых неколлинеарных вектора,

поскольку они линейно независимы и любой вектор плоскости, определяемый этими двумя векторами, можно разложить по ним.

3) Базисом линейного пространства V1 является любой ненулевой вектор, коллинеарный данной прямой.

4)	Многочлены p	0	(x)=1,	p (x) = x ,	p	2	(x) = x2	образуют базис в
			1

пространстве P2 . Действительно, эти многочлены линейно независимы, и любой

многочлен	p(x) = a + bx + cx2 из P	можно представить в виде линейной
	2	p2 (x).
комбинации многочленов p0 (x), p1(x),

5)Рассмотрим некоторое линейное пространство An , состоящее из

векторов xi = (xi	, xi , …,	xi ), i =	. Докажем,	что система	векторов этого
1, n
1	2	n
пространства
e1 = (1, 0, …, 0), e2 = (0, 1, 0, …, 0) , …, en = (0, 0, …, 0, 1)	(9.5)
— линейно независима, а совокупность e1 , e2 , …, en ,	x , где x = (x1 ,	x2 , …, xn ) — любой

элемент этого пространства, образует линейно зависимую систему, т.е. докажем, что векторы e1 , e2 , …, en образуют базис пространства An . Действительно,

линейная комбинация векторов (9.5) представляет вектор

α1e1 +α2e2 + … +αn en = (α1 , α2 , …, αn ),

который является нулевым лишь при α1 =α2 =… =αn = 0 . Это означает, что

векторы (9.5) линейно независимы. Поскольку

x = (x1 , x2 , …, xn )= x1e1 + x2e2 + … + xn en

есть линейная комбинация векторов (9.5), то система e1 , e2 , …, en , x линейно зависима. Следовательно, линейное пространство An будет n -мерным, а система векторов (9.5) образует базис этого линейного пространства.

228

Очевидно	следующее	утверждение. Если dim R = n ≥1, то в
пространствеR существует базис из n	элементов. В качестве базиса можно
взять любые n линейно независимых элементов.
Теорема	9.10 Пусть	линейное	пространство Vn обладает базисом
e1 , e2 , …, en . Тогда любой вектор x из Vn	единственным образом представляется
в виде
x = x1e1 + x2e2 + … + xn en .		(9.6)

Доказательство. В силу определения базиса линейного пространства V любой вектор x V имеет хотя бы одно представление вида (9.6). Предположим, что наряду с разложением (9.6) есть и другое разложение

x = x1′e1 + x2′e2 + … + x′n en

вектора x . Тогда будет выполняться равенство

x = x1e1 + x2e2 + … + xn en = x1′e1 + x′2e2 + … + xn′en ,

которое приводит к равенству

(x1 − x1′)e1 + (x2 − x′2 )e2 + … + (xn − x′n )en = 0 .

Последнее равенство в силу линейной независимости системы векторов

e1 , e2 , …, en	возможно лишь в том случае, когда
	′	′		′	,
(x1 − x1 )= 0,	(x2 − x2 )= 0,	…, (xn − xn )= 0
т.е. при x1	′	′	′	. Это доказывает, что разложение вектора по
= x1 , x2	= x2 , …,	xn = xn

базису единственно.

Линейное выражение (9.6) вектора x через векторы базиса, единственное в силу сформулированной теоремы, называют разложением вектора x по базису e1 , e2 , …, en . Это разложение удобно записывать в матричной форме

x = x1e1 + x2e2 +… + xnen = (e1 , e2 , …, en ) xM2 = e [x],

где e = (e1 , e2 , …, en ) — заданный базис, записанный в виде матрицы-строки, а [x] —

столбец коэффициентов	разложения вектора	x	по базису,	называемых
координатами вектора x в базисе e .
Например, пусть	V	-пятимерное линейное	пространство	с базисом
e1 , e2 , e3 , e4 , e5 , найдем координаты векторов e2	и	x = 3e1 − e3 + 2e4	в данном
базисе.
Решение. Вектор x представим в виде
x = 3e1 + 0e2 + (−1)e3 + 2e4 + 0e5 ,
следовательно, (3, 0, −1, 2, 0)	— координаты вектора x в базисе e1 , e2 , e3 , e4 , e5 .
Аналогично e2	= 0e1 +1e2 + 0e3 + 0e4 + 0e5 ,	следовательно, e2 (0, 1, 0, 0, 0) —
координаты вектора e2	в заданном базисе.

229

Векторы линейного пространства V полностью определяются своими координатами в данном базисе. При этом операции над векторами сводятся к аналогичным операциям над их координатами. Так, для векторов

x = x1e1 + x2e2	+ … + xn en и y = y1e1 + y2e2	+ … + yn en
условие их равенства, x = y , равносильно условиям
x1 = y1 ,	x2 = y2 , …,	xn = yn ,
а равенства
x + y = (x1e1 + x2e2 + … + xn en )+ (y1e1 + y2e2 + … + yn en )=
= (x1 + y1 )e1 + (x2 + y2 )e2 + … + (xn	+ yn )en	(9.7)

λx = λ(x1e1 + x2e2 + … + xn en )= (λx1 )e1 + (λx2 )e2 + … + (λxn )en

показывают, что при сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.

Например, в некотором базисе даны векторы x(2, −1, 3, 5) и y(−1,4, 0, − 2) . Найдем координаты вектора 2x − 3y .

Решение. Учитывая свойство (9.7), находим координаты вектора 2x − 3y : (2 2 − 3 (−1), 2 (−1) − 3 4, 2 3 − 3 0, 2 5 − 3 (−2)) = (7, −14, 6, 16).

9.4 Ранг системы векторов линейного пространства
Рассмотрим систему m векторов
x1 = (x11 , x21 , …, xn1 ),
x2 = (x12 , x22 , …, xn2 ),		(9.8)
………………………..
		= (x				)
x	m	, x	2m	, …, x	nm
	1m

линейного n -мерного пространства, координаты которых заданы в одном и том же базисе. Системе векторов (9.8) поставим в соответствие матрицу

x	x	…	x
11	12		1m
x21	x22	…	x2m	,	(9.9)
X =	…	…	…
…
	xn2	…
xn1	xnn

в k -м столбце которой записаны координаты вектора xk ( k =1, 2, …, m ). Матрицу

(9.9) называют матрицей системы векторов (9.8) в данном базисе, а ранг этой матрицы – рангом системы векторов x1 , x2 , …, xm . Обратно, если дана матрица

(9.9), ей можно поставить в соответствие систему (9.8) m векторов линейного n — мерного пространства. Столбцы матрицы (9.9) линейно зависимы, если векторы (9.8) линейно зависимы и обратно.

Приведем без доказательства теорему, которая позволяет судить о линейной независимости векторов, заданных своими координатами.

230

Теорема 9.11 Для того чтобы m векторов линейного пространства были линейно независимы, необходимо и достаточно, чтобы ранг матрицы этой системы был равен m .

Следствие 1. Система n векторов n -мерного линейного пространства линейно независима тогда и только тогда, когда матрица этой системы векторов является невырожденной.

Следствие 2. Если ранг матрицы системы m векторов линейного пространства равен r , максимальное число линейно независимых векторов этой системы равно r .

Например, найдем максимальное число линейно независимых векторов в системе a1 (1, 4, 2, 7) , a2 (−1, − 2, − 3, − 6) , a3 (0, 5, 0, 5) , a4 (3, 0, 6, 9) , a5 (2, 3, 1, 6) .

Решение. Матрица данной системы векторов имеет вид

	1	−1	0	3	2
	4	− 2	5	0	3

A =	2	− 3	0	6	1	.

	7	− 6	5	9	6

Так как ранг этой матрицы равен трем, то максимальное число линейно независимых векторов этой системы равно трем.

Замечание. Можно доказать, что максимальное число линейно независимых строк всякой матрицы равно максимальному числу ее линейно независимых столбцов, т.е. равно рангу этой матрицы.

9.5 Матрица перехода от базиса к базису. Преобразование координат вектора

Рассмотрим в линейном пространстве V два базиса:

e1, e2 , …, en ;				(9.10)
e1′, e2′ , …, en′ .				(9.11)
Матрицей перехода от базиса (9.10) к базису (9.11) называется матрица
системы векторов e1′, e2′ , …, en′	в базисе e1, e2 , …, en .
Из определения следует, что если
t	t	…	t
11	12		1n
t21	t22	…	t2n	(9.12)
T =		…	…
… …
	tn2	…
tn1	tnn

есть матрица перехода от базиса (9.10) к базису (9.11), то

231

	e′	= t e	+ t e	+… + t	e	n	;
	1	11 1	21 2		n1
	e2′	= t12e1 + t22e2 +… + tn2en ;

	………………………………..


или	en′ = t1ne1 + t2ne2 +… + tnnen
′	′	′	e2 … en ) T .	(9.13)

	(e1	e2 … en )= (e1

Из теоремы о линейной независимости векторов следует, что матрица перехода от базиса к базису является невырожденной и всякую невырожденную матрицу порядка n можно рассматривать как матрицу перехода от базиса к базису в n -мерном пространстве.

Очевидно, что матрица T −1 ,	обратная матрице (9.12),	является матрицей
перехода от базиса (9.11) к базису (9.10).		базис i, j ,
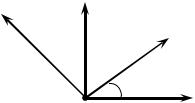
Например, рассмотрим в линейном пространстве	M 2	а также
базис e1, e2 (рисунок 103).	j
		e2
			е1
			φ
			i
			Рисунок 103
В этом случае
e = i cosϕ + j sinϕ;
1
e2 = −isinϕ + j cosϕ.
Следовательно, матрицей перехода от базиса i, j	к базису e1, e2	является
матрица
cosϕ	− sinϕ
		,
	cosϕ
sinϕ
тогда как матрицей перехода от базиса e1, e2 к базису i, j	является матрица
	cosϕ	sinϕ
A−1 =		.
	− sinϕ
	cosϕ

Задача преобразования координат заключается в нахождении зависимости между координатами вектора в разных базисах.

Формулы, связывающие координаты вектора в разных базисах,

называются формулами преобразования координат.

Теорема 9.12 Если x1, x2 , …, xn — координаты вектора x в базисе

e1, e2 , …, en , а x1′, x2′ , …, xn′ — координаты этого же вектора в базисе e1′, e2′ , …, en′ , то имеет место следующее соотношение:

232

x		x′
	1			1
x2		x2′		(9.14)
	M	=T		M



xn		xn′
или
X =TX ′,
где X = (x1 x2	… xn )T ; X ′ = (x1′ x2′ … xn′ )T ; T — матрица перехода	от базиса
e1, e2 , …, en к базису e1′, e2′ , …, en′ .
Доказательство. Из условия теоремы следует, что
x =	(e1 e2	… en )X ;	(9.15)
x = (e1′ e2′	… en′ )X ′.	(9.15)’
Учитывая соотношение (9.13), из равенства (9.15)’ получаем
x =	(e1 e2 … en )TX ′.	(9.16)

Так как равенства (9.15) и (9.16) есть символическая запись разложения вектора x по базису e1, e2 , …, en , а для каждого вектора разложение единственно,

то
X =TX ′.								(9.17)
Из соотношение (9.17) выразим матрицу X ′, имеем
TX ′ = X ,
T −1TX ′ =T −1 X .
Таким образом матрица X ′	запишется в виде
X ′ =T −1 X .							(9.18)
Формулы (9.17) и (9.18) являются формулами преобразования координат.
Например,	пусть вектор x в базисе e1, e2	имеет координаты (1, − 2).
Найдем координаты этого вектора в базисе e1′ = e1,	e2′	= e1 + e2 .
Решение. Матрица перехода от базиса e1, e2	к базису e1′, e2′ имеет вид
T =		1	1
		.
		0
		1
Искомые координаты x1′, x2′ находим по формуле (9.18):
x′		=T −1		1
1				.
					− 2
x2′
Матрица, обратная матрице T , имеет вид:
T −1			1	−1
=			.
			0
				1
Таким образом,
x′		=	1 −1	1		3
1						=	.

x2′			0		1	− 2		− 2
Следовательно,	x1′ = 3,	x2′ = −2 .

233

9.6 Изоморфизм линейных пространств

Пусть даны два линейных пространства V и U . Если между элементами x V и y U этих пространств установлено взаимно-однозначное соответствие,

будем писать x ↔ y .

Два линейных пространства V и U называются изоморфными, когда между их элементами можно установить взаимно однозначное соответствие такое, что если x1 ↔ y1 , x2 ↔ y2 , где x1 , x2 V , y1 , y2 U , то

1) (x1 + x2 )↔ (y1 + y2 );

2) αx1 ↔αy1 ,

где α — действительное число.

Обозначение: V ~ U — линейное пространство V изоморфно линейному пространству U .

Если V ~ U и x ↔ y , где x V , а y U , то y называют образом элемента

x , а x называют прообразом элемента y .
Отметим,	что если V ~ U , то θ →θ′, где θ	и θ′ —	нулевые элементы
пространств V	и U . Примем без доказательства	теорему	о необходимом и

достаточном условии изоморфизма двух линейных пространств.

Теорема 9.13 Два линейных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность.

Все линейные пространства одной и той же размерности изоморфны между собой.

Таким образом, различные линейные пространства одной и той же размерности с алгебраической точки зрения тождественны.

Очевидно, очень важной является следующая теорема.

Теорема 9.14 Если линейные пространства R и R′ изоморфны, то

линейно независимым элементам

x1 , …,

пространства

R соответствуют

линейно независимые элементы

′

x1 , …, xm пространства

линейно

Доказательство.

Предположим,

что элементы

x1 , …, xm

независимы, а их образы

′

линейно зависимы. Тогда существует линейная

x1 , …,

комбинация

элементов

′

, равная нулевому элементу θ

′

, не все

x1 , …, xm

коэффициенты которой равны нулю. В силу изоморфизма пространств R и R′ эта

линейная

комбинация

является

образом

линейной

комбинации

элементов

x1 , …, xm

с теми же коэффициентами.

С другой стороны, элемент θ′

является

образом

нулевого элемента

пространства R . Следовательно, указанная

линейная комбинация элементов x1 , …,

xm , не все коэффициенты которой равны

нулю, равна

нулевому

элементу

θ ,

поэтому элементы

x1 , …, xm

линейно

зависимы, что противоречит условию. Полученное противоречие доказывает, что элементы x1′, …, x′m также линейно независимы.

234

Приведем примеры изоморфных линейных пространств:

1) Линейное пространство X геометрических векторов, выходящих из начала координат трехмерного пространства, с обычными операциями сложения векторов и умножения вектора на число изоморфно действительному арифметическому пространству K3 , так как каждому вектору x X можно

поставить во взаимно однозначное соответствие вектор-столбец x′ = (x1 , x2 , x3 )T

его координат в некотором фиксированном базисе. При таком соответствии будут выполняться соотношения

x + y ↔ x′ + y′ = (x1 + y1 , x2 + y2 , x3 + y3 )T ;

λx ↔ λx′ = (λx1 , λx2 , λx3 )T .

2)Линейное пространство M 22 квадратных матриц второго порядка над

полем P с обычными операциями сложения матриц и умножения матрицы на элементы поля P и арифметическое пространство K4 над полем P изоморфны,

так как каждой матрице

a	a
A = 11	12

a21	a22

из M 22 во взаимно однозначное	соответствие можно поставить вектор-столбец
α = (a11 , a12 , a21 , a22 )T из K4 и при	этом будут выполняться соотношения

A + B ↔α + β ,	λA ↔ λα .
3) Линейное	пространство P2 (x) многочленов степени n ≤ 2 с

действительными коэффициентами и с обычными операциями сложения

многочленов и умножения многочлена на	действительное число изоморфно
действительному		арифметическому пространству K3 , так	как многочлену
f (x) = a	0	+ a x + a	2	x2	можно поставить	в соответствие	вектор-столбец
	1

(a0 , a1 , a2 )T , при этом будут выполняться соотношения

(a0 + a1 x + a2 x2 )+ (b0 + b1 x + b2 x2 )↔ (a0 , a1 , a2 )T + (b0 , b1 , b2 )T , λ(a0 + a1 x + a2 x2 )↔ λ(a0 , a1 , a2 )T .

9.7 Подпространство линейного пространства

Введем понятие подпространства. Множество W V называется

подпространством линейного пространства V , если выполняются следующие условия:

1)во множестве W определены те же операции, что и в множестве V ;

2)если x, y W , то x + y W ;

3)если x W , то αx W .

Очевидно, всякое подпространство W линейного пространства V является линейным пространством, т.е. в W выполняются аксиомы I – VIII.

235

Прежде всего, в W имеется нулевой элемент θ : если x W , то 0x =θ W . Для любого элемента x W имеется противоположный элемент − x : если x W , то (−1)x = −x W . Легко видеть, что аксиомы I – VIII для элементов множества

W будут выполнены. Отметим, что нулевой элемент θ линейного пространства V образует подпространство данного пространства, которое называют нулевым подпространством. Само линейное пространство V можно рассматривать как подпространство этого пространства. Эти подпространства называют тривиальными, а все другие, если они имеются, — нетривиальными.

Приведем примеры нетривиальных подпространств линейных пространств.

1)Множество V2 всех свободных векторов a(a1 , a2 ), параллельных

некоторой плоскости, для которых обычным образом определены операции сложения векторов и умножения вектора на число, является подпространством линейного пространства V3 .

2)Множество V1 всех свободных векторов a(a1 ), параллельных некоторой прямой, представляет подпространство линейного пространства V2 .

3)Множество {Pn−1 (x)} всех алгебраических многочленов степени, не

превышающей натурального числа n −1, является подпространством линейного пространства {Pn (x)}.

9.8 Линейная оболочка системы векторов

Пусть в линейном пространстве V над полем Р дана система векторов a1, a2 , …, ak . Множество всевозможных линейных комбинаций

α1a1 +α2a2 + … +αk ak

этой системы называют линейной оболочкой системы векторов a1, a2 , …, ak .

Теорема 9.15 Линейная оболочка L системы векторов a1, a2 , …, ak

является подпространством в X .

Доказательство. Действительно, если векторы a и b принадлежат L , т.е. имеют представления

a =α1a1 +α2a2 + … +αk ak , b = β1a1 + β2a2 + … + βk ak ,

то и векторы a + b и λa имеют такие представления: a + b = (α1 + β1 )a1 + (α2 + β2 )a2 + … + (αk + βk )ak , λa = (λα1 )a1 + (λα2 )a2 + … + (λαk )ak .

Следовательно, они принадлежат L, что и требовалось доказать. Линейную оболочку L системы векторов a1, a2 , …, ak также называют

подпространством, порожденным этой системой векторов, или подпространством, натянутым на эту систему векторов, и обозначают

L = (a1, a2 , …, an ).

236

Теорема 9.16 Линейное подпространство конечномерного линейного пространства является конечномерным, и размерность подпространства не превышает размерности всего линейного пространства.

Доказательство. Действительно, размерность конечномерного линейного пространства V может быть определена как максимальное количество линейно независимых векторов в этом пространстве. Очевидно, что максимальное количество линейно независимых векторов в любом подмножестве L в V не превышает максимального количества линейно независимых векторов в V . Отсюда следует утверждение теоремы.

Любое конечномерное линейное пространство порождается конечной системой векторов, например, любым своим базисом. Согласно доказанной теореме это верно и для всякого линейного подпространства линейного пространства.

Теорема 9.17 Пусть L — подпространство п-мерного линейного пространства V . Любой базис a1, a2 , …, ak в L можно дополнить до базиса

a1, a2 , …, ak , ak +1,…, an всего линейного пространства V , причем линейному

подпространству L принадлежат те и только те векторы, которые в указанном базисе имеют столбцы координат вида

(x1′, x2′ , …, xk′ , 0, …, 0)T .

(9.19)

Доказательство. Действительно, любой базис в L, как и вообще любую линейно независимую систему векторов в V можно дополнить до базиса линейного пространства V . Если вектор х имеет столбец координат (9.19), то он имеет представление

x = x1′a1 + x2′a2 + … + xk′ ak + 0 ak +1 + … + 0 an = x1′a1 + x2′a2 + … + xk′ ak

и, следовательно, принадлежит L как линейная комбинация векторов, принадлежащих L. Если вектор х принадлежит L, он может быть разложен по базису a1, a2 , …, ak

x = x1′a1 + x2′a2 + … + xk′ ak

Это разложение в то же время является разложением вектора x в базисе a1, a2 , …, an линейного пространства V , дающим столбец координат вида (9.19).

Теорема 9.18 Пусть V – конечномерное линейное пространство и в нем задан базис. Тогда для любого линейного подпространства L в V можно указать такую однородную систему линейных уравнений Ах = 0, что множество координатных столбцов всех векторов L будет совпадать с множеством решений системы Ах = 0.

Доказательство. Пусть e1, e2 , …, en – заданный базис в V . Выберем в L некоторый базис в a1, a2 , …, ak и дополним его векторами ak +1, ak +2 , …, an до

базиса в V . Из предыдущей теоремы вытекает, что множество векторов линейного подпространства L в базисе a1, a2 , …, an описывается системой

уравнений xk′ +1 =… = xn′ = 0 .

237

Пусть T – матрица перехода от базиса e1, e2 , …, en к базису a1, a2 , …, an . Тогда столбец координат xe вектора в базисе a1, a2 , …, an связан со столбцом координат xe′ этого же вектора в базисе e1, e2 , …, en равенством xe =Txa . Если столбец координат ха является решением однородной системы Ах = 0, то в силу соотношения xa =T −1xe столбец координат xe , является решением однородной системы AT −1x = 0 . Верно и обратное: если хе есть решение системыAT −1x = 0 , т.е. AT −1xe = 0 , то Axa = 0 , т.е., столбец ха является решением системы Ax = 0 . Из

этих рассуждений вытекает следующее: если некоторое множество в заданном базисе описывается однородной системой линейных уравнений (иными словами, совокупность всех столбцов координат векторов множества совпадает с множеством решений системы), то и в любом другом базисе это множество описывается некоторой системой линейных уравнений.

Так как линейное подпространство L в базисе a1, a2 , …, an описывается

однородной системой линейных уравнений, то это подпространство в соответствии с только что доказанным и в базисе e1, e2 , …, en описывается

системой линейных уравнений.

Однородную систему линейных уравнений, описывающую данное линейное подпространство L, называют общими уравнениями этого подпространства.

Например, составим общие уравнения линейного подпространства L = a1, a2 в четырехмерном линейном пространстве V , если векторы a1 и a2

заданы своими координатами в некотором базисе e :

[a	]	= (1, 1, 2, 0)T ,	[a	2	]	= (1, −1, 0, 2)T .
1	e			e

Решение. Нетрудно убедиться в том, что система векторов a1 и a2 линейно

независима и потому составляет базис в линейном подпространстве L. Дополним эту систему до базиса в линейном пространстве V векторами a3 и a4 , в качестве

которых; можно взять пару векторов из базиса e :

[a3 ]e = (0, 0, 1, 0)T ,		[a4 ]e = (0, 0, 0, 1)T .
Матрицей	перехода	от базиса e к базису a = (a1 , a2 , a3 , a4 ) является
матрица			1	1	0	0

			1	−1	0	0
T =			,
	2	0	1	0

			0	2	0	1

обратной к которой является матрица
			1 2	1 2			0	0

T	−1		1 2	−1 2 0 0
	=	−1	−1		1	0	.

				−1	1			0	1

238

В базисе a линейное подпространство описывается однородной системой из двух уравнений x3′ = 0 , x4′ = 0 , которая в матричной форме имеет вид:

x′

0 0 1 0

x′

x3′

0 0 0 1

x4′

Применив

формулу

xa =T −1xe ,

полученную систему

преобразуем в

систему

1 2 1 2 0 0 x′

1 2 0 0

0 0 1 0 1 2

−

x2′

−1

−1 1 0

x3′

0 0 0 1

−1

1 0 1

x4′

после умножения матриц – в систему

−1 −1 1 0 x2

−1 1 0 1

или

− x − x

+ x

= 0

− x1 + x2 + x4 = 0,

описывающую линейное подпространство L в базисе e .

Общие

уравнения

линейного

подпространства

определяются

неоднозначно: достаточно систему линейных уравнений заменить любой эквивалентной системой, чтобы получить другие общие уравнения того же линейного подпространства. В рассмотренном примере ответ зависит от того, какими векторами a3 и a4 мы дополняем систему a1 , a2 до базиса.

Например, если положить

[a3 ]e = (0, 0, −1, −1)T , [a4 ]e = (0, 0, −1, 1)T ,

то, повторив все вычисления, получим уже другую систему линейных уравнений, описывающую заданное линейное подпространство L в базисе e , именно:

x1 − 12 x3 − 12 x4 = 0,

x2 − 1 x3 + 1 x4 = 0.

2 2

Если подпространство задано общими уравнениями, то для построения

базиса этого подпространства следует построить фундаментальную систему решений для общих уравнений подпространства.

239

Если a1, a2 , …, ak – базис линейного подпространства	L в линейном
пространстве V , то L можно задать уравнением
x = t1a1 + t2a2 + … + tnan ,	(9.20)

которое называют параметрическим уравнением подпространства L в векторной форме.

Пусть векторы a1, a2 , …, ak заданы своими координатами в некотором базисе пространства V :

Тогда векторное уравнение следующим образом:

= a t

+ a t

+… + a

11 1

x2 = a21t1 + a22t2 +… + a2k tk ,

…………………………………

= a

+ a

+… + a

n1 1

a1k ak = aM2k .

ank

(9.20) в координатах можно записать

(9.21)

Систему (9.21) называют параметрическими уравнениями подпространства L в координатной форме.

Если из параметрических уравнений (9.21) подпространства L исключить параметры t1, t2 , …, tk , получим общие уравнения подпространства L. Таким

образом, мы пришли еще к одному способу получения общих уравнений подпространства.

Например, подпространство L = a1, a2	, где
a = (1, 1, 2, 0)T ,	a	2	= (1, −1, 0, 2)T	,
1

зададим параметрическими уравнениями в векторной и координатной формах, а также общими уравнениями.

Решение: Векторное уравнение (9.20) в данном случае имеет вид:

		1			1
		1
x = t			+ t	−1	.
			2
1	2		0

		0			2

Переходя к координатам, получаем координатную форму, параметрических уравнений:

x1 = t1 + t2 ,x2 = t1 − t2 ,x3 = 2t1,

x4 = 2t2 .

240

Исключив параметры t1 и t2 , получим общие уравнения подпространства

2x1 − x3 − x4 = 0,2x2 − x3 + x4 = 0.

9.9 Пересечение подпространств. Сумма подпространств

Пусть в линейном пространстве V даны подпространства L1 и L2 . Множество L1 ∩ L2 векторов, принадлежащих как L1 , так и L2 , является подпространством в V . Его называют пересечением подпространств L1 и L2 .

Множество всех векторов х вида x = a + b , где a L1, b L2 , называют суммой подпространств L1 и L2 и обозначают через L1 + L2 . Если при этом пересечение L1 ∩ L2 – нулевое подпространство, то сумму L1 + L2 называют прямой суммой и обозначают через L1 L2 .

Теорема 9.19 Сумма подпространств является подпространством.

Доказательство. Пусть x = a + b , y = c + d , где a, c L1 , b, d L2 . Тогда

x + y = (a + c) + (b + d ) L1 + L2 ,

поскольку

a + c L1	и	b + d L2 .
Аналогично для любого числа α имеем:
αx =αa +αb L1 + L2 ,
так как	и	αb L2 .
αa L1

Таким образом, доказано, что сумма подпространств является подпространством.

Понятия пересечения и суммы подпространств распространяются на любое число подпространств.

Теорема 9.20 Если сумма подпространств L1 и L2 в V является прямой,

то представление любого	вектора	х в виде	x = a + b ,	где a L1,	b L2 ,
единственно.				каждый вектор x V
В частном случае, V = L1 L2	имеет представление
x = a + b , причем единственное. В	этом случае подпространства	L1	и L2
называют прямыми дополнениями друг друга,	а слагаемое a L1 —	проекцией
вектора х на подпространство L1 параллельно подпространству L2 .
Например, в пространстве K4 построим какое-либо прямое дополнение L2
к подпространству L1 = a1, a2 , где
a = (1, 1, 1, 0)T ,	a	2	= (1, 0, 1, 0)T ,
1
и найдем проекцию вектора	x = (2, 1,5, 5)T на L параллельно	L	2	.
				1

241

Решение. Векторы a1 и a2 линейно независимы и поэтому составляют базис в подпространстве L1 . Дополним систему векторов a1 , a2 до базиса во всем

пространстве V , например, векторами
b = (0, 0, 1, 0)T ,		b = (0, 0, 0, 1)T
1					2
и положим L2 = b1, b2	. Очевидно,	что L2 является искомым подпространством.
Далее запишем векторное равенство			0
							2
							1			0
x = (a	+ a	2	)+ (3b	+ 5b )=			+	,
1			1	2		2			3

							0			5

где (2, 1, 2, 0)T L ,		(0, 0, 3, 5)T	L .	Следовательно, проекцией	вектора
x = (2, 1,5, 5)T			1						2
на подпространство	L	параллельно подпространству L	2	является
вектор x = (2, 1, 2, 0)T .						1

1
Пусть L1 = a1, a2 , …, ak ,	L2 = b1, b2 , …, bl — подпространства в линейном
пространстве	X . Чтобы найти какой-либо базис в подпространстве	L1 + L2 ,

следует выделить какую-либо максимальную линейно независимую подсистему системы векторов

a1, a2 , …, ak , b1, b2 , …, bl .

Для этого достаточно составить матрицу из координатных столбцов этих векторов и в этой матрице выделить какой-либо базисный минор. Векторы, на координатных столбцах которых находится базисный минор, образуют базис в подпространстве L1 + L2 . Отметим, что базисный минор можно выбирать не в

исходной, а преобразованной матрице (после выполнения последовательности элементарных преобразований строк).

Например, найдем базис суммы L1 + L2	подпространств L1 = a1, a2 , a3 и
L2 = b1, b2 , b3 , если											= (1, −1, 1, −1)T ,
a = (1, 1, 1, 1)T	,			a	2	= (1, 1, −1, −1)T	,	a
1														3	= (3, −1, 1, 1)T .
b = (1, −1, −1, 1)T ,		b = (2, − 2, 0, 0)T ,	b
1									2					3
Решение. Составим матрицу
									1	1	1	1	2	3

(a	, a	2	, a	3	, b , b	, b	)=	1	1 −1	−1	− 2	−1 .
1			1	2	3				−1		−1
									1	1	0	1
											−1	−1	1	0	1
									1

Проводя элементарные преобразования строк матрицы, приведем ее к ступенчатому виду:

242

1	1	1	1	2	3
0	− 2	0	− 2	− 2	− 2

0	0	− 2	2	0	0	.

0	0	0	− 4	− 4	−4

Видим, что ранг матрицы равен четырем, а один из ее базисных миноров располагается на векторах a1, a2 , a3 , b1. Следовательно, эти векторы составляют

базис суммы L1 + L2 .

Если пространства L1 и L2 заданы однородными системами уравнений, то пересечение L1 ∩ L2 будет определяться системой, включаемую все уравнения

двух систем. Любая фундаментальная система решений такой системы уравнений дает базис пересечения L1 ∩ L2 .

Например, найдем базис пересечения подпространства L1 , заданного системой уравнений

x1 − x3 + x5 = 0,x2 − x4 + x6 = 0,x1 − x2 + x5 − x6 = 0,

и подпространства L2 , заданного системой уравнений

x2 − x − 3 + x6 = 0,x1 − x4 + x5 = 0.

Решение. Составим систему уравнений, состоящую из всех уравнений систем подпространств L1 и L2

x		− x	+ x = 0,
1	3	5
x2 − x4 + x6 = 0,
		− x2 + x5 − x6 = 0,
x1
x	2	− x − 3 + x	6	= 0,

		− x4 + x5 = 0
x1

и найдем ее общее решение

x = (x4 − x5 , x4 − x6 , x4 , x4 , x5 , x6 )T .

Здесь три свободных неизвестных: x4 , x5 , x6 . Поэтому каждая

фундаментальная система решений этой системы состоит из трех решений. Одну из фундаментальных систем решений составляют столбцы

243

1			−1		0
1			0
				−1
1	,		0	,		0
1		0		0	.

0			1			0

0			0			1

Они и представляют собой один из базисов подпространства L1 ∩ L2 . Если подпространства L1 и L2 заданы как линейные оболочки систем

векторов

L1 = a1, a2 , …, ak , L2 = b1, b2 , …, bl ,

то при построении базиса пересечения L1 ∩ L2 этих подпространств достаточно

перейти к описанию этих подпространств общими уравнениями, а затем действовать, как в последнем примере: объединяя две однородные системы в одну, искать фундаментальную систему решений объединенной системы.

Существуют и другие способы построения базиса пересечения. Например, можно составить векторное уравнение

α1a1 +α2a2 + … +αk ak = β1b1 + β2b2 + … + βl bl	(9.22)
с неизвестными α1, α2 , …, αk , β1, β2 , …, βl и от	него перейти к системе

покоординатных уравнений. Это линейная однородная система. Построив фундаментальную систему решений этой системы, для каждого решения из ФСР вычислим, например, левую часть векторного уравнения. Получим систему векторов, порождающую линейное пространство L1 ∩ L2 . Теперь базис в L1 ∩ L2

можно построить, выделив в этой системе максимальную линейно независимую подсистему. Отметим, что если система векторов a1, a2 , …, ak линейно

независима, то и построенная, как описано выше, система векторов, порождающая L1 ∩ L2 , будет линейно независимой. В этом случае дополнительно

выделять максимальную линейно независимую подсистему не нужно.

В заключение примем без доказательства теорему о размерности суммы линейных пространств.

Теорема 9.21 В конечномерном линейном пространстве V размерность суммы L1 + L2 подпространств L1 и L2 равна сумме размерностей этих

подпространств минус размерность их пересечения, т.е. dim(L1 + L2 )= dim L1 + dim L2 − dim(L1 ∩ L2 ).

244

9.10 Вопросы для самоконтроля

1Сформулируйте определение линейного пространства.

2Сформулируйте и докажите теорему о единственности нулевого элемента в линейном пространстве.

3Сформулируйте и докажите теорему о существовании единственного противоположного элемента линейного пространства.

4Докажите верность тождества 0x =θ для любого элемента линейного пространства.

5Докажите верность тождества −1 x = −x , для любого элемента линейного пространства.

6Докажите справедливость равенства αθ =θ .

7 Докажите, что если αx = 0 и α ≠ 0 , то x =θ .

8Докажите, что если αx = 0 , x =θ , то α = 0.

9Какое линейное пространство называется n -мерным? Как обозначается размерность пространства Vn ?

10Какое линейное пространство называется конечномерным? Приведите примеры конечномерных пространств.

11Какое линейное пространство называется бесконечномерным? Приведите примеры бесконечномерных пространств.

12Дайте определение базиса n -мерного линейного пространства. Приведите примеры базиса какого-нибудь линейного пространства.

13Сколько базисов может иметь линейное n -мерное пространство?

14Что означает разложение вектора x по базису?

15Сформулируйте и докажите теорему о единственности разложения любого вектора x пространства Vn по заданному базису.

16Какая матрица называется матрицей системы векторов в данном

базисе?

17Какая матрица называется матрицей перехода от базиса e1, e2 , …, en к

базису e1′, e2′ , …, en′ ?

18Выведите формулу (e1′, e2′ , …, en′ )= (e1, e2 , …, en )T T и объясните ее.

19Какую матрицу можно рассматривать как матрицу перехода от базиса к базису в n -мерном пространстве?

20Какие формулы называются формулами преобразования координат?

21Сформулируйте и докажите теорему о преобразовании координат?

22Какие два линейных пространства называются изоморфными?

23 Что означает понятия «образ», «прообраз», если V ~ U и x ↔ y , где x V , а y U .

24В каком случае два линейных пространства изоморфны?

25Сформулируйте и докажите утверждение о соответствии базисов изоморфных пространств.

26Сформулируйте определение подпространства линейного пространства.

245

27Какие подпространства заданного линейного пространства называются тривиальными?

28Приведите примеры нетривиальных подпространств линейных пространств.

29Расскажите о линейной зависимости (независимости) векторов.

30Сформулируйте и докажите основную теорему о линейной зависимости

векторов.

31Какие две системы векторов называются эквивалентными?

32Сформулируйте определение линейной оболочки системы векторов.

33Сформулируйте и докажите теорему о дополнении базиса подпространства до базиса всего n -мерного пространства.

34Сформулируйте и докажите теорему о том, что для любого линейного

подпространства L существует система линейных уравнений AX = 0 , в которой L — множество решений.

35 Какую систему линейных уравнений называют общими уравнениями подпространства?

36Что необходимо сделать для построения базиса подпространства, если последнее задано общими уравнениями?

37Какое уравнение называют параметрическим уравнением подпространства L в векторной форме?

38Напишите параметрические уравнения подпространства в координатной форме.

39Дайте определение пересечения подпространства L1 и L2 .

40Дайте определение суммы подпространства L1 и L2 .

41Какая сумма подпространств является прямой (обозначение)?

42Докажите утверждение о том, что сумма подпространств является подпространством.

43Какие подпространства L1 и L2 называются прямыми дополнениями

друг друга?

44Как найти какой-либо базис в подпространстве L1 + L2 ?

45Как найти какой-либо базис L1 ∩ L2 ?

246

Соседние файлы в предмете Алгебра и начала анализа

Источник

Подпространства линейного пространства

Определение линейного подпространства

Непустое подмножество линейного пространства называется линейным подпространством пространства , если

1) mathbf{u}+mathbf{v}in L~~forall mathbf{u,v}in L (подпространство замкнуто по отношению к операции сложения);

2) lambda mathbf{v}in L~~ forall mathbf{v}in L и любого числа lambda (подпространство замкнуто по отношению к операции умножения вектора на число).

Для указания линейного подпространства будем использовать обозначение Ltriangleleft V , а слово «линейное» опускать для краткости.

Замечания 8.7

1. Условия 1, 2 в определении можно заменить одним условием: lambda mathbf{u}+mu mathbf{v}in L~~ forall mathbf{u,v}in L и любых чисел lambda и . Разумеется, что здесь и в определении речь идет о произвольных числах из того числового поля, над которым определено пространство .

2. В любом линейном пространстве имеются два линейных подпространства:

а) само пространство , т.е. Vtriangleleft V ;

б) нулевое подпространство {mathbf{o}} , состоящее из одного нулевого вектора пространства , т.е. {mathbf{o}}triangleleft V . Эти подпространства называются несобственными, а все остальные — собственными.

3. Любое подпространство линейного пространства является его подмножеством: Ltriangleleft V~Rightarrow~Lsubset V , но не всякое подмножество Msubset V является линейным подпространством, так как оно может оказаться незамкнутым по отношению к линейным операциям.

4. Подпространство линейного пространства само является линейным пространством с теми же операциями сложения векторов и умножения вектора на число, что и в пространстве , поскольку для них выполняются аксиомы 1-8. Поэтому можно говорить о размерности подпространства, его базисе и т.п.

5. Размерность любого подпространства линейного пространства не превосходит размерности пространства Vcolon,dim{L}leqslant dim{V} . Если же размерность подпространства Ltriangleleft V равна размерности конечномерного пространства (dim{L}=dim{V}) , то подпространство совпадает с самим пространством: L=V .

Это следует из теоремы 8.2 (о дополнении системы векторов до базиса). Действительно, взяв базис подпространства , будем дополнять его до базиса пространства . Если это возможно, то dim{L}<dim{V} . Если нельзя дополнить, т.е. базис подпространства является базисом пространства , то dim{L}=dim{V} . Учитывая, что пространство есть линейная оболочка базиса (см. следствие 1 теоремы 8.1), получаем L=V .

6. Для любого подмножества линейного пространства линейная оболочка operatorname{Lin}(M) является подпространством и Msubset operatorname{Lin}(M)triangleleft V .

В самом деле, если M=varnothing (пустое множество), то по определению operatorname{Lin}(M)={mathbf{o}} , т.е. является нулевым подпространством и varnothingsubset{mathbf{o}}triangleleft V . Пусть Mnevarnothing . Нужно доказать, что множество замкнуто по отношению к операциям сложения его элементов и умножения его элементов на число. Напомним, что элементами линейной оболочки operatorname{Lin}(M) служат линейные комбинации векторов из . Так как линейная комбинация линейных комбинаций векторов является их линейной комбинацией, то, учитывая пункт 1, делаем вывод, что operatorname{Lin}(M) является подпространством , т.е. operatorname{Lin}(M)triangleleft V . Включение Msubset operatorname{Lin}(M) — очевидное, так как любой вектор mathbf{v}in M можно представить как линейную комбинацию 1cdotmathbf{v} , т.е. как элемент множества .

7. Линейная оболочка operatorname{Lin}(L) подпространства Ltriangleleft V совпадает с подпространством , т.е. operatorname{Lin}(L)=L .

Действительно, так как линейное подпространство содержит все возможные линейные комбинации своих векторов, то operatorname{Lin}(L)subset L . Противоположное включение (Lsubset operatorname{Lin}(L)) следует из пункта 6. Значит, operatorname{Lin}(L)=L .

Примеры линейных подпространств

Укажем некоторые подпространства линейных пространств, примеры которых рассматривались ранее. Перечислить все подпространства линейного пространства невозможно, за исключением тривиальных случаев.

1. Пространство {mathbf{o}} , состоящее из одного нулевого вектора пространства , является подпространством, т.е. {mathbf{o}}triangleleft V .

2. Пусть, как и ранее, V_1,,V_2,,V_3 — множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно. Если прямая принадлежит плоскости, то V_1triangleleft V_2triangleleft V_3 . Напротив, множество единичных векторов не является линейным подпространством, так как при умножении вектора на число, не равное единице, получаем вектор, не принадлежащий множеству.

3. В n-мерном арифметическом пространстве $mathbb{R}^n$ рассмотрим множество «полунулевых» столбцов вида $x=begin{pmatrix} x_1&cdots& x_m&0&cdots&0end{pmatrix}^T$ с последними (n-m) элементами, равными нулю. Сумма «полунулевых» столбцов является столбцом того же вида, т.е. операция сложения замкнута в . Умножение «полунулевого» столбца на число дает «полунулевой» столбец, т.е. операция умножения на число замкнута в . Поэтому $Ltriangleleft mathbb{R}^n$ , причем dim{L}=m . Напротив, подмножество ненулевых столбцов $mathbb{R}^n$ не является линейным подпространством, так как при умножении на нуль получается нулевой столбец, который не принадлежит рассматриваемому множеству. Примеры других подпространств $mathbb{R}^n$ приводятся в следующем пункте.

4. Пространство {Ax=o} решений однородной системы уравнений с неизвестными является подпространством n-мерного арифметического пространства $mathbb{R}^n$ . Размерность этого подпространства определяется матрицей системы: dim{Ax=o}=n-operatorname{rg}A .

Множество {Ax=b} решений неоднородной системы (при bne o ) не является подпространством $mathbb{R}^n$ , так как сумма двух решений неоднородной ; системы не будет решением той же системы.

5. В пространстве $M_{ntimes n}$ квадратных матриц порядка л рассмотрим два подмножества: множество $M_{ntimes n}^{text{sim}}$ симметрических матриц и множество $M_{ntimes n}^{text{kos}}$ кососимметрических матриц. Сумма симметрических матриц является симметрической матрицей, т.е. операция сложения замкнута в $M_{ntimes n}^{text{sim}}$ . Умножение симметрической матрицы на число также не нарушает симметричность, т.е. операция умножения матрицы на число замкнута в $M_{ntimes n}^{text{sim}}$ . Следовательно, множество симметрических матриц является под пространством пространства квадратных матриц, т.е. $M_{ntimes n}^{text{sim}}triangleleft M_{ntimes n}$ . Нетрудно найти размерность этого подпространства. Стандартный базис образуют : л матриц с единственным ненулевым (равным единице) элементом на глав ной диагонали: $a_{ii}=1~ i=1,ldots,n$ , а также матрицы с двумя ненулевыми (равными единице) элементами, симметричными относительно главной диагонали: $a_{ij}=a_{ji}=1,$ i=1,ldots,n, j=i,i+1,ldots,n . Всего в базисе будет ${n+(n-1)+ldots+2+1= frac{n(n+1)}{2}}$ матриц. Следовательно, $dim{M_{ntimes n}^{text{sim}}}= frac{n(n+1)}{2}$ . Аналогично получаем, что $M_{ntimes n}^{text{kos}}triangleleft M_{ntimes n}$ и $dim{M_{ntimes n}^{text{kos}}}= frac{n(n+1)}{2}$ .

Множество вырожденных квадратных матриц n-го порядка не является подпространством $M_{ntimes n}$ , так как сумма двух вырожденных матриц может оказаться невырожденной матрицей, например, в пространстве $M_{2times2}:$

$begin{pmatrix}1&0\0&0end{pmatrix}+ begin{pmatrix}0&0\0&1end{pmatrix}= begin{pmatrix}1&0\0&1end{pmatrix}!.$

6. В пространстве многочленов P(mathbb{R}) с действительными коэффициентами можно указать естественную цепочку подпространств

$P_0(mathbb{R})triangleleft P_1(mathbb{R})triangleleft P_2(mathbb{R})triangleleft ldots triangleleft P_n(mathbb{R})triangleleft ldots triangleleft P(mathbb{R}).$

Множество четных многочленов (p(-x)=p(x)) является линейным подпространством P(mathbb{R}) , так как сумма четных многочленов и произведение четно го многочлена на число будут четными многочленами. Множество нечетных многочленов (p(-x)=-p(x)) также является линейным пространством. Множество многочленов, имеющих действительные корни, не является линейным подпространством, так как при сложении таких двух многочленов может получиться многочлен, который не имеет действительных корней, например, (x^2-x)+(x+1)=x^2+1 .

7. В пространстве C(mathbb{R}) можно указать естественную цепочку подпространств:

$C(mathbb{R})triangleright C^1(mathbb{R})triangleright C^2(mathbb{R}) triangleright ldotstriangleright C^m(mathbb{R})trianglerightldots$

Многочлены из P(mathbb{R}) можно рассматривать как функции, определенные на . Так как многочлен является непрерывной функцией вместе со своими производными любого порядка, можно записать: P(mathbb{R})triangleleft C(mathbb{R}) и $P_n(mathbb{R})triangleleft C^m(mathbb{R})$ forall m,ninmathbb{N} . Пространство тригонометрических двучленов $T_{omega} (mathbb{R})$ является подпространством $C^m(mathbb{R})$ , так как производные любого порядка функции f(t)=asinomega t+bcosomega t непрерывны, т.е. $T_{omega}(mathbb{R})triangleleft C^m(mathbb{R})$ forall min mathbb{N} . Множество непрерывных периодических функций не является подпространством C(mathbb{R}) , так как сумма двух периодических функций может оказаться непериодической функцией, например, sin{t}+sin(pi t) .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λx∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Пусть L и M — два подпространства пространства R.

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

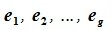
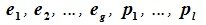
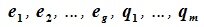
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

(6.1)

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

(6.2)

Тогда

(6.3)

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

(6.5)

Из уравнений (6.4) и (6.5) имеем:

(6.6)

или

(6.7)

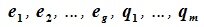
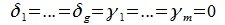
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

(6.8)

В силу линейной независимости базиса подпространства L имеем:

(6.9)

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

(6.10)

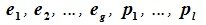
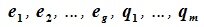
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов а y — линейной комбинацией векторов. Следовательно векторы (6.10) порождают подпространство F. Получили, что векторы (6.10) образуют базис F=L+M.

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

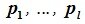
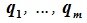
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

(6.11)

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

(6.12)

или

(6.13)

Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M=0, то

(6.14)

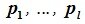
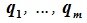
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

(6.15)

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

(6.16)

Из (6.16) имеем:

(6.17)

(6.18)

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:

(6.19)

Вычитая (6.19) из (6.17), получим

или

(6.20)

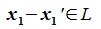
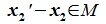
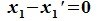
Так как , и L∩M=0, то и . Следовательно и . ■

Источник

Линейные и евклидовы пространства
- Определение линейного пространства
- Примеры линейных пространств
- Простейшие свойства линейных пространств
Линейные подпространства
- Примеры линейных подпространств
- Свойства линейного подпространства
- Сумма и пересечение линейных подпространств
- Свойства пересечения и суммы линейных подпространств
Линейная оболочка
- Основные свойства линейной оболочки
Линейная зависимость
- Базис. Размерность
- Замена базиса
- Свойства матрицы перехода
Евклидовы пространства
- Метод ортогонализации
Ортогональное дополнение
- Свойства ортогонального дополнения
- Унитарные пространства

Евклидово пространство — это вещественное линейное пространство, в котором зафиксирована симметричная положительно определенная билинейная форма. Значение билинейной формы на паре элементов называется скалярным произведением этих векторов.

Линейные и евклидовы пространства

Определение линейного пространства

Определение:

Множество V элементов х, у, z,… называется линейным пространством (действительным или комплексным), если по некоторому правилу

I. любым двум элементам х и у из V поставлен в соответствие элемент из V, обозначаемый х + у и называемый суммой элементов х и у;

II. любому элементу х из V и каждому числу а (вещественному или комплексному) поставлен в соответствие элемент из V, обозначаемый ах и называемый произведением элемента х на число а, и эти правила сложения и умножения на число удовлетворяют следующим аксиомам:

(х + у) + z = х + (у + z) (ассоциативность);
х + у = у + х (коммутативность)-,
во множестве V существует элемент θ такой, что для любого элемента х из V выполняется равенство х + θ = х;
для любого элемента х из V во множестве V существует элемент (-х) такой, что х + (-х) = θ;
а(х + у) = ах + ау;
(а + β)х = ах + βх;
а( β х) = (а β )х;
1х = х.

Элемент θ называется нулевым элементом, а элемент (-х) — противоположным элементу х.
Элементы х, у, z,… линейного пространства часто называют векторами. Поэтому линейное пространство называют также векторным пространством.

Примеры линейных пространств

Совокупность свободных геометрических векторов V3 в пространстве с введенными операциями сложения векторов и умножения вектора на число (рис. 1).

Этим же свойством обладают: совокупность V1 векторов на прямой и совокупность V2 векторов на плоскости.

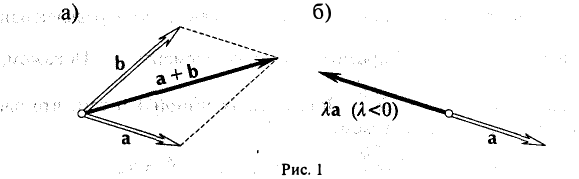
2, Совокупность упорядоченных наборов () из n действительных чисел.

Операции — сложение и умножение на действительное число — вводятся так:

а) сложение —

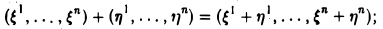
б) умножение на число —

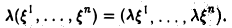
Обозначение: Rn (n -мерное вещественное координатное пространство).

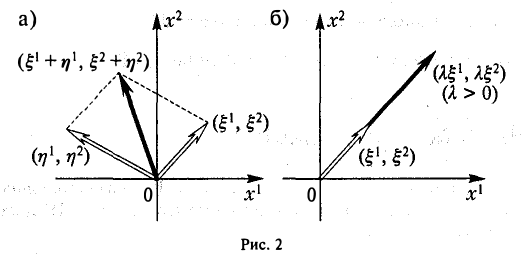
3. Совокупность всевозможных матриц Rmxn размера m х n с введенными правилами сложения матриц,

и умножения матрицы на число,

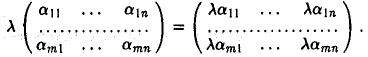
В частности, совокупность n-строк, R1xn и совокупность столбцов высоты m, Rmx1, являются линейными пространствами.

4. Множество С(-1, 1) вещественных функций, непрерывных на интервале (-1, I), с естественными операциями сложения функций и умножения функции на число.

Во всех приведенных примерах требования 1-8 проверяются непосредственно.

Простейшие свойства линейных пространств

Нулевой элемент θ определен однозначно.

Пусть θ1 и θ2 — нулевые элементы пространства V. Рассмотрим их сумму θ1 + θ2. Вследствие того, что θ2 — нулевой элемент, из аксиомы 3 получаем, что θ1+ θ2 = θ1, а так как элемент θ1 — также нулевой, то θ1 + θ2 = θ2 + θ1 = θ2 , т. е. θ1 = θ2 .

2. Для любого элемента х противоположный ему элемент (—х) определен однозначно.

Пусть x^— и х_ — элементы, противоположные элементу х. Покажем, что они равны.

Рассмотрим сумму х_ + х + x^— . Пользуясь аксиомой 1 и тем, что элемент x^— противоположен элементу х, получаем:

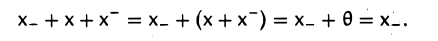
Аналогично убеждаемся в том, что

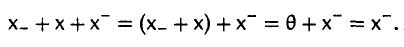
Нетрудно убедится также в справедливости следующих свойств:

Для любого элемента х выполняется равенство 0х = θ.
Для любого элемента х выполняется равенство —х = (- 1)х.
Для любого числа а выполняется равенство аθ = θ.
Из того, что ах = θ, следует, что либо а = 0, либо х = θ.

Линейные подпространства

Непустое подмножество W линейного пространства V называется линейным подпространством пространства V, если для любых элементов х и у из W и любого числа а выполняются следующие условия:

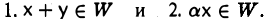
Иногда говорят: «множество W замкнуто относительно указанных операций».

Примеры линейных подпространств

1.Множество векторов на плоскости V2 является линейным подпространством линейного пространства V3.

2. Совокупность решений однородной системы m линейных уравнений с n неизвестными

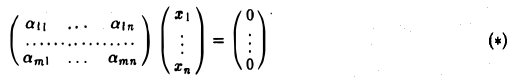
образует линейное подпространство линейного пространства Rnx1. В самом деле, сумма решений однородной системы () является решением этой же системы и произведение решения системы (*) на число также является ее решением.

3. Совокупность всех вещественнозначных функций, непрерывных на интервале (-1, 1) и обращающихся в нуль при t = 0, образует линейное подпространство линейного пространства С(— 1,1).

Сумма f(t) + g(t) функций f(t) и g(t), обращающихся в нуль при t = 0, t(0) = f(0) = 0, и произведение af(t) функции f(t), обращающейся в нуль при t = 0, f(0) = 0, на число а равны нулю при t = 0.

Свойства линейного подпространства

Если x1, …, хq — элементы линейного подпространства W, то любая их линейная комбинация также лежит в W.
Линейное подпространство W само является линейным пространством.

Достаточно убедиться лишь в том, что нулевой элемент 0 и элемент, противоположный произвольному элементу из W, лежат в W. Указанные векторы получаются умножением произвольного элемента х ∈ W на 0 и на -1: θ = 0х, -х = (- 1)х.

Сумма и пересечение линейных подпространств

Пусть V — линейное пространство, W1 w W2 — его линейные подпространства. Суммой W1 + W2 линейных подпространств W1 и W2 называется совокупность всевозможных элементов х пространства V, которые можно представить в следующем виде

где x1 лежит в W1, а х2 — в W2. Коротко это можно записать так:

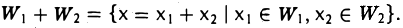
Сумма линейных подпространств W1 и W2 нaзывается прямой, если для каждого элемента х этой суммы разложение (1) единственно (рис. 3).

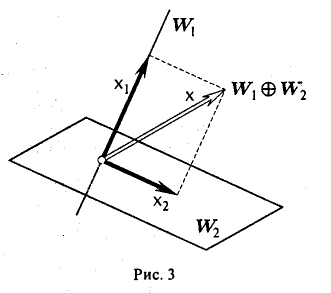
Обозначение: W1⊕W2

Пересечением W1 ∩ W2 линейных подпространств W1 и W2 линейного пространства V называется совокупность элементов, которые принадлежат одновременно и линейному подпространству W1, и линейному подпространству W2.

Свойства пересечения и суммы линейных подпространств

Сумма W1 + W2 является линейным подпространством пространства V.

Возьмем в W1 + W2 два произвольных элемента х и у. По определению суммы подпространств найдутся элементы х1, у1, из W1 и х2, у2, из W2 такие, что

Это позволяет записать сумму х + у в следующем виде

Так как то сумма х + у лежит в W1 + W2.

Аналогично доказывается включение ах ∈ W1 + W2.

2. Пересечение W1 ∩ W2 является линейным подпространством пространства V.

3. Если нулевой элемент является единственным общим вектором подпространств W1 й W2 линейного пространства V, то их сумма является прямой — W1 ⊕ W2.

Линейная оболочка

Линейной оболочкой L(X) подмножества X линейного пространства V называется совокупность всевозможных линейных комбинаций элементов из X,

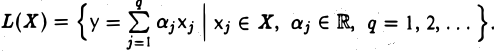
Последнее читается так: «линейная оболочка L(X) состоит из всевозможных элементов у, представимых в виде линейных комбинаций элементов множества X».

Основные свойства линейной оболочки

Линейная оболочка L(X) содержит само множество X.
L(X) — линейное подпространство пространства V.

Сумма линейных комбинаций элементов множества X и произведение линейной комбинации элементов на любое число снова являются линейными комбинациями элементов множества X.

3. L(X) — наименьшее линейное подпространство, содержащее множество X.

Это свойство следует понимать так: если линейное подпространство W содержит множество X , то W содержит и его линейную оболочку L(X).

Пусть W — линейное подпространство, содержащее заданное множество X. Тогда произвольная линейная комбинация 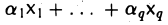элементов множества X — элемент линейной оболочки L(X) — содержится и в подпространстве W.

Пример:

Рассмотрим в линейном пространстве R3 две тройки ξ = (1,1,0) и η = (1,0, I) (рис.4). Множество решений уравнения

является линейной оболочкой L(ξ , η) троек ξ и η.
Действительно, тройки (I, 1, 0) и (1, 0, I) образуют фундаментальную систему решений однородного уравнения (2), и значит, любое решение этого уравнения является их линейной комбинацией.

Пример:

Рассмотрим в линейном пространстве С(- ∞, ∞) вещественнозначных функций, непрерывных на всей числовой оси, набор X одночленов 1, х,…, хn:

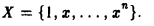
Линейная оболочка L(X) представляет собой совокупность многочленов с вещественными коэффициентами, степени которых не превосходят n.

Обозначение:

Линейная зависимость

Определение. Система элементов х1 . .. , хq линейного пространства V называется линейно зависимой, если найдутся числа a1,… , аq, не все равные нулю и такие, что
(1)

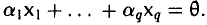
Если равенство (1) выполняется только при а1 = … = аq = 0, то система элементов x1,…, хq называется линейно независимой.

Справедливы следующие утверждения.

Теорема:

Система элементов x1,…, хq (q ≥ 2) линейно зависима в том и только в том случае, если хотя бы один из ее элементов можно представить в виде линейной комбинации остальных.

Предположим сначала, что система элементов x1,…, xq линейно зависима. Будем Считать для определенности, что в равенстве (1) отличен от нуля коэффициент аq. Перенося все слагаемые, кроме последнего, в правую часть, после деления на аq ≠ 0 получим, что элемент хq является линейной комбинацией элементов х1 …, хq:

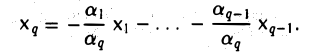
Обратно, если один из элементов равен линейной комбинации остальных,

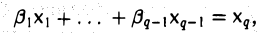
то, перенося его в левую часть, получим линейную комбинацию

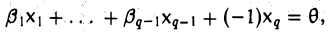
в которой есть отличные от нуля коэффициенты (-1 ≠ 0). Значит, система элементов x1,…., хq линейно зависима.

Теорема:

Пусть система элементов х1,…,хq линейно независима и y=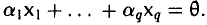. Тогда коэффициенты a1 ,… ,аq определяются по элементу у единственным образом.
Пусть

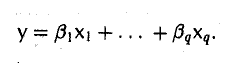
Тогда

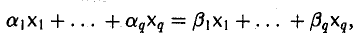
откуда

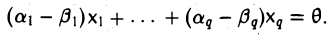
Из линейной независимости элементов x1…, xq вытекает, что a1 — β1 = … = аq — βq = 0 и, значит,

Теорема:

Система элементов, содержащая линейно зависимую подсистему, линейно зависима.
Пусть первые q элементов системы х1 … , хq, xq+1… , xm линейно зависимы. Тогда найдется линейная комбинация этих элементов такая, что

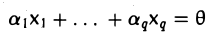
и не все коэффициенты а1 … ,аq равны нулю. Добавляя элементы xq+1… , xm с нулевыми множителями, получаем, что и в линейной комбинации

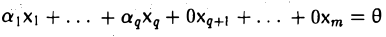
равны нулю не все коэффициенты.

Пример. Векторы из V2 линейно зависимы тогда и только тогда, когда они компланарны (рис.5).

Базис. Размерность

Упорядоченная система элементов e1,…, еn линейного пространства V называется базисом этого линейного пространства, если элементы e1,…, еn линейно независимы и каждый элемент из V можно представить в виде их линейной комбинации. Упорядоченность означает здесь, что каждому элементу приписан определенный (порядковый) номер. Из одной системы п элементов можно построить n! упорядоченных систем.

Пример:

Пусть a, b, с — тройка некомпланарных векторов из Vз (рис.6). Тогда упорядоченные тройки а, b, с; b, с, а; с, а, b; b, а, с; а, с, b и с, b, а — различные базисы V3.

Пусть с = (e1 … еn) — базис пространства V.

Тогда для любого элемента х из V найдется набор чисел такой, что

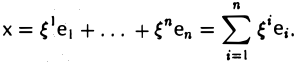
В силу теоремы 2 числа — координаты элемента х в базисе с — определены однозначно.

Посмотрим, что происходит с координатами элементов при простейших действиях с ними.

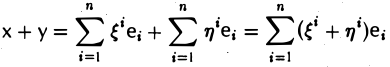
и для любого числа а

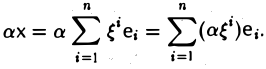
Таким образом, при сложении элементов их соответствующие координаты складываются, а при умножении элемента на число все его координаты умножаются на это число.

Координаты элемента часто удобно записывать в виде столбца. Например,

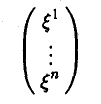
— координатный столбец элемента 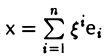в базисе e.

Разложим произвольную систему элементов x1,…, хq по базису e,

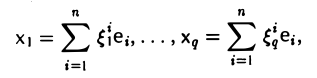
ли рассмотрим координатные столбцы элементов ч1,…, хq в этом базисе:

Теорема:

Система элементов х1,… ,хq линейно зависима тогда и только тогда, когда линейно зависима система их координатных столбцов в каком-нибудь базисе.

Пусть

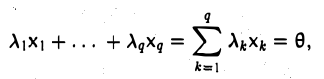
причем хотя бы один из коэффициентов λk отличен от нуля. Запишем это подробнее

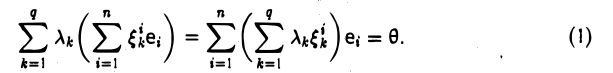
Отсюда в силу единственности разложения элемента по базису вытекает, что

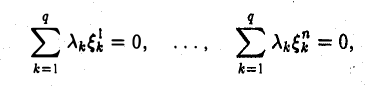
или, что тоже,

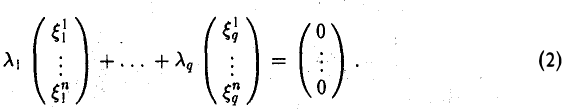
Таким образом, линейная комбинация координатных столбцов элементов x1,…, xq равна нулевому столбцу (с теми же коэффициентами λ1,…, λg). Это и означает, что система координатных столбцов линейно зависима.

Если же выполняется равенство (2), то, проводя рассуждения в обратном порядке, получаем формулу (1).

Тем самым, обращение в нуль некоторой нетривиальной (хотя бы один из коэффициентов отличен от нуля) линейной комбинации элементов линейного пространства равносильно тому, что нетривиальная линейная комбинация их координатных столбцов (с теми же коэффициентами) равна нулевому столбцу.

Теорема:

Пусть базис с линейного пространства V состоит из п элементов. Тогда всякая система из то элементов, где т > п, линейно зависима.

4 В силу теоремы 3 достаточно рассмотреть случай m = п + 1.

Пусть x1,.. . ,хп+1 — произвольные элементы пространства V. Разложим каждый элемент по базису e = (е1 …, еп):

и запишем координаты элементов х1 …, xn+1 в виде матрицы, отводя j-й столбец координатам элемента xj, j = 1,…, п + 1. Получим матрицу из п строк и п + 1 столбцов —

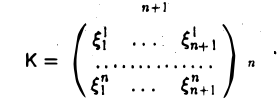
Ввиду того, что ранг матрицы К не превосходит числа п ее строк, столбцы матрицы К (их п + 1) линейно зависимы. А так как это координатные столбцы элементов x1…..хп+1, то согласно теореме 4 система элементов x1…..хп+1 также линейно зависима.

Следствие:

Все базисы линейного пространства V состоят из одинакового числа элементов.
Пусть базис e состоит из п элементов, а базис e’ из п‘ элементов. В силу только что доказанной теоремы из линейной независимости системы е’1,…, е’n заключаем, что п’ ≤ п. Меняя базисы e и e’ местами, в силу этой же теоремы получаем, что п ≤ п’.

Тем самым, п = п’.
Размерностью линейного пространства V называется число элементов базиса этого пространства.

Пример:

Базис координатного пространства R» образуют элементы

Система элементов e1,e2, …,еп линейно независима: из равенства

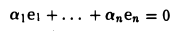
получаем, что

и значит, a1 = … = an = 0.

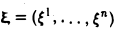
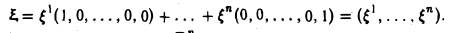
Кроме того, любой элемент из R» можно записать в виде линейной комбинации элементов e1…..еп: ‘

Тем самым, размерность пространства R» равна п.

Пример:

Однородная линейная система

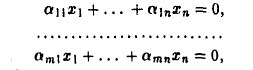
имеющая ненулевые решения, обладает фундаментальной системой решений (ФСР). ФСР является базисом линейного пространства решений однородной системы. Размерность этого линейного пространства равна числу элементов ФСР, т.е. п — r, где r — ранг матрицы коэффициентов однородной системы, an — число неизвестных.

Пример:

Размерность линейного пространства Мп многочленов степени не выше п равна п + I.

Так как всякий многочлен P(t) степени не выше п имеет вид

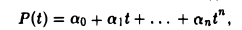
то достаточно показать линейную независимость элементов

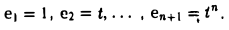
Рассмотрим равенство

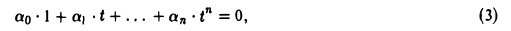
где t произвольно. Полагая t = 0, получаем, что ао = 0.

Продифференцируем равенство (3) по t:

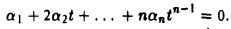
Вновь положив t = 0, получим, что a1 = 0.

Продолжая этот процесс, последовательно убеждаемся в том, что a0 = a1 = … = ап = 0. Это означает, что система элементов e1 = I,… ,en+1 = t» линейно независима. Следовательно, искомая размерность равна n + 1.

Линейное пространство, размерность которого равна п, называется п-мерным.

Обозначение: dim V = п.

Соглашение. Далее в этой главе всюду считается, если не оговорено противное, что размерность линейного пространства V равна п.

Ясно, что если W — подпространство n-мерного линейного пространства V, то dim W ≤ п.

Покажем, что в п-мерном линейном пространстве V есть линейные подпространства любой размерности k ≤ п.

Пусть e = (е1 … еn) — базис пространства V. Легко убедиться в том, что линейная оболочка

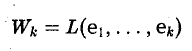
имеет размерность k.

По определению dim{ θ } = 0.

Теорема:

О пополнении базиса. Пусть система элементов а1.. , аk линейного пространства V размерности п линейно независима и к < п. Тогда в пространстве V найдутся элементы такие, что система а1 … , аk, — базис V.
Пусть b — произвольный элемент линейного пространства V. Если система а1…. , аk, b линейно зависима, то

так как в нетривиальной линейной комбинации

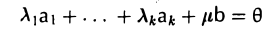
коэффициент μ ≠ 0 вследствие линейной независимости системы а1…., аk.

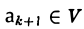
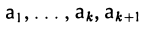
Если бы разложение вида (4) можно было бы написать для любого элемента b пространства V, то исходная система a1…, аk была бы базисом согласно определению. Но в силу условия k < п это невозможно. Поэтому должен существовать элемент такой, что пополненная система будет линейно независимой.

Если k + 1 = п, то эта система — базис пространства V.

Если k + 1 < п, то для системы 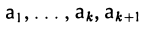следует повторить предыдущие рассуждения.

Таким способом любую заданную линейно независимую систему элементов можно достроить до базиса всего пространства V.

Пример:

Дополнить систему из двух векторов а1 = (1,2,0,1), а2 = (-1,1.1,0) пространства R4 до базиса этого пространства.

Возьмем в пространстве R4 векторы a3 = (1,0,0,0) и а4 = (0, 1,0,0) и покажем, что система векторов a1,а2,а3,а4 — базис R4.

Ранг матрицы

строками которой являются координаты векторов а1, а2, а3, а4, равен четырем. Это означает, что строки матрицы А, а, значит, и векторы а1, а2, а3, а4 линейно независимы.

Подобный подход используется и в общем случае: чтобы дополнить систему k линейно независимых элементов

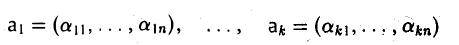
до базиса пространства R» , матрица

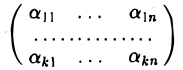
элементарными преобразованиями строк приводится к трапециевидной форме, а затем дополняется п — k строками вида

(0 … 1 … 0)

так, чтобы ранг получаемой матрицы был равен п. Справедливо следующее утверждение.

Теорема:

Пусть W1 и W2 — линейные подпространства линейного пространства V. Тогда

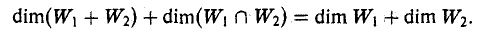
Замена базиса

Пусть e = (e1 … еn) и e’ = (е’1, … е’n) — базисы линейного пространства V. Разложим элементы базиса e’ по базису с. Имеем

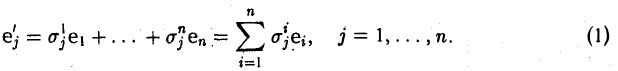
Эти соотношения удобно записать в матричной форме
(2)

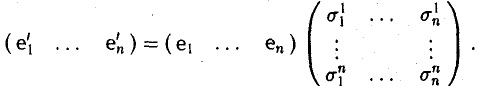
Матрица

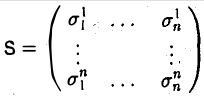
называется матрицей перехода от базиса e к базису e’.

Свойства матрицы перехода

det S ≠ 0.

Доказательство этого свойства проводится от противного.

Из равенства detS = 0 вытекает линейная зависимость столбцов матрицы S. Эти столбцы являются координатными столбцами элементов е’1,…, е’n в базисе e. Поэтому (и вследствие теоремы 4) элементы е’1…..с’n должны быть линейно зависимыми.

Последнее противоречит тому, что e’ — базис. Значит, допущение, что det S = 0, неверно.

2. Если и 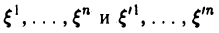— координаты элемента х в базисах e и e’ соответственно, то:
(3)

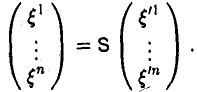
Заменяя в формуле

e’j их выражениями (1), получаем, что

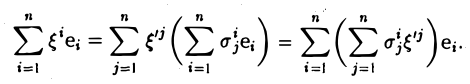
Отсюда в силу единственности разложения элемента по базису имеем

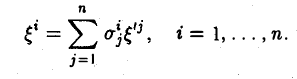
Переходя к матричной записи найденных равенств, убеждаемся в справедливости свойства 2.

3. S ^-1 — матрица перехода от базиса e’ к базису e.

Свойство 3 доказывается умножением обеих частей матричного равенства (2) на матрицу S^-1 справа.

Евклидовы пространства

Вещественное линейное пространство V называется (вещественным) евклидовым пространством, если любым двум элементам х и у из V ставится в соответствие число, обозначаемое через (х,у), такое, что для любых элементов х, y,z и произвольного вещественного числа а выполняются следующие условия:

4. (х, х) ≥ 0; причем равенство нулю возможно в том и только в том случае, если х = θ.

Число (х, у) называется скалярным произведением элементов х и у. Примеры евклидовых пространств.

В пространстве свободных векторов К] скалярное произведение векторов а и b определяется так:

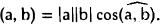
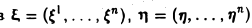
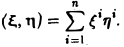
2. Скалярное произведение произвольных элементов из координатного пространства R» можно определить формулой

3, Линейное подпространство евклидова пространства само является евклидовым пространством.

Пользуясь определением евклидова пространства, нетрудно доказать следующие свойства:

Теорема:

Неравенство Коши—Буняковского. Для любых двух элементов х и у евклидова пространства V справедливо неравенство

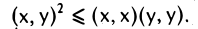
Если (х, х) = θ , то х = θ и неравенство выполняется вследствие того, что ( θ , у) = 0.

Обратимся к случаю (х, х) ≠ 0. Тогда (х, х) > 0. По определению скалярного произведения неравенство

справедливо для любых элементов х и у из пространства V и любого вещественного числа t. Запишем неравенство (1) подробнее:

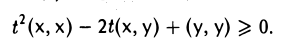
Левую часть последнего неравенства можно рассматривать как квадратный трехчлен относительно t. Из того, что знак этого квадратного трехчлена не изменяется при любых t, заключаем, что его дискриминант неположителен,

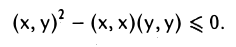
Перенося вычитаемое в правую часть, получаем требуемое неравенство.

Замечание:

Часто доказанное неравенство записывают в равносильной форме,

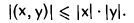
Следует подчеркнуть, что слева в этом неравенстве стоит абсолютная величина (модуль) скалярного произведения, а в правой части — нормы векторов х и у.

Определение:

Длиной (нормой) элемента х называется число |х|, вычисляемое по правилу

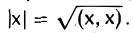
Ясно, что |х| ≥ 0 для любого х, причем равенство |х| = 0 возможно лишь в случае, если х = θ.

Рассмотрим цепочку равенств:

Заменяя второе слагаемое на 2|(х, у)| ≥ 2(х, у) и применяя неравенство Коши—Буняковского |(х,у)| ≤ |х| • |у|, получаем, что

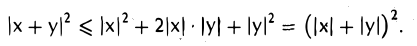
После извлечения квадратного корня приходим к неравенству треугольника:
|х + у| ≤ |х| + |у|
(рис.7).

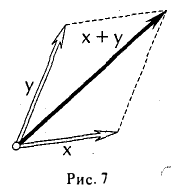
Углом между ненулевыми элементами х и у евклидова пространства называется число φ, подчиненное следующим двум условиям:

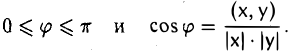
Определение угла корректно, так как согласно теореме 8 имеем

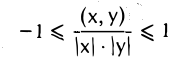
для любых ненулевых элементов х и у.

Элементы х и у называются ортогональными, если (х, у) = 0. Для ортогональных элементов из соотношения (2) вытекает равенство

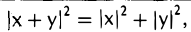
являющееся обобщением известной теоремы Пифагора’, квадрат длины суммы ортогональных элементов равен сумме квадратов их длин (рис. 8).

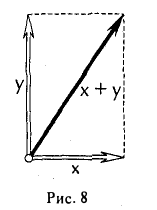
Система элементов f1…..f k называется ортогональной, если (fi, fj) =0′ при i ≠ j, и ортонормированной, если

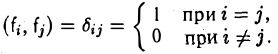
Определение:

Символ

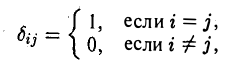
называют символом Кронекера.

Теорема:

Ортонормированная система элементов линейно независима.

Умножая обе части равенства

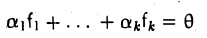
скалярно на элемент fj, j = 1 ,… ,k, получаем, что

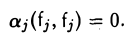
И так как (fj, fj) = 1,то aj = 0, j = 1,…, k.

Метод ортогонализации

Покажем, как, пользуясь заданной системой линейно независимых элементов f1,… ,fk евклидова пространства Е, построить в нем ортонормированную систему из к элементов.

Положим g1 = f1.

Для того, чтобы элемент

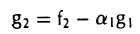
был ортогонален элементу g1, необходимо выполнение следующего равенства:

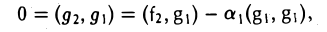
откуда

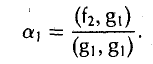
Тем самым, элемент

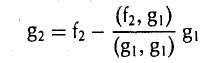
ортогонален элементу g1 (рис. 9 а).

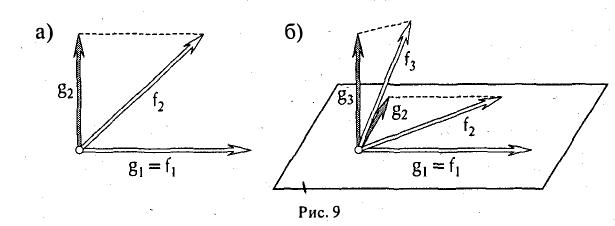
Пользуясь построенными элементами g1, g2 и заданным элементом fз, построим элемент

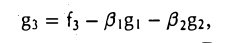
ортогональный как элементу g1, так и элементу g2. Для этого коэффициенты β1 и β2 должны удовлетворять следующим условиям:

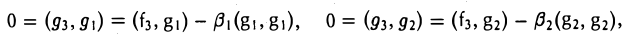
откуда

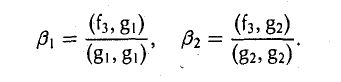
Таким образом, элемент
, (f3,g|) (f3,g2)

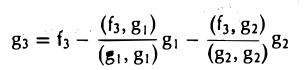
ортогонален элементам g1 и g2 (рис. 9 6).

Аналогичными рассуждениями можно показать, что элемент

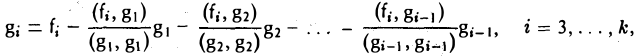
ортогонален элементам

Делением каждого элемента gi (i = 1…..k) на его длину |g<|, получаем ортонормированную систему

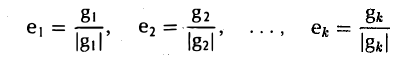
(рис. 10).

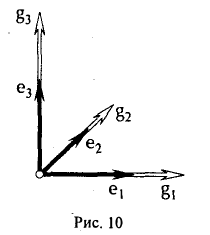
Базис e = (e1 … еn) евклидова пространства называется ортонормированным, или ортобазисом, если

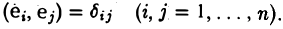
Суммируя вышеизложенное, получаем следующий результат.

Теорема:

В любом евклидовом пространстве существует о ртонормированный базис.
Пример:

Методом ортогонализации построить ортоиормированный базис евклидова пространства Е по его базису

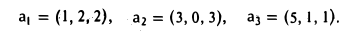
Полагаем b1 = a1 и b2 = а2 — ab1. Для того, чтобы вектор

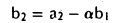
был ортогонален вектору b1, необходимо выполнение неравенства

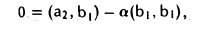
откуда

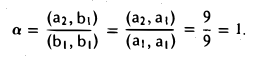
Тем самым,

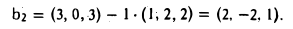
Для того, чтобы вектор

был ортогонален векторам b1 и b2, необходимо выполнение равенств

откуда

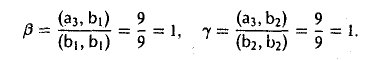
Тем самым, вектор

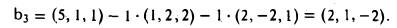
Система векторов b1, b2, b3 ортогональна. Поделив каждый вектор на его длину, получим

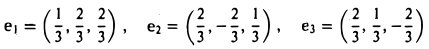
— ортонормированный базис пространства Е.

При помощи ортонормированного базиса скалярное произведение элементов вычисляется особенно просто. Пусть e = (e1 … еn) — ортонормированный базис пространства Е. Вычислим скалярное произведение элементов х и у, предварительно разложив их по базису e

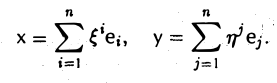
Имеем

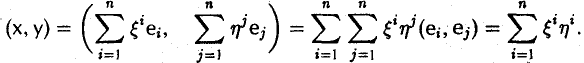
В частности,

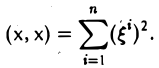
Откуда

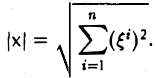
Ортогональное дополнение

Пусть W — линейное подпространство евклидова пространства V. Совокупность W⊥ элементов у пространства V, обладающих свойством

(y. х) = 0,

где х — произвольный элемент из W, называется ортогональным дополнением подпространства W. Другими словами, ортогональное дополнение W⊥ состоит из всех элементов у, ортогональных всем элементам подпространства W.

Свойства ортогонального дополнения

W⊥ — линейное подпространство пространства V. Пусть элементы y1, у2 лежат в W⊥ , т. е.

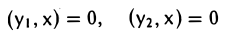
для любого элемента х из W. Складывая эти равенства и пользуясь свойствами скалярного произведения, получаем,что

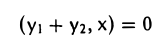
для любого элемента х из W. Это означает, что

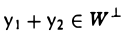
Из того, что (у, х) = 0 для любого элемента х из W, вытекает равенство (ау, х) = а(у, х) и, значит, включение ay ∈ W⊥ .

V = W ⊕ W⊥ .

Свойство 2 означает, что любой элемент х пространства V можно представить, причем единственным образом, в виде суммы элементов из W и W⊥ :

x = y+z. ‘ (*)

Элемент у ∈ W называется ортогональной проекцией элемента х на линейное подпространство W, а элемент z ∈ W⊥ — его ортогональной составляющей (рис. 11).

Покажем, как по заданным элементу х и линейному подпространству W найти его ортогональную проекцию у и ортогональную составляющую г.

Можно считать, что в линейном подпространстве W задан ортонормированный базис e1…..еk. Запишем искомый элемент у в виде линейной комбинации

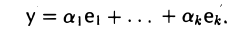
Подставляя это выражение в формулу (*):

и умножая обе части полученного равенства последовательно на элементы e1,…, еk, в предположении z ⊥ W приходим к соотношениям

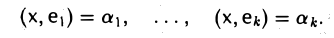
Элементы

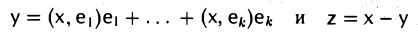
обладают требуемыми свойствами. *

Пример:

Найти ортогональную проекцию вектора х = (4, 2, 3, 5) на линейное подпространство W ⊂ R4, заданное системой уравнений

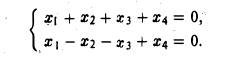
Векторы a1 = (1,0,0,-1) и а2 = (0,1,-1,0) образуют фундаментальную систему решений и, следовательно, базис подпространства W. Кроме того, векторы a1 и а2 ортогональны. Для того, чтобы построить ортонормированный базис подпространства W, достаточно разделить эти векторы на иx длины. В результате получим

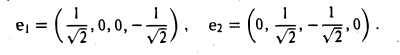
Вектор

является ортогональной проекцией вектора х = (4,2, 3, 5), на подпространство W, а вектор

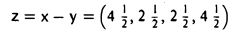
— его ортогональной составляющей.

Унитарные пространства

Унитарным пространством называется линейное комплексное пространство U, в котором каждой упорядоченной паре элементов х и у из U ставится в соответствие число — скалярное произведение (х, у) так, что для любых элементов х, у и z из U и любого комплексного числа а выполняются следующие соотношения:

(у, х) = (х, у) (черта в правой части указывает на операцию комплексного сопряжения);
(x + y,z) = (x,z) + (y,z);
(ах, у) = а(х, у);
(х, х) ≥ 0, причем равенство (х, х) = 0 возможно лишь в случае, если х = θ.

Пример:

В координатном пространстве Сn, элементами которого являются всевозможные упорядоченные наборы п комплексных чисел, скалярное произведение можно ввести так

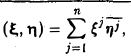
Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Источник