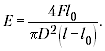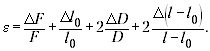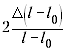Построение графиков и определение погрешностей по ним
Во многих лабораторных работах оказывается, удобным изображать графически зависимость между изучаемыми величинами. Для того, чтобы построить график, необходимо на основании проделанных измерений составить таблицу, в которой каждому значению одной из величин соответствует определенное значение другой. Для правильного построения графика весьма важным является целесообразный выбор масштаба. Масштаб по каждой оси может быть свой, причем выбирать его следует так, чтобы пределы изменений обеих величин ограничивали на осях отрезки примерно одинаковые по величине, иначе график может оказаться очень сжатым по одной из осей и неудобным для пользования. Если первое значение измеряемой величины сильно отличается от нуля и, особенно, если изменение этой величины невелико, отсчет в начале координат нужно начинать не от нуля, а от какого-то значения, близкого к первому измеренному значению данной величины. Когда масштаб выбран, нужно разделить оси в выбранном масштабе на равные интервалы и надписать на осях значения этих интервалов (рис. 1). После этого на график наносят точки на основании данных таблицы и проводят через них прямую или плавную кривую линию.
Так как все измерения сделаны с той или иной ошибкой, то может иметь место некоторый разброс точек (они не укладываются точно на одной кривой). В этом случае линию нужно проводить между точками так, чтобы возможно большее число точек легло на эту линию, а остальные распреде
лились примерно равномерно выше и ниже ее (рис. 1). С помощью полученного графика можно для любого промежуточного значения одной из величин найти соответствующее ему значение другой величины.
Если при построении графика наблюдается значительный разброс точек, то погрешность можно определить сле дующим образом. Нужно измерить отклонение каждой экспериментальной точки от линии графика по направлению, параллельному той оси, вдоль которой отложена интересующая нас величина, и найти среднее значение этого отклонения. В качестве примера рассмотрим вычисление погрешности по графику, изображенному на рис. 1.
Рис.1
На этом графике представлена зависимость оптической плотности раствора от концентрации. Для того, чтобы с помощью этого графика найти погрешность в определении концентрации, нужно измерить в масштабе все значения ∆С, затем сложить их и разделить на число точек:
Такой способ нахождения погрешности удобен при наличии значительного разброса точек. Если же разброс точек невелик, что можно использовать другой способ определения погрешности по графику. На основании графика можно найти абсолютную ошибку в определении одной величины, если известна абсолютная ошибка в определении другой величины. Пусть график изображает зависимость величины у от величины х. Если какое-то значение величины х измерено с ошибкой ∆х, то надо на соответ ствующей оси около этого значения х отложить отрезок ∆х в выбранном масштабе и по графику найти соответствующий ему отрезок ∆у на другой оси. Найденный отрезок ∆у и будет представлять собой абсолютную ошибку в определении интересующего нас значения величины у. В случае прямолинейного графика ошибка, определенная таким образом, во всех его точках одинакова. Если же график представляет собой кривую линию, то ошибка на разных его участках будет различной.
Рис.2
По графику находят значение концентрации, соответствующее среднему значению оптической плотности Dхср. В нашем случае Сх равно 1,42%. Около значения Dхср на оси ординат откладывают отрезок, равный ∆Dхср и по графику находят, какой отрезок соответствует ему на другой оси. Этот отрезок и даст среднюю абсолютную ошибку в опреределении искомой концентрации. Как видно из рис. 2, ∆Сх равно 0,02. Тогда окончательный результат запишется так:
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
Источник
Графическое определение погрешностей
Если изучается зависимость одной величины от другой, то результаты могут быть представлены в виде графика.
Основное достоинство графиков – их наглядность. Посмотрев на график, можно сразу, одним взглядом, охватить вид полученной зависимости, получить о ней качественное представление и отметить наличие различных особенностей: максимумов и минимумов, областей возрастания и убывания, периодичности и т.п. График позволяет также судить о соответствии экспериментальных данных той или иной теоретической зависимости.
При вычерчивании графика в прямоугольной системе координат необходимо руководствоваться следующими правилами.
1. Выбор бумаги. График должен выполнятся на миллиметровой или хотя бы клетчатой бумаге.
2. Выбор координатных осей. По горизонтальной оси принято откладывать ту величину, изменения которой являются причиной изменения другой (т.е. по оси абсцисс – аргумент Х, по оси ординат – функцию Y). На осях координат следует указать название или символ величины и указать, в каких единицах она измеряется:

3. Выбор интервала. На графике приводится только та область изменения измеряемых величин, которая была исследована на опыте, поэтому пересечение координатных осей не обязательно должно совпадать с нулевыми значениями Х = 0 и Y = 0. Например:
4. Выбор масштаба. Масштабы на каждой оси выбираются независимо друг от друга, причем так, чтобы экспериментальные точки не сливались друг с другом и чтобы наилучшим образом использовалась площадь бумаги. Следует помнить, что график получается более наглядным, если основная часть кривой имеет наклон, не слишком отличающийся от 45º.
5. Нанесение шкал по осям. Масштаб наносится на осях графика в виде равностоящих “круглых” чисел, например:
Не следует расставлять эти числа слишком густо – достаточно нанести их через 2 или даже через 5 делений:

6. Нанесение точек на график. На график наносят все полученные в измерениях значения. Если одна точка измерялась несколько раз, можно нанести среднее и указать погрешность. Координаты экспериментальных точек на осях выписывать не нужно, т.к. это загромождает график и мешает его чтению (на осях наносятся только масштабные деления).
Выносные линии на графике, как правило, не проводятся: научитесь наносить точки на график без их помощи. Выносная линия может в виде исключения быть нанесена, только если какую-либо точку хотят особо выделить на графике.
Размечать масштабные деления на осях координат и наносить на график точки лучше всего сначала карандашом. Вдруг вы решите изменить масштаб или окажется, что какая-то точка случайно поставлена неправильно. Если же с масштабом и расположением точек все в порядке, нетрудно обвести все чернилами. В результате же удается избежать переделок и лишних затрат графической бумаги.
7. Проведение кривой по нанесенным точкам. Так как все измерения сделаны с той или иной погрешностью, то может наблюдаться некоторый разброс точек. Нельзя соединять эти точки простой ломаной линией, проходящей через каждую точку, т.к. это означало бы, что зависимость между двумя величинами носит скачкообразный характер, а это маловероятно. Скорее следует ожидать, что данная зависимость описывается какой-либо плавной кривой. Помните, что всякая особенность на кривой (излом, резкое изменение кривизны и т.д.) требует специального экспериментального доказательства, либо теоретического объяснения. Поэтому чаще всего кривую на графике проводят плавно, избегая изломов и перегибов, причем так, чтобы большее число экспериментальных точек легло на эту линию, а остальные равномерно распределились выше и ниже ее.
8. Выбор наиболее наглядной зависимости. При построении графика нужно стремиться к тому, чтобы он наиболее четко отображал все особенности представляемой зависимости. Для этого часто бывают удобны функциональные масштабы – по осям откладываются не сами измеряемые величины, а их функции, подобранные в соответствии с решаемой задачей. Например, если измеряемая величина изменяется очень сильно, на несколько порядков, удобно применять логарифмический (по осям откладываются логарифмы измеряемых величин) или полулогарифмический масштаб (логарифм откладывается только по одной из осей). С примером полулогарифмической шкалы Вы встретитесь в работе по снятию аудиограммы и частотной характеристики импеданса биологической ткани.
При пользовании функциональных масштабов на оси следует наносить двойную шкалу: одну – равномерную для откладываемой по оси функции (например, lg x), а другую – неравномерную для самой величины (но и на эту шкалу наносят, как обычно, “круглые” числа.

9. Оформление графиков. Готовый график, снабжается подписью, которая должна содержать точное описание того, что показывает график.
Ниже показан пример построения графика (к лаб. раб.№ 1).
Рис. 1
Зависимость чувствительности α весов от величины нагрузки P.
10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх =75 г : α 75 = 
11. На основании графика можно найти абсолютную погрешность в определении одной из величин, если известна абсолютная погрешность другой величины. Пусть график изображает зависимость y = f(x) и известно, что некоторое значение величины Х измерено с погрешностью Δх (точка Х0). Тогда
Рис. 2
Зависимость y=f(x)
на графике откладывают на соответствующей оси около значения Х0 величину ΔX в выбранном масштабе и по графику находит соответствующую ей величину отрезка ΔY (см. рис.). Найденное ΔY и будет представлять собой абсолютную погрешность в определении Y.
Источник
Как определить погрешность по графику
Во многих лабораторных работах оказывается, удобным изображать графически зависимость между изучаемыми величинами. Для того, чтобы построить график, необходимо на основании проделанных измерений составить таблицу, в которой каждому значению одной из величин соответствует определенное значение другой. Для правильного построения графика весьма важным является целесообразный выбор масштаба. Масштаб по каждой оси может быть свой, причем выбирать его следует так, чтобы пределы изменений обеих величин ограничивали на осях отрезки примерно одинаковые по величине, иначе график может оказаться очень сжатым по одной из осей и неудобным для пользования. Если первое значение измеряемой величины сильно отличается от нуля и, особенно, если изменение этой величины невелико, отсчет в начале координат нужно начинать не от нуля, а от какого-то значения, близкого к первому измеренному значению данной величины. Когда масштаб выбран, нужно разделить оси в выбранном масштабе на равные интервалы и надписать на осях значения этих интервалов (рис. 1). После этого на график наносят точки на основании данных таблицы и проводят через них прямую или плавную кривую линию.
Так как все измерения сделаны с той или иной ошибкой, то может иметь место некоторый разброс точек (они не укладываются точно на одной кривой). В этом случае линию нужно проводить между точками так, чтобы возможно большее число точек легло на эту линию, а остальные распреде
лились примерно равномерно выше и ниже ее (рис. 1). С помощью полученного графика можно для любого промежуточного значения одной из величин найти соответствующее ему значение другой величины.
Если при построении графика наблюдается значительный разброс точек, то погрешность можно определить сле дующим образом. Нужно измерить отклонение каждой экспериментальной точки от линии графика по направлению, параллельному той оси, вдоль которой отложена интересующая нас величина, и найти среднее значение этого отклонения. В качестве примера рассмотрим вычисление погрешности по графику, изображенному на рис. 1.
Рис.1
На этом графике представлена зависимость оптической плотности раствора от концентрации. Для того, чтобы с помощью этого графика найти погрешность в определении концентрации, нужно измерить в масштабе все значения ∆С, затем сложить их и разделить на число точек:
Такой способ нахождения погрешности удобен при наличии значительного разброса точек. Если же разброс точек невелик, что можно использовать другой способ определения погрешности по графику. На основании графика можно найти абсолютную ошибку в определении одной величины, если известна абсолютная ошибка в определении другой величины. Пусть график изображает зависимость величины у от величины х. Если какое-то значение величины х измерено с ошибкой ∆х, то надо на соответ ствующей оси около этого значения х отложить отрезок ∆х в выбранном масштабе и по графику найти соответствующий ему отрезок ∆у на другой оси. Найденный отрезок ∆у и будет представлять собой абсолютную ошибку в определении интересующего нас значения величины у. В случае прямолинейного графика ошибка, определенная таким образом, во всех его точках одинакова. Если же график представляет собой кривую линию, то ошибка на разных его участках будет различной.
Рис.2
По графику находят значение концентрации, соответствующее среднему значению оптической плотности Dхср. В нашем случае Сх равно 1,42%. Около значения Dхср на оси ординат откладывают отрезок, равный ∆Dхср и по графику находят, какой отрезок соответствует ему на другой оси. Этот отрезок и даст среднюю абсолютную ошибку в опреределении искомой концентрации. Как видно из рис. 2, ∆Сх равно 0,02. Тогда окончательный результат запишется так:
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Если изучается зависимость одной величины от другой, то результаты могут быть представлены в виде графика.
Основное достоинство графиков – их наглядность. Посмотрев на график, можно сразу, одним взглядом, охватить вид полученной зависимости, получить о ней качественное представление и отметить наличие различных особенностей: максимумов и минимумов, областей возрастания и убывания, периодичности и т.п. График позволяет также судить о соответствии экспериментальных данных той или иной теоретической зависимости.
При вычерчивании графика в прямоугольной системе координат необходимо руководствоваться следующими правилами.
1. Выбор бумаги. График должен выполнятся на миллиметровой или хотя бы клетчатой бумаге.
2. Выбор координатных осей. По горизонтальной оси принято откладывать ту величину, изменения которой являются причиной изменения другой (т.е. по оси абсцисс – аргумент Х, по оси ординат – функцию Y). На осях координат следует указать название или символ величины и указать, в каких единицах она измеряется:

3. Выбор интервала. На графике приводится только та область изменения измеряемых величин, которая была исследована на опыте, поэтому пересечение координатных осей не обязательно должно совпадать с нулевыми значениями Х = 0 и Y = 0. Например:
4. Выбор масштаба. Масштабы на каждой оси выбираются независимо друг от друга, причем так, чтобы экспериментальные точки не сливались друг с другом и чтобы наилучшим образом использовалась площадь бумаги. Следует помнить, что график получается более наглядным, если основная часть кривой имеет наклон, не слишком отличающийся от 45º.
5. Нанесение шкал по осям. Масштаб наносится на осях графика в виде равностоящих “круглых” чисел, например:
Не следует расставлять эти числа слишком густо – достаточно нанести их через 2 или даже через 5 делений:

6. Нанесение точек на график. На график наносят все полученные в измерениях значения. Если одна точка измерялась несколько раз, можно нанести среднее и указать погрешность. Координаты экспериментальных точек на осях выписывать не нужно, т.к. это загромождает график и мешает его чтению (на осях наносятся только масштабные деления).
Выносные линии на графике, как правило, не проводятся: научитесь наносить точки на график без их помощи. Выносная линия может в виде исключения быть нанесена, только если какую-либо точку хотят особо выделить на графике.
Размечать масштабные деления на осях координат и наносить на график точки лучше всего сначала карандашом. Вдруг вы решите изменить масштаб или окажется, что какая-то точка случайно поставлена неправильно. Если же с масштабом и расположением точек все в порядке, нетрудно обвести все чернилами. В результате же удается избежать переделок и лишних затрат графической бумаги.
7. Проведение кривой по нанесенным точкам. Так как все измерения сделаны с той или иной погрешностью, то может наблюдаться некоторый разброс точек. Нельзя соединять эти точки простой ломаной линией, проходящей через каждую точку, т.к. это означало бы, что зависимость между двумя величинами носит скачкообразный характер, а это маловероятно. Скорее следует ожидать, что данная зависимость описывается какой-либо плавной кривой. Помните, что всякая особенность на кривой (излом, резкое изменение кривизны и т.д.) требует специального экспериментального доказательства, либо теоретического объяснения. Поэтому чаще всего кривую на графике проводят плавно, избегая изломов и перегибов, причем так, чтобы большее число экспериментальных точек легло на эту линию, а остальные равномерно распределились выше и ниже ее.
Во всех случаях кривая должна быть проведена так, чтобы она не закрывала экспериментальных точек. Помните, что результат эксперимента — это точки, а кривая – это только Ваше толкование результата (вообще говоря, не однозначное).
8. Выбор наиболее наглядной зависимости. При построении графика нужно стремиться к тому, чтобы он наиболее четко отображал все особенности представляемой зависимости. Для этого часто бывают удобны функциональные масштабы – по осям откладываются не сами измеряемые величины, а их функции, подобранные в соответствии с решаемой задачей. Например, если измеряемая величина изменяется очень сильно, на несколько порядков, удобно применять логарифмический (по осям откладываются логарифмы измеряемых величин) или полулогарифмический масштаб (логарифм откладывается только по одной из осей). С примером полулогарифмической шкалы Вы встретитесь в работе по снятию аудиограммы и частотной характеристики импеданса биологической ткани.
При пользовании функциональных масштабов на оси следует наносить двойную шкалу: одну – равномерную для откладываемой по оси функции (например, lg x), а другую – неравномерную для самой величины (но и на эту шкалу наносят, как обычно, “круглые” числа.

9. Оформление графиков. Готовый график, снабжается подписью, которая должна содержать точное описание того, что показывает график.
Ниже показан пример построения графика (к лаб. раб.№ 1).
Рис. 1
Зависимость чувствительности α весов от величины нагрузки P.
10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх =75 г : α 75 = 
11. На основании графика можно найти абсолютную погрешность в определении одной из величин, если известна абсолютная погрешность другой величины. Пусть график изображает зависимость y = f(x) и известно, что некоторое значение величины Х измерено с погрешностью Δх (точка Х0). Тогда
Рис. 2
Зависимость y=f(x)
на графике откладывают на соответствующей оси около значения Х0 величину ΔX в выбранном масштабе и по графику находит соответствующую ей величину отрезка ΔY (см. рис.). Найденное ΔY и будет представлять собой абсолютную погрешность в определении Y.
Гальванопластика — направление прикладной электрохимии, направленное на создание изделий путем электрохимического осаждения металлов и сплавов на различные носители формы (формообразующие элементы) в жидких средах.
Принцип формирования металлического осадка на поверхности модели, такой же как и при гальваническом нанесении покрытий, но в отличии от классической гальваники (гальваностегии) – толщина формируемых металлических осадков может достигать нескольких сантиметров.
В первой половине 20 века применение гальванопластики с целью получения технических изделий превратилось в полноценную промышленную технологию получения сложных и точных изделий.
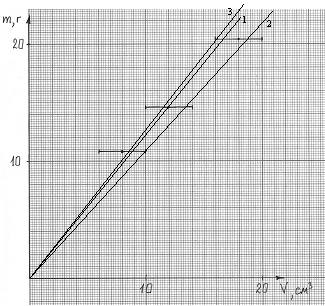
При построении калибровочной прямой методом наименьших квадратов считается, что стандарты для калибровки известны с абсолютной правильностью или по крайней мере погрешности стандартов на одной из осей координат несущественны по сравнению с погрешностями откликов прибора на другой оси. Каждый отсчёт показаний шкалы прибора является единичным наблюдением, взятым из генеральной совокупности всех возможных отсчётов показаний шкалы прибора, при введении в него данного химического вещества. Такая ситуация изображена на рисунке:
Небольшие кривые нормального распределения, начерченные на графике, представляют генеральную совокупность всех возможных сигналов прибора при измерении стандартов 0,300, 0,600, 0,900 мг/дм3. Точка А, наблюдаемая в процессе калибровки, расположена близко к центру этого распределения (в пределах ±2σ, обозначенных штрихами). В данной ситуации точка А, представляющая значение оптической плотности стандарта 0,300 мг/л, находится близко к генеральному среднему. Но при измерении необходимо, чтобы калибровочная прямая проходила не через точку А, а точно через центр распределения, который обозначен стрелкой, для чего мы пользовались методом наименьших квадратов. Для минимизации погрешности относительно оси У при составлении градуировочного графика используются средние значения трёх параллельных измерений каждого стандартного образца (см. «Статистическая обработка данных титриметрического анализа»), поэтому эти расчёты мы рассматривать не будем. Мы рассмотрим расчёт доверительных интервалов для коэффициента bи полученной в ходе измерения концентрации вещества в исследуемом растворе xk.
При определении недостоверностей при работе методом градуировочного графика первая необходимая величина, надлежащая определению, — дисперсия, обусловленная рассеянием точек относительно линии регрессии, выраженная уравнением:
Далее определяется дисперсия коэффициента регрессии или стандартного отклонения b:
Доверительные интервалы задаются обычным способом по таблице коэффициентов Стьюдента при доверительной вероятности 95%:
за тем исключением, что число степеней свободы k = n-2, где n– количество стандартов для градуировки.
На практике линию регрессии (линию градуировочного графика) используются, чтобы получить оценку некоторой величины (в нашем случае концентрации железа II) xk измеряемого вещества, которая вызывает наблюдаемый отклик прибора yk (поглощение раствора). Дисперсия определяемой величины xk при наблюдении mоткликов (m – количество параллельных измерений) выражается уравнением:
а) xk – характеристика вещества, ответственного за отклик прибора. В нашем случае xk – концентрация железа II, соответствующая наблюдаемому поглощению раствора yk.
б) yk(∑yk/m) – средний отклик прибора, полученный для ряда из mизмерений. Часто проводят только одно измерение и поэтому m=1.
в) Величины s 2 x,y, b, n, у¯ и ∑U 2 связаны с данными при калибровке прибора и имеют те же самые значения, что мы получили при уточнении градуировочного графика методом наименьшик квадратов.
Стоит обратить особое внимание, что s 2 xkвозрастает по мере удаления yk от у¯. Из математического выражения следует, что недостоверность любой оценки регрессии меньше всего вероятна вблизи центра калибровочных данных и поэтому экстраполяция представляет собой очень ненадёжный метод и при измерениях не используется. Разбавление исследуемого раствора подбирается таким образом, чтобы отклик прибора при измерении попадал как можно ближе к центру градуировочной прямой.
Доверительные интервалы для определяемой величины xk выражаются следующим образом:
Продолжим расчёт определения железа IIпо градуировочному графику, построенному по 6 точкам (n=6) с уравнением регрессии у = 0,002245098 + 10914,70588х (см. Применение регрессионного анализа для построения градуировочного графика при фотометрическом анализе).
Допустим, что а) при единичном (m=1) измерении исследуемого раствора получено поглощение равное 0,527, б) при пяти (m=5) повторных измерениях среднее поглощение равно 0,527.
1) Вычисляем дисперсию относительно линии регрессии:
s 2 x,y = (∑V 2 – b 2 ∑U 2 )/(n-2) = (0,40539683 – (10914,70588^2)*0,0000000034)/(6-2) = 0,0000880245098
2) Вычисляем стандартное отклонение b:
s 2 bx,y = s 2 x,y / ∑U 2 = 0,0000880245098 / 0,0000000034 = 25889,561707
3) Рассчитываем доверительный интервал для коэффициента b:
При доверительной вероятности 95% для φ=n-2=4 коэффициент tα,φ принимает значение 2,776 (см. таблицу коэффициентов Стьюдента).
b = (10914,70588 ± 446,66) ≈ (10915 ± 447)
4) Рассчитаем по уравнению регрессии, выразив его через x, концентрацию железа IIxkпо поглощению 0,527, полученному в ходе измерения исследуемого раствора:
5) Стандартное отклонение оценки регрессии s 2 xk для случаев а) m=1 и б) m=5:
а) s 2 xk = (s 2 x,y / b 2 ) * [(1/m + 1/n) + (у¯k — у¯) 2 / b 2 ∑U 2 )] = (0,0000880245098 / 10914,70588^2)*[(1/1 + 1/6) + (0,527 — 0,438833)^2 / (10914,70588^2 * 0,0000000034] = 0,000000000000876218
sxk = √s 2 xk = √0,000000000000876218 = 0,000000936065
б) s 2 xk = (0,0000880245098 / 10914,70588^2)*[(1/5 + 1/6) + (0,527 — 0,438833)^2 / (10914,70588^2 * 0,0000000034] = 0,0000000000002851065
sxk = √0,0000000000002851065 = 0,0000005339536
6) Рассчитываем доверительный интервал для xk:
При доверительной вероятности 95% для φ=n-2=4 коэффициент tα,φ принимает значение 2,776 (см. таблицу коэффициентов Стьюдента).
а) ДИ = ε α,t =±tα, φ * sxk = 2,776* 0,000000936065 = 0,000002598
xk = (0,00004807778 ± 0,000002598) ≈ (0,0000481 ± 0,0000026) моль/л
б) ДИ = ε α,t = ±tα, φ * sxk = 2,776*0,0000005339536 = 0,0000014823
xk = (0,00004807778 ± 0,0000014823) ≈ (0,0000481 ± 0,0000015) моль/л
7) Рассчитываем относительную ошибку определения:
а) εотн = (ε α,t / хk)*100 = 0,0000026*100/0,0000481 = 5,4%
б) εотн = (ε α,t / хk)*100 = 0,0000015*100/0,0000481 = 3,1%
Расчёты относительных ошибок измерений показывают, что использование метода наименьших квадратов не может заменить правильность самих калибровочных данных. Метод наименьших квадратов не должен применяться только для расчётов коэффициентов a и b, но должны рассчитываться также недостоверности относительно линии регрессии по алгоритму, указанному выше. При исключении расчётов недостоверностей статистический метод используется неправильно, и химик-аналитик обманывает себя и других, приводя в своих результатах слишком много значащих цифр.
Образец автоматических расчётов недостоверностей градуировочного графика, построенного по 6 точкам, можно скачать здесь .
1. Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение. Теория и практика аналитической химии. – М.: «Химия», 1978. – 816 с.
2. А.П.Крешков. Основы аналитической химии. Книга вторая. — М.: «Химия», 1971.- 456 с.
Источник
19
Суммарная абсолютная погрешность R с доверительной вероятностью (α = 0,96) будет равна в соответствии с формулой (3.10):
q
Δ(R)сум = 122 + (3 · 3,4)2 = 15,7 Ом.
Окончательно, с доверительной вероятностью α = 0,96 можно утверждать, что искомая величина
R = 498 ± 16 Ом.
7.1 Построение графиков с использованием доверительных интервалов
В практике научных исследований очень часто приходится строить графические зависимости одной из измеряемых величин от другой. Наличие погрешностей измерений обусловливает тот факт, что экспериментальные точки не точно ложатся на прямую или кривую, выражающую теоретическую зависимость между этими величинами.
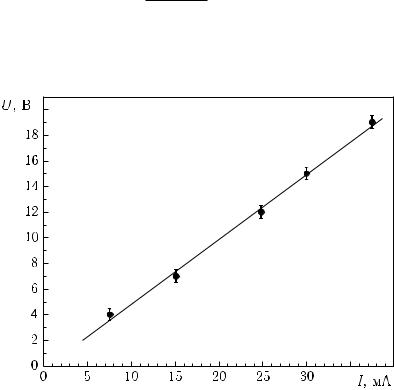
Например, на рисунке 7.1 показана экспериментальная зависимость напряжения на неизвестном сопротивлении R от величины протекающего через него тока. Экспериментальные точки расположились так, что однозначно провести прямую, выражающую эту зависимость, затруднительно: на рисунке 7.1 показаны три возможных варианта зависимости. Какой из них верен?
Рисунок 7.1 – Зависимость напряжения U на сопротивлении от тока I
20
Один из широко распространенных приближенных методов проведения экспериментальной зависимости заключается в том, что на графике указываются доверительные интервалы значений измеренных величин. При построении доверительного интервала следует иметь в виду две ситуации:
1)каждая экспериментальная точка результат многократного измерения. В этом случае следует найти суммарные абсолютные погрешности каждой из измеренных величин (см. подразделы 3.1 3.3): они откладываются по обе стороны от точки на графике вдоль соответствующих координатных осей. При этом можно точно указать доверительную вероятность проведенных измерений;
2)гораздо чаще встречающийся случай: каждая экспериментальная точка результат однократного измерения. В этом случае можно найти только абсолютные систематические погрешности результатов измерений и также отложить по обе стороны от соответствующей экспериментальной точки. Следует заметить, что для приборов,
укоторых постоянной является абсолютная погрешность (класс точности таких приборов обозначается, например, 1,0), отрезки доверительных интервалов будут одинаковыми; если измерения проведены с помощью изучаемых цифровых приборов, доверительные интервалы будут неодинаковыми.
В качестве примера рассмотрим еще один метод измерения сопротивления, при котором не стараются установить одно и то же значение напряжения, как в разделе 6, а измеряется ток при заведомо разных напряжениях. Каждое из этих измерений проводится один раз. Положим, что приборы имеют те же характеристики, что и в разделе 6. Результаты измерений представлены в таблице 7.1.
Таблица 7.1 – Результаты измерений тока и напряжения
|
I, мА |
7,53 |
15,1 |
24,8 |
30,0 |
37,5 |
|
U , В |
4 |
7 |
12 |
15 |
19 |
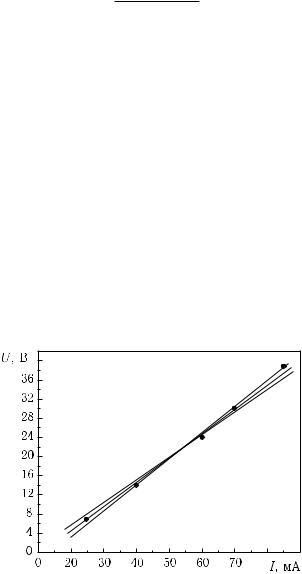
По результатам измерений построен график (рисунок 7.2). Экспериментальные точки не строго укладываются на прямую
и, чтобы провести эту прямую более точно, построим доверительные интервалы. Так как измерения однократные, то доверительные интервалы будут представлять собой абсолютные погрешности приборов, с помощью которых проводились измерения тока и напряжения. При классе точности вольтметра 1,0 и максимальном значении шкалы прибора 50 В абсолютная погрешность равна 0,5 В. Параллельно оси напряжения вверх и вниз от каждой экспериментальной точки надо отложить 0,5 В в масштабе графика (рисунок 7.2).
|
21 |
|||
|
У миллиамперметра абсолютная погрешность изменяется, чем |
|||
|
больше величина тока, тем больше погрешность. Максимальная ве- |
|||
|
личина абсолютной систематической погрешности измерения тока |
|||
|
будет равна: |
|||
|
Δ(I) |
= 1,2% · 37,5 + 1 |
· |
0,1 = 0,6 мА. |
|
сист |
100% |
||
|
В масштабе рисунка 7.2 это соответствует примерно 1 мм. Для |
|||
|
других экспериментальных точек “размер” доверительного интерва- |
|||
|
ла на графике будет еще меньше. Такие малые интервалы на графи- |
|||
|
ках обычно не откладываются. |
|||
|
Рисунок 7.2 – Связь между током I и напряжением U для постоянного |
|||
|
сопротивления |
|||
|
Прямую следует провести так, чтобы она прошла внутри всех до- |
|||
|
верительных интервалов. Во многих случаях оказывается, что про- |
|||
|
вести прямую с соблюдением этого условия возможно единственным |
|||
|
образом. При нахождении какой-либо величины x из графика аб- |
|||
|
солютная погрешность этой величины Δ(x) равна половине цены |
|||
|
деления соответствующей шкалы графика. |
|||
|
Рекомендуется самостоятельно рассчитать сопротивление R и по- |
|||
|
грешность Δ(R) в рассмотренном примере. |

22
7.2Линеаризация функций
Вфизических исследованиях очень часто для сравнения эксперимента с теорией пользуются методом линеаризации теоретической зависимости. Например, исследуется зависимость тока вакуумного диода I от величины задерживающего напряжения U между катодом и анодом. Теоретическая зависимость имеет следующий вид:
|
eU |
, |
|
|
I = I0 exp −kT |
(7.1) |
где I0 ток при U = 0; k постоянная Больцмана; T абсолютная температура; e заряд электрона.
|
Построенная |
по |
экспериментальным данным зависимость |
|
I = f (U ) может |
с |
равным успехом иллюстрировать и квадра- |
тичную, и кубическую, и экспоненциальную зависимости. Чтобы выяснить, подтверждают ли экспериментальные данные теорию, теоретическую зависимость преобразуют так, чтобы между функцией I и аргументом U была линейная зависимость.
|
Прологарифмировав выражение (7.1), получим: |
||||||
|
ln I = ln I0 − |
e |
U. |
(7.2) |
|||
|
kT |
||||||
|
Это уравнение прямой вида: |
||||||
|
y = b − ax, |
(7.3) |
|||||
|
где |
y = ln I; |
b = ln I0; |
a = |
e |
угловой коэффициент |
прямой; |
|
kT |
x = U .
Если экспериментальные результаты улягутся на прямую (в пределах погрешностей измерений) в координатах ln I = f (U )), можно утверждать, что зависимость между I и U носит именно экспоненциальный характер, как это и следует из теории (рисунок 7.3).
Во многих случаях знание углового коэффициента a и величины b позволяет определить и другие параметры изучаемого явления. В данном примере, зная a, можно определить температуру катода.
Страница 1 из 6
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ этой теме буду писать что-то вроде краткой шпаргалки по погрешностям. Опять же, данный текст ни в коей мере не официальный и ссылаться на него недопустимо. Буду признателен за исправление любых ошибок и неточностей, которые могут быть в этом тексте.
Что такое погрешность?
Запись результата эксперимента вида
(
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
, а в 30% — не будут.
Или, что тоже самое, если мы повторим эксперимент, то новый результат ляжет в доверительный интервал
с вероятностью, равной доверительной вероятности
.
Как округлять погрешность и результат?
Погрешность округляется до первой значащей цифры, если она не единица. Если единица — то до двух. При этом значащей цифрой называется любая цифра результата кроме нулей впереди.
Пример:
округляем до
или
или
но ни в коем случае не
или
, поскольку тут 2 значащие цифры — 2 и 0 после двойки.
округляем до
или
округляем до
или
или
Результат округляем таким образом, чтобы последняя значащая цифра результата соответствовала последней значащей цифре погрешности.
Примеры правильной записи:
мм
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица.
мм
Примеры неправильной записи:
мм. Здесь лишний знак в результате. Правильно будет
мм.
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм.
В работе использую значение, данное мне просто в виде цифры. Например, масса грузиков. Какая у нее погрешность?
Если погрешность явно не указана, можно взять единицу в последнем разряде. То есть если написано m=1.35 г, то в качестве погрешность нужно взять 0.01 г.
Как считать погрешность сложной функции?
Есть функция от нескольких величин
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
символ
означает частную производную f по x. Подробнее про частные производные здесь.
Как вообще правильно посчитать погрешность?
Положим, вы меряли одну и ту же величину x несколько (n) раз. Получили набор значений.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
По пунктам.
1. Считаем погрешность разброса
Если все значения совпали — никакого разброса у вас нет. Иначе — есть погрешность разброса
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
здесь
означает среднее по всем
.
Погрешность разбросаполучается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента
, который зависит от выбранной вами доверительной вероятности
и числа измерений n:
.
Коэффициенты Стьюдента
берем из нижеприведенной таблицы. Доверительная вероятность
выбитается произвольно, число измерений n мы также знаем.
2. Считаем приборную погрешность среднего
Если погрешности разных точек разные, то по формуле
При этом естественно, у всех
доверительная вероятность должна быть одинаковой.
3. Складываем среднее с разбросом
Погрешности всегда складываются как корень из квадратов:
При этом нужно убедиться, что доверительные вероятности с которыми были вычислены
и
совпадают.
Как по графику определить приборную погрешность среднего? Ну т.е., используя метод парных точек или метод наименьших квадратов, мы найдем погрешность разброса среднего сопротивления. Как найти приборную погрешность среднего сопротивления?
И в МНК и в методе парных точек можно дать строгий ответ на этот вопрос. Для МНК форума в Светозарове есть («Основы…», раздел про метод наименьших квадратов), а для парных точек первое, что приходит в голову (в лоб, что называется) это посчитать приборную погрешность каждого углового коэффициента. Ну и далее по всем пунктам…
Если же не хочешь мучиться, то в лабниках дан простой способ для оценки приборной погрешности углового коэффициента, именно из МНК следующий (например перед работой 1 в лабнике «Электроизмерительные приборы. …» последняя страница Метод.рекомендаций).
, где
— величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
На магазине сопротивлений написан класс точности: 0,05/4*10^-6? Как из этого найти погрешность прибора?Это означает, что предельная относительная погрешность прибора (в процентах) имеет вид:
, где
— наибольшее значение сопротивления магазина, а
— номинальное значение включённого сопротивления.
Легко видеть, что второе слагаемое важно тогда, когда мы работаем на очень малых сопротивлениях.Подробнее всегда можно посмотреть в паспорте прибора. Паспорт можно найти в интернете, забив марку прибора в гугл.
Литература про погрешности
Рецептурная информация про то как считать погрешности дана во введениях к практикумам, в частности, во вводной части к практикуму «Измерительные приборы».
Гораздо больше информации по этому поводу можно найти в рекомендованной для первокурсников книге:
В.В. Светозаров «Элементарная обработка результатов измерений»В качестве дополнительной (для первокурсников дополнительной) литературы можно порекомендовать:
В.В.Светозаров «Основы статистической обработки результатов измерений»И уж тем кто хочет окончательно во всем разобраться непременно стоит заглянуть сюда:
Дж. Тейлор. «Введение в теорию ошибок»Спасибо Lexxus’у за нахождение и размещение у себя на сайте этих замечательных книжек.
-
Lexxus
Немного великий
Администратор
VIPА разве не
? -
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторНеа. Последняя значащая цифра результата должна отвечать последней значащей цифре погрешности.
Если мы держим миллиметры в погрешности, то почему их надо убирать в результате? -
0,98 можно округлить так:
?
-
Lexxus
Немного великий
Администратор
VIP[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:?
[/quote]
0.98 можно округлять до 1.0, если погрешность получилась 0.195 и более.
В противном случае, округлять до 1.0 нельзя. -
Lexxus
Немного великий
Администратор
VIPlamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность — скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае — до десятков), т.е. записать?
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:?
[/quote]0,98 это результат или погрешность?
[quote name=’Lexxus’ post=’379428′ date=’Oct 5 2010, 16:53′]
lamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность — скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае — до десятков), т.е. записать?
[/quote]
Да, именно так, если я правильно понимаю. Связано, как я понимаю, с тем, что погрешность округления самой погрешности в этом случае превысит результат.
То есть я понимаю, что четверка несет в себе некую информацию, которая убивается округлением. Но по сравнению с самой погрешностью, и с ее ошибкой округления, это уже все мало.
-
А в чем разница 2х примеров? Во втором случае оба числа просто на порядок меньше. Нельзя их записать как-то типа
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ первом случае первая цифра в погрешности — единица. Из-за этого мы держим в погрешности 2 знака, чтобы минимизировать ошибку округления погрешности. Во втором — четверка. И мы оставляем только один знак.
-
Т.е.
— правильно?
Думаю, тогда стоит в инструкции более ясно написать, почему предыдущее не правильно.
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторДа. А +- 4.2 — неправильно.Предлагай. У меня-то глаз замылен, мне все кажется понятным
.
-
результат
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379443′ date=’Oct 5 2010, 17:41′]
результат
[/quote]
Тогда тебе Lexxus ответил.[quote name=’Chameleon’ post=’379445′ date=’Oct 5 2010, 17:42′]
как так «завернуто»
[/quote]Слишком сложно для восприятия, имхо. Смешано в кучу правильное и неправильное. Я чуть выше, в примерах правильной записи, добавил строчку, поясняющую различие. И, кстати, про единицу сказано выше.
-
т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор -
[quote name=’Silver MC’s’ date=’Oct 5 2010, 18:19′]
[snapback]379453[/snapback]т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9[/quote]
Нет. Если погрешность 0,1, то дадо писать так: $0.98pm0.10
Если в погрешности 1я значащая цифра 1, то второй знак обязателен.
PS Если преподаватели немного посвирепствуют, то никакие мануалы и не нужны. Кстати в Светозарове то же самое написано, что и тут. -
Мне кажется, стоит еще написать:
1. как округлять пятерку в последнем разряде (у преподавателей разных кафедр похоже требования разные)
1.56
1.54
1.55
1.52. на пальцах объяснить что значит частная производная с простеньким примерчиком
Если надо — текст попозже напишу
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторNick_, а надо ли тут так вдаваться в математику? тем более в элементарную, вроде правил округления?
-
Lexxus
Немного великий
Администратор
VIPПроблема в том, что функции многих переменных и частные производные в курсе матанализа, кажется, где-то ближе к концу первого семестра.
Страница 1 из 6
Поделиться этой страницей

- Access. Базы данных. Определение ключей и составление запросов.
- B3.4. Правила оформления графиков
- I. Дифракция Фраунгофера на одной щели и определение ширины щели.
- I. Определение
- I. Определение
- I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
- I. Определение пероксида водорода (перекиси водорода)
- I. Определение проблемы и целей исследования
- I. Определение ранга матрицы
- I. Пограничное состояние у новорожденных детей. Определение, характеристика, тактика медицинского работника.
- I. Сестринский процесс при гипертонической болезни: определение, этиология, клиника. Принципы лечения и уход за пациентами, профилактика.
- I. Сестринский процесс при диффузном токсическом зобе: определение, этиология, патогенез, клиника. Принципы лечения и ухода за пациентами
Во многих лабораторных работах оказывается, удобным изображать графически зависимость между изучаемыми величинами. Для того, чтобы построить график, необходимо на основании проделанных измерений составить таблицу, в которой каждому значению одной из величин соответствует определенное значение другой. Для правильного построения графика весьма важным является целесообразный выбор масштаба. Масштаб по каждой оси может быть свой, причем выбирать его следует так, чтобы пределы изменений обеих величин ограничивали на осях отрезки примерно одинаковые по величине, иначе график может оказаться очень сжатым по одной из осей и неудобным для пользования. Если первое значение измеряемой величины сильно отличается от нуля и, особенно, если изменение этой величины невелико, отсчет в начале координат нужно начинать не от нуля, а от какого-то значения, близкого к первому измеренному значению данной величины. Когда масштаб выбран, нужно разделить оси в выбранном масштабе на равные интервалы и надписать на осях значения этих интервалов (рис. 1). После этого на график наносят точки на основании данных таблицы и проводят через них прямую или плавную кривую линию.
Так как все измерения сделаны с той или иной ошибкой, то может иметь место некоторый разброс точек (они не укладываются точно на одной кривой). В этом случае линию нужно проводить между точками так, чтобы возможно большее число точек легло на эту линию, а остальные распреде
лились примерно равномерно выше и ниже ее (рис. 1). С помощью полученного графика можно для любого промежуточного значения одной из величин найти соответствующее ему значение другой величины.
Если при построении графика наблюдается значительный разброс точек, то погрешность можно определить сле дующим образом. Нужно измерить отклонение каждой экспериментальной точки от линии графика по направлению, параллельному той оси, вдоль которой отложена интересующая нас величина, и найти среднее значение этого отклонения. В качестве примера рассмотрим вычисление погрешности по графику, изображенному на рис. 1.
Рис.1
На этом графике представлена зависимость оптической плотности раствора от концентрации. Для того, чтобы с помощью этого графика найти погрешность в определении концентрации, нужно измерить в масштабе все значения ∆С, затем сложить их и разделить на число точек:
Такой способ нахождения погрешности удобен при наличии значительного разброса точек. Если же разброс точек невелик, что можно использовать другой способ определения погрешности по графику. На основании графика можно найти абсолютную ошибку в определении одной величины, если известна абсолютная ошибка в определении другой величины. Пусть график изображает зависимость величины у от величины х. Если какое-то значение величины х измерено с ошибкой ∆х, то надо на соответ ствующей оси около этого значения х отложить отрезок ∆х в выбранном масштабе и по графику найти соответствующий ему отрезок ∆у на другой оси. Найденный отрезок ∆у и будет представлять собой абсолютную ошибку в определении интересующего нас значения величины у. В случае прямолинейного графика ошибка, определенная таким образом, во всех его точках одинакова. Если же график представляет собой кривую линию, то ошибка на разных его участках будет различной.
В качестве примера графического вычисления ошибки разберем определение концентрации окрашенного раствора по величине его оптической плотности. В этой работе сначала измеряется оптическая плотность D нескольких растворов с известной концентрацией С и на основании этих данных строится график зависимости оптической плотности от концентрации (рис. 2). Затем измеряется величина оптической плотности Dх раствора неизвестной концентрации. Пусть, она была измерена 3 раза и оказалась равной: 0,76, 0,78 и 0,75. Тогда среднее значение Dхср = 0,76, а средняя абсолютная ошибка ∆Dхср = 0 ,0 1.
Рис.2
По графику находят значение концентрации, соответствующее среднему значению оптической плотности Dхср. В нашем случае Сх равно 1,42%. Около значения Dхср на оси ординат откладывают отрезок, равный ∆Dхср и по графику находят, какой отрезок соответствует ему на другой оси. Этот отрезок и даст среднюю абсолютную ошибку в опреределении искомой концентрации. Как видно из рис. 2, ∆Сх равно 0,02. Тогда окончательный результат запишется так:
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Если изучается зависимость одной величины от другой, то результаты могут быть представлены в виде графика.
Основное достоинство графиков – их наглядность. Посмотрев на график, можно сразу, одним взглядом, охватить вид полученной зависимости, получить о ней качественное представление и отметить наличие различных особенностей: максимумов и минимумов, областей возрастания и убывания, периодичности и т.п. График позволяет также судить о соответствии экспериментальных данных той или иной теоретической зависимости.
При вычерчивании графика в прямоугольной системе координат необходимо руководствоваться следующими правилами.
1. Выбор бумаги. График должен выполнятся на миллиметровой или хотя бы клетчатой бумаге.
2. Выбор координатных осей. По горизонтальной оси принято откладывать ту величину, изменения которой являются причиной изменения другой (т.е. по оси абсцисс – аргумент Х, по оси ординат – функцию Y). На осях координат следует указать название или символ величины и указать, в каких единицах она измеряется:

3. Выбор интервала. На графике приводится только та область изменения измеряемых величин, которая была исследована на опыте, поэтому пересечение координатных осей не обязательно должно совпадать с нулевыми значениями Х = 0 и Y = 0. Например:
4. Выбор масштаба. Масштабы на каждой оси выбираются независимо друг от друга, причем так, чтобы экспериментальные точки не сливались друг с другом и чтобы наилучшим образом использовалась площадь бумаги. Следует помнить, что график получается более наглядным, если основная часть кривой имеет наклон, не слишком отличающийся от 45º.
Масштаб должен быть простым и легко читаться, поэтому одна клетка масштабной сетки должна соответствовать удобному числу – 1, 2, 5, 10 … , 0,1, 0,2, 0,5, (но не 3, 7, 11, 13 …), единиц изображаемой на графике величины.
5. Нанесение шкал по осям. Масштаб наносится на осях графика в виде равностоящих “круглых” чисел, например:
Не следует расставлять эти числа слишком густо – достаточно нанести их через 2 или даже через 5 делений:

6. Нанесение точек на график. На график наносят все полученные в измерениях значения. Если одна точка измерялась несколько раз, можно нанести среднее и указать погрешность. Координаты экспериментальных точек на осях выписывать не нужно, т.к. это загромождает график и мешает его чтению (на осях наносятся только масштабные деления).
Выносные линии на графике, как правило, не проводятся: научитесь наносить точки на график без их помощи. Выносная линия может в виде исключения быть нанесена, только если какую-либо точку хотят особо выделить на графике.
Размечать масштабные деления на осях координат и наносить на график точки лучше всего сначала карандашом. Вдруг вы решите изменить масштаб или окажется, что какая-то точка случайно поставлена неправильно. Если же с масштабом и расположением точек все в порядке, нетрудно обвести все чернилами. В результате же удается избежать переделок и лишних затрат графической бумаги.
7. Проведение кривой по нанесенным точкам. Так как все измерения сделаны с той или иной погрешностью, то может наблюдаться некоторый разброс точек. Нельзя соединять эти точки простой ломаной линией, проходящей через каждую точку, т.к. это означало бы, что зависимость между двумя величинами носит скачкообразный характер, а это маловероятно. Скорее следует ожидать, что данная зависимость описывается какой-либо плавной кривой. Помните, что всякая особенность на кривой (излом, резкое изменение кривизны и т.д.) требует специального экспериментального доказательства, либо теоретического объяснения. Поэтому чаще всего кривую на графике проводят плавно, избегая изломов и перегибов, причем так, чтобы большее число экспериментальных точек легло на эту линию, а остальные равномерно распределились выше и ниже ее.
Во всех случаях кривая должна быть проведена так, чтобы она не закрывала экспериментальных точек. Помните, что результат эксперимента — это точки, а кривая – это только Ваше толкование результата (вообще говоря, не однозначное).
8. Выбор наиболее наглядной зависимости. При построении графика нужно стремиться к тому, чтобы он наиболее четко отображал все особенности представляемой зависимости. Для этого часто бывают удобны функциональные масштабы – по осям откладываются не сами измеряемые величины, а их функции, подобранные в соответствии с решаемой задачей. Например, если измеряемая величина изменяется очень сильно, на несколько порядков, удобно применять логарифмический (по осям откладываются логарифмы измеряемых величин) или полулогарифмический масштаб (логарифм откладывается только по одной из осей). С примером полулогарифмической шкалы Вы встретитесь в работе по снятию аудиограммы и частотной характеристики импеданса биологической ткани.
При пользовании функциональных масштабов на оси следует наносить двойную шкалу: одну – равномерную для откладываемой по оси функции (например, lg x), а другую – неравномерную для самой величины (но и на эту шкалу наносят, как обычно, “круглые” числа.

9. Оформление графиков. Готовый график, снабжается подписью, которая должна содержать точное описание того, что показывает график.
Ниже показан пример построения графика (к лаб. раб.№ 1).
Рис. 1
Зависимость чувствительности α весов от величины нагрузки P.
10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх =75 г : α 75 = 
11. На основании графика можно найти абсолютную погрешность в определении одной из величин, если известна абсолютная погрешность другой величины. Пусть график изображает зависимость y = f(x) и известно, что некоторое значение величины Х измерено с погрешностью Δх (точка Х0). Тогда
Рис. 2
Зависимость y=f(x)
на графике откладывают на соответствующей оси около значения Х0 величину ΔX в выбранном масштабе и по графику находит соответствующую ей величину отрезка ΔY (см. рис.). Найденное ΔY и будет представлять собой абсолютную погрешность в определении Y.
Гальванопластика — направление прикладной электрохимии, направленное на создание изделий путем электрохимического осаждения металлов и сплавов на различные носители формы (формообразующие элементы) в жидких средах.
Принцип формирования металлического осадка на поверхности модели, такой же как и при гальваническом нанесении покрытий, но в отличии от классической гальваники (гальваностегии) – толщина формируемых металлических осадков может достигать нескольких сантиметров.
В первой половине 20 века применение гальванопластики с целью получения технических изделий превратилось в полноценную промышленную технологию получения сложных и точных изделий.
При построении калибровочной прямой методом наименьших квадратов считается, что стандарты для калибровки известны с абсолютной правильностью или по крайней мере погрешности стандартов на одной из осей координат несущественны по сравнению с погрешностями откликов прибора на другой оси. Каждый отсчёт показаний шкалы прибора является единичным наблюдением, взятым из генеральной совокупности всех возможных отсчётов показаний шкалы прибора, при введении в него данного химического вещества. Такая ситуация изображена на рисунке:
Небольшие кривые нормального распределения, начерченные на графике, представляют генеральную совокупность всех возможных сигналов прибора при измерении стандартов 0,300, 0,600, 0,900 мг/дм3. Точка А, наблюдаемая в процессе калибровки, расположена близко к центру этого распределения (в пределах ±2σ, обозначенных штрихами). В данной ситуации точка А, представляющая значение оптической плотности стандарта 0,300 мг/л, находится близко к генеральному среднему. Но при измерении необходимо, чтобы калибровочная прямая проходила не через точку А, а точно через центр распределения, который обозначен стрелкой, для чего мы пользовались методом наименьших квадратов. Для минимизации погрешности относительно оси У при составлении градуировочного графика используются средние значения трёх параллельных измерений каждого стандартного образца (см. «Статистическая обработка данных титриметрического анализа»), поэтому эти расчёты мы рассматривать не будем. Мы рассмотрим расчёт доверительных интервалов для коэффициента bи полученной в ходе измерения концентрации вещества в исследуемом растворе xk.
При определении недостоверностей при работе методом градуировочного графика первая необходимая величина, надлежащая определению, — дисперсия, обусловленная рассеянием точек относительно линии регрессии, выраженная уравнением:
Далее определяется дисперсия коэффициента регрессии или стандартного отклонения b:
Доверительные интервалы задаются обычным способом по таблице коэффициентов Стьюдента при доверительной вероятности 95%:
за тем исключением, что число степеней свободы k = n-2, где n– количество стандартов для градуировки.
На практике линию регрессии (линию градуировочного графика) используются, чтобы получить оценку некоторой величины (в нашем случае концентрации железа II) xk измеряемого вещества, которая вызывает наблюдаемый отклик прибора yk (поглощение раствора). Дисперсия определяемой величины xk при наблюдении mоткликов (m – количество параллельных измерений) выражается уравнением:
s 2 xk = (s 2 x,y / b 2 ) * [(1/m + 1/n) + (у¯k — у¯) 2 / b 2 ∑U 2 )] , для этого выражения стоит отметить следующее:
а) xk – характеристика вещества, ответственного за отклик прибора. В нашем случае xk – концентрация железа II, соответствующая наблюдаемому поглощению раствора yk.
б) yk(∑yk/m) – средний отклик прибора, полученный для ряда из mизмерений. Часто проводят только одно измерение и поэтому m=1.
в) Величины s 2 x,y, b, n, у¯ и ∑U 2 связаны с данными при калибровке прибора и имеют те же самые значения, что мы получили при уточнении градуировочного графика методом наименьшик квадратов.
Стоит обратить особое внимание, что s 2 xkвозрастает по мере удаления yk от у¯. Из математического выражения следует, что недостоверность любой оценки регрессии меньше всего вероятна вблизи центра калибровочных данных и поэтому экстраполяция представляет собой очень ненадёжный метод и при измерениях не используется. Разбавление исследуемого раствора подбирается таким образом, чтобы отклик прибора при измерении попадал как можно ближе к центру градуировочной прямой.
Доверительные интервалы для определяемой величины xk выражаются следующим образом:
Продолжим расчёт определения железа IIпо градуировочному графику, построенному по 6 точкам (n=6) с уравнением регрессии у = 0,002245098 + 10914,70588х (см. Применение регрессионного анализа для построения градуировочного графика при фотометрическом анализе).
Допустим, что а) при единичном (m=1) измерении исследуемого раствора получено поглощение равное 0,527, б) при пяти (m=5) повторных измерениях среднее поглощение равно 0,527.
1) Вычисляем дисперсию относительно линии регрессии:
s 2 x,y = (∑V 2 – b 2 ∑U 2 )/(n-2) = (0,40539683 – (10914,70588^2)*0,0000000034)/(6-2) = 0,0000880245098
2) Вычисляем стандартное отклонение b:
s 2 bx,y = s 2 x,y / ∑U 2 = 0,0000880245098 / 0,0000000034 = 25889,561707
3) Рассчитываем доверительный интервал для коэффициента b:
При доверительной вероятности 95% для φ=n-2=4 коэффициент tα,φ принимает значение 2,776 (см. таблицу коэффициентов Стьюдента).
b = (10914,70588 ± 446,66) ≈ (10915 ± 447)
4) Рассчитаем по уравнению регрессии, выразив его через x, концентрацию железа IIxkпо поглощению 0,527, полученному в ходе измерения исследуемого раствора:
x = -0,000000205695 + 0,00009161950957y
xk= -0,000000205695 + 0,00009161950957*0,527 = 0,00004807778 ≈ 0,000048 моль/л
5) Стандартное отклонение оценки регрессии s 2 xk для случаев а) m=1 и б) m=5:
а) s 2 xk = (s 2 x,y / b 2 ) * [(1/m + 1/n) + (у¯k — у¯) 2 / b 2 ∑U 2 )] = (0,0000880245098 / 10914,70588^2)*[(1/1 + 1/6) + (0,527 — 0,438833)^2 / (10914,70588^2 * 0,0000000034] = 0,000000000000876218
sxk = √s 2 xk = √0,000000000000876218 = 0,000000936065
б) s 2 xk = (0,0000880245098 / 10914,70588^2)*[(1/5 + 1/6) + (0,527 — 0,438833)^2 / (10914,70588^2 * 0,0000000034] = 0,0000000000002851065
sxk = √0,0000000000002851065 = 0,0000005339536
6) Рассчитываем доверительный интервал для xk:
При доверительной вероятности 95% для φ=n-2=4 коэффициент tα,φ принимает значение 2,776 (см. таблицу коэффициентов Стьюдента).
а) ДИ = ε α,t =±tα, φ * sxk = 2,776* 0,000000936065 = 0,000002598
xk = (0,00004807778 ± 0,000002598) ≈ (0,0000481 ± 0,0000026) моль/л
б) ДИ = ε α,t = ±tα, φ * sxk = 2,776*0,0000005339536 = 0,0000014823
xk = (0,00004807778 ± 0,0000014823) ≈ (0,0000481 ± 0,0000015) моль/л
7) Рассчитываем относительную ошибку определения:
а) εотн = (ε α,t / хk)*100 = 0,0000026*100/0,0000481 = 5,4%
б) εотн = (ε α,t / хk)*100 = 0,0000015*100/0,0000481 = 3,1%
Расчёты относительных ошибок измерений показывают, что использование метода наименьших квадратов не может заменить правильность самих калибровочных данных. Метод наименьших квадратов не должен применяться только для расчётов коэффициентов a и b, но должны рассчитываться также недостоверности относительно линии регрессии по алгоритму, указанному выше. При исключении расчётов недостоверностей статистический метод используется неправильно, и химик-аналитик обманывает себя и других, приводя в своих результатах слишком много значащих цифр.
Образец автоматических расчётов недостоверностей градуировочного графика, построенного по 6 точкам, можно скачать здесь .
1. Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение. Теория и практика аналитической химии. – М.: «Химия», 1978. – 816 с.
2. А.П.Крешков. Основы аналитической химии. Книга вторая. — М.: «Химия», 1971.- 456 с.
И снова о погрешностях
Окончание. См. № 15/07
Д.А.ИВАШКИНА,
лицей г. Троицка, Московская обл.
aivashkin@mail.ru
И снова о погрешностях
4. Учёт случайных погрешностей при
прямых измерениях
Если, проведя одно и то же измерение
несколько раз, вы видите, что результат остаётся
одним и тем же, то случайные погрешности
эксперимента малы, их не следует учитывать. Но
если при повторении измерения получаются разные
значения, то следует взять среднее значение из
серии измерений:
где n – число измерений. Как
узнать, какова погрешность результата? Логично, и
ученики сами обычно предлагают это, определить
среднее отклонение результата от среднего
значения. Полученная величина носит название средней
арифметической ошибки: Она показывает, на сколько в
среднем каждое измеренное значение отклоняется
от среднего значения. Но эта величина слабо
зависит от количества проведённых измерений. В
чём же тогда смысл многократных измерений?
Для среднеквадратичной погрешности,
которая определяется немного сложнее:
есть простое правило: средняя
квадратичная погрешность среднего
арифметического равна средней квадратичной
погрешности отдельного результата, делённой на
корень квадратный из числа измерений: Из формулы ясно,
что с увеличением числа измерений случайная
погрешность среднего значения уменьшается.
Поэтому необходимо проводить столько измерений,
чтобы случайная погрешность стала меньше
значения систематической погрешности данного
измерения.
К сожалению, в лабораторных работах и
при любых других экспериментах в школе провести
достаточное количество измерений невозможно в
силу нехватки времени. Как поступать, может
решить сам учитель. На мой взгляд, для нахождения
средней арифметической погрешности среднего
значения можно использовать формулу,
аналогичную формуле для средней квадратичной
ошибки:
Хотя эта формула и неверна, она
помогает понять смысл проведения большого числа
измерений. Использоваться же она будет всего в
нескольких работах, и, следовательно, нет нужды
специально обучать нахождению погрешности
среднего значения. Зато, получив в этих работах
случайную погрешность меньше погрешности
систематической, ученик запомнит, что каждое
измерение следует производить несколько раз при
малейшем подозрении, что в данном эксперименте
имеется случайная погрешность. Как правило, уже
при пяти измерениях достигается необходимая
малость случайной погрешности по сравнению с
систематической.
5. Определение погрешности
результата косвенных измерений
К определению погрешности результата
косвенных измерений учащиеся готовы, на мой
взгляд, уже к 8-му классу. В зависимости от уровня
класса впервые метод границ [1, 12] можно
применить или в работе по сравнению количеств
теплоты при смешивании воды, или при нахождении
сопротивления проводника. Поясню на примерах.
-
Допустим, при нагревании холодной
воды в процессе смешивания мы имеем следующие
результаты измерений:
– температура холодной воды t1
= (16,0 ± 1,5) °С;
– температура смеси t = (43,0 ± 1,5) °С;
– объём холодной воды V1 = (80
± 2) мл = (80 ± 2) • 10–6 м3.
Получаем количество теплоты,
полученное холодной водой:
Q = 4190 Дж/(кг • °С) • 1000 кг/м3
• 80 • 10–6 м3 (43 – 16) °С = 9050,4 Дж.
(1)
Возникает вопрос: а какова погрешность
полученного значения? Другими словами, на
сколько мы можем ошибиться, если точные значения
не равны измеренным, а лежат где-то в интервале,
даваемом погрешностью? Например, начальная
температура воды может быть равна 16,5 °С, 17,0 °С и
т.д. Тогда вычисленное количество теплоты будет
меньше. Логично посмотреть, на сколько мы можем
ошибиться по максимуму. Максимальное количество
теплоты получится, если взять для всех
сомножителей максимальные значения, т.е. верхние
границы интервалов значений с погрешностью, для
уменьшаемого взять верхнюю границу значения, а
для вычитаемого – нижнюю:
Qв = 4190 Дж/(кг • °С) • 1000
кг/м3 • 82 • 10–6 м3 (44,5 – 14,5)°С = 10 307,4 Дж.
Аналогично вычисляем нижнюю границу
значения количества теплоты:
Qн = 4190 Дж/(кг • °С) • 1000
кг/м3 • 78 • 10–6 м3 (41,5 – 17,5) °С = 7843,68
Дж.
В данных пределах и лежит искомое
значение. Чтобы сравнивать методом интервалов
это значение с количеством теплоты, отданным
горячей водой, надо округлить значения верхней и
нижней границ. Лучше это сделать, оценив
абсолютную погрешность найденного значения
количества теплоты.
Рис. 2
Из рис. 2 видно, что
Найденное выше значение (1) близко к (3),
поэтому его не стоит находить ещё раз. А вот для
погрешности найдём с помощью (2):
(две
значащие цифры, т.к. первая «1»). Поэтому
количество теплоты, полученное холодной водой,
можно округлить: Qполуч = 9000 Дж ±
1200 Дж (т.е. между 7800 Дж и 10 200 Дж). Если количество
теплоты, отданное горячей водой, лежит между 8500
Дж и 11 500 Дж (Qотдан = 10 000 Дж ± 1500 Дж), то
можно видеть, что эти количества теплоты
совпадают в пределах погрешности эксперимента
(рис. 3).
Рис.3
-
Определение сопротивления резистора.
Пусть измеренные значения напряжения и силы тока
следующие:
– U = 2,60 В ± 0,15 В (инструментальная
погрешность 0,15 В; погрешность отсчёта может быть
взята равной 0,05 В, т.е. в 3 раза меньше
инструментальной, поэтому ею можно пренебречь);
– I = 1,2 А ± 0,1 А (инструментальная
погрешность 0,05 А, погрешность отсчёта 0,05 А).
Тогда для сопротивления получаем:
Но на самом резисторе написано: «2 ± 0,1 ». Получается, что
мы неверно определили сопротивление? Рассчитаем
погрешность нашего определения значения
сопротивления:
Uв = 2,75 В; Uн = 2,45 В; Iв
= 1,3 А, Iн = 1,1 А;
Полученное экспериментально значение
сопротивления R = (2,2 ± 0,3) Ом совпадает в
пределах погрешности со значением R = (2,0 ± 0,1)
Ом, указанным на резисторе.
С помощью метода границ можно вывести
и формулы для погрешности при обобщении темы
«Определение погрешности косвенных измерений»,
но уже в 9-м классе.
Определение погрешности разности. Пусть
А = В – С. Рассчитаем погрешность А в
общем виде:
Ав = Вв – Сн
= (В + В)
– (С – С)
= (В – С) + (В
+ С);
Ан = Вн – Св
= (В – В)
– (С + С)
= (В – С) – (В
+ С);
Полученное очень важно: в некоторых
работах в формулах для вычисления результата
встречается разность двух близких по значению
величин, что приводит к большой относительной
погрешности результата.
-
В cтарой работе «Определение модуля
Юнга резины» [11] удлинение резинового жгута
находилось как разность его результирующей и
начальной длин. Если условия опыта таковы, что
эта разность мала, например, составляет 1,5 см, то
относительная погрешность определения разности(погрешность
отсчёта взята гораздо меньше инструментальной
погрешности). Ясно, что такое измерение
использовать для определения модуля Юнга
нежелательно, – может получиться погрешность
больше 100%. Лучше увеличить нагрузку на жгут.
Аналогичная проблема возникает в работе
«Измерение ЭДС и внутреннего сопротивления
источника» [2] (одно сопротивление должно быть в
несколько раз больше другого) и др.
Определение погрешности частного
двух величин. Пусть Рассчитаем погрешность в общем виде:
Такую формулу трудно запоминать.
Поэтому найдём относительную погрешность
величины А:
Итак, относительная погрешность
частного равна сумме относительных погрешностей
величин, входящих в него. Такая же формула
получается и для относительной погрешности
произведения.
Важным я считаю не сам процесс расчёта
погрешности. Эти формулы дают мощный инструмент
для оценки обоснованности проведения
эксперимента. При их использовании легко
объяснить, при измерении какой из величин
следует увеличить точность, чтобы получить
лучший результат.
Рассмотрим формулу для нахождения
модуля Юнга:
Если воспользоваться для расчёта погрешности
результата методом границ, то неясным останется,
какая из величин в формуле вносит наибольшую
погрешность.
Для нахождения относительной
погрешности результата лучше воспользоваться
формулой:
При подстановке значений оказывается,
что слагаемое
даёт максимальный вклад в сумму, а остальные
слагаемые в несколько раз меньше, так что ими
можно пренебречь. Если l – l0 будет
невелико, то значение относительной погрешности
окажется очень большим, порой выше 100%. Какой
вывод сделают в таком случае ученики?
Такая ситуация – пример того, как
применение упрощённого способа вычисления
погрешностей может привести к большим ошибкам.
Конечно же, этот эксперимент совершенно
обоснован, с помощью него можно найти модуль
Юнга. Только следует выбрать те измерения, где l
– l0 достаточно велико, и не забыть
пренебречь малыми слагаемыми при расчёте
погрешности.
6. Определение коэффициента
прямой пропорциональности
В лабораторных работах нередко
встречается ситуация, когда необходимо по
графику определить коэффициент
пропорциональности в зависимости одной величины
от другой. И здесь в учебниках встречаются две
ситуации.
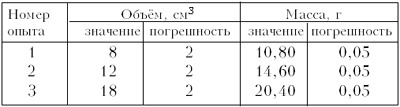
В работе «Определение модуля Юнга» [13]
после нахождения модуля Юнга для измерений с
тремя различными нагрузками учащимся
предлагается найти среднее арифметическое трёх
полученных значений. Такой подход ошибочен, т.к.
каждое значение получено с различными
систематическими погрешностями, т.е. с разной
степенью точности. Нельзя суммировать эти
значения «с одинаковым весом». При подобных
вычислениях в теории ошибок находится сумма этих
значений с разными коэффициентами.
Далее, в работе «Измерение жёсткости
пружины» [7] в аналогичной ситуации совершенно
справедливо отмечено, что, поскольку жёсткость
пружины в каждом из опытов получена при разных
условиях, среднее арифметическое этих значений
находить нельзя. И предлагается найти среднее
значение коэффициента жёсткости по графику как
коэффициент пропорциональности. Однако,
поскольку учащиеся не могут найти погрешность
найденного таким образом коэффициента
пропорциональности, предлагается взять в
качестве этой погрешности погрешность
наихудшего результата. Я считаю, что такой подход
не оправдан. Зачем брать погрешность самого
ненадёжного результата, если сам способ
нахождения коэффициента жёсткости из графика
применяется для того, чтобы определить этот
коэффициент наиболее точно? Думаю, авторы просто
не хотели заострять внимание на этом вопросе.
На мой взгляд, для определения
коэффициента пропорциональности по графику
можно предложить несколько вариантов.
Вариант 1. Самый простой, а потому
пригодный для младших классов. Отмечаем на
графике экспериментальные значения с указанием
погрешности. Обращаем внимание учащихся на то,
что если бы мы не нанесли погрешности на графики,
то провести прямую было бы затруднительно. В 7-м
классе достаточно просто отметить тот факт, что
зависимость между двумя величинами прямо
пропорциональна. Но если всё-таки необходимо
найти значение коэффициента пропорциональности,
можно обойтись без расчёта погрешности, отметив
только, что этот способ (многократные измерения
при различных условиях и построение графика)
используется именно для того, чтобы уменьшить
погрешность результата.
Вариант 2. Чертим прямую, находим
экспериментальную точку, которая лежит ближе
всего к прямой, и именно эту точку и считаем самой
точной. Остаётся вычислить результат для неё по
обычным формулам, рассчитав также и погрешность.
Вариант 3. Самый логичный. Пробуем
провести через точки вместе с их погрешностями
две прямые: с наибольшим и с наименьшим наклоном.
Значения коэффициентов для них и будут верхней и
нижней границами для результата. Зная границы,
рассчитываем среднее значение коэффициента и
погрешность. Данная погрешность неявно будет
содержать в себе как систематическую
погрешность экспериментально измеренных
величин, так и случайную погрешность определения
среднего, но уже с учётом точности каждого
результата. Этот вариант годится для
использования в экспериментах, когда
коэффициент должен быть оценён достаточно точно.
Но он достаточно сложен, поэтому не стоит его
использовать во всех случаях.
Вариант 4. Использование
встроенных программ в калькуляторах или готовых
компьютерных программ для вычисления
коэффициентов по методу наименьших квадратов.
Этот способ пригоден для практикума в старших
классах и/или в классах физматпрофиля. К
сожалению, в такие программы, как правило,
встроен метод наименьших квадратов, не
учитывающий погрешностей экспериментальных
точек. Применение имеет смысл в случаях, когда
погрешности всех точек практически одинаковы
или когда доминирующей является случайная
погрешность. Она и будет учтена.
Какой из этих вариантов выбрать, может
решать сам учитель. К счастью, таких работ
довольно мало. Продемонстрируем все эти варианты
на примере.
-
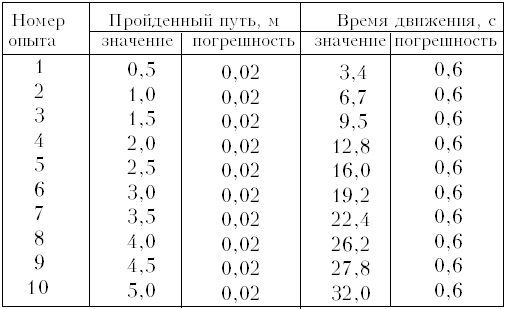
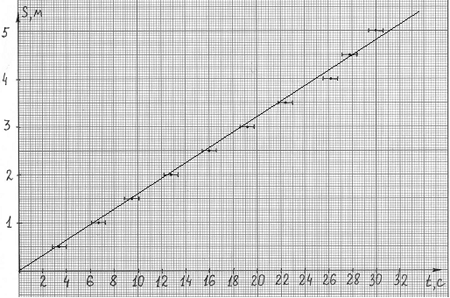
Возьмём данные эксперимента по
зависимости пути от времени равномерного
движения (машинка из конструктора с
электрическим приводом):
Действуя так, как описано в варианте 1,
строим график (рис. 4).
Рис. 4
Так как точек на графике много, можно с
уверенностью утверждать, что 8-я и 10-я точки
являются «выбросами», т.е. измерены небрежно.
Учитывая погрешность эксперимента, можно
провести прямую практически единственным
способом: соответствующая скорость 0,16 м/с. Если
воспользоваться методом наименьших квадратов
(например, встроенной функцией ЛИНЕЙН в
программе MicrosoftExcel), то для коэффициента мы
получим значение 0,158 ± 0,002 м/с (вариант 4).
Для варианта 2 подходит 3-я точка.
Скорость, вычисленная по данным для этой точки,
0,158 м/с. Рассчитаем погрешность: Так как относительная
погрешность пути мала по сравнению с
относительной погрешностью времени,
пренебрегаем ею. Абсолютная погрешность
результата: 0,063
• 0,158 = 0,010 м/с. То есть скорость, вычисленная в
варианте 2: (0,158 ± 0,010) м/с.
Из приведённого примера видно, что
значения коэффициента пропорциональности
получаются очень близкими. В этом примере
погрешности отдельных измерений были достаточно
малы, а точек, наоборот, было много. Рассмотрим
пример, когда погрешности, напротив, велики, а
количество опытов в силу объективных причин
мало.
-
Найдём плотности пластмассы путём
измерения массы и объёмов тел.
В случае варианта 1 прямую проводим
так, чтобы количество точек над и под прямой было
одинаково (рис. 5), т.е. в данном случае – одна
сверху, одна снизу (прямая 1). Плотность в
этом случае равна 1,23 г/см3.
Рис. 5
В случае варианта 2 пригодна 2-я точка.
Для неё значение плотности (1,2 ± 0,2) г/см3.
Вариант 3: проведём прямые 2 и 3.
Для прямой 2 коэффициент пропорциональности
1,09 г/см3 является нижней границей
искомого значения плотности, а для прямой 3
(1,27 г/см3) – верхней. Полусумма этих
значений есть значение плотности (1,18 г/см3),
а полуразность – значение погрешности (0,09 г/см3).
Вариант 4 в данном случае менее
пригоден, т.к. не учитывает больших значений
погрешностей при измерении объёма с помощью
мерного цилиндра, но и в этом варианте плотность
(1,18 ± 0,05) г/см3.
Следует заметить, что в двух последних
примерах на графиках были обозначены только
погрешности вдоль горизонтальной оси, т.к.
погрешности значений второй переменной были
очень малы.
Послесловие
Научиться обрабатывать результаты
экспериментов учащиеся могут, лишь обрабатывая
результаты экспериментов. Это означает, что
помимо стандартного набора лабораторных работ
необходимо проводить много фронтальных и
демонстрационных экспериментов с обработкой
результатов. Это большая работа, и я хочу
пожелать успехов всем учителям, кто вступит на
этот путь или уже стоит на нём.
Литература
1. Анофрикова С.В., Стефанова Г.П.
Практическая методика преподавания физики.
Часть первая. – Астрахань: Издательство
Астраханского ГПИ, 1995.
2. Физика: Под ред. А.А.Пинского: Учебник
для 10 кл. школ и классов с угл. изучением физики. –
М.: Просвещение, 2002.
3. Попова О.Н. Обучение учащихся
выявлению устойчивых связей и отношений между
физическими величинами: Методическое пособие
для учителей физики. – Элиста: Элистинский лицей,
1998.
4. Анофрикова С.В. Азбука
учительской деятельности, иллюстрированная
примерами деятельности учителя физики. Ч. 1.
Разработка уроков. – М.: МПГУ, 2001.
5. Пёрышкин А.В. Физика-8. – М.:
Дрофа, 2004.
6. Громов С.В., Родина Н.А. Физика-8.
– М.: Просвещение, 2000.
7. Кикоин И.К., Кикоин А.К. Физика-10.
Механика. – М.: Просвещение, 2001.
8. Фронтальные лабораторные занятия по
физике в 7–11 классах общеобразовательных
учреждений. Книга для учителя: Под ред. В.А.Бурова,
Г.Г.Никифорова. – М.: Просвещение, Учебная
литература, 1996.
9. Зайдель А.Н. Элементарные оценки
ошибок измерений. – Л.: Наука, 1967.
10. Хорозов С.А. Работа над
ошибками: В кн. «Энциклопедия для детей», т. 16
«Физика», ч. 1 «Биография физики. Путешествие в
глубь материи. Механистическая картина мира». –
М.: Аванта+, 2000.
11. Мякишев Г.Я., Буховцев Б.Б., Сотский
Н.Н. Физика-10. – М.: Просвещение, 2004.
12. Кирик Л.А. Физика-9: Методические
материалы. – М.: Илекса, 2003.
13. Шахмаев Н.М., Шахмаев С.Н., Шодиев
Д.Ш. Физика-10. – М.: Просвещение, 1994.
















![[IMG]](http://corum.mephist.ru/tex/images/b7cd22a4bb1c3d8abaa342cd2ada4701.gif) (
(![[IMG]](http://corum.mephist.ru/tex/images/48291f83278dbe78bb6d25c83d42b779.gif) ) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале ![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) , а в 30% — не будут.
, а в 30% — не будут.![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/fe09543b974240017f246c36f0e20bad.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/a5cada5c2d1ccb4b76fbda0fb521adb3.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b4bebab07d35bbb43ec16714f5ed87c8.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/2e68c7fa8bf3791b61039377fa19d559.gif) но
но ![[IMG]](http://corum.mephist.ru/tex/images/f9c474b6e9e0acb125b588c2978f94e4.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/42a0f383586370bf8d25ece709fbb3e8.gif) , поскольку тут 2 значащие цифры — 2 и 0 после двойки.
, поскольку тут 2 значащие цифры — 2 и 0 после двойки. ![[IMG]](http://corum.mephist.ru/tex/images/d5d51f35586a0011459580a47c329c1c.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/bf7e5189fad7ab2880e4fc7c5411fea9.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/9182580f66fbbe10919734c8448a2b0e.gif)
![[IMG]](http://corum.mephist.ru/tex/images/74ccc55c5f11b678eee65f6d66b9a60d.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/60673e2250d177e624ad95b43064ca5e.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/af619a318dbcab2d7ff6c6654f907177.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b928ec2d5d3d00612d6b75b0024e52e6.gif)
![[IMG]](http://corum.mephist.ru/tex/images/5e73d4508bfbc87a12895031f6919e08.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/e51638f79ed91c6edb4a330fbfeb683c.gif) мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица.
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица. ![[IMG]](http://corum.mephist.ru/tex/images/03ffd1a1b9f618fd926a47a5ca0fc293.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/96072c008b0f5d6a865359f39cd1e082.gif) мм. Здесь лишний знак в результате. Правильно будет
мм. Здесь лишний знак в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. ![[IMG]](http://corum.mephist.ru/tex/images/2291014f831b0fd0257924da54867d23.gif) мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/27b6e5ddc95fcf2627e37957689fa579.gif) У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:![[IMG]](http://corum.mephist.ru/tex/images/cf5c3f00f8d2fe027241a59955d5ceae.gif)
![[IMG]](http://corum.mephist.ru/tex/images/8fbdcb7dc81fe147175bc997b0fb2119.gif) означает частную производную f по x. Подробнее про частные производные здесь.
означает частную производную f по x. Подробнее про частные производные здесь.![[IMG]](http://corum.mephist.ru/tex/images/a0311888c35b344c57ef62341814562b.gif) . Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) , которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:![[IMG]](http://corum.mephist.ru/tex/images/c7f83b4f19066a525f2969ce1c8ce372.gif)
![[IMG]](http://corum.mephist.ru/tex/images/4c795de483c9c9897980b7ba74c847fc.gif) означает среднее по всем
означает среднее по всем ![[IMG]](http://corum.mephist.ru/tex/images/fac074461d1491da3757d3b266ebf89c.gif) .
. ![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) , который зависит от выбранной вами доверительной вероятности
, который зависит от выбранной вами доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/ceb95147a8605f55cd8513ecd26cc1fd.gif) .
. 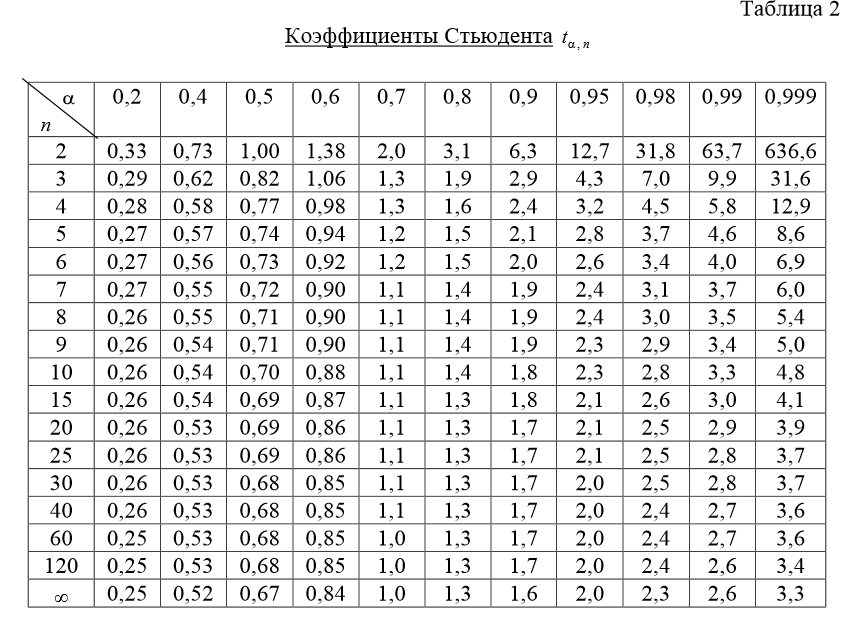
![[IMG]](http://corum.mephist.ru/tex/images/bb6c84165e61208b5b7b94e889085f7f.gif)
![[IMG]](http://corum.mephist.ru/tex/images/80a15ae9b42d82e8676bae47fcab70b3.gif) доверительная вероятность должна быть одинаковой.
доверительная вероятность должна быть одинаковой. ![[IMG]](http://corum.mephist.ru/tex/images/b853078084cb450336d8305ee3ff0051.gif)
![[IMG]](http://corum.mephist.ru/tex/images/c391ad2e2574b7c9ffb7f64916b97dc2.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/e3f04bbaaa490a4d496e19c05c63f31e.gif) совпадают.
совпадают. 
![[IMG]](http://corum.mephist.ru/tex/images/59b6fc687986871e08a4def089688bbf.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/a5f06e8811bf82a53ff629bd97e8417e.gif) — величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
— величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.![[IMG]](http://corum.mephist.ru/tex/images/fd7f8eb5a1972f4158afd23480837110.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/8f29cb2c179bfc115aa33e7730d3954d.gif) — наибольшее значение сопротивления магазина, а
— наибольшее значение сопротивления магазина, а ![[IMG]](http://corum.mephist.ru/tex/images/7d47b66519d27f5821540aa071c3d561.gif) — номинальное значение включённого сопротивления.
— номинальное значение включённого сопротивления. ![[IMG]](http://corum.mephist.ru/tex/images/e1b00eb5241498c481dfb7468c96e465.gif)
![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?

![[IMG]](http://corum.mephist.ru/tex/images/795e28a5ddba8232883f37576bbf11cf.gif) . Это, разве, не полностью аналогичный случай к правильному варианту записи?
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
![[IMG]](http://corum.mephist.ru/tex/images/e7493bf11a89e41c4c62b4e8aee498a5.gif) — правильно?
— правильно?
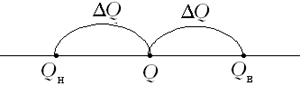
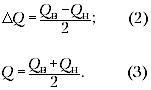
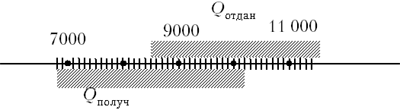
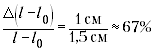 (погрешность
(погрешность